위성 SAR 기만 재밍을 위한 RLSE 기반 SAR 파라미터 추정 기법

I. 서 론

합성 개구면 레이다(SAR, synthetic aperture radar)는 전자기파를 통해 획득한 지표면 및 표적에 대한 정보를 고해상도 영상으로 변환해 주는 레이다 시스템이다^[1]. 광학 영상과는 달리 SAR는 주야 및 기상에 무관하게 영상을 획득할 수 있다는 장점으로 인해 군수 및 민수 분야에서 활발히 사용되고 있다^[2]~[4]. 특히 위성 SAR는 그 특성상 지구 주위를 공전하며 넓은 지역을 관측하기 때문에, 감시정찰과 표적 탐지 및 식별 등 군사적 용도로 많이 활용되고 있다. 이에 따라 더욱 강건한 우주 기반 감시정찰 시스템을 구축하기 위해 수많은 SAR 위성들이 발사되고 있으며, 효과적인 임무 수행을 위해 다양한 SAR 기술들 또한 개발되고 있다^[5]~[7].

이와 동시에 적성 SAR의 감시정찰에 대항하여 아군의 주요 자산 및 정보를 보호하기 위해, SAR 재밍(jamming) 기법 또한 많은 관심을 받고 있다. SAR 재밍 기법은 그 목적에 따라 잡음 재밍(noise jamming)과 기만 재밍(deceptive jamming)으로 구분되며, 그중 기만 재밍은 적성 SAR 영상에 실제로 존재하지 않는 허위 표적에 대한 정보가 형성되도록 하는 기법이다^[8],[9]. SAR 영상에 허위 표적을 형성하기 위해 재머(jammer)는 SAR의 신호 특성을 반영한 기만 신호를 방사하며, 이러한 특징으로 인해 기만 재밍은 적이 재밍 유무를 판단하기 어렵게 만든다. 또한 기만 재밍은 잡음 재밍과 같이 영상의 전체 또는 일부를 전력이 큰 잡음으로 덮어버리는 것이 아니기 때문에, 적은 전력을 소모한다는 장점도 가진다^[10],[11].

기존의 기만 재밍 기법들은 SAR의 신호 특성을 반영한 기만 신호를 방사하기 위해, 수신된 SAR 신호 자체를 활용하여 기만 재밍을 수행하는 데 초점을 맞추고 있다. 그중 직접 재송신 기반 기만 재밍 기법은 수신된 SAR 신호에 허위 표적에 대한 정보를 결합하고, 특정 시간을 지연시킨 후 SAR를 향해 방사한다^[12]~[14]. 하지만 이 기법은 하나의 허위 점 표적만을 형성할 수 있다. 이에 따라 여러 개의 점 표적으로 구성된 허위 표적을 형성하기 위해, 변조-재송신 기반 기만 재밍 기법이 주로 연구되고 있다^[15]~[20]. 이 기법은 주파수 축에서 템플릿(template)으로 구성된 허위 표적에 대한 정보와 수신된 SAR 신호를 결합하여 SAR를 향해 방사한다. 그러나 두 기법 모두 SAR 신호를 수신하고, 특정 시간 뒤에 기만 신호를 방사함에 따라 SAR의 관심 영역 내에서 거리축을 기준으로 재머의 뒤쪽 위치에만 허위 표적을 형성할 수 있다. 이는 허위 표적 위치 설정 측면에서 명백한 한계점으로 작용한다. 이를 극복하기 위해 기만 신호를 사전에 생성해 놓고, 재머에 SAR 신호가 수신되기 전에 기만 신호를 방사하는 새로운 기만 재밍 기법을 고려해볼 수 있다.

이에 본 논문은 상기에서 언급한 기만 재밍 기법에 대한 연구의 일환으로서, 현재 수신된 SAR 신호로부터 다음 SAR 신호의 송신 시점과 중심 주파수를 추정하는 기법을 제안한다. 제안하는 기법은 크게 펄스 압축을 통한 신호의 도착 시간과 위상을 측정하는 단계와 측정된 도착 시간과 위상, 그리고 RLSE(recursive least square estimation)를 통해 다음 SAR 신호의 송신 시점과 중심 주파수를 추정하는 단계로 구분된다. 이 기법은 다음 신호의 송신 시점을 샘플링 간격 미만의 오차로, 중심 주파수를 0.1 Hz 미만의 오차로 정확하게 추정할 수 있다. 추정된 중심 주파수는 사전에 생성된 기만 신호를 RF(radio frequency) 대역으로 변환하는 데 사용되며, 추정된 신호의 송신 시점은 이 기만 신호의 방사 시점을 결정하기 위해 사용된다.

본 논문의 구성은 다음과 같다. 먼저 Ⅱ장에서 제안하는 기법의 연구 배경에 대하여 기술한다. 다음으로 Ⅲ장에서 제안하는 SAR 파라미터 추정 기법과 추정된 파라미터를 통해 허위 표적 위치 설정의 한계점을 극복할 수 있는 기만 재밍 기법을 설명한다. 그 후 Ⅳ장에서 모의실험을 통해 제안하는 추정 기법의 성능을 분석하며, 마지막으로 Ⅴ장에서 본 논문의 결론을 내린다.

Ⅱ. 연구 배경

2-1 직접 재송신 기반 기만 재밍 기법

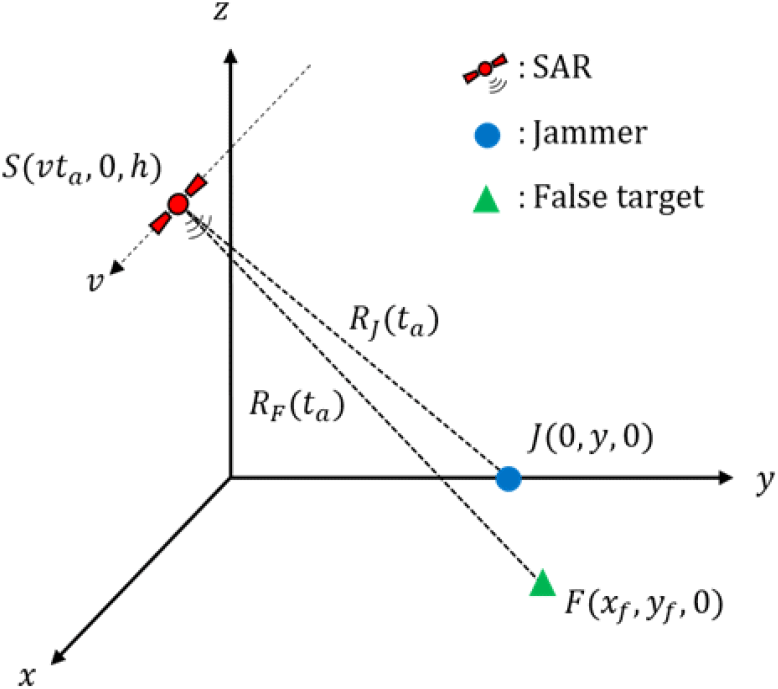
그림 1과 같이 방위 시간 t_a에 따라 x축과 평행하게 일정 속도 v로 이동하고 있는 SAR의 위치 좌표를 S(vt_a,0,h), 고정된 재머의 위치 좌표를 J(0,y,0), 허위 표적의 위치 좌표를 F(x_f, y_f, 0)라고 할 때, SAR와 재머, 허위 표적 간의 거리는 식 (1)과 같이 나타낼 수 있다.

$$\begin{array}{c}{R}_J\left(t_a\right)=\left|\text{SJ}\right|=\sqrt{{\left(v{t}_a\right)}^2+y^2+h^2},\\ R_F\left(t_a\right)=\left|\text{SF}\right|=\sqrt{{\left(v{t}_a-x_f\right)}^2+y_f^2+h^2}.\end{array}$$

(1)

그림 1. | Fig. 1. 위성 SAR 기만 재밍 기하 구조 | Geometry of deceptive SAR jamming.

Download Original Figure

여기서 R_J(t_a)와 R_F(t_a)는 각각 t_a에 따라 변화하는 SAR와 재머 간의 거리와 SAR와 허위 표적 간의 거리를 나타낸다. 만약 조건 $\sqrt{y^2+h^2}\gg v{t}_a$, $\sqrt{y^2+h^2}\gg v{t}_a-x_f$, $\sqrt{y^2+h^2}\gg y_f-y$를 만족한다면, SAR와 재머, SAR와 허위 표적 간의 거리 차 ΔR(t_a)는 식 (2)와 같이 근사하여 나타낼 수 있다.

$$\text{Δ}R\left(t_a\right)=R_F\left(t_a\right)-R_J\left(t_a\right)\approx \sqrt{x_f^2+{\left(y_f-y\right)}^2}.$$

(2)

상기 유도 과정을 토대로 직접 재송신 기반 기만 재밍의 기본적인 수행 과정은 재머에서 SAR 신호를 수신하고, 수신된 신호에 (2×ΔR(t_a))/c만큼의 시간 지연을 적용한 후(여기서 c는 빛의 속도), 허위 표적에 대한 정보를 결합하여 SAR를 향해 방사한다^[12]~[14]. 이러한 수행 과정에 의해 SAR 영상에서의 좌표 F(x_f,y_f, 0)에는 단일 점 표적 하나가 형성된다.

하지만 근사를 통해 허위 표적을 생성할 경우, 근사 조건을 만족하지 않으면 허위 표적의 위치와 해상도 등에서 오차가 발생하게 된다. 이 때문에 일반적으로는 아군의 정찰 시스템으로부터 SAR의 궤도 정보를 제공받았다고 가정하고, 이를 활용하여 기만 재밍을 수행한다. 결과적으로 직접 재송신 기반 기만 재밍 기법의 핵심은 허위 표적 위치 좌표에서 반사된 SAR 신호가 SAR에 수신되는 시점에 맞춰 기만 신호를 방사함으로써, 해당 좌표에 허위 표적을 형성하는 것이다.

Ⅲ. 제안하는 SAR 파라미터 추정 기법

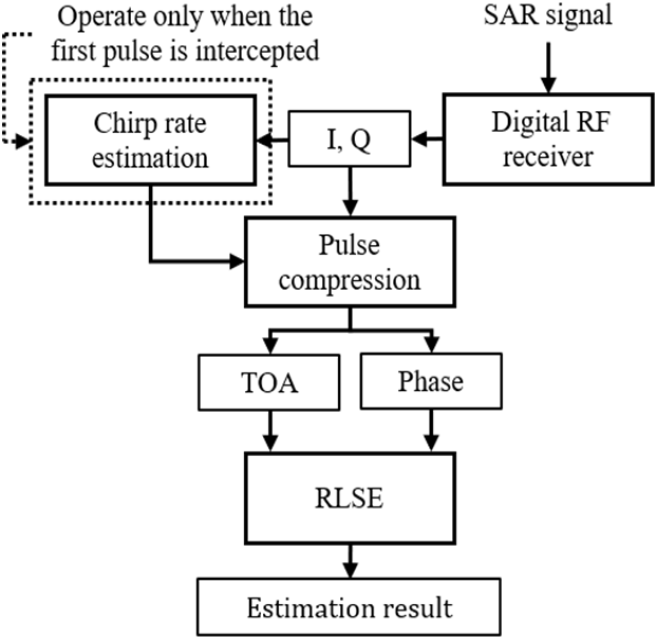
Ⅱ장에서 서술한 한계점을 극복하기 위해, 본 장에서는 현재 수신된 SAR 신호로부터 펄스 압축 및 RLSE를 통해 다음번 SAR 신호의 송신 시점 및 중심 주파수를 추정하는 기법을 제안한다. 제안하는 추정 기법은 그림 2와 같이 디지털 RF 수신기를 통해 수신된 I(in-phase)와 Q (quadrature-phase)를 실시간으로 압축하고, 압축된 신호의 피크 지점에서 도착 시간과 위상을 측정한다. 측정된 도착 시간과 위상은 RLSE의 입력으로 들어가며, 출력으로 신호의 중심 주파수와 다음 송신 시점의 추정 결과를 획득한다.

그림 2. | Fig. 2. 제안하는 SAR 파라미터 추정 기법 블록도 | Block diagram of the proposed estimation method for SAR parameters.

Download Original Figure

제안하는 기법을 설명하기에 앞서, RLSE에 대해 먼저 간략히 소개한다. 그 후 기존 기법들의 한계점을 극복할 수 있는 새로운 기만 재밍 기법에 대하여 설명하고, 본 장의 Ⅲ절에서 제안하는 추정 기법을 구체적으로 서술한다. 또한 제안하는 기법을 서술함에 있어 현재 수신된 신호는 n번째 신호를, 그 다음번에 수신된 신호는 n+1번째 신호를 의미함을 알린다.

3-2 제안하는 기만 재밍 기법

기존 기만 재밍 기법의 핵심은 허위 표적 위치 좌표에서 반사된 SAR 신호가 SAR에 수신되는 시점에 맞춰 기만 신호를 방사하는 것이다. 반면 제안하는 기만 재밍 기법은 이 핵심을 그대로 유지하되, 이전에 수신된 SAR 신호로부터 파라미터를 추정하고, 이를 활용해 현재 SAR 신호가 재머에 수신되기 전에 기만 신호를 방사하는 것이다. 그림 3(a) 및 그림 3(b)는 각각 기존의 기만 재밍 기법과 제안하는 기만 재밍 기법에 대한 특정 방위 시각의 SAR와 재머의 송, 수신 흐름도를 나타낸다. 여기서 t_{jmr, Tx}, t_{jmr, Rx}, t_{sar, Tx}, t_{sar, Rx}는 각각 재머의 기만 신호 방사 시점, 재머의 SAR 신호 수신 시점, SAR 신호 송신 시점, SAR 신호 수신 시점을 의미하며, 일직선상에 시간의 흐름을 표현하기 위해 편의상 SAR의 송, 수신을 따로 구분하였다. 또한 R_J/c와 R_F/c는 각각 SAR와 재머 간의 거리와 SAR와 허위 표적 간의 거리에 따른 단방향 시간 지연을 나타낸다.

그림 3. | Fig. 3. SAR와 재머의 송/수신 흐름도 | Flow chart of transmission/reception in SAR and jammer.

Download Original Figure

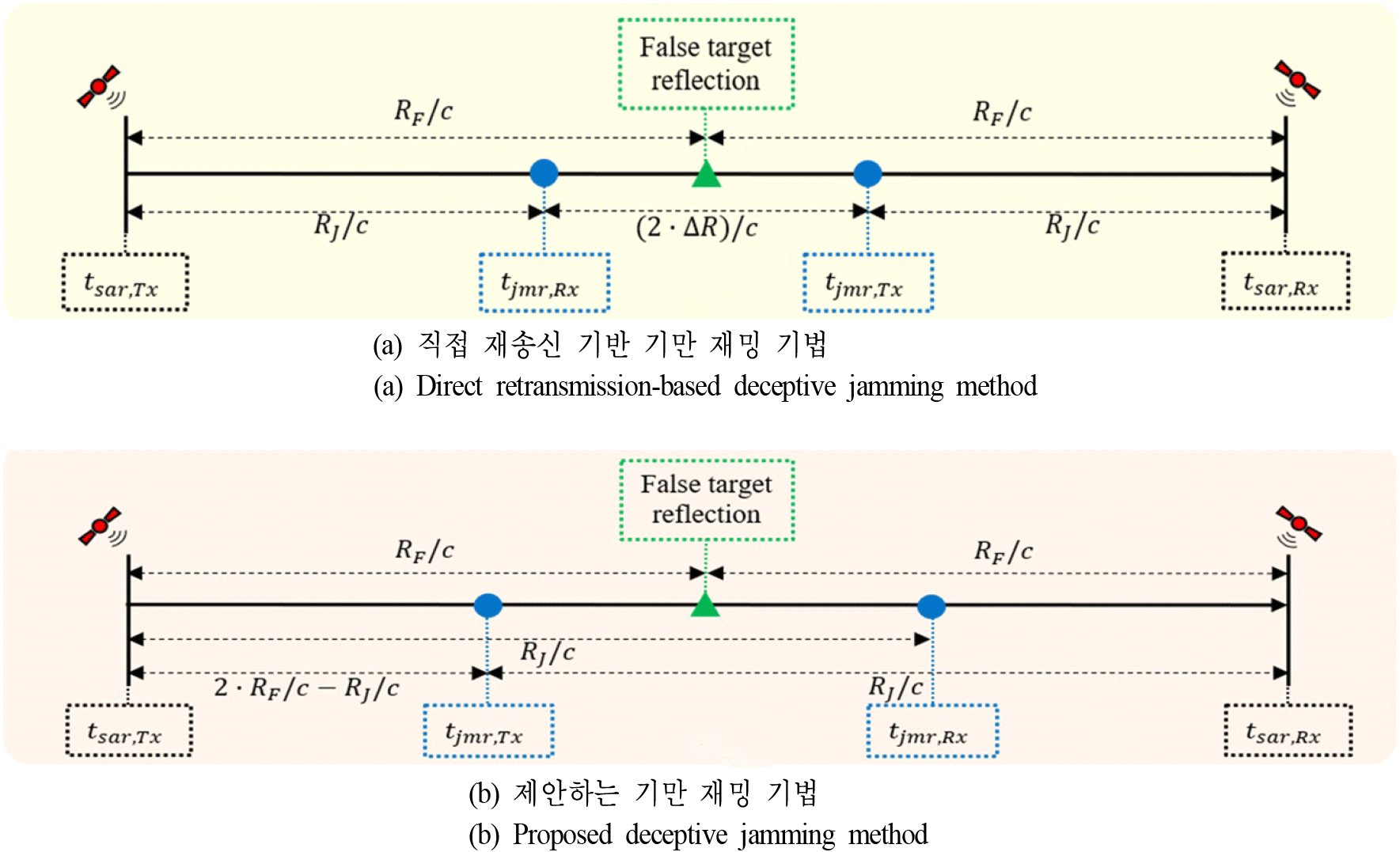
그림 3(a)를 보면 기존의 기만 재밍 기법은 재머에서 SAR 신호를 수신하고, 수신된 신호에 특정 시간 지연을 적용한 후 SAR를 향해 방사하는 것을 볼 수 있다. 반면 그림 3(b)를 보면 이전 신호로부터 추정된 현재 SAR 신호의 송신 시점을 알기 때문에, 재머의 기만 신호 방사 시점을 식 (5)와 같이 설정할 수 있다.

$$t_{jmr,Tx}=t_{sar,Tx}+\left(\frac{2R_F\left(t_{sar,Tx}\right)}{c}-\frac{R_J\left(t_{sar,Tx}\right)}{c}\right).$$

(5)

여기서 R_J와 R_F는 사전에 수집한 위성의 궤도 정보를 통해 계산한다고 가정한다. 상기 수식과 같이 기만 신호 방사 시점을 설정함으로써 허위 표적의 위치를 재머의 위치와 상관없이 SAR의 관심 영역 내에서 자유롭게 설정할 수 있다.

제안하는 기만 재밍 기법은 사전에 생성된 기만 신호를 설정된 기만 신호 방사 시점에 SAR를 향해 방사한다. 방사 시 기존의 기법처럼 수신된 신호를 활용하는 것이 아니기 때문에, 기저대역에서 RF 대역으로의 주파수 상향 변환이 요구된다. 이를 위해 수신기를 통해 탐지된 SAR 신호의 중심 주파수를 간단하게 측정하여 사용할 수 있지만, 주파수 측정 해상도에 의해 수 kHz에서 수십 kHz의 오차를 포함한다. 이 같은 오차로 인한 SAR와 재머의 중심 주파수 차이는 SAR 신호처리 시 위상 천이를 초래하고, 이는 방위축에서의 허위 표적 위치 오차를 발생시킨다. 따라서 이를 방지하기 위해, 본 논문에서는 수신된 SAR 신호로부터 중심 주파수를 정확하게 추정하고, 이를 재머의 중심 주파수로 사용한다.

3-3 제안하는 다음번 SAR 신호 송신 시점 및 중심 주파수 추정 기법

디지털 RF 수신기는 원하는 주파수 대역 사이의 주파수 신호를 RF 밴드 패스 필터와 아날로그 디지털 변환기 등을 거쳐 I, Q로 변환한다. 본 논문에서는 관심 주파수 대역을 X 대역으로 설정하고, 균일한 대역폭을 가지는 RF 밴드 패스 필터 i개를 사용하여 X 대역의 SAR 신호가 탐지되었다고 가정하였다. 탐지되어 기저대역으로 변환된 SAR 신호 r(t)는 식 (6)과 같이 나타낼 수 있다^[1].

$$\begin{array}{c}r(t)=s(t-\tau )\exp \left\{-j2\pi f_{\text{sarr }}\tau \right\}\\ \times \exp \left\{j2\pi \left(f_{\text{sarr }}-f_{\text{jmr }}\right)t\right\}\\ \times \exp \left\{j\left({\psi }_{\text{sar }}-{\psi }_{\text{jmr }}\right)\right\}.\end{array}$$

(6)

여기서 s(t)는 위성 SAR에서 일반적으로 사용되는 처프(chirp) 펄스 신호를 의미하며, τ는 SAR와 재머 간의 거리에 따른 단방향 시간 지연, f_sar, f_jmr는 SAR와 재머의 중심 주파수, ψ_sar, ψ_jmr는 초기 SAR와 재머의 국부 발진기 위상을 나타낸다.

기저대역의 SAR 신호는 디지털 신호로 변환되어 복소수 샘플로 표현되며, 변환된 신호와 정합 필터 간의 콘볼루션을 통해 펄스 압축을 수행한다^[1]. 여기서 정합 필터는 재머의 동작 이후 가장 먼저 수집된 SAR 신호 샘플로부터 처프 비율(chirp rate)을 추정하고, 추정된 처프 비율로부터 정합 필터를 생성하여 사용한다. 처프 비율의 추정은 신호 샘플들의 위상값으로부터 순시 주파수를 구하고, 순시 주파수에 대한 선형 회귀를 통하여 추정할 수 있다. 거리 포락선이 구형 함수인 펄스는 압축되면서 싱크 함수 형태로 변환되고, 그와 동시에 신호 대 잡음비(SNR, signal-to-noise ratio)가 크게 증가한다. 따라서 압축된 펄스를 제외한 성분들의 크기는 압축된 펄스의 크기에 비해 작기 때문에, 피크 지점을 찾음으로써 신호의 도착 시간과 위상을 매우 높은 정확도로 측정할 수 있다.

3-3-1 SAR 신호 송신 시점 추정 기법

측정된 도착 시간으로부터 RLSE를 통해 다음 신호의 송신 시점을 추정하기 위해, 본 논문에서는 정합 필터가 생성된 이후 재머에 수신된 첫 번째 신호의 송신 시점 Tx₁과 펄스 반복 주기(PRI, pulse repetition interval)를 추정하고자 하는 변수로 설정하고, 추정된 두 변수를 통해 식 (7)과 같이 다음 신호의 송신 시점을 추정하였다.

$${\widehat{t}}_{n+1,Tx}=T{x}_1+n\times PRI.$$

(7)

여기서 ${\widehat{t}}_{n+1,Tx}$는 현재 신호가 수신되었을 때 추정된 다음 신호의 송신 시점이며, 펄스 반복 주기는 일정하다고 가정하였다. 상태 벡터 x는 추정하려는 변수 Tx₁과 PRI로 구성되며, 이때 측정값 z_n은 현재 수신된 신호의 송신 시점으로 설정함으로써 RLSE의 측정값에 대한 가정을 식 (8)과 같이 만족할 수 있다.

$$z_n=H_{n}x+v_n=\left[\begin{array}{c}1n-1\end{array}\right]\left[\begin{array}{l}T{x}_1\hfill \\ PRI\hfill \end{array}\right]+v_n.$$

(8)

측정값을 현재 수신된 신호의 송신 시점으로 설정함에 따라, 본 논문에서는 측정된 도착 시간과 SAR, 재머 간의 거리에 따른 시간 지연을 통해 현재 수신된 신호의 송신 시점을 획득하였다. 그림 4와 같이 SAR 신호가 고정 PRI로 송신되고, 현재 송신 신호가 재머에 수신될 때의 도착 시간을 t_n,TOA라고 할 때, 이 신호의 송신 시점 t_n,Tx는 식 (9)와 같이 나타낼 수 있다.

$$t_{n.Tx}=t_{n.TOA}-\tau \left(t_{n,Tx}\right).$$

(9)

그림 4. | Fig. 4. SAR의 송신(위쪽)과 재머의 수신(아래쪽) 시점 | Timing of SAR transmission (upper) and jammer reception (lower).

Download Original Figure

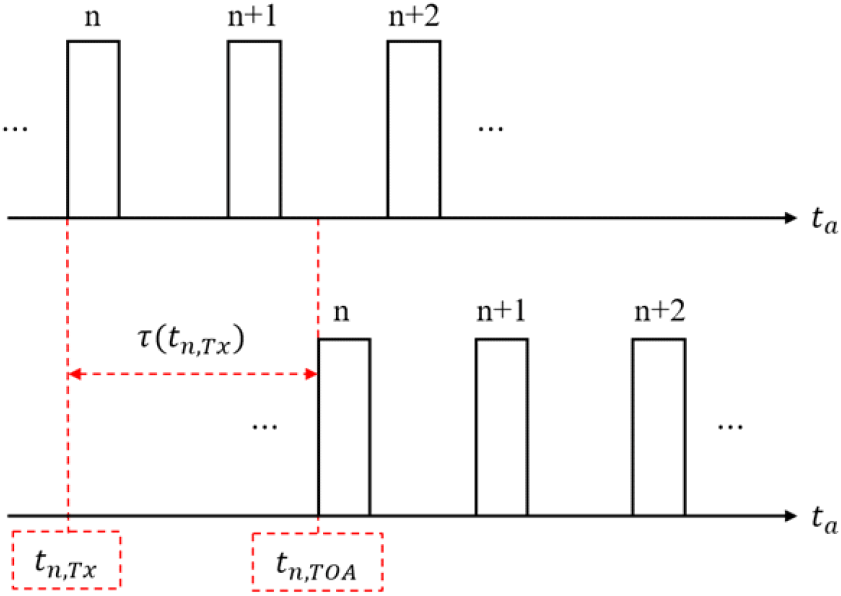
여기서 τ(t_n,Tx)는 송신 시점이 t_n,Tx일 때, SAR와 재머의 단방향 시간 지연을 의미하며, 식 (10)과 같이 표현된다.

$$\tau \left(t_a\right)=\frac{\left|\text{SJ}\right|}{c}=\frac{R_J\left(t_a\right)}{c}.$$

(10)

하지만 식 (9)는 t_n,Tx를 계산하는데 t_n,Tx가 필요하게 된다. 이와 같은 문제를 해결하기 위해, 본 논문에서는 도착 시간을 통해 단방향 시간 지연을 계산할 수 있는 함수를 다항식 곡선 피팅을 통해 생성한다^[23]. 피팅된 단방향 시간 지연 함수 $\tilde{\tau }\left(t_a^{\prime }\right)$는 피팅 전 단방향 시간 지연 함수 τ(t_a)와 식 (11)과 같은 관계를 가진다.

$$\tau \left(t_a\right)=\tilde{\tau }\left(t_a^{\prime }\right)=\tilde{\tau }\left(t_a+\tau \left(t_a\right)\right),t_a^{\prime }=t_a+\tau \left(t_a\right).$$

(11)

따라서 측정된 도착 시간과 피팅된 단방향 시간 지연 함수를 통해, 현재 신호의 송신 시점을 식 (12)와 같이 계산할 수 있다.

$$t_{n,Tx}=z_n=t_{n,TOA}-\tilde{\tau }\left(t_{n,TOA}\right).$$

(12)

최종적으로 제안하는 SAR 신호 송신 시점 추정 기법은 도착 시간으로부터 측정값을 획득하고, 초기화된 상태 벡터와 오차 공분산의 업데이트를 알고리듬 1과 같이 수행함으로써 다음 신호의 송신 시점을 추정할 수 있다. 여기서 상태 벡터의 초기화는 n = 1일 때 Tx₁을 첫 번째 측정값으로 초기화하고, n = 2일 때 PRI를 두 번째 측정값과 첫 번째 측정값의 차로 초기화한다. 또한 측정 잡음 공분산과 추정 오차 공분산 행렬의 초기화는 샘플 간격에 기인한 측정 오차에 기반하여 초기화한다.

3-3-2 SAR 신호 중심 주파수 추정 기법

측정된 위상으로부터 RLSE를 통해 신호의 중심 주파수를 추정하기 위해, 본 논문에서는 SAR와 재머의 중심 주파수 차 Δf(= f_sar − f_jmr)와 SAR와 재머의 초기 국부 발진기 위상의 차 Δψ(=ψ_sar − ψ_jmr)을 추정하고자 하는 변수로 설정하였다. 이때 Δψ는 Δf를 추정하는데 사용되는 변수이며, 신호의 중심 주파수를 추정하는 직접적으로 관여하지 않는다. 신호의 중심 주파수는 재머의 중심 주파수를 이미 알고 있으므로 Δf를 추정함으로써 쉽게 추정할 수 있다. 상태 벡터 x는 추정하려는 변수 Δf와 Δψ로 구성되며, 측정값 z_n은 식 (13)과 같이 설정한다.

$$z_n=\exp \left\{j{\varphi }_n\right\}+2\pi f_{jmr}\tilde{\tau }\left(t_{n,TOA}\right).$$

(13)

알고리듬 1. | Algorithm 1. SAR 신호 송신 시점 추정 기법 | Estimation method for the transmission time of SAR signals.

Download Original Figure

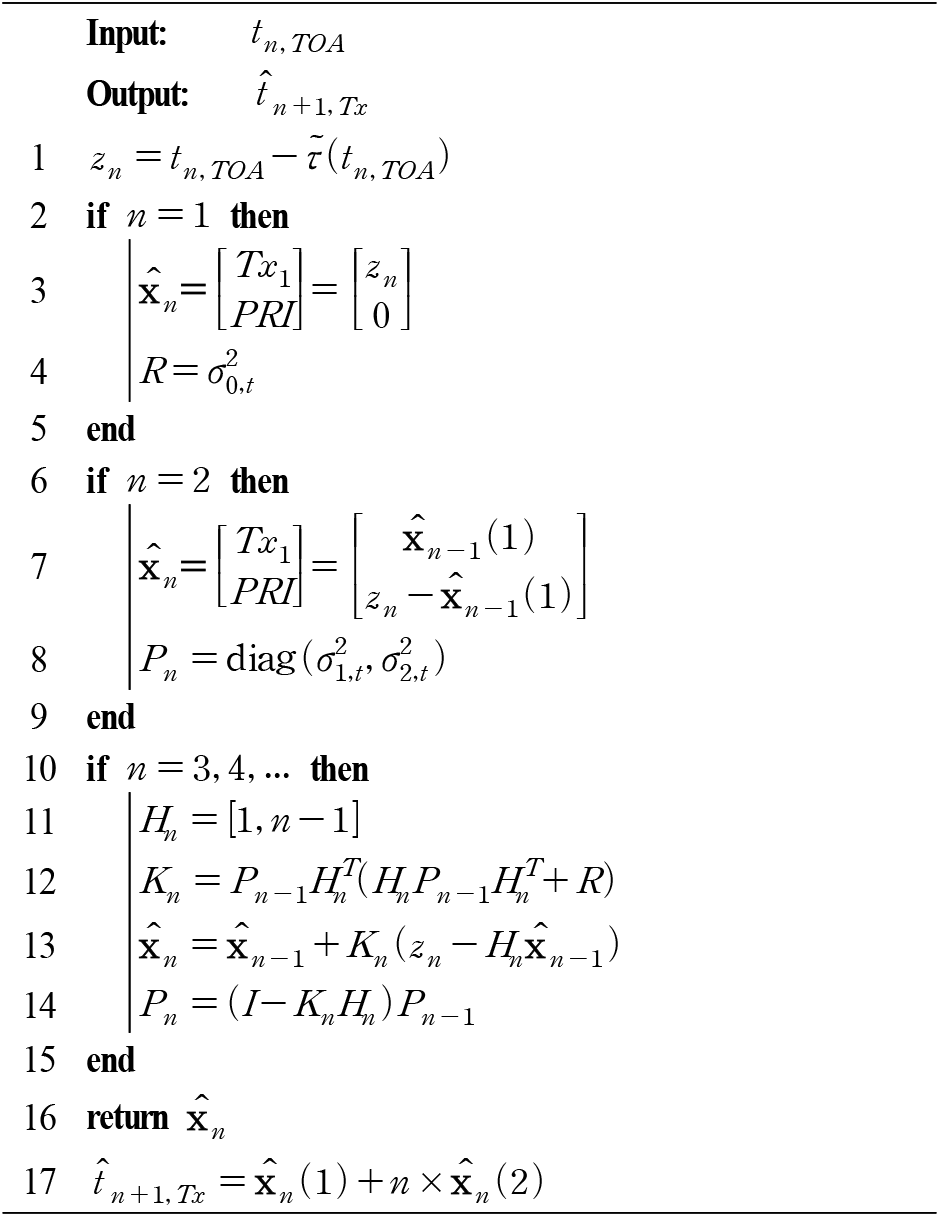
여기서 exp{jϕ_n}는 피크 지점에서 측정된 현재 수신된 신호의 접힌(wrapped) 위상, ϕ_n은 펼친(unwrapped) 위상이며, 식 (6)의 SAR 신호 모델로부터 식 (14)와 같이 정리할 수 있다.

$$\begin{array}{c}{\varphi }_n=-2\pi \left(\text{Δ}f+f_{jmr}\right)\tilde{\tau }\left(t_{n,TOA}\right)\\ +2\pi \text{Δ}f{t}_{n,TOA}+\text{Δ}\psi \\ =-2\pi f_{jmr}\tilde{\tau }\left(t_{n,TOA}\right)+2\pi \text{Δ}f{t}_{n,Tx}+\text{Δ}\psi .\end{array}$$

(14)

이때 측정값에 대한 가정이 선형 방정식이므로, 접힌 위상에 의한 모호성 문제를 방지하기 위해 측정값을 펼친 위상으로 변환하여 사용한다. 이에 따라 수신된 신호의 펼친 위상을 측정값에 대하여 정리한다면 RLSE의 측정값에 대한 가정을 식 (15)와 같이 만족할 수 있다.

$$\begin{array}{c}{Z}_n=H_{n}x+v_n=\left[2\pi t_{n,Tx}1\right]\left[\begin{array}{c}\text{Δ}f\\ \text{Δ}\psi \end{array}\right]+v_n,\\ Z_n=unwrap\left[z_n\right].\end{array}$$

(15)

여기서 unwrap[·]은 접힌 위상을 펼친 위상으로 변환해주는 함수를 의미한다.

최종적으로 제안하는 SAR 신호 중심 주파수 추정 기법은 도착 시간과 위상으로부터 측정값을 획득하고, 초기화된 상태 벡터와 오차 공분산의 업데이트를 알고리듬 2와 같이 수행함으로써 신호의 중심 주파수를 추정할 수 있다. 상태 벡터의 초기화는 n = 1일 때 Δf와 Δψ를 모두 0으로 초기화하며, 이는 Δf를 초기화하는데 현재 측정값과 이전 측정값의 차가 사용되고, Δψ를 초기화하는데 Δf가 사용되기 때문이다. n = 2일 때 Δf는 식 (16)과 같이 초기화한다.

$$\text{Δ}f=\frac{Z_n-Z_{n-1}}{2\pi \left(t_{n,Tx}-t_{n-1,Tx}\right)}.$$

(16)

알고리듬 2. | Algorithm 2. SAR 신호 중심 주파수 추정 기법 | Estimation method for the center frequency of SAR signals.

Download Original Figure

상기 수식은 현재 신호와 이전 신호 간의 펼친 위상차를 Δf에 대하여 정리함으로써 유도할 수 있다. 초기화된 Δf를 통해 n = 2일 때 Δψ는 식 (17)과 같이 초기화한다.

$$\text{Δ}\psi =Z_n-2\pi t_{n,Tx}\text{Δ}f.$$

(17)

상기 수식은 펼친 위상으로부터 Δψ에 대하여 나타냄으로써 유도할 수 있으며, 측정 잡음 공분산과 추정 오차 공분산 행렬의 초기화는 열잡음에 기반하여 초기화한다.

Ⅳ. 모의실험

제안하는 기법의 파라미터 추정 성능을 확인하기 위해 표 1에 나타낸 환경을 기반으로 모의실험을 진행하였다. 여기서 표 1의 B, PRF, PW, f_s는 각각 SAR의 신호 대역폭, 펄스 반복 주파수, 펄스 폭, 재머의 샘플링 주파수를 의미하며, ${\sigma }_{0,t}^2,{\sigma }_{1,t}^2,{\sigma }_{2,t}^2$는 각각 알고리듬 1의 측정 잡음 공분산, 추정 오차 공분산 행렬의 대각 성분, ${\sigma }_{0,t}^2,{\sigma }_{1,t}^2$,${\sigma }_{2,t}^2$는 각각 알고리듬 2의 측정 잡음 공분산, 추정 오차 공분산 행렬의 대각 성분을 나타낸다. 재머의 위치 좌표는 LLA(latitude-longitude-altitude) 좌표로 [36, 128, 0]으로 설정한 후, ECEF(earth-centered earth-fixed) 좌표로 변환하여 사용하였으며, SAR의 궤도 정보는 ICEYE-X20에 대한 TLE(two-line element)로부터 획득하여 사용하였다^[24]. 시뮬레이션 시간은 23년 7월 12일 05시 25분 14.5초부터 15.5초까지 1초로 설정하였으며, 14.5초에 첫 번째 SAR 신호가 송신된 것으로 시나리오를 설정하였다. SAR에서 송신된 신호는 자유 공간 경로 손실을 겪는다고 가정하였으며, 재머에 수신되는 신호의 SNR은 자유 공간 경로 손실과 송, 수신 안테나 이득, 잡음지수 등을 현실적으로 고려하여 15 dB로 설정하였다. 분석의 편의를 위해 초기화 단계(n = 1, 2)에서의 추정값은 제외하고 파라미터 추정 결과를 도시하였다.

그림 5는 제안하는 SAR 신호 송신 시점 추정 기법을 통해 추정된 다음 신호의 송신 시점에 대한 오차를 나타낸다. 여기서 오차는 추정된 결괏값에서 참값을 뺀 값을 의미한다. 그림 5를 보면 추정된 송신 시점의 오차가 대략 0.01 ns 이하로, 샘플링 간격보다 작은 값으로 수렴하며 매우 정밀하게 추정되는 것을 볼 수 있다. 또한 대략 100번째 펄스부터 추정 결과가 수렴하기 때문에, SAR 신호가 재머에 수신된 이후 100번째 펄스부터 추정된 결과를 활용하여 허위 표적의 위치를 자유롭게 설정할 수 있다.

그림 5. | Fig. 5. SAR 신호 송신 시점 추정 오차 | Estimation error for the transmission time of SAR signals.

Download Original Figure

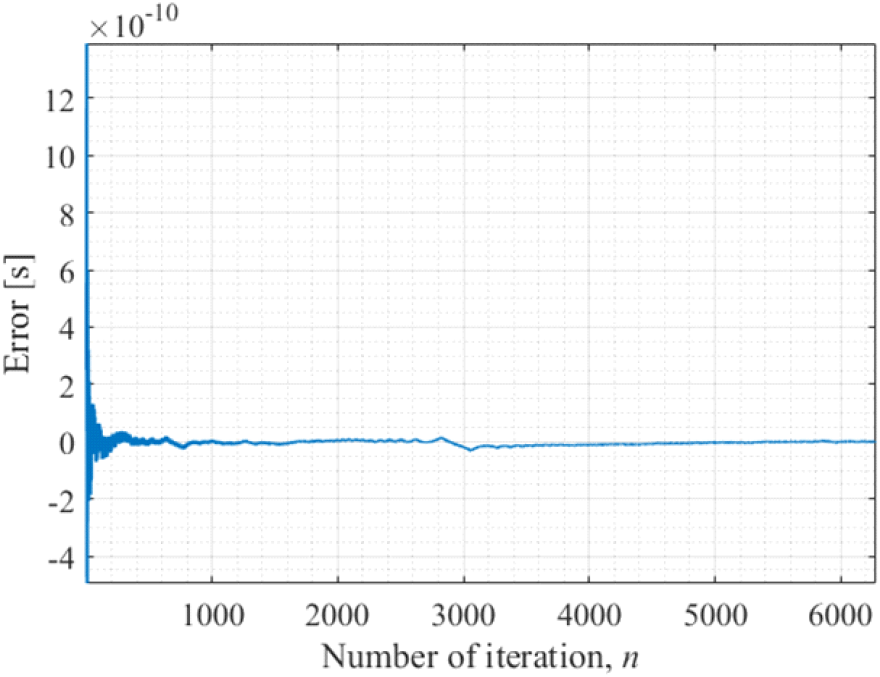
그림 6은 재머의 중심 주파수가 SAR의 중심 주파수보다 3 kHz 클 때, 제안하는 SAR 신호 중심 주파수 추정 기법을 통해 추정된 Δf를 나타낸다. 그림 6을 보면 수신되는 펄스 개수가 증가함에 따라 주파수 차이가 0.1 Hz 미만의 오차를 가지고 −3 kHz로 수렴하며 매우 정확하게 추정되는 것을 볼 수 있다. 또한 대략 50번째 펄스부터 0.1 Hz 미만의 오차를 가지고 추정 결과가 수렴하기 시작하며, 수렴된 추정 결과를 바탕으로 재머의 중심 주파수를 설정하여 주파수 상, 하향 변환을 정확하게 수행할 수 있다.

그림 6. | Fig. 6. 모호성이 없는 SAR와 재머의 중심 주파수 차이 추정 오차 | Estimation error for the center frequency difference between SAR and jammer without ambiguity.

Download Original Figure

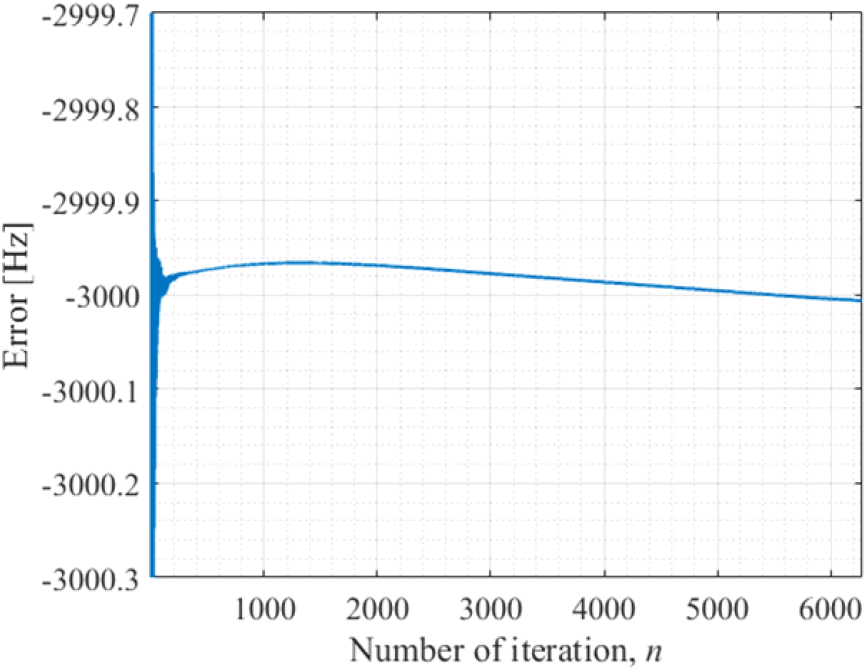
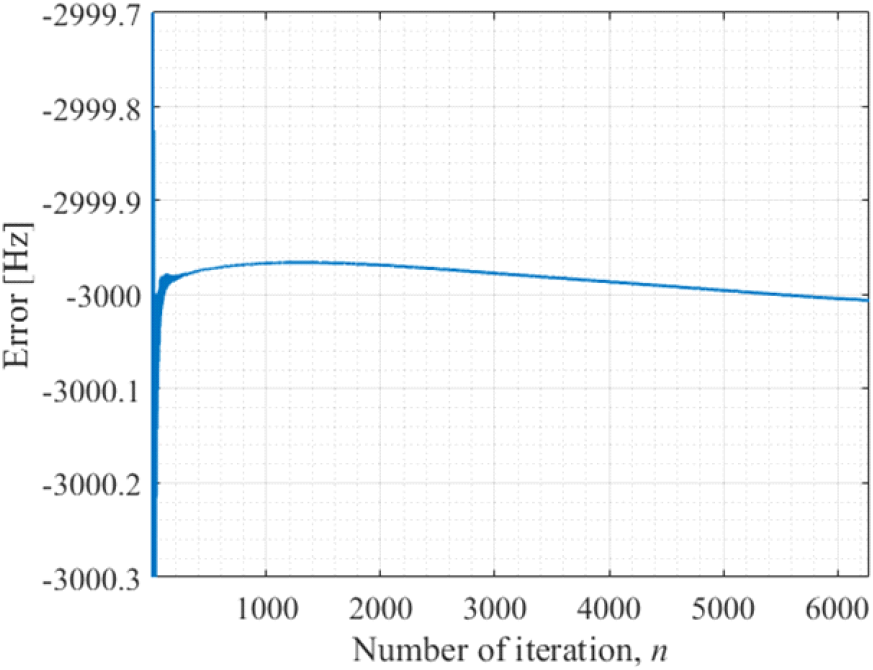
그림 7은 재머의 중심 주파수가 SAR의 중심 주파수보다 65.8309 kHz 클 때, 제안하는 SAR 신호 중심 주파수 추정 기법을 통해 추정된 Δf를 나타낸다. 추정된 결과를 보면 그림 6의 결과와 동일하게 Δf가 −3 kHz로 수렴하는 것을 볼 수 있다. 이러한 결과는 재머와 SAR의 중심 주파수 차가 PRF의 절반보다 커서 모호성이 발생했기 때문이다. 모호성이 발생했을 때의 추정된 결과를 기반으로 재머의 중심 주파수를 설정한다면, SAR의 중심 주파수보다 PRF의 배수 배만큼 크거나 작게 설정될 것이고, 해당 중심 주파수를 가지는 반송파에 기만 신호가 실려 SAR을 향해 방사될 것이다. 하지만 SAR 또한 신호처리 과정에서 방위축으로 PRF에 의한 모호성이 존재한다. 따라서 SAR와 재머의 중심 주파수가 PRF의 배수 배만큼 차이가 나더라도, 방위축에서 허위 표적의 위치 오차가 발생하지 않는다. 결과적으로 제안하는 SAR 신호 중심 주파수 추정 기법을 통해 SAR의 중심 주파수가 정확하게 추정되거나, SAR의 중심 주파수보다 PRF의 배수 배만큼 크거나 작은 값으로 추정이 되지만, 이를 통해 주파수 상향 변환을 하더라도 방위축 상에서 허위 표적을 의도한 위치에 형성할 수 있다.

그림 7. | Fig. 7. 모호성이 있는 SAR와 재머의 중심 주파수 차이 추정 오차 | Estimation error for the center frequency difference between SAR and jammer with ambiguity.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 기존의 기만 재밍 기법에서 존재하는 한계점을 해결하기 위한 새로운 기만 재밍 기법 연구의 일환으로서, 현재 수신된 SAR 신호로부터 펄스 압축 및 RLSE를 통해 신호의 다음 송신 시점 및 중심 주파수를 추정하는 기법을 제안하였다. 제안하는 추정 기법은 수신된 신호로부터 실시간으로 다음 신호의 송신 시점을 샘플링 간격 이내로, 신호의 중심 주파수를 0.1 Hz 미만의 오차로 정확하게 추정할 수 있으며, 모의실험을 통해 이를 확인하였다. 추정된 파라미터는 기만 신호 방사 시점을 결정하고, 사전에 기저대역에서 생성된 기만 신호를 RF 대역으로 변환하는 데 사용되며, 이를 통해 허위 표적 위치 설정에 대한 한계점을 극복할 수 있다.

다만 제안하는 기만 재밍 기법은 수신된 SAR 신호를 활용하지 않고 SAR의 특성을 반영한 기만 신호를 직접 생성해야 한다. 또한 TLE로부터 획득한 위성의 궤도 정보에 오차가 포함될 수 있고, 추정된 파라미터 또한 이에 의한 오차가 포함될 수 있다. 따라서 향후에는 이러한 점들을 고려하여 제안하는 기만 재밍 기법에 관한 구체적인 연구를 수행하고, 위성 궤도 오차가 허위 표적 형성에 미치는 영향을 분석할 예정이다.