비스듬히 입사하는 평면파에 대한 평판형 손실 소재의 차폐 특성

Ⅰ. 서 론

평판형 소재의 원역장 전자파 차폐효과(SE)는 일반적으로 수직 입사 조건에서 많이 해석되고 측정도 이루어진다^[1]-[3]. 2차원 평면상에 두 매질의 경계면이 형성되어 있는 경우, 그 경계면에 비스듬히 입사하는 평면파에 의한 반사와 투과 현상은 전기장이 평면(구조 단면)에 직각을 이루는 직각(perpendicular) 편파와 전기장이 평면상에 놓여 있는 평행(parallel) 편파로 나누어 해석한다^[4]. 서로 다른 두 매질의 경계면에서 일어나는 반사 특성이 입사 편파에 따라 다르기 때문이다. 한편, 매질의 손실을 고려할 경우에는 매질 내로 입사된 전자파의 굴절각이 복소수가 되며, 이는 매질 내 전자파의 흡수 특성과 연관된다. 비스듬히 입사하는 평면파에 대해 소재의 차폐 특성을 해석할 때 3차원 수치해석 툴을 사용하는 경우, 유한한 해석 공간에서 소재에 의한 반사와 투과를 정확하게 해석하려면 경계면에 흡수경계조건을 적용해야 하지만, 소재가 해석 경계면과 만나게 되면 이를 사용하는데 어려움이 발생하고, 이로 인해 정확한 결과를 얻기 힘들다^[5]. 결론적으로 지금까지 비스듬히 입사하는 평면파에 대해 무한한 크기의 유한한 두께를 가지는 평판형 손실 소재의 차폐 특성을 분석한 사례는 많지 않았다^[6].

본 논문에서는 직각 및 평행 편파를 갖는 비스듬히 입사하는 평편파에 대해 두께를 가지는 평판형 소재의 SE 이론식을 유도하고, 유전 및 자성 흡수 소재의 차폐 특성을 분석하였다. 입사 각도와 소재의 두께에 따른 각 소재의 차폐 특성을 Schelkunoff가 정의한 반사, 흡수, 그리고 다중반사손실의 영향으로 나누어 분석하였다.

Ⅱ. 비스듬히 입사하는 평면파에 대한 평판형 소재의 차폐효과 계산

수직으로 입사하는 평면파에 의한 소재의 투과율(T)은 소재의 경계면에서 경계조건을 이용하여 다음과 같이 얻을 수 있다^[3].

여기서 ρ = (η − η₀)/(η + η₀)는 반사계수, ${\eta }_0=\sqrt{{\mu }_0/{ϵ}_0}$, $\eta =\sqrt{j\omega \mu /\left(\sigma +j\omega \in \right)}$, ${\beta }_0=\omega \sqrt{{\mu }_0{\in }_0}$, $\gamma =\sqrt{j\omega \mu /\left(\sigma +j\omega \in \right)}\text{이며}$, ω=2πf로 입사 평면파의 각주파수이다.

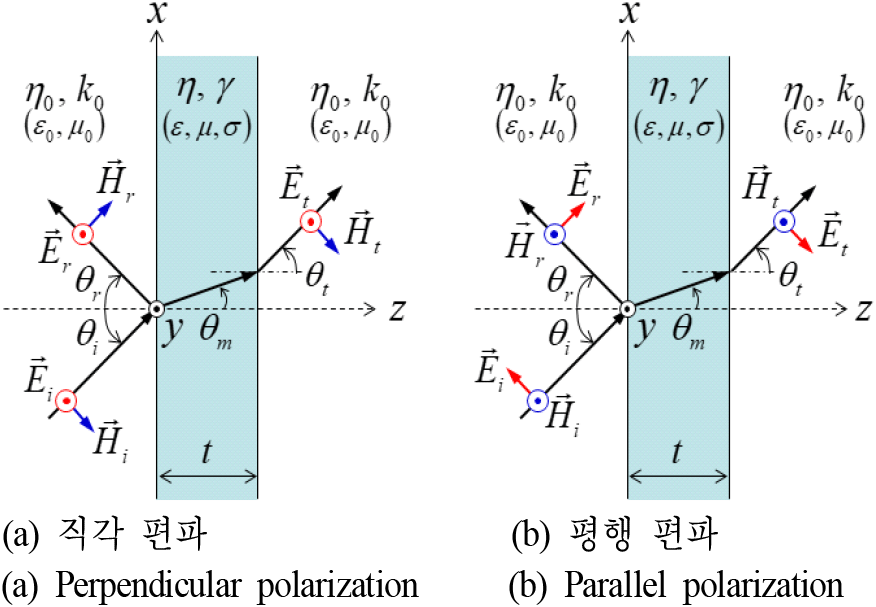
비스듬히 입사하는 평면파에 대한 소재의 투과율은 그림 1에서 보듯이 직각 및 평행 편파로 나누어 해석한다. 수직 입사의 경우와 동일한 방법으로 경계조건을 적용하면 다음과 같은 투과율을 얻을 수 있다.

그림 1. | Fig. 1. 평판형 소재에 비스듬히 입사하는 평면파의 반사와 투과 | Reflection and transmission of plane waves obliquely incident on a planar material.

Download Original Figure

여기서 ρ_o는 소재 입사면에서 비스듬히 입사하는 평편파의 반사계수로 표 1과 같이 직각 및 평행 편파에 대해 입사각(θ_i)과 소재 내에서의 굴절각(θ_m)의 함수로 나타난다.

결과적으로 비스듬히 입사하는 평면파에 대한 소재의 SE는 다음과 같이 정의된다.

여기서 $S{E}_R=-20{\log }_{10}\left|1-{\rho }_0^2\right|$, $S{E}_A=20{\log }_{10}\left|e^{\gamma t\cos {\theta }_m}\right|$, $S{E}_M=20{\log }_{10}\left|1-{\rho }^2{e}^{-2\gamma t\cos {\theta }_m}\right|\text{이며}$, 이는 Schelkunoff가 정의한 반사손실(SE_R), 흡수손실(SE_A), 그리고 다중반사손실(SE_M)에 해당된다^[7].

Ⅲ. 분석 결과 및 검증

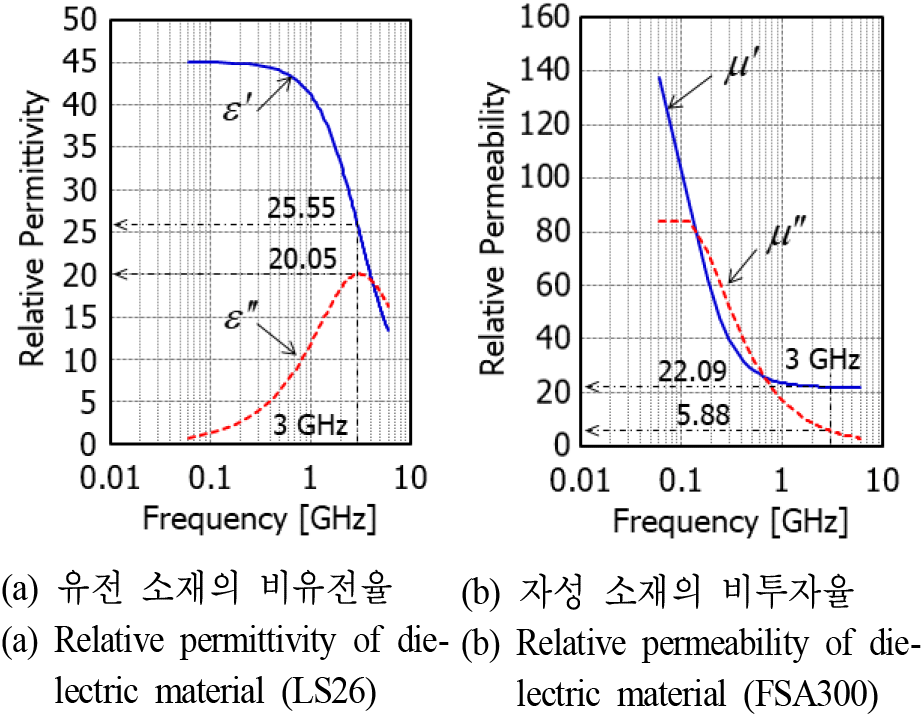
본 절에서 식 (2) 및 식 (3)을 이용하여 유전 및 자성 흡수 소재에 대한 SE를 분석하였다. 유전 소재는 Laird사의 Eccosorb LS26 모델을 사용하였고^[8], CST MWS (Microwave Studio)^[6]에서 주파수에 따른 복소 유전율을 제공한다. 자성 소재는 GSS사의 FSA300 모델을 사용하였고^[9], 측정을 통해 복소 투자율을 추출하였다. 그림 2에서는 분석에 사용된 두 흡수 소재의 비유전율과 비투자율을 도시하였다.

그림 2. | Fig. 2. 유전 및 자성 손실 소재의 물성 | Material properties of dielectric and magnetic lossy materials.

Download Original Figure

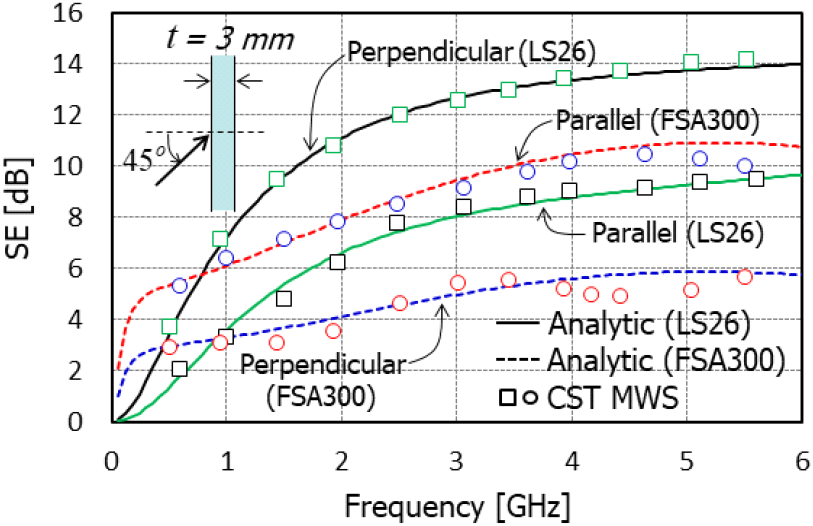
그림 3에서는 45°C로 입사하는 평면파에 의한 3 mm 두께의 유전 및 자성 흡수 소재들의 SE를 6 GHz까지 비교하였다. 유전 흡수 소재의 경우, 직각 편파가 평행 편파에 비해 최대 4 dB 정도 높은 SE를 보인다. 반면, 자성 흡수 소재는 평행 편파가 직각 편파에 비해 더 높은 SE를 보인다. 유전 흡수 소재가 자성 흡수 소재에 비해 SE가 높으나, 1 GHz 이하의 낮은 주파수 대역에서는 자성 흡수 소재의 SE가 더 높게 나타난다. 이는 그림 2에서도 보듯이 저주파수 대역에서 자성 소재의 투자율이 유전 소재의 유전율보다 높기 때문이다. 한편, 해석적인 해의 정확도를 검증하기 위해서 CST MWS를 이용하여 유전 및 자성 소재의 SE를 계산하여 비교하였고, 직각 편파와 평행 편파에서 모두 잘 일치함을 알 수 있다.

그림 3. | Fig. 3. 45°C로 입사하는 평면파에 의한 유전 및 자성 흡수 소재들의 차폐효과 비교 | Comparison of SEs of dielectric and magnetic absorbing materials by plane wave incident at 45°C.

Download Original Figure

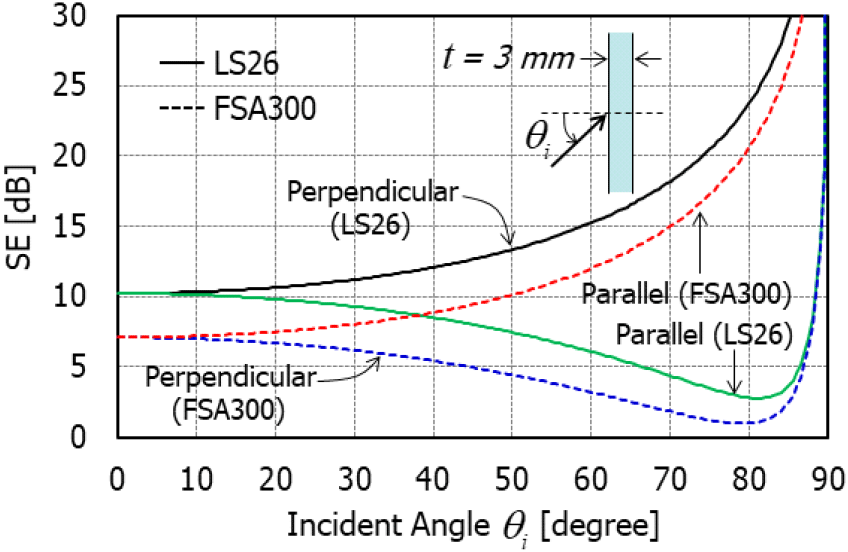
그림 4에서는 입사 각도에 따른 3 mm 두께의 유전 및 자성 흡수 소재들의 SE를 3 GHz에서 비교하였다. 이는 그림 2에서 3 GHz에서의 비유전율과 비투자율 값을 이용하여 계산한 것이다. 유전 흡수 소재의 경우에 입사 각도가 증가함(더 비스듬히 입사함)에 따라 직각 편파의 SE는 증가하고, 평행 편파의 SE는 감소하다가 80°C 이상의 입사 각도에서 급격히 증가한다. 반면, 자성 흡수 소재의 경우에 입사 각도가 증가(더 비스듬히 입사)함에 따라 평행 편파의 SE는 증가하고, 직각 편파의 SE는 감소한다. 이는 두 소재의 반사계수가 편파에 따라 서로 상반된 값을 가지기 때문인데, 편파와 입사각에 따라 크게 변하는 공기의 임피던스와 그렇지 않은 소재의 임피던스 차이 때문이다.

그림 4. | Fig. 4. 유전 및 자성 흡수 소재들의 입사 편파에 따른 3 GHz에서의 차폐효과 비교 | Comparison of SEs at 3 GHz of dielectric and magnetic absorbing materials by incident polarization.

Download Original Figure

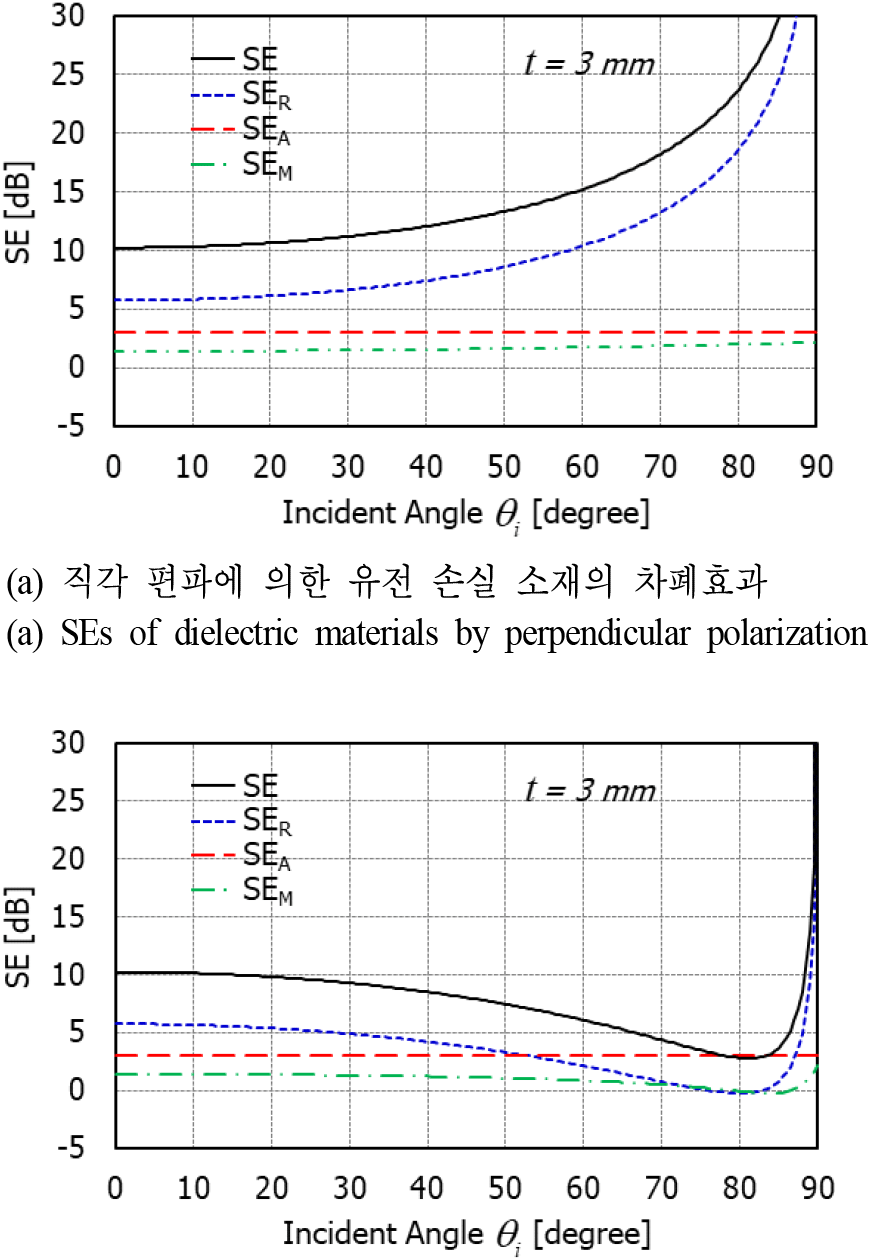
그림 5에서 그림 8까지는 유전 및 자성 흡수 소재들의 비스듬히 입사하는 두 편파에 의한 SE를 Schelkunoff가 정의한 반사손실(SE_R), 흡수손실(SE_A), 그리고 다중반사손실(SE_M) 성분으로 나누어 나타내었다. 소재의 두께에 따른 각 손실의 변화를 비교하기 위해서 3 mm와 30 mm 두 경우에 대해서 계산하였다. 그림 5는 3 mm 두께의 유전 흡수 소재의 3 GHz에서 SE를 보여준다. 직각 편파의 경우 반사손실이 흡수손실에 비해 크며, 따라서 SE는 주로 반사손실에 의해서 결정됨을 알 수 있다. 흡수손실은 입사 각도에 상관없이 일정함을 알 수 있다. 평행 편파의 경우에도 입사 각도에 대한 SE의 변화는 주로 반사손실의 변화와 일치한다. 50°C 이상의 입사 각도에서는 반사손실이 일정한 크기의 흡수손실에 비해 더 작아진다. 다중반사손실은 반사와 흡수손실에 비해 작음을 알 수 있다.

그림 5. | Fig. 5. 두께가 3 mm인 유전 손실 소재의 차폐효과 비교 | Comparison of SEs of dielectric material (LS26) with 3 mm thickness (f=3 GHz).

Download Original Figure

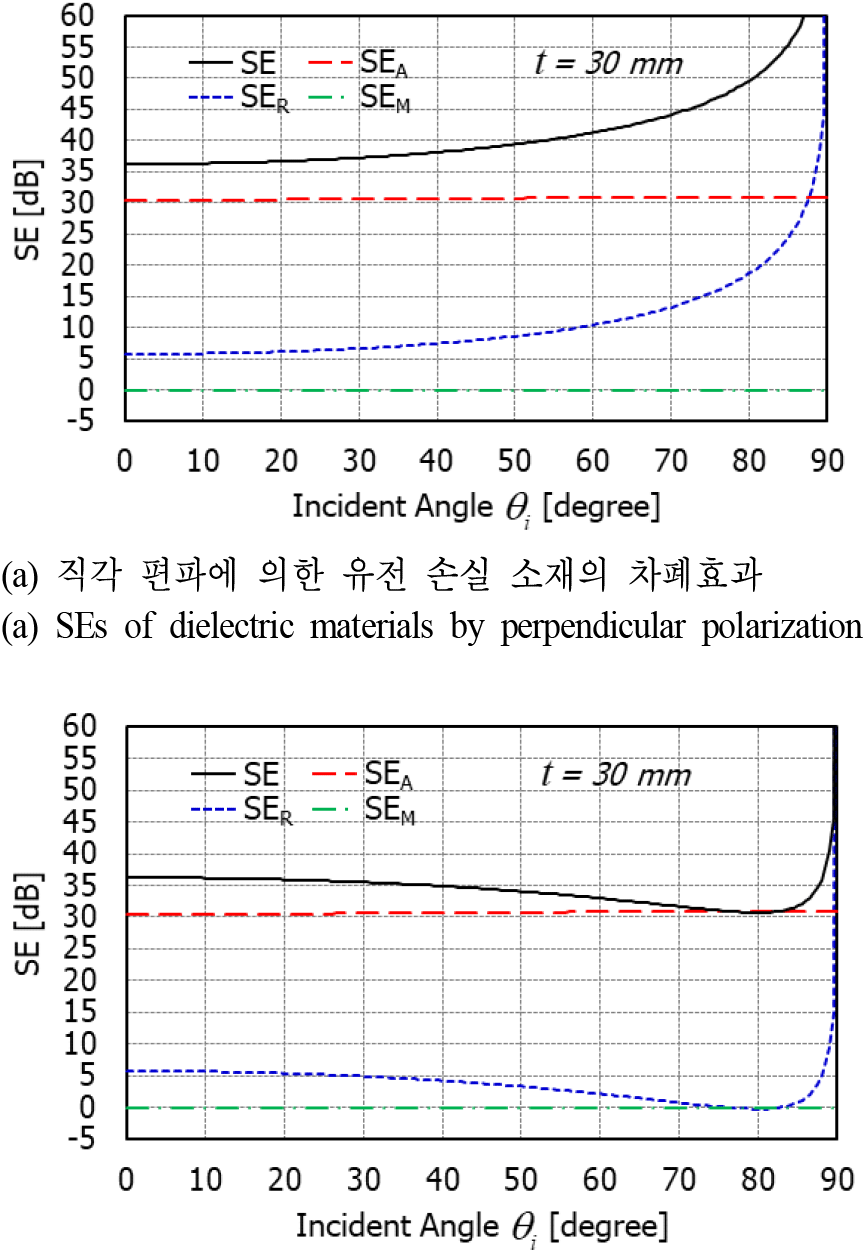
그림 6에서는 30 mm 두께의 유전 흡수 소재의 3 GHz에서 SE를 보여준다. 그림 5와 비교하였을 때 가장 큰 차이점은 입사 편파와 상관없이 소재의 두께가 10배 증감함에 따라 소재 내의 흡수손실이 약 3 dB에서 30 dB로 10배 증가하였다는 것이다. 이는 흡수손실(SE_A)의 정의에서 보듯이 흡수손실(SE_A)은 두께에 비례하기 때문이다. 또한 반사손실은 두께와 무관함을 알 수 있다. 흡수손실의 증가로 인해 다중반사손실은 더 작아졌다. 결과적으로 30 mm 두께의 유전 흡수 소재의 경우에 SE가 직각 편파일 때는 35 dB 이상으로, 평행 편파일 때는 30-36 dB 정도로 증가하였다.

그림 6. | Fig. 6. 두께가 30 mm인 유전 손실 소재의 차폐효과 비교 | Comparison of SEs of dielectric material (LS26) with 30 mm thickness (f=3 GHz).

Download Original Figure

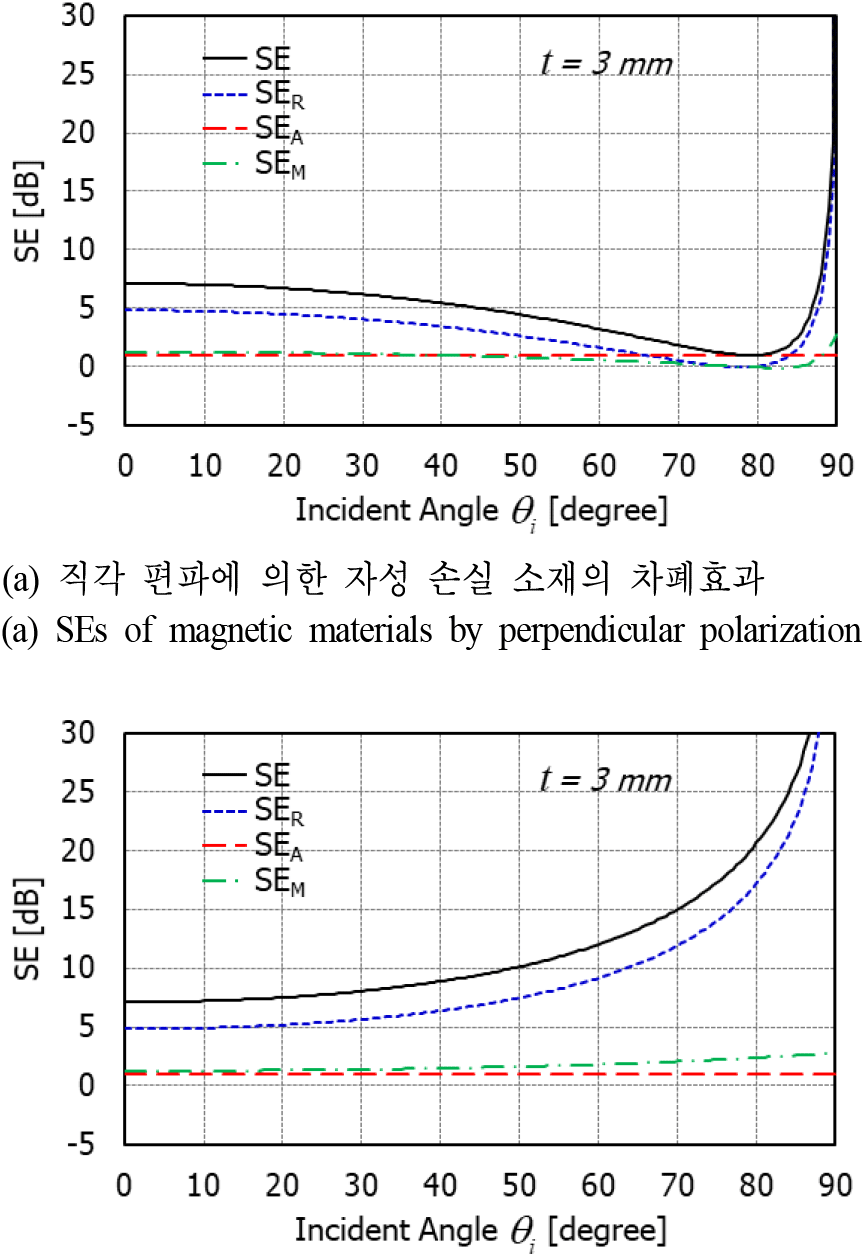
그림 7 및 그림 8에서는 각각 3 mm 두께와 30 mm 두께를 갖는 자성 흡수 소재의 반사손실, 흡수손실, 다중반사손실의 변화를 보여준다. 앞서 설명하였듯이 자성 흡수 소재는 입사 각도가 증가함에 따라 평행 편파의 SE는 증가하는 반면, 직각 편파의 SE는 감소하다가 80°C 이상의 입사 각도에서 급격히 증가한다. 그림 7에서 두께가 3 mm인 자성 흡수 소재의 SE는 주로 반사손실에 의해서 결정되며, 흡수손실은 1 dB 정도의 매우 낮은 값을 가진다. 다중반사손실의 경우 평행 편파에서는 입사 각도에 따라 약간씩 증가하며, 직각 편파에서는 줄어든다. 그림 7(a)에서 보듯이, 3 mm 두께의 자성 흡수 소재의 경우 78°C의 각도를 가지는 평행 편파가 입사할 경우 반사손실이 매우 낮아 거의 전투과 특성을 가짐을 알 수 있다.

그림 7. | Fig. 7. 두께가 3 mm인 자성 손실 소재의 차폐효과 비교 | Comparison of SEs of magnetic material (FSA300) with 3 mm thickness (f=3 GHz).

Download Original Figure

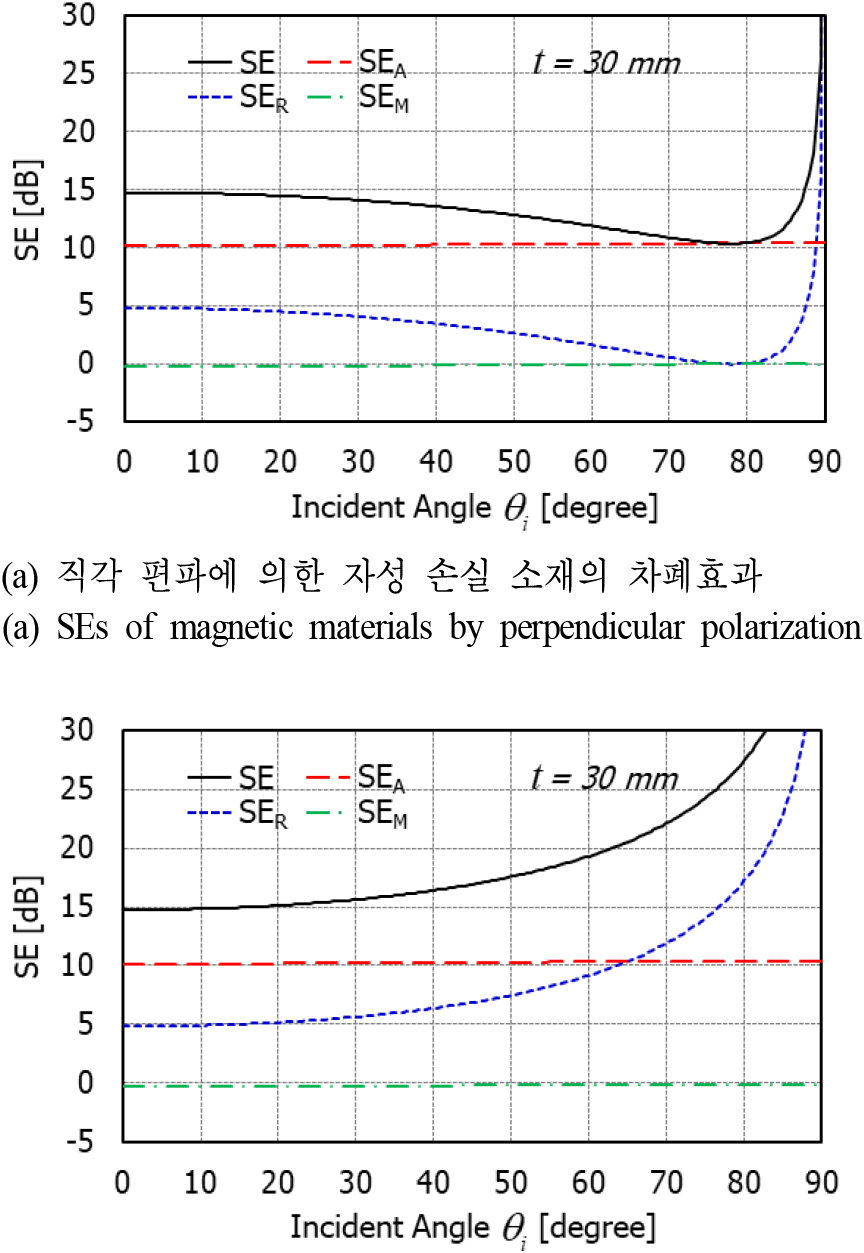
그림 8. | Fig. 8. 두께가 30 mm인 자성 손실 소재의 차폐효과 비교 | Comparison of SEs of magnetic material (FSA300) with 30 mm thickness (f=3 GHz).

Download Original Figure

그림 8에서는 30 mm 자성 흡수 소재의 SE를 보여준다. 유전 흡수 소재와 동일하게 두께가 10배 증가함에 따라 흡수손실도 10배 증가하여, 3 mm 두께의 소재에 비해 SE가 약 8 dB 증가하였다. 반사손실은 두께에 상관없이 동일하며, 다중반사손실은 흡수손실의 증가로 매우 작아졌다.

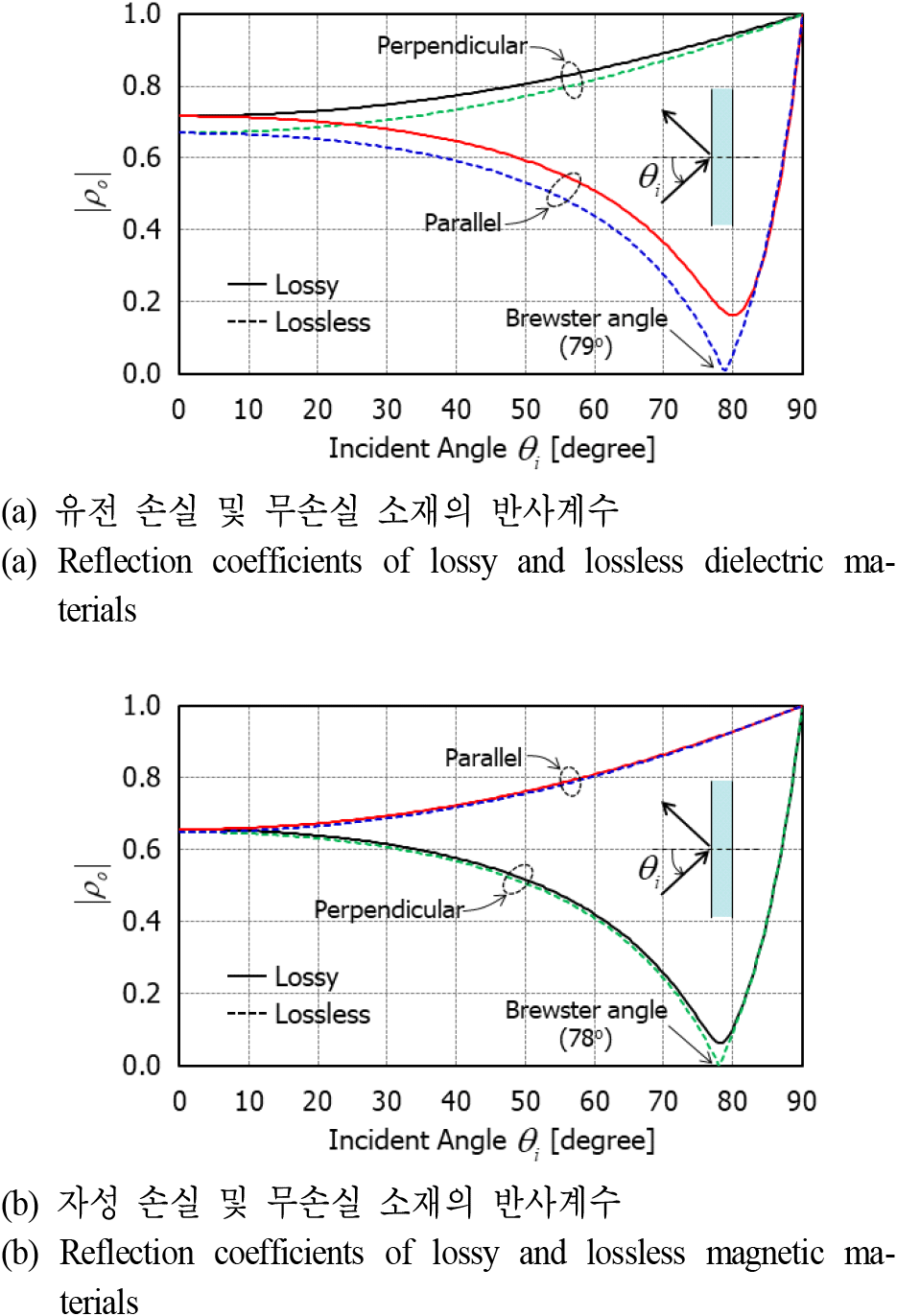
마지막으로 그림 9에서는 유전 및 자성 소재의 입사 각도에 대한 3 GHz에서의 반사계수를 보여준다. 특히 유전 및 자성 소재의 비유전율과 비투자율의 허수 성분을 0으로 놓은 무손실 유전 및 자성 소재의 반사계수도 비교하였다. 유전 무손실 소재의 경우 79°C의 평행 편파에서 그리고 자성 무손실 소재의 경우에는 78°C의 직각 편파에서 반사계수가 0이 되는 브루스터(Brewster) 각이 형성된다. 손실이 있는 유전 및 자성 소재에서는 브루스터 각이 존재하지 않지만 브루스터 각보다 약간 높은 입사 각도에서 가장 낮은 반사계수를 가짐을 알 수 있다. 이는 유전 손실 소재의 경우 그림 5(b) 및 그림 6(b)의 평행 편파 시 SE 결과에서, 그리고 자성 손실 소재의 경우 그림 7(a)와 그림 8(a)의 직각 편파 시 SE 결과에서, SE_R이 약 80°C에서 거의 0 dB로 감소하는 것과 동일한 현상이다.

그림 9. | Fig. 9. 입사 각도에 따른 손실 및 무손실 소재의 반사계수 비교 | Comparison of reflection coefficient of lossy and lossless materials by incident angle (f=3 GHz).

Download Original Figure

Ⅳ. 결 론

본 논문에서는 비스듬히 입사하는 평면파를 직각 편파와 평행 편파로 나누어 평판형 손실 소재의 SE 이론식을 유도하였고 유전 및 자성 흡수(손실) 소재들에 대한 차폐 특성을 분석하였다. 다양한 입사 각도와 소재의 두께에 따른 Schelkunoff의 반사, 흡수, 다중반사손실을 비교하였다. 또한 3차원 수치해석을 통해 그 결과의 경향성이 일치함을 확인하였다.