Ⅰ. 서 론
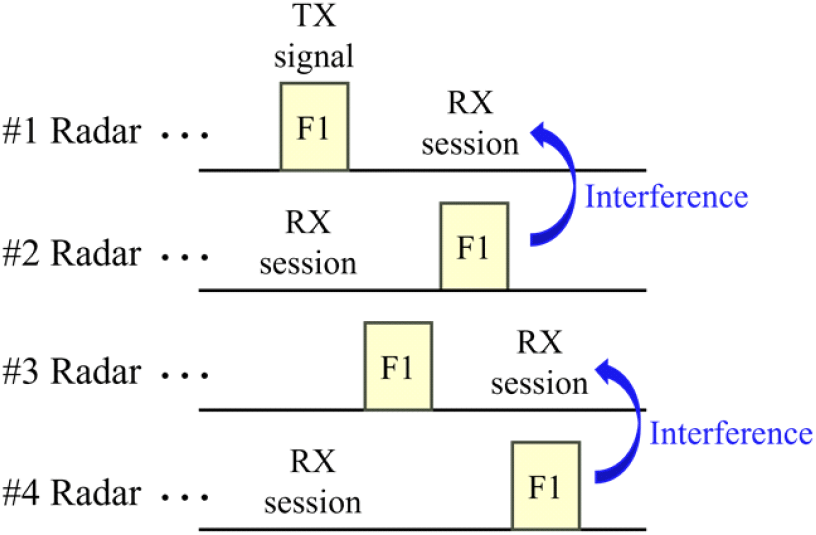
근접 방어 무기 체계(close-in weapon system)는 방공 시스템이 미사일 요격에 실패했을 때를 대비한 최후의 근거리 방어 수단이며, 주로 함정에서 사용되고 있다[1],[2]. 근접 방어 무기 체계에서 사용되는 레이다는 크게 탐색 레이다와 추적 레이다로 이루어진다[3]. 탐색 레이다는 다기능 레이다로서 근거리 및 중거리에서 미사일 탐지와 추적을 동시에 수행하고, 전 방향 탐지를 위해 4면으로 운용된다. 추적 레이다는 원거리에서 미사일 추적 기능을 수행한다. 이때, 탐색 레이다와 추적 레이다는 각각 X 대역과 Ku 대역으로 서로 다른 주파수 대역에서 운용된다. 각 레이다는 서로 근거리에서 동시 운용되므로, 높은 출력의 송신 신호는 인접한 레이다 면에 의해 수신되며, 간섭을 발생시킨다[4]. 그림 1은 레이다 면간 간섭이 발생하는 시나리오를 설명한다. 그림과 같이 4개 면의 레이다가 동시 운용될 때, 수신 구간의 레이다 면이 다른 레이다 면의 펄스 송신 신호를 원치 않게 수신하는 간섭이 발생한다. 이때, 수신되는 간섭 신호가 방향에 따라 다르게 합산됨에 따라 표적의 방향 모호성을 증가시키거나, 신호의 품질을 저하시켜 레이다의 탐지 및 추적 성능을 저하하는 원인이 되기 때문에[5],[6], 근접 방어 무기 체계의 레이다 운용을 위해서는 레이다의 면간 상호 간섭 분석 필요성이 제기된다.
이를 위해, 인접한 레이다의 안테나 소자 간 상호 결합(mutual coupling)을 분석하는 연구가 선행되었다[7],[8]. 또한, 인접한 안테나 및 탑재 구조체에 의한 패턴 왜곡 계수에 관한 연구도 진행된 바 있다[9]. 그러나, 기존 방식들은 인접한 레이다 및 탑재 구조체에 의한 상호 간섭을 정량적 지표로 나타낼 뿐, 간섭이 발생하는 방향에 대한 정보를 제공하지 못한다. 본 논문에서는 시뮬레이션 기반으로 해상에서 운용되는 근접 방어 무기 체계 레이다의 면간 간섭을 분석하는 방식을 제안하였다. 근접 방어 무기 체계와 같이 배열 안테나를 직접 모델링할 때 해석 mesh의 개수가 수백만 개가 넘어가는 경우, 시뮬레이션이 불가능하므로 해석 시간 단축이 목표가 되었다.
송신 안테나는 등가 near field source로 모델링하였으며, 간섭 신호를 수신하는 안테나는 동작 주파수에 따라 복소 필드 또는 복소 수신 전류로 분류하여 모델링하였다. 도출된 복소수 값을 기반으로 고각과 방위각에 대한 array manifold를 생성하여 수신 레이다 면에서 최대 간섭이 발생하는 방향과 그 방향에서의 전력 및 전류 세기를 도출하였다. 그리고, LOS(line-of-sight) 및 NLOS(non-light-of-sight)에 따른 면간 간섭 결과를 비교하였으며, 탑재 구조체에 의한 영향성을 조사하였다.
Ⅱ. 레이다의 면간 간섭 분석 방법
그림 2는 서로 다른 두 레이다 면이 각각 송신, 수신의 기능을 수행하는 경우, 레이다 면간 간섭을 분석하는 과정을 보여준다. 이때 레이다 면이란 배열 안테나가 탑재되는 레이다 개구면을 의미하며, 면간 간섭이란 레이다에서 송신된 신호가 인접한 타 레이다의 개구면을 통해 원치 않게 수신되는 전자기적 간섭을 의미한다.
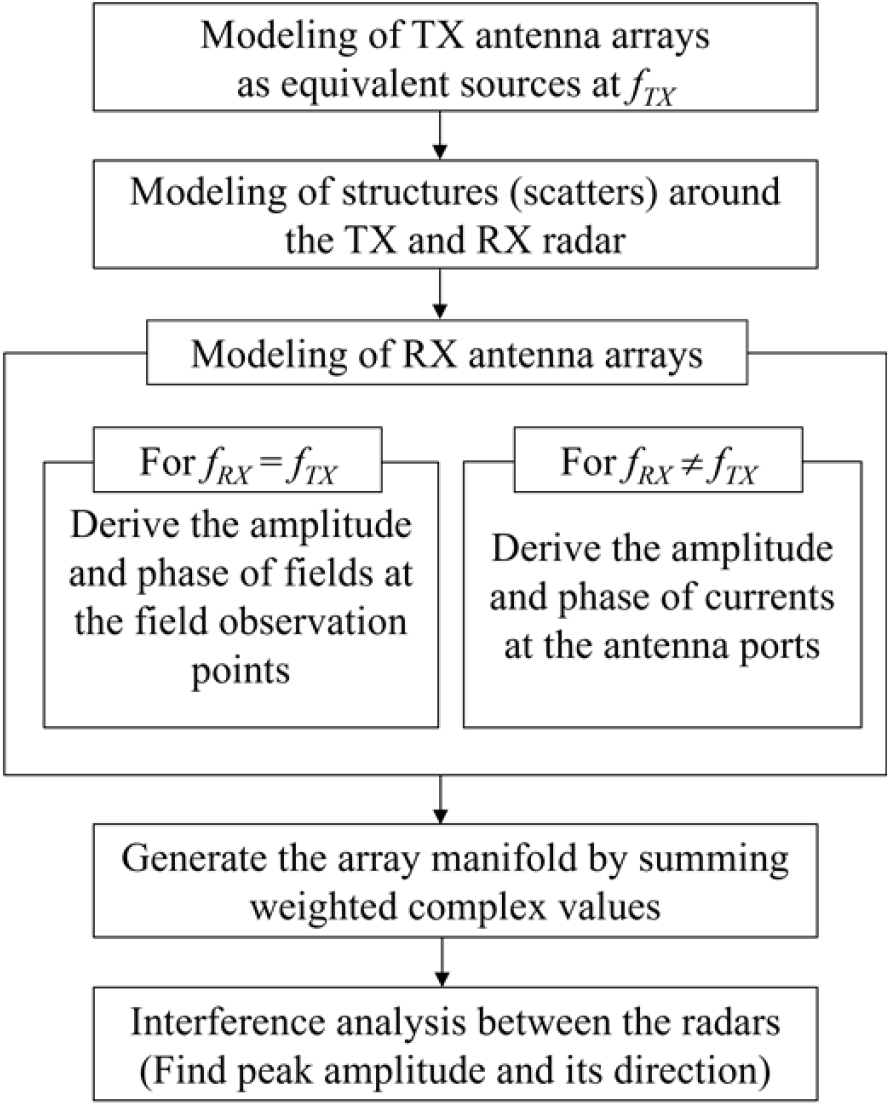
근접 방어 무기 체계에서 송신 레이다는 수백 개의 안테나로 이루어지며, 모든 안테나 소자를 설계하고 해석하는 방식은 많은 계산 시간과 자원을 요구한다. 따라서 본 연구에서는 equivalance theorem에 근거하여 송신 레이다를 안테나 소자와 동일한 전자기적 특성을 갖는 near field source로 모델링하였다[10]. 전자기적 해석 시뮬레이션 소프트웨어로는 FEKO가 사용되었으며, MLFMM(multi-level fast multipole method) 방식으로 해석을 실시하였다. Near field source 모델링 시, 전체 배열 안테나 소자에 요구되는 1,075,360개의 mesh 계산을 줄일 수 있어 해석 시간 단축이 가능하다. 다음으로는 실제 운용 시나리오를 가정하여 레이다 부근의 탑재 구조체를 모델링하였으며, 해석 시간 단축을 위해 구조체를 간소화하였다.
간섭 신호를 수신(RX)하는 레이다는 다음과 같이 모델링된다. 탐색(송신)-탐색(수신) 레이다의 경우처럼 송신(TX) 레이다의 운용 주파수(fTX)와 수신 레이다의 운용 주파수(fRX)가 같은 경우, FEKO의 point 할당 기능[11]을 통해 수신 레이다 각각의 안테나 소자를 field observation point로 설정하여 각 point에 인가된 필드 정보를 도출한다. MLFMM 해석 과정[12]에서, 필드 정보가 도출되는 과정은 다음과 같다. 먼저, TX 안테나가 등가 모델링된 near field source는 전류 밀도 J를 가진다. 전류 밀도는 source가 위치한 point 에서의 전기장을 생성한다. Field observation point에서의 potential은 방사체 위치로부터 공간상 임의의 지점에 유기된 field를 계산하는 Green function[13]을 통해 계산된다. 결과적으로 수신 레이다 면에서의 필드 정보가 도출되며, 탑재 구조체에 의한 scattering field 또한 합산되어 수신 레이다 면의 필드에 반영될 수 있다. 또한, 송신 신호 방향의 변화에 따른 수신 전자기장 값의 변화도 반영할 수 있다. 한편, 송신 레이다와 수신 레이다는 서로 원역장 영역에 존재하기 때문에, 수신 레이다의 개구면에 위치하는 field observation point로부터 도출된 필드 정보는 송신 레이다의 원역장 값인 동시에 수신 레이다의 근역장 값이 된다.
반면, 추적(송신)-탐색(수신) 레이다 경우처럼 fTX와 fRX가 서로 다른 경우, 시뮬레이션 해석 주파수가 fTX이므로 이는 수신 안테나의 동작 주파수가 아니기 때문에, fTX와 fRX가 같은 경우에 비해 수신 전력이 작게 된다. MLFMM 기법은 단일 해석 주파수에서 해석이 진행되기 때문에 field observation point로부터 수신하는 E-, H-field는 이런 특성을 반영할 수 없다. 따라서, fTX와 fRX가 다른 경우에는, 안테나 이득 특성을 반영할 수 있도록 수신 안테나 모델을 탑재하였으며, 각 안테나 포트에 유도된 복소 수신 전류를 도출한다. 그리고 도출된 복소수 값을 가중치 합산하여 임의의 간섭 신호 입사 방향에 대한 array manifold를 생성한다.
Array manifold는 방위각(ϕ)과 고각(θ) 방향으로 빔조향을 할 때 요구되는 steering vector를 포함하는 행렬을 의미하며, 각 방향에서의 간섭 세기를 나타내기 위한 2차원 table로서 도입된다. 이때, 각 안테나 위치에 해당하는 복소 필드 또는 복소 전류 값들에 해당 방향의 steering vector가 인가되어 합산된 뒤 array manifold의 element가 된다. 생성된 array manifold를 통해 수신 레이다 면에서 최대 간섭이 발생하는 방향과 그 방향에서의 전력 및 전류 세기를 도출한다.
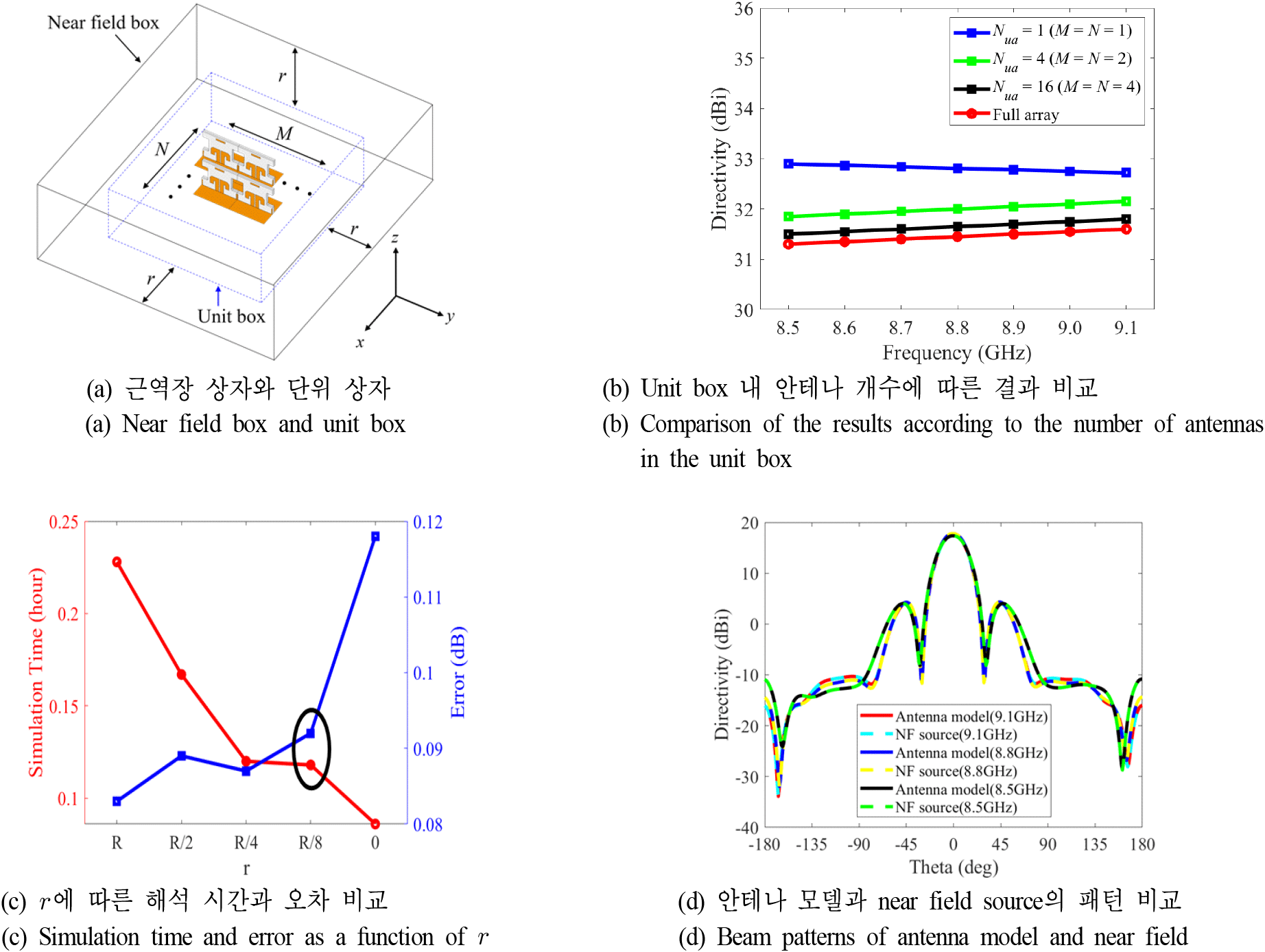
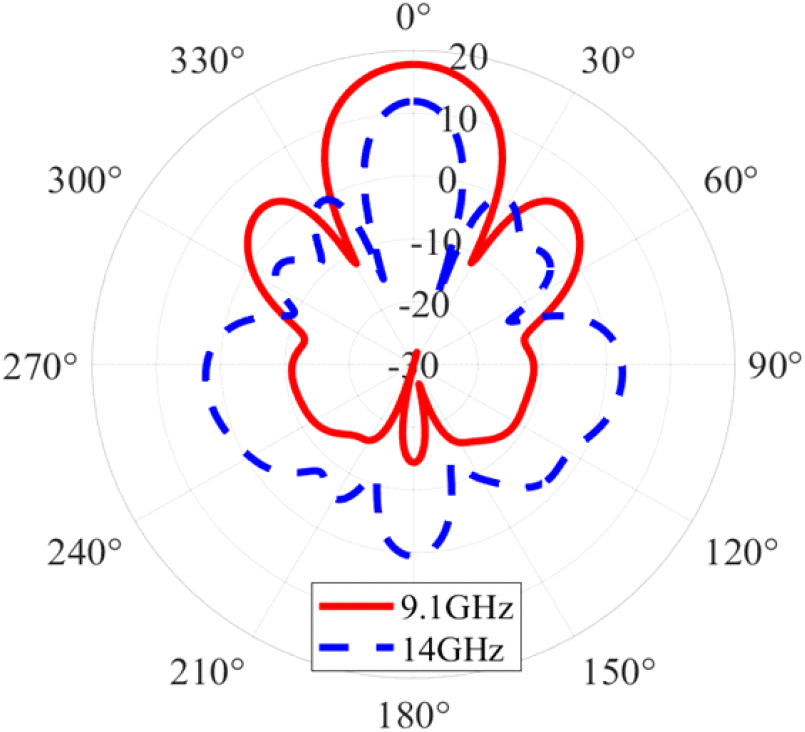
Equivalent theorem에 근거하면, 전자기장을 방사하는 안테나 모델과 동일한 특성을 갖는 등가 source 생성이 가능하다. 본 연구에서는 등가 source로서 near field를 사용하였다. 보다 정확한 near field source를 생성하기 위해서는 배열 안테나 간 커플링이 충분히 고려될 수 있는 최소 안테나 개수 및 해석에 사용되는 near field box의 크기가 중요한 조건이 된다. 그림 3(a)는 요구되는 조건을 도출하기 위한 near field box와 unit box를 보여준다. Unit box는 M × N 배열의 인쇄형 다이폴 안테나를 포함하며, 안테나 배열과 동일한 크기를 갖는다. Near field box는 unit box보다 x, y, z-축 방향으로 거리 r만큼 더 크며, near field source가 해석되는 실제 box이다. Unit box 내 안테나 개수는 Nua로 정의되며, 정확한 해석에 필요한 최소의 N_ua를 도출한다. 그리고, 도출된 최소 단위의 N_ua를 기반으로 전체 배열 안테나의 성능을 예측한다. 그림 3(b)는 X 대역에서 Nua에 따른 전면 방향에서의 directivity를 비교한 결과를 보여준다. 단일 안테나(Nua=1)에 기반하여 배열 안테나 성능을 예측하는 경우, 안테나 간의 커플링이 고려되지 않아 실제 안테나 모델과 directivity 차이가 발생한다. Nua가 4, 16으로 증가함에 따라 그 차이가 줄어들게 되며, 특히 Nua=16일 때, 0.24 dB로 근소한 차이를 보이게 된다. 결과적으로 안테나 소자 16개를 전체 안테나 배열을 모사하기 위한 최소 단위로 설정하였다. 그림 3(c)는 near field box 크기를 결정하는 길이 r에 따른 시뮬레이션 시간과 오차를 나타낸다. R은 해석 주파수에서의 원역장 거리인 2D2/λ이며, 오차(error)는 실제 안테나 모델과 near field source를 이용한 모델 간의 최대 directivity 차이이다. 그림에서 r이 감소함에 따라 시뮬레이션 시간은 감소하는 반면, 오차는 증가하는 경향을 확인할 수 있다. 시뮬레이션 시간과 오차를 모두 고려하여 r=R/8로 설정하였다. 그림 3(d)는 실제 안테나 모델과 Nua=16, r=R/8인 near field source에 기반한 모델 간의 방사 패턴을 비교한 결과이다. X 대역에서 주파수에 상관없이 두 모델의 방사 패턴이 거의 동일함을 확인할 수 있다. 이로써 제안된 송신 레이다 안테나 해석 방식이 해석 시간을 단축하면서도 실제 안테나 모델과 거의 동일한 특성이 보임을 확인하였다.
해석을 통해 생성된 등가 source는 레이다의 배열 안테나 개수에 따라 그림 3(a)의 x, y 방향으로 각각 P, Q개 만큼 배열된다. 이때, x-축에서 p번째, y-축에서 q번째에 위치한 등가 source의 E-, H-field는 각각 Epq, Hpq로 표현된다. z-축에서 x-축 y-축 방향으로의 빔조향 각도 (θx, θy)에 따라 array factor를 E0, H0 값에 적용함으로써 식 (1) 및 식 (2)의 Epq,Hpq를 정의할 수 있고 빔조향시 레이다 면간 간섭을 분석할 수 있다.
Epq, Hpq : E-field and H-field of NF source at (p,q)
where 1≤p≤P, 1≤q≤Q
E0, H0: E-field and H-field of NF source at (1,1)
dx, dy: Distance between two adjacent NF sources in x,y direction
θx, θy : Steering angle in x,y direction.
송신 레이다로부터 발생하는 간섭 신호를 수신하는 레이다의 배열 안테나는 그림 4처럼 field observation point 또는 복소 수신 전류로 등가 모델링된다. 송신 레이다와 수신 레이다가 동일한 운용 주파수를 갖는 경우, 수신 레이다의 안테나는 field observation point로 모델링된다. 이때, 각 point 간 배열 간격은 실제 배열 안테나와 동일하며, field observation point에서 레이다의 면간 간섭에 의한 복소 필드 정보를 도출한다.
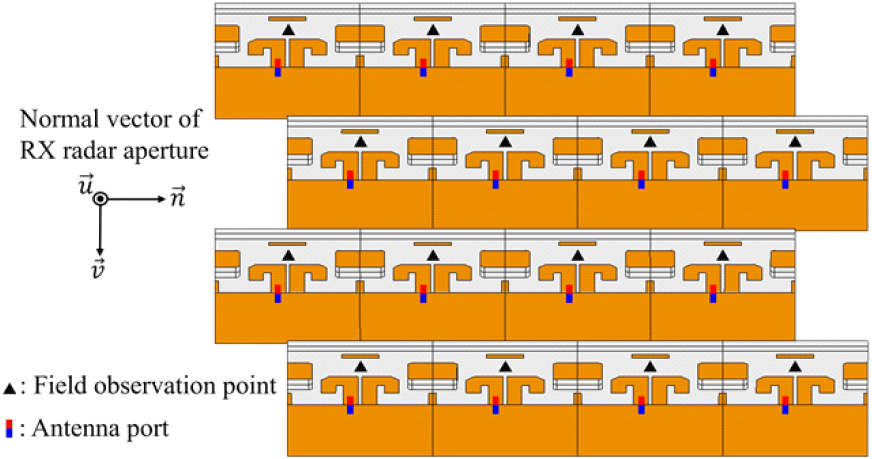
한편, 이러한 필드 도출은 같은 해석 주파수에서만 유효하므로, 송신 레이다와 수신 레이다의 운용 주파수가 서로 다른 경우에는 대신에 안테나 포트에 유도되는 복소 수신 전류를 도출한다. 그림과 같이 포트는 각 안테나 소자의 급전부에 위치하며, 50-Ω으로 단락되어 있다. 그림 5는 해석 주파수에 따른 수신 안테나의 이득 패턴을 나타낸다. 해석 주파수가 수신 안테나 운용 주파수일 경우, 수신 안테나 전면 방향 이득은 17.78 dB이나, 송신 안테나 운용 주파수일 경우 안테나 이득은 11.91 dB로, 약 5.87 dB의 차이가 발생한다. 안테나의 상호 법칙에 의해 안테나가 송·수신할 때 이득과 같은 전기적 특성은 동일하다. 이는 수신 안테나의 이득 감소가 곧 안테나의 개별 포트로부터 수신되는 신호 세기 감소의 원인이 됨을 의미한다. 따라서, 위와 같은 안테나의 이득 특성을 반영하기 위해 안테나 모델을 설계하였다.
수신 레이다 위치에는 uvn 지역 좌표계가 도입되어 면간 간섭의 방향을 수신 레이다 개구면 기준으로 표현할 수 있다. uvn 좌표계는 레이다 개구면에 수직인 법선 벡터가 와 개구면을 이루는 으로 구성된다. 이를 통해 수신 레이다에 입사되는 신호 방향을 (ϕlocal, θlocal)로 표현할 수 있다.
uvn 좌표계에 위치한 원점과 임의의 좌표(u0, v0, n0)가 있을 때, ϕlocal와 θlocal는 식 (3) 및 식 (4)와 같이 정의된다. ϕlocal은 입사 신호를 uv-평면에 사영(projection)시켰을 때 u-축과 이루는 각도이고, θlocal은 입사 신호를 un-평면에 사영시켰을 때 n-축과 이루는 각도이다.
식 (5) 및 식 (6)은 해석을 통해 도출된 복소 필드이며, 식 (7)은 수신 전류를 나타낸다. Ei와 Hi는 i-th field observation point의 E-field, H-field로, uvn-축에 대한 vector이며, 복소수 값을 갖는다. Ii는 i-번째 안테나 포트의 수신 전류이며, 역시 복소수 값을 갖는다.
ψi: Phase difference at the i-th field observation point and antenna port.
τi: Time delay at the i-th field observation point and antenna port.
: Relative position vector of the field observation point and antenna port from (0, 0, 0) in uvn-coordinate.
입사되는 신호의 방향이 (ϕlocal, θlocal)일 때, ψi와 τi는 각각 i-번째 field observation point에서의 위상 차이와 시간 지연을 의미한다. 시간 지연에 의해 위상 차이가 발생하며, 식 (11)과 같이 τi는 단위 방향 벡터인 와 기준 field observation point (0, 0, 0)의 위치로부터 관찰하는 point의 상대적 위치에 따른 수신 거리 차이를 반영한다. 식(8) 및 식 (9)에서 모든 안테나 소자의 복소 필드 및 복소 수신 전류에 특정 방향에 대한 위상 차이 가중치를 인가해 준 뒤 합산하면 해당 방향에서의 간섭의 세기를 얻을 수 있다. 이때, 복소 필드의 전기장과 자기장으로부터 식 (10)의 포인팅 벡터를 도출한 뒤 전력을 계산하였다. K는 수신 배열 안테나의 총 개수로, field observation point 그리고 antenna port의 개수와 동일하다. 이때, K가 증가할수록, 개별 복소 필드 또는 수신 전류에 비해 위상 가중치의 영향성이 상대적으로 더 커지게 된다. 그러므로, 배열 소자가 많은 환경에서 제안된 방식을 통해 도출된 간섭 신호의 전력과 전류는 실제 full-wave simulation 해석 결과와 유사한 경향성을 갖게 된다. ϕlocal는 0°~360°, θlocal는 0°~180° 범위에서 1° 단위를 가지며, 최종적으로 2차원 array manifold 행렬을 생성하였다.
제안된 면간 간섭 분석 방식을 검증하기 위해 그림 6과 같이 LOS(line-of-sight)와 NLOS(non-line-of-sight) 환경으로 나누어 해석을 시행하였다. 본 분석에서는 레이다 부근의 탑재 구조체를 제외하였다.
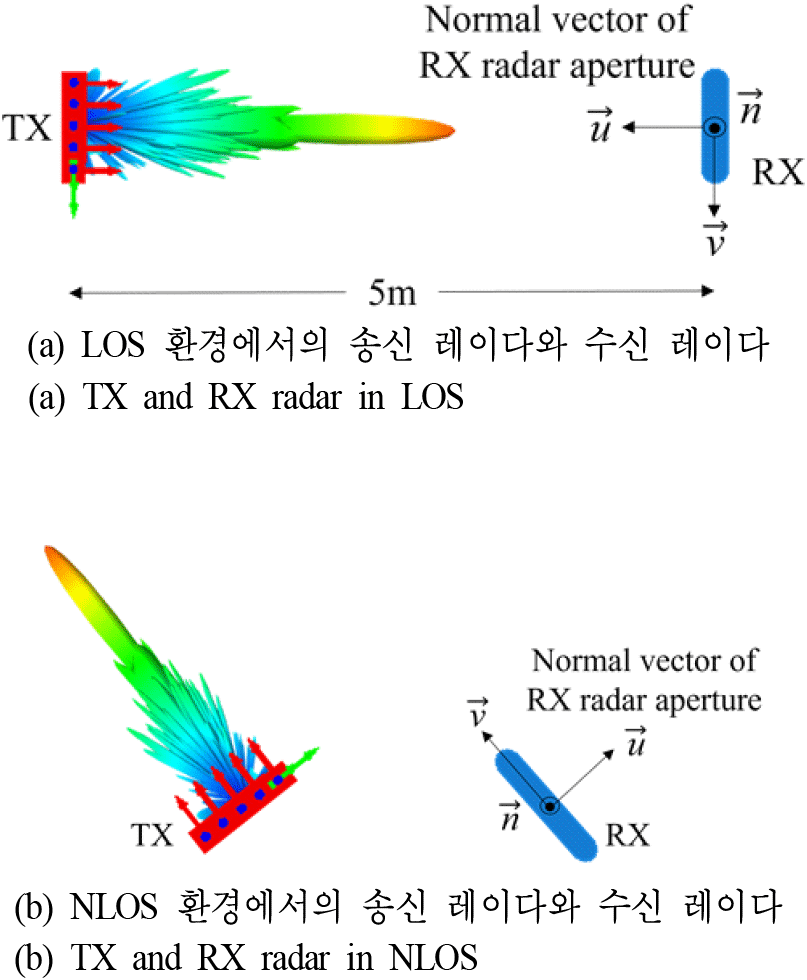
송신 레이다에는 공통으로 near field source (Nua=16)가 배열되어 있으며, 개구면과 수직한 전면 방향으로 지향성을 갖는다. 송신 레이다의 전체 입력 전력은 40 dBm으로 설정하였다. 수신 레이다는 송신 레이다의 원역장 영역에 위치하며, local 좌표계(uvn-좌표)를 갖는다.
그림 6(a)는 송신 레이다와 수신 레이다가 서로를 바라보는 LOS인 환경을 보여준다. 해당 경우에서는 수신 레이다에서 최대 간섭 방향은 전면 방향임을 쉽게 예측할 수 있다. 반면, 그림 6(b)는 송신 레이다와 수신 레이다가 서로 다른 방향을 바라보는 NLOS 환경을 보여준다. 송신 레이다가 전면 방향을 향해 빔조향하는 경우, 수신 레이다의 개구면을 기준으로 어떤 방향에서 높은 간섭이 발생하는지에 대한 분석이 필요하다.
그림 7은 송신 레이다와 수신 레이다의 운용 주파수가 X 대역으로 같을 때, 필드 정보로부터 생성된 2차원 array manifold의 결과를 나타낸다. 수신 레이다의 수신 유효범위는 −50°<ϕlocal<50°, 30°<θlocal<146°이므로 이 범위를 FOV(field of view)로 정의하였다. LOS 환경인 그림 6(a)의 결과는 그림 7(a)처럼, 송신빔이 입사하는 ϕlocal=0°, θlocal=90° 방향에서 최대 간섭을 보여주며, 이때의 세기는 1.569 W이다. NLOS 환경인 그림 6(b)의 결과는 그림 7(b)와 같이 레이다 FOV 범위 밖의 ϕlocal=65°, θlocal=62° 방향을 바라볼 때 0.845 mW의 크기로 최대 간섭이 발생한다는 것을 알 수 있다. 한편, 생성된 array manifold는 그림 7(a)의 ϕlocal=180°, θlocal=90°, 그림 7(b)의 ϕlocal=115°, θlocal=62°에서도 최댓값을 갖는 등 ϕlocal=90°에 대해서 대칭인 값을 갖는 것을 확인할 수 있다. 이러한 최대 간섭 방향의 대칭성이 존재하는 이유는 uvn-좌표계에서 모든 field observation point 및 안테나 포트가 ϕlocal=90° 평면에 위치하기 때문이다. 식 (9)의 τi 가 ϕlocal=90° 평면에 대칭인 서로 다른 두 unit 방향 벡터 에 대해 같은 값을 갖게 되고, 이것은 대칭인 두 방향에서 동일한 세기를 산출한다. 하지만, field observation point와 안테나 포트에 해당되는 수신 레이다의 개구면은 레이다 앞면에 존재하므로 −90° <ϕlocal<90° 범위가 실제 레이다의 수신 값이다.
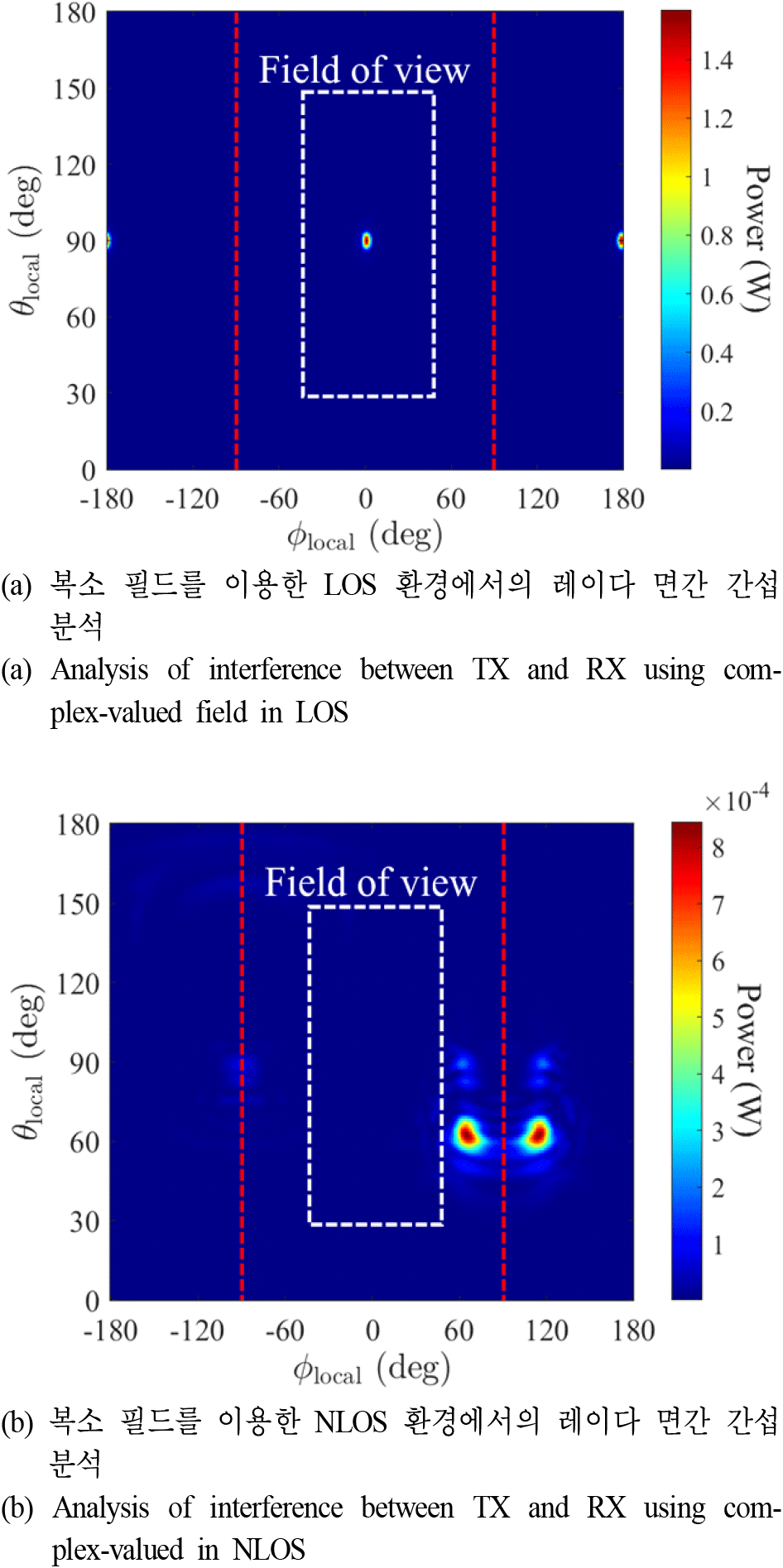
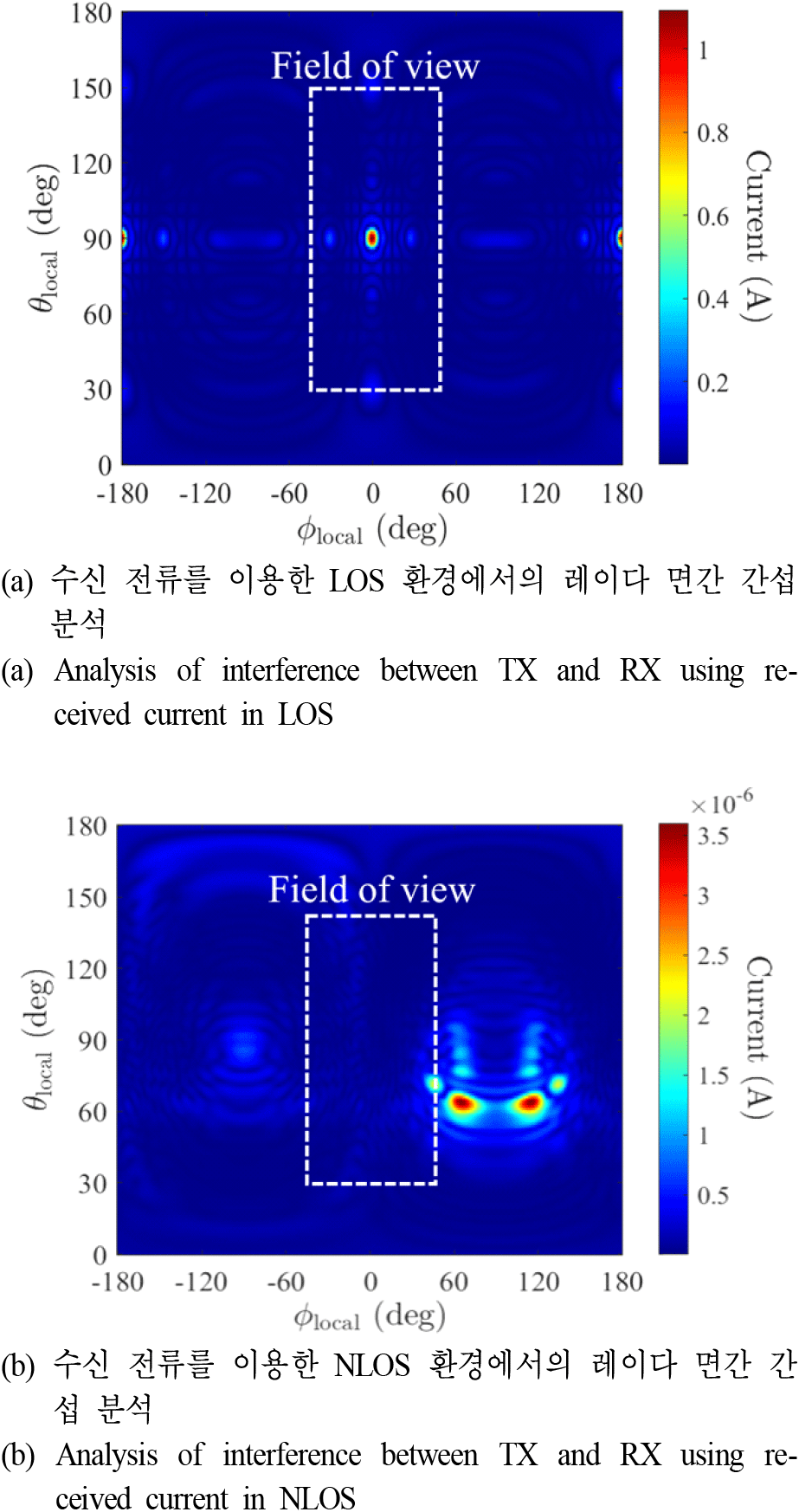
그림 8은 송신 레이다(Ku 대역)와 수신 레이다(X 대역)의 운용 주파수가 다를 때, 복소 수신 전류 정보로부터 생성된 2차원 array manifold의 결과를 나타낸다. 그림과 같이, 추출된 수신 전류 정보로부터 생성된 array manifold 결과는 LOS와 NLOS 환경에서 복소 필드 해석 결과와 거의 유사함을 확인할 수 있다. 이를 통해, 레이다 운용 주파수에 따라 빔 특성이 크게 변하지 않는다면, 복소 필드와 수신 전류 결과로부터 각각 생성된 array manifold는 유사함을 예측할 수 있다.
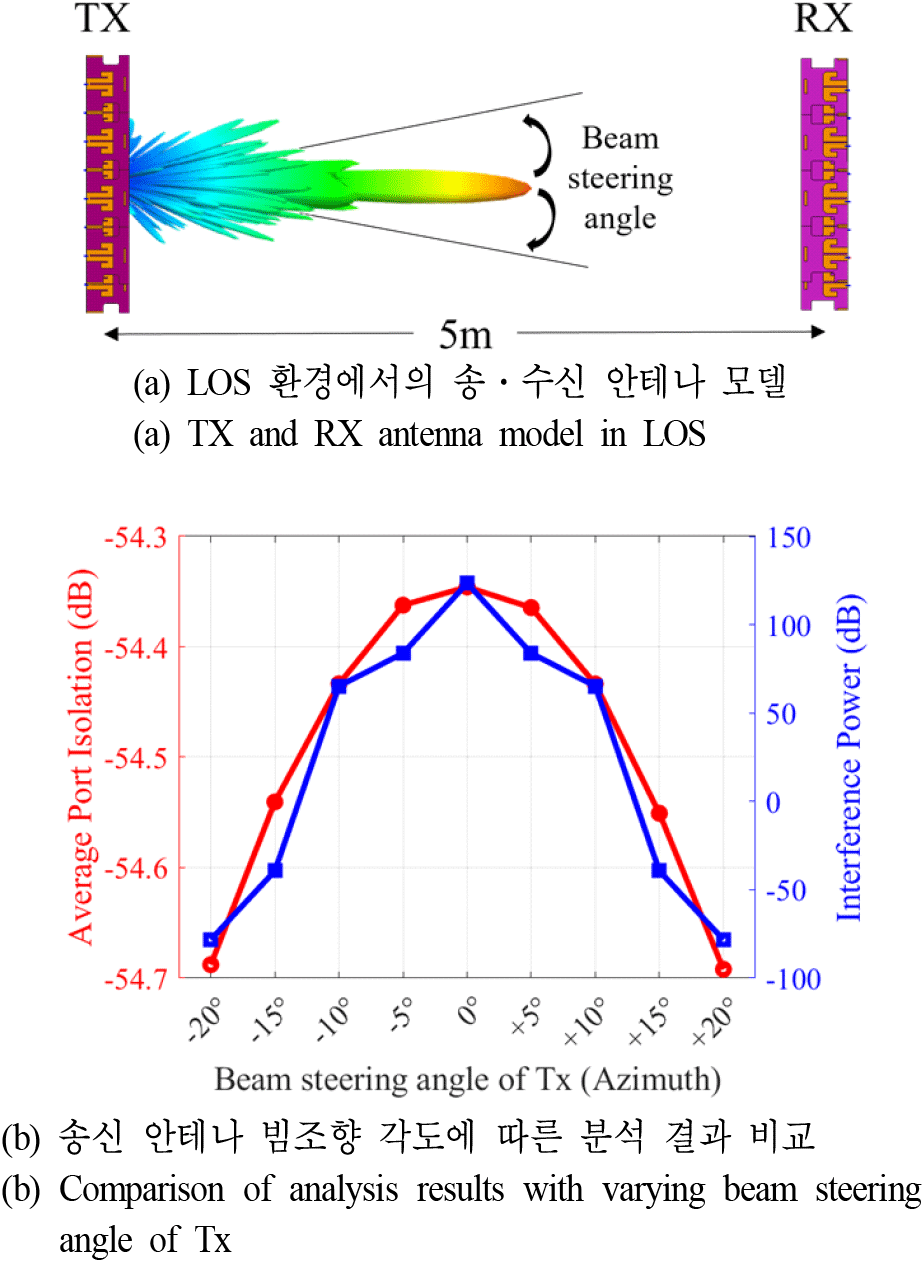
한편, 제안된 면간 간섭 분석 방법이 full-wave simulation 결과와 유사하다는 것을 검증하기 위해서, 통상적인 간섭 분석 기법인 안테나 소자 간 격리도(S-parameter)와 제안된 간섭 결과를 비교하였다. 그림 9(a)와 같이 LOS의 환경에서 TX와 RX 위치에 각각 4×4 배열의 추적안테나와 탐색안테나 모델을 탑재한다. 이후, TX 안테나의 개구면 방향을 RX가 위치한 방향으로부터 회전시키며, TX 안테나 포트와 RX 안테나 포트 상호 간의 S-parameter 값을 계산한다. 동일하게, 본 논문에서 제시된 방법을 적용해 송신 빔조향 방향을 회전시키며, RX 레이다 기준 면간 간섭의 세기를 측정한다. 그 결과, 그림 9(b)와 같이 빔조향 각도가 커져 전면 방향에서 벗어날수록, full-wave simulation 결과인 격리도가 점점 작아진다. 제안된 방법의 결과인 interference power 또한 빔조향 각도가 증가함에 따라 간섭 세기가 작아지게 되며, full-wave simulation 결과와 유사한 경향성을 가지는 것을 확인하였다.
Ⅲ. 제시된 방법을 이용한 간섭 분석
실제 운용 시나리오를 가정하여 제안된 분석 방법을 적용하기 위해 레이다 부근의 탑재 구조체를 모델링하였다. 그림 10에는 분석을 위해 모델링된 추적/탐색 레이다와 탑재 구조체 형상을 보여준다. 그림과 같이 가운데에는 상하 −20°~80° 회전이 가능한 포신과 함께 Ku 대역에서 운용되는 1개의 추적 레이다가 위치하며, 좌우로 포가 구조체와 함께 4개의 X 대역 탐색 레이다가 탑재된다. 이때, 추적 레이다의 입력 전력은 46 dBm, 탐색 레이다의 입력 전력은 40 dBm이다. 시뮬레이션 해석 시간 단축을 위해 탑재 구조체는 간소화하여 모델링하였다. 해당 분석에서 모든 레이다는 서로 NLOS인 상황이다.
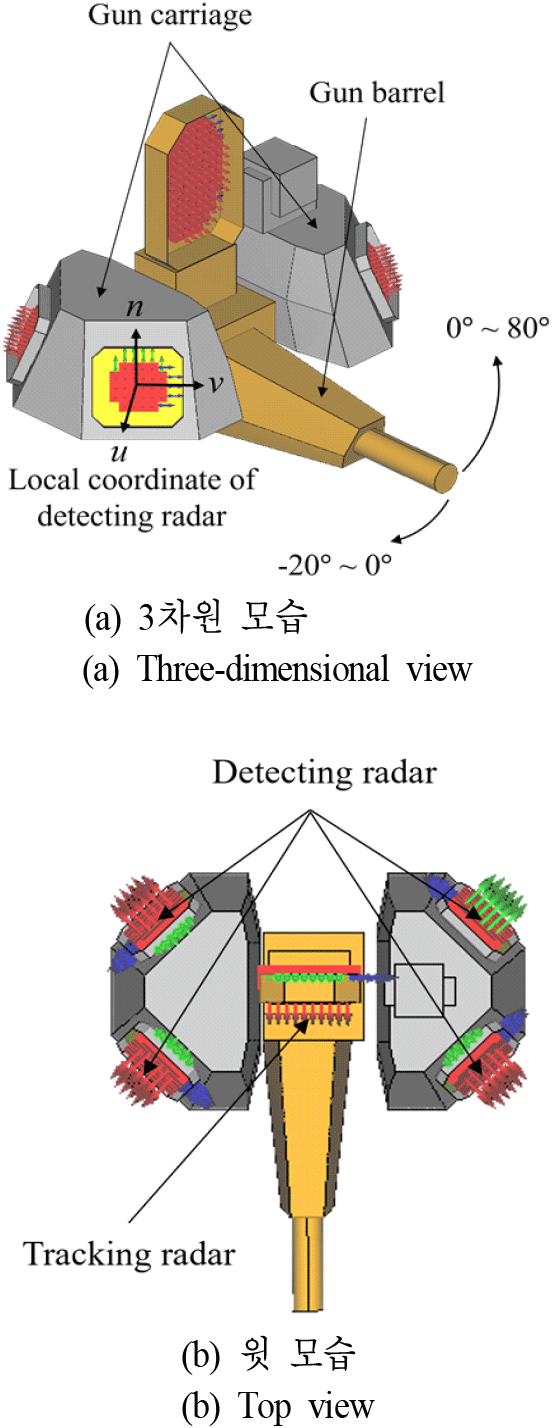
그림 11(a)는 레이다가 모델링된 탑재 구조체와 함께 있는 경우의 간섭 분석을 위한 송·수신 레이다 위치를 나타낸다. 그림 11(b)에서 그림 11(a)의 탐색 레이다가 +x-축 방향으로 빔조향하는 경우 반대편 탐색 레이다에 입사되는 간섭 세기를 array manifold로 나타내었다. 이 경우, 송·수신 레이다의 운용 주파수가 같으므로 복소 필드 정보를 활용하였으며, FOV 내에서 면간 간섭이 미약함을 확인하였다. 또한, FOV 범위 밖의 ϕlocal=−85°, θlocal=102° 방향을 바라볼 때, 6.152 μW의 크기로 최대 간섭이 발생한다는 것을 알 수 있다.
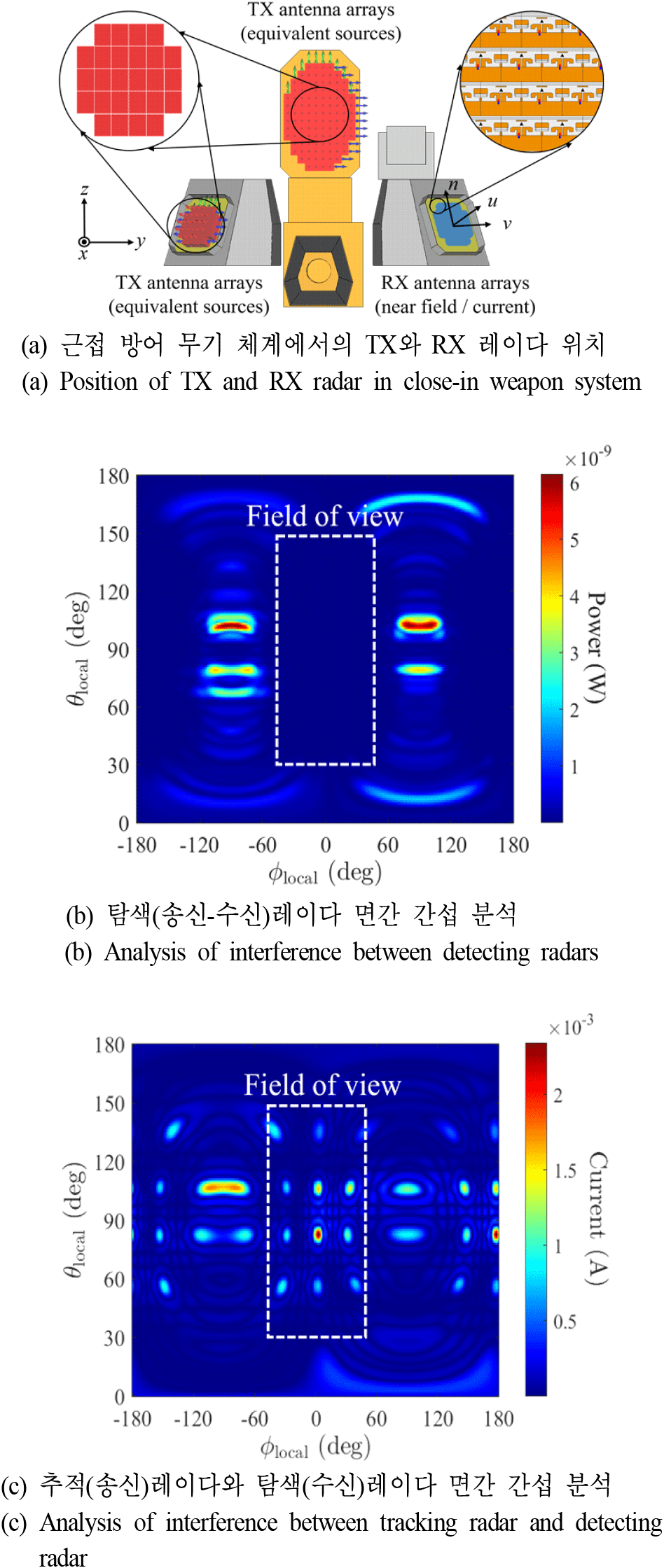
그림 11(c)는 서로 다른 운용 주파수를 가진 레이다의 면간 간섭 분석 결과이다. 그림 11(a)에서 추적 레이다(Ku 대역)가 xyz-좌표계에서 방위각 15°, 고각 −15° 방향으로 신호를 송신할 때, 탐색 레이다(X 대역)가 받는 간섭 영향성을 분석하였다. 동작 주파수가 다르므로 복소 수신 전류 정보를 분석에 활용하였으며, FOV 내에서의 평균값은 0.105×10−3 A로 확인되었다. 또한 FOV 내에서 가장 높은 간섭의 방향은 ϕlocal=3°, θlocal=83°이며, 간섭 신호로 생성된 전류의 크기는 2.344×10−3 A로 확인되었다.
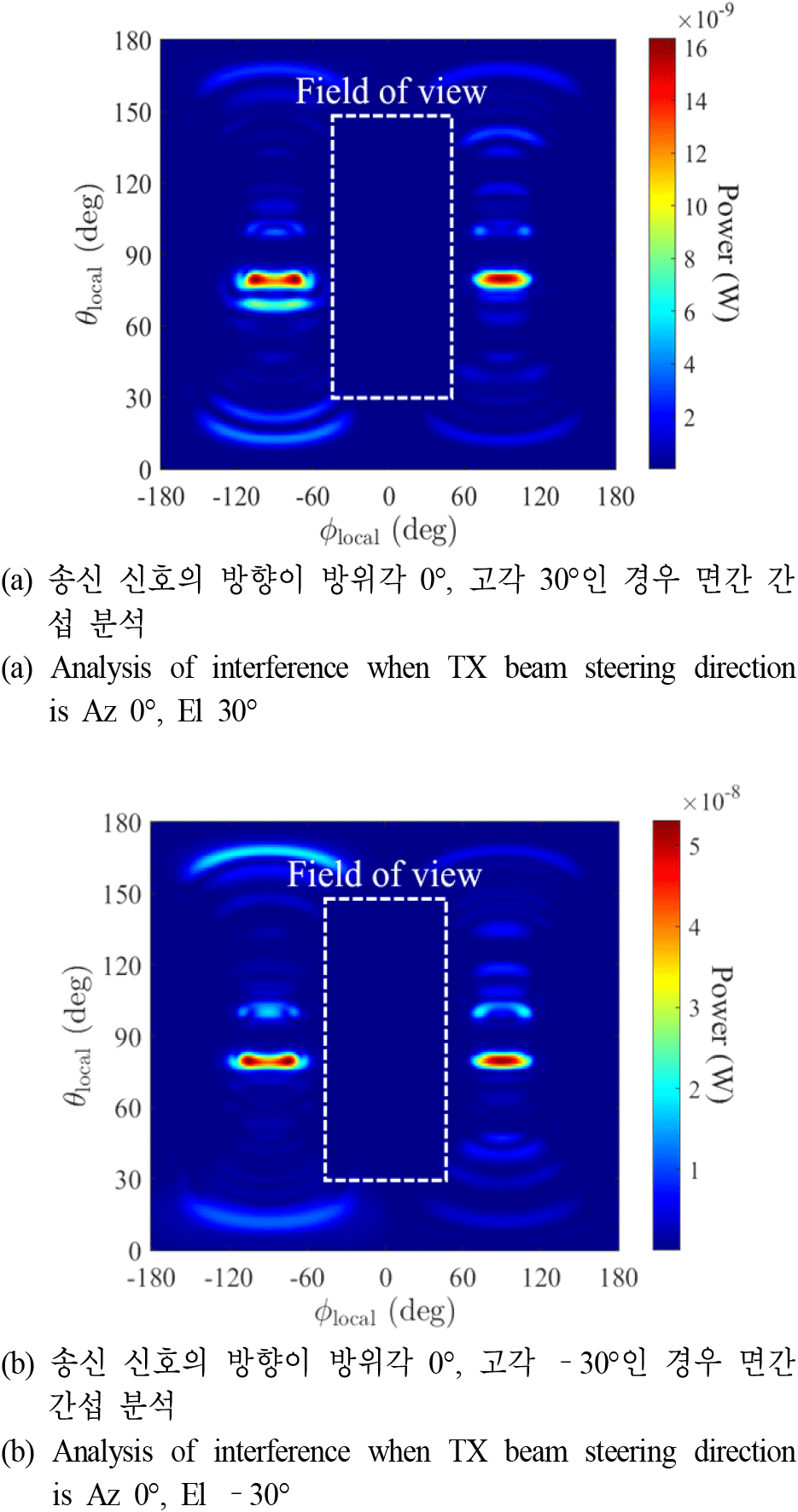
송신 신호의 방향이 바뀌는 경우, 간섭 분석 결과의 변화를 파악하기 위해 그림 11(b)의 시뮬레이션 상황을 이용하였다. 기존 송신 빔이 xyz-좌표계에서 방위각 0°, 고각 0° 방향이었다면, 방위각 0°, 고각 ±30°로 바뀔 시 간섭에 대한 결과가 각각 그림 12(a)와 그림 12(b)에 제시된다. 두 경우 모두 FOV 내에서 면간 간섭은 매우 미약함을 확인하였으며, 그림 12(a)의 경우 ϕlocal=−74°, θlocal=80° 방향에서 16.365 μW의 크기로, 그림 12(b)의 경우 ϕlocal= −75°, θlocal=79° 방향에서 53.117 μW의 크기로 최대 간섭이 발생한다는 것을 확인하였다. 결과적으로 제안된 레이다의 면간 간섭 분석 방식은 LOS뿐만 아니라, NLOS 상황에서도 유효하며, 탑재 구조체의 영향을 반영할 수 있음을 검증하였다.
Ⅳ. 결 론
근접 방어 무기 체계에 사용되는 레이다는 근거리에 위치하고, 강한 출력으로 동작하므로 인접한 레이다 면에 간섭을 발생시켜 레이다 성능을 저하한다. 본 논문에서는 레이다의 면간 간섭 분석 방식을 제안하였다. 해석 시간 단축을 위해 송신 레이다 안테나 모델과 동일한 성능을 가지는 near field source를 도출하였다. 또한, 수신 레이다의 배열 안테나는 송신 레이다와의 운용 주파수 차이에 따라 복소 필드 또는 복소 수신 전류로 등가 모델링하였다. 복소 값 형태의 필드가 수신 전류에 방향 가중치를 인가해 줌으로써 각 방향에서의 간섭의 세기를 분석하는 array manifold 행렬을 생성하였다. 제안된 분석 방식을 검증하기 위해 LOS와 NLOS 상황에서 레이다 시뮬레이션 해석을 진행하였으며, 최대 간섭이 발생하는 방향과 세기를 확인하였다. 또한, 실제 레이다 운용 시나리오를 가정해 레이다 주변에 탑재 구조체가 적용된 상황에서 면간 간섭 분석을 진행하였다. 결과적으로, 제안된 방식은 근접 방어 무기 체계의 운용 시나리오에 적용하여 레이다 면간 간섭 분석에 활용될 수 있음을 확인하였다. 해당 기술은 다양한 산업 분야에서 다중 레이다 간 간섭 분석 방식으로 활용될 수 있을 것으로 기대된다.