Ⅰ. 서 론
일반적으로 SAR(synthetic aperture radar) 영상은 주/야간 및 기상 조건과 관계없이 관측 영역의 영상 정보를 획득할 수 있는 장점이 있어 민간 및 군사 분야에서 널리 활용된다. 그러나 최근 이론 연구와 실제 사례에서는 전파 간섭이 SAR 영상을 왜곡하고 표적 식별 능력을 저하시키는 등 다양한 방식으로 영상 품질에 부정적인 영향을 미치는 것으로 나타났다[1],[2]. 이러한 문제를 해결하기 위해 다양한 재밍 회피 및 억제 기법에 대한 연구가 진행되고 있다[3]. 특히 최근 연구에서 주목 받고 있는 바이스태틱 SAR는 송신기와 수신기를 분리하여 독립적으로 운용함으로써 수신기의 위치를 노출시키지 않고 재밍 신호의 영향이 적은 곳에서 운용할 수 있는 장점이 있어 모노스태틱 SAR보다 재밍 신호 영향에 대한 저항력이 우수하다[4]. 바이스태틱 모드에서는 송/수신기가 상호 독립적으로 운용되며 일반적인 지상 재머는 레이다 송신기를 지향하여 운용되기 때문에 재밍 신호가 수신기에 미치는 영향이 상대적으로 억제된다. 또한, 위성 시스템과 달리 항공기 플랫폼은 불규칙한 운용 궤도로 인해 지상에서 송신된 재밍 신호가 수신기에 도달하는 과정에 안테나 빔 패턴과 경로 변화에 따라 불규칙한 손실이 발생할 수 있다. 이와 같이 재밍 회피에 강점을 갖는 바이스태틱 SAR에 관한 관심이 증가하고 있으며, 이를 활용한 ECCM(electronic counter counter measure) 기술의 필요성이 대두되고 있다[5],[6].
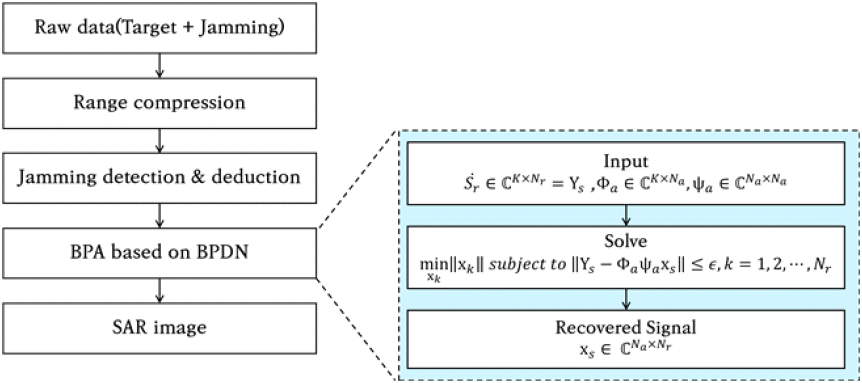
압축센싱(CS, compressive sensing)은 sub-nyquist rate로 샘플링된 데이터에서도 신호와 영상을 획득할 수 있는 접근 방식으로, 손실된 신호의 복원에 효과적으로 적용할 수 있다[7]. 본 논문에서는 바이스태틱 SAR 모드에서 수신된 신호의 일부 구간이 부분적으로 재밍 신호의 영향을 받는 시나리오를 가정하고, 이를 통해 영상의 품질 저하가 발생하는 수준을 모사한다. 더 나아가, 발생한 신호 손실을 극복하고 영상 품질을 복원하기 위한 기법을 제안한다. 이를 위해 본 논문의 Ⅱ장에서는 바이스태틱 SAR 영상 획득 과정과 재밍 신호 간섭에 따른 손실 시나리오를 정의하고 정합에 사용한 기법 및 신호 복원을 위한 압축센싱 알고리즘을 설명한다. 이어서 Ⅲ장에서는 모의실험에 사용된 주요 파라미터와 모의실험 결과를 제시한다.
Ⅱ. 이 론
바이스태틱 SAR는 모노스태틱 SAR와 달리 송/수신기가 독립적으로 운용되기 때문에 재밍 신호가 수신기에 도달하는 경로가 다양하게 변할 수 있어 수신 과정에서 재밍 신호의 손실이 발생할 가능성이 높다[8]. 특히 지상 재머는 바이스태틱 SAR 수신기의 정확한 위치를 파악하기 어렵기 때문에[9] 바이스태틱 SAR 수신기에서 전체 수신 펄스에 재밍이 일괄적으로 발생하는 것이 아닌 일부 랜덤한 펄스에만 재밍 신호가 인가될 수 있다.
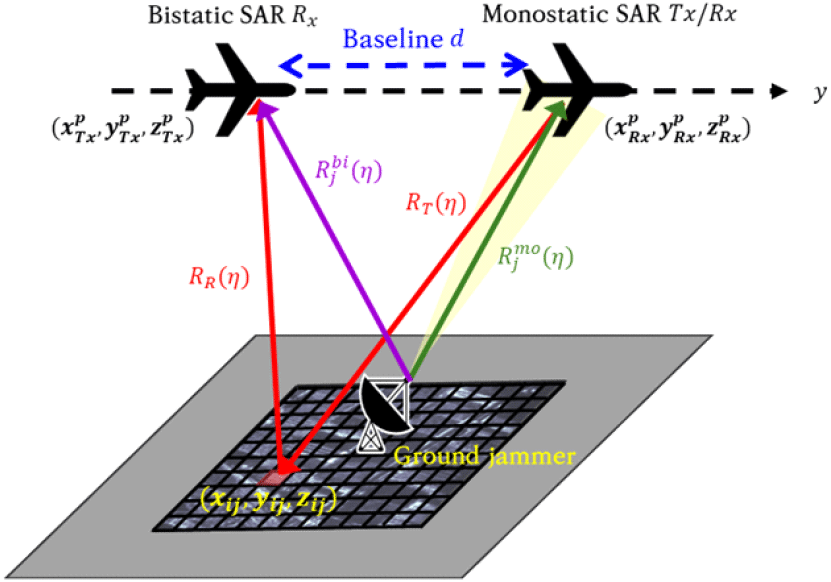
그림 1은 2기의 항공기 플랫폼을 운용하여 모노/바이스태틱 SAR 영상을 획득하는 구조를 보인다. 선행하는 항공기는 모노스태틱 모드로 송/수신기를 모두 운용하고, 후행하는 항공기는 바이스태틱 모드로 신호를 수신하는 수신기만을 탑재하고 있다. 두 항공기는 동일한 비행 경로를 공유하며, 방위 방향 성분인 y축을 기준으로 일정한 거리 d만큼 이격되어 이동한다고 가정한다. 지상 재머는 관측 영역 내에 위치하며, 모노스태틱 플랫폼에서 송신된 신호를 추적하여 재밍 신호를 방사하는 시나리오를 가정한다. 방위 방향으로 측정되는 시간을 η라고 할 때 송신기로부터 표적까지의 거리는 RT(η), 수신기로부터 표적까지의 거리는 RR(η)로 표현하며 지상 재머로부터 모노스태틱 수신기까지의 거리를 , 바이스태틱 수신기까지의 거리를 로 표현하였다. SAR 영상 내 i,j번째 픽셀의 목표물 위치는 (xij,yij,zij) 로 표현된다.
일반적인 SAR 시스템이 변조율 kr을 갖는 선형 변조 신호를 사용할 때, 수신 신호는 식 (1)과 같이 표현될 수 있다[10].
여기서 t는 fast time, η는 slow time을 나타내며, c는 빛의 속도, λ는 레이다 신호의 파장이다. σ(x, y)는 해당 좌표에 있는 표적의 반사도를 의미한다.
모노스태틱 SAR과는 달리 바이스태틱 구조에서는 송신기와 수신기가 분리되어 있어 표적과 각 플랫폼 간의 거리가 더 복잡하게 계산된다. 또한 모노스태틱과 바이스태틱 모드에서의 표적 반사도도 각각 다른 값을 갖는다. 신호처리 관점에서 보면 바이스태틱 구조에서는 송신기와 수신기의 안테나 빔 패턴이 불일치하고 두 시스템 간의 안테나 및 시간 동기화 오차가 발생할 수 있다. 이러한 특성 때문에 펄스 단위로 신호의 이동 경로를 변수로 입력하는 BPA(back-projection algorithm) 신호처리 기법을 적용하는 것이 효과적이다.
바이스태틱 SAR에서 송신기에서 전송된 신호가 표적을 거쳐 수신기까지 전달되는 경로 Rbi(η)는 그림 1에서 표현한 바와 같이 Rbi(η = RR(η + RT(η로 표현될 수 있다. 바이스태틱 구조에서 수신되는 신호는 식 (1)에서의 2R(η를 Rbi(η 대체하여 표현된다.
그림 1에서 p번째 펄스가 송수신될 때 송신기와 수신기의 위치는 각각 , 로 표기된다. 본 논문에서는 복잡도를 낮추기 위해 두 플랫폼의 x,z축 좌표는 동일하며 y축 방향으로만 d만큼의 이격 거리를 갖는다고 설정하여 ypTx = ypRx + d로 가정된다. 관측되는 영상 격자에서 (i,j)에 대응되는 픽셀의 위치 (xij, yij, zij)에서 바이스태틱 신호의 이동 경로 거리는 식 (2)와 같다.
송신기와 수신기 간 동기화가 완벽하게 이루어져 신호 손실이 발생하지 않았다고 가정할 때, dechirp 연산을 거친 바이스태틱 SAR 신호는 식 (3)과 같이 표현된다[11],[12].
식 (3)에서 A는 신호의 크기, fo는 신호의 중심 주파수를 의미한다. 바이스태틱 기하 구조를 고려하여 송신기 위치로부터 관측 영역 중심까지의 거리를 Rct(η), 수신기 위치로부터 관측 영역 중심까지의 거리를 RcR(η)라 할 때, Rc(η)는 RcR(η)와 Rct(η)의 합으로 표현되고 이때 거리 이격 ΔR(η)는 ΔR(η) = Rbi(η) − Rc(η)와 같이 구해진다.
식 (3)의 마지막 항은 ΔR(η)의 함수로 dechirp 연산 과정에서 발생하는 RVP(residual video phase) 성분을 의미한다. 모노스태틱 관측 모드에서는 RVP의 영향이 미미하지만, 플랫폼 이동 및 관측 범위의 복잡도가 증가하는 바이스태틱 시나리오에서는 영상 품질 개선을 위해 RVP 성분을 보상하여 제거하는 것이 필요하다[13].
BPA 연산은 임의의 지점과 연관된 모든 거리 압축 신호를 역투영하여 합산하는 방식으로 구현된다. SAR 영상 내의 D 지점에 위치한 픽셀의 반사도 I는 방위 방향으로 분포하는 모든 지점에서 계산된 수신 신호 S(Rη,p)의 합으로 산출된다. 이를 식으로 표현하면 식 (4)과 같다.
계산 과정에서 SAR 영상의 픽셀 간격이 실제 표적과 레이다 간의 거리와 일치하지 않아 오차가 발생할 수 있으며 이를 보정하기 위한 위상 보정항 e−jψ(η,D)가 추가되어야 한다. 이러한 위상 오차는 BPA 영상 생성 과정의 품질에 큰 영향을 미치며, 특히 송/수신기가 분리되어 독립적으로 운용되는 바이스태틱 SAR 모드에서는 매우 중요한 품질 요소로 작용한다. 바이스태틱 구조에서는 영상의 좌표 체계가 실제 레이다와 표적 간의 거리 변화를 정확하게 반영하지 못하는 경우가 발생할 수 있으며, 정확한 영상 정합을 위해서는 이를 보상하는 거리-위상 보정이 필수적으로 요구된다.
바이스태틱 SAR는 모노스태틱 SAR와 달리 송/수신기가 서로 다른 위치에 배치되어 있으므로 표적과의 상호 기하적 특성을 반영한 알고리즘을 적용해야 한다[14]. 이와 같은 구조에서는 서로 다른 플랫폼 간의 신호 전송 과정에서 자유도가 증가하게 되며, 항공기 플랫폼의 경우 이동 경로의 복잡성으로 인해 모노스태틱 SAR처럼 단순한 일반해를 구하기 어렵다. BPA 방식은 SAR 플랫폼의 불규칙한 운용 기하 구조에 대응하기 용이하여 군집으로 운용되는 SAR 관측 체계에서 활용도가 높다[15]. 고품질의 BPA 정합 영상을 획득하기 위해서는 앞 절에서 제시한 바와 같이 거리 이격에 대한 위상 오차 보정의 정밀도를 확보하는 것이 중요하다.
BPA를 통한 SAR 영상 정합 과정에서 실제 데이터가 샘플링된 위치와 생성하려는 SAR 영상의 픽셀 좌표계 간의 불일치가 발생할 수 있다. 이러한 불일치를 최소화하기 위해 측정된 데이터를 영상의 픽셀 좌표계에 맞게 보간하는 과정이 필요하다[16]. 이를 위해서는 영상 내 각 픽셀에서 목표물의 위치를 정확하게 파악해야 하며 생성된 각 픽셀의 위치는 식 (2)에서 산출된 거리값에 가장 근접하게 정합되어야 한다. 이 과정에서 발생할 수 있는 정합 오차를 최소화하는 보간 연산이 필수적이다. 이를 위해 관측 영역의 좌표가 실제 관측된 신호에서 순차적으로 샘플링되는 두 지점 사이에 존재한다고 가정한다. 관측되는 수신 신호 샘플에서 계산된 거리값을 순차적으로 Dw (w = 1,2, &)라 표기하면, 보간 영역은 식 (2)로 주어지는 실제 신호 이동 경로와의 차이가 최소가 되는 w는 식 (5)를 만족한다.
거리 해상도는 ΔD=Dw−Dw−1로 주어지며, 수신단에서의 샘플링 속도가 FS로 주어질 때, ΔD=c/2Fs로 정의된다. 격자를 구하기 위한 식 (4)에 적용될 BPA 적용 신호는 식 (5)에서 지정된 2개의 수신 신호로부터 보간하여 얻을 수 있다. 가중치를 적용하는 보간 방식으로 구현하는 수식은 식 (6)과 같이 표현될 수 있다.
여기서 S[Dl]은 격자 지점으로부터 반사된 신호에서 Dl 거리 구간에 해당하는 값이고 은 이를 보간한 신호값이다. 이와 같이 모든 펄스에 대해 보간 연산을 수행한 후, 잔여 위상에 의해 발생하는 위상 오차를 보정하여 SAR 영상을 생성한다. 최종 정합된 영상 ISAR(i,j)는 식 (7)과 같이 표현된다.
Npulse는 BPA 영상 정합 과정에서 단일 점 표적을 생성하는 데 필요한 펄스 수이다. 이는 송/수신기의 안테나 패턴 및 이격 거리 등에 의해 결정된다.
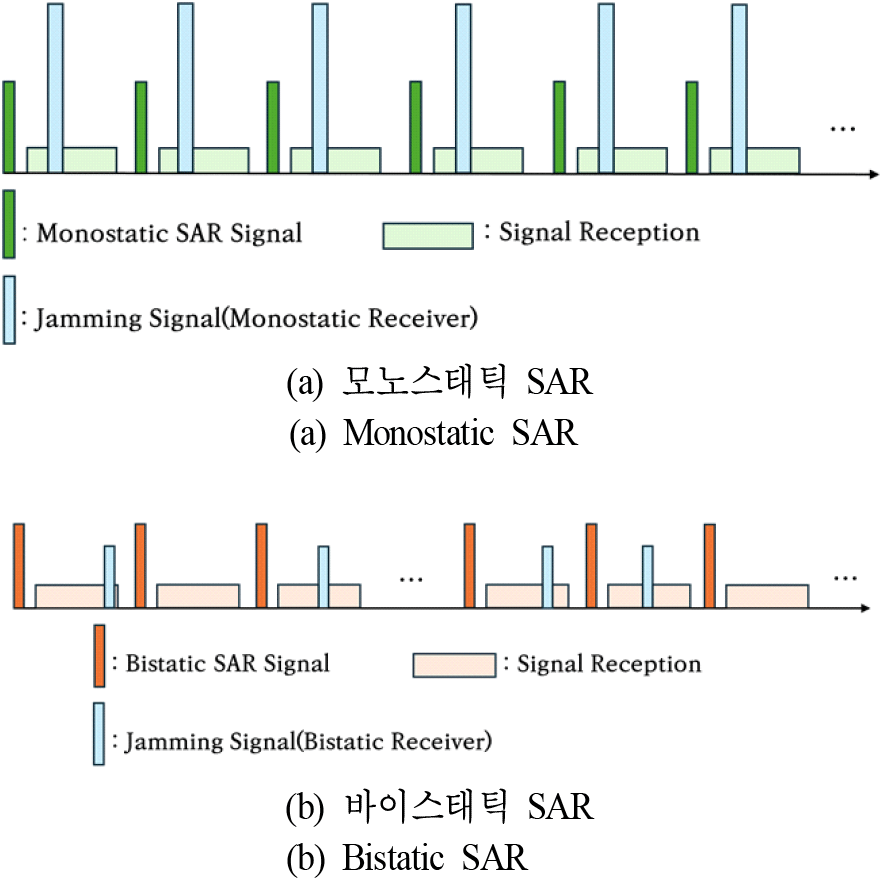
일반적으로 지상 재머는 주로 모노스태틱 SAR의 송신 신호에 대응하여 재밍을 수행하므로 바이스태틱 SAR 수신기에 미치는 영향은 상대적으로 매우 낮다. 바이스태틱 SAR는 재밍 신호의 유입을 회피하기 위해 운용되지만 실제로는 안테나의 부엽 신호, 플랫폼 궤적의 요동, 재머 안테나의 지향 오차 등 다양한 요인으로 인해 불규칙한 방식으로 재밍 신호가 유입될 수 있다. 따라서 모노스태틱 SAR 수신기에는 일정한 간격으로 재밍 신호가 침투하는 반면, 바이스태틱 SAR 수신기에는 시간 축에서 랜덤한 방식으로 재밍 신호 패턴이 나타날 수 있다. 바이스태틱 수신 신호와 함께 유입되는 재밍 신호의 강도가 충분히 클 경우, 해당 구간의 표적 신호는 손실된 것으로 간주된다. 그림 2는 이러한 가정에 따라 모노스태틱 SAR와 바이스태틱 SAR 수신기에서의 송/수신 신호 및 재밍 신호가 시간 영역에서 나타나는 과정을 도시한다. 일정한 패턴을 갖는 모노스태틱 수신기와는 달리 바이스태틱 수신기에서의 재밍은 신호가 영향을 주는 구간이 불규칙적이며 신호의 강도가 상대적으로 약하게 표현된다.
레이다 송신 신호 S는 표적에서 반사된 후 재밍 신호 와 혼합되어 레이다 수신부에 유입된다. 신호 S는 표적의 반사계수 σ와 이동 경로에 따른 감쇄의 영향을 받으며 모노스태틱 및 바이스태틱 수신부에서 각각 와 의 시간 지연이 발생한다. 재밍 신호 역시 각각 , 에 따라 서로 다른 지연을 갖는다. 여기서 잡음 n(t)를 고려한 수신 신호 는 식 (8)과 같이 표현된다.
식 (8)에서 는 Na × Nr 크기의 지상 영역에서 반사된 신호를 나타낸다. 지상에는 NJ개의 재머가 존재하며 Ji는 i번째 재머로부터 수신되는 재밍 신호이다.
본 논문에서는 DRFM(digital radio frequency memory) 기반의 잡음 변조 신호를 사용하는 재밍 시스템을 가정하였으며 송출되는 재밍 신호는 식 (9)와 같이 정의된다[17].
여기서 는 레일리 분포를 따르는 신호 강도, fj는 재밍 신호의 주파수, φ(t)는 [0,2π] 영역에 균일하게 분포하는 난수이다. fj는 SAR 시스템의 중심 주파수와 동일하며 재밍 신호의 크기는 위성과 재머의 위치에 따라 변하는 JSR(jamming to signal ratio) 요구값을 충족한다고 가정한다. 플랫폼 이동 경로에 따른 거리 변화값을 구하기 위해 STK(system tool kit)를 사용하여 항공기 플랫폼의 이동에 따른 재머와의 거리 변화를 추정하였으며 이를 기반으로 JSR 값을 산출하고 이에 대응하는 재밍 신호의 크기를 결정하였다.
방위 시간 η와 거리 시간 t를 반영한 수신 신호를 포함하여 식 (8)을 행렬식으로 표현하면 식 (10)과 같이 나타낼 수 있다.
식 (10)에서 s(ηp,tq)는 방위 시간 ηp, 거리 시간 tq에서의 수신 신호를 의미한다. 영역에서의 는 재밍 신호 행렬로서 그림 2와 같이 모노스태틱과 바이스태틱 수신기에 서로 다른 방식으로 유입되며 이에 대한 변환식을 각각 Tmo과 Tbi라고 하면 식 (11)과 같이 표현될 수 있다.
여기서 은 dn번째 재밍 신호의 시간 지연으로 모노스태틱의 경우 각 행에서의 시간 지연값은 일정한 상수가 되어 로 가정할 수 있다. 반면 바이스태틱 모드에서는 각 행에서의 시간 지연값은 그림 2와 같이 불규칙한 방식으로 산출된다. 또한 모노스태틱 SAR에서는 모든 신호 구간에서 재밍 신호가 유입되므로 Tmo은 단위 행렬식과 같으나 바이스태틱 SAR에서는 각 재밍 신호의 시간 지연이 불규칙하게 표현되며 변환식 Tbi는 식 (12)와 같은 랜덤 행렬식으로 표현된다.
표적 신호에 대해 거리방향 압축을 수행한 신호(RGC data)를 이라고 할 때, 은 식 (13)와 같이 표현된다[11].
재밍 환경에서 유입된 신호를 제거할 경우, 재밍이 발생한 모든 영역은 손실 구간으로 간주된다. 이때 방위 방향으로 정렬된 신호에서 식 (12)의 변환식에서 표현되는 신호 분포 영역을 제거하면 그림 3과 같은 분포를 갖는 로 변형된다.
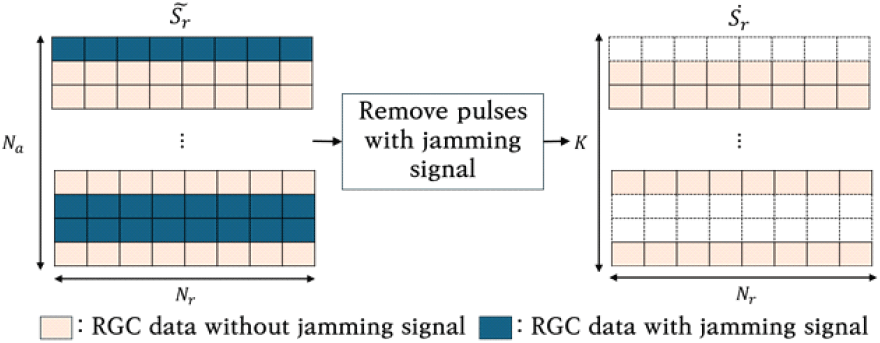
잡음 변조 기반의 재밍 신호가 포함된 수신 펄스를 처리하는 과정에서 신호의 강도 및 주파수 특성, 처리 영상에서의 잡음 증가 등 이상 징후가 발견된 경우 이를 식별하여 해당 수신 신호를 제거하는 시나리오를 가정하였다. 따라서 유효 수신 펄스 수 는 감소되며 재밍 신호에 의해 오염된 펄스의 수를Njammed라 할 때 K=Na−Njammed로 계산된다.
그림 3과 같이 재밍 신호를 포함하는 펄스를 강제적으로 제거하면 영상 내에서 재밍 신호의 영향을 제거할 수는 있지만, 최종적으로 획득된 정합 영상에서 손실된 구간으로 인해 품질 저하가 발생하게 된다. 본 논문에서는 이를 극복하기 위해 인위적으로 발생한 손실 구간을 복원하는 압축센싱 기반 알고리즘을 도입한다.
압축센싱은 선형 방정식으로 구성된 시스템에서 주어진 관측 데이터보다 큰 크기의 원본 데이터를 복구하는 방법을 제시한다. 이러한 시스템은 식 (14)와 같이 표현할 수 있다.
y는 관측한 신호, A는 관측 행렬, N은 잡음 신호 행렬, x는 복원하고자 하는 원신호를 의미한다. 압축센싱의 핵심 요소는 산재성(sparsity)과 랜덤 샘플링이다. 압축센싱에서는 적은 수의 샘플을 통해 신호를 복원하기 위해 신호의 산재성을 활용한다. 즉, 랜덤하게 추출된 샘플들을 통해 적은 간격의 측정 샘플로 높은 주파수 성분을, 큰 간격의 샘플로 낮은 주파수 성분을 추정하게 된다. 이를 통해 필요한 측정 샘플 수를 줄이고 원신호의 산재된 성분을 추정하여 복원할 수 있다. 압축센싱에서 복원하고자 하는 신호 x는 특정 산재성과 RIP(restricted isometry property) 조건을 만족해야 한다[18],[19]. 본 논문에서는 일부의 신호만을 사용하더라도 산재 분포된 표적 정보를 복원할 수 있음을 활용하여 재밍에 의해 손실된 SAR 데이터를 처리하여 해당 영역의 표적 영상을 생성한다.
그림 3에서 재밍 신호의 영향을 받은 펄스를 제거하여 손실이 발생한 신호 를 라고 할 때, 복원하고자 하는 희소 신호와 측정된 신호 간의 관계식을 결정하는 선형 방정식은 식 (15)와 같이 표현할 수 있다.
는 원래 신호에서 무작위로 샘플링을 수행하는 행렬로 본 논문에 적용된 재밍 시나리오에서 랜덤 샘플링 행렬은 가우시안 랜덤 샘플 행렬 Φrand과 식 (11)에서 정의된 랜덤 재밍 신호 분포 행렬 Tmo,bi의 곱인 Φa=ΦrandTmo,bi로 표현된다. 는 표적 영역을 수집하는 수신 신호의 생성 행렬이며 본 논문에서는 BPA 연산 행렬에 의해 표적 영역을 복원하는 과정의 역행렬로 표현된다. BPA 연산행렬 를 로 표현할 때[20], 은 보간 연산 행렬로 측정된 신호를 영상의 픽셀 좌표계에 맞게 보간을 수행하며 여기서 Np는 픽셀 좌표계 내의 전체 픽셀 수를 의미한다. 는 식 (6)에서 기술한 보간된 신호에 대해 위상 오차를 보정하고 합산 연산을 수행하는 행렬이다. 바이스태틱 SAR 신호의 위상 오차 보정식은 식 (7)의 마지막 항과 같이 정의된다. 는 표적 응답 행렬로서 최종 SAR 영상을 의미한다. 본 논문에서는 재밍과 같은 잡음 성분이 포함된 희소 신호의 복원에 유리한 l1-최소화 기법 기반의 BPDN(basis pursuit de-noising) 알고리즘을 적용한다. 잡음 성분을 고려한 l1-최소화 문제는 식 (16)과 같이 정의된다.
여기서 ε은 신호 복원의 임계값이다. 압축센싱 알고리즘을 거리와 방위 방향으로 동시에 적용할 경우 신호 검출 행렬의 크기가 (Na×Nr)×(Na×Nr)로 증가하므로 메모리 사용 및 연산속도 문제에 직면하게 된다. 따라서 본 논문에서는 방위 방향의 BPA 알고리즘 적용 과정에서만 압축센싱을 적용한다. 특히 방위 방향으로의 신호 손실을 가정하였으므로 주어진 문제에 적절한 시나리오라고 할 수 있다.
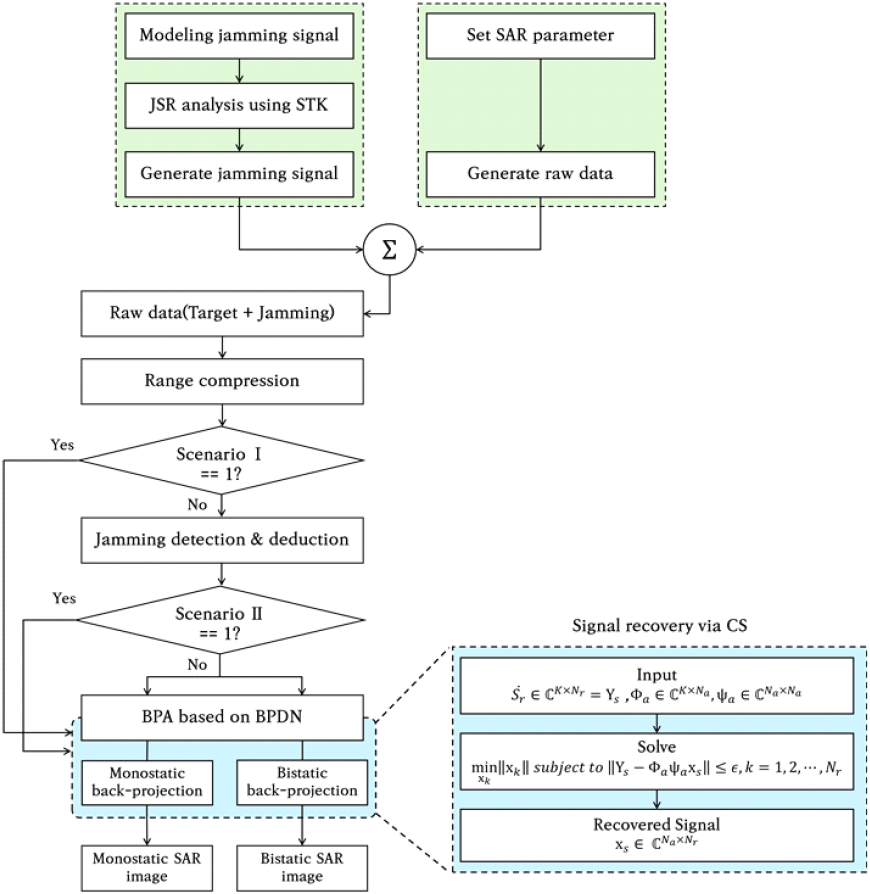
본 논문에서는 식 (16)의 조건을 만족하는 최적화된 표적 응답 행렬을 복원하는 방식으로 재밍 신호의 영향을 최소화하는 알고리즘을 구현하였다. 이 알고리즘은 재밍 신호를 강제적으로 제거함으로써 발생한 신호 손실을 압축센싱을 활용하여 복원하여 신호 손실에 따른 SAR 영상 품질 저하를 방지한다. 본 논문에서 제안한 알고리즘의 블록도는 그림 4에서 보인다.
본 논문에서 사용한 알고리즘은 재밍의 영향을 제거하기 위해 재밍 신호에 영향을 받은 신호 구간을 강제로 제거한다. 재밍 신호의 경우 불규칙한 패턴으로 수신 신호에 인가되기 때문에 랜덤 샘플링을 적용하여 재밍 신호의 영향을 받지 않은 수신 신호를 선별적으로 획득할 수 있다. 그러나 획득한 신호는 재밍 신호 제거로 인해 샘플이 부족하여 신호처리 후 영상의 품질이 저하될 가능성이 있다. 이를 해결하기 위해 본 논문에서는 방위 방향 신호처리 과정에서 압축센싱 기법을 적용하여 부족한 샘플 문제를 보완하고 재밍 신호의 영향이 제거된 고품질 SAR 영상을 획득하는 알고리즘을 제안한다.
Ⅲ. 재밍 모의실험 수행
그림 1의 환경을 모사하여 재밍 모의실험 환경을 구축하였다. 모의실험을 위한 SAR 플랫폼은 실제 운용 사례를 참고하였으며 각 세부 제원은 표 1 및 표 2에서 보인다[21].
| SAR system parameters | Value |
| fo | 5.3 GHz |
| Bandwidth | 300 MHz |
| Beam width | 1.1° |
| Pulse width | 2.5 μS |
| PRF | 0.5 kHz |
| Antenna gain Tx/Rx (monostatic/bistatic) | 30 dBi |
| Transmitted power | 40 dBw |
| SAR platform parameters | Value |
| Altitude | 5 km |
| Closest distance from platform trajectory to scene center | 10 km |
| Platform velocity (Tx/Rx) | 200 m/s |
| Baseline | 1.5 km |
지상 재머는 관측 영역 내에 위치하며 모노스태틱 SAR 항공기 플랫폼을 지향하며 운용된다고 가정한다. 재머는 DRFM 방식으로 운용되며 출력과 안테나 이득은 모노스태틱 SAR 수신단의 SNR(signal to noise ratio)을 초과하여 충분히 큰 JSR을 갖도록 설정하였다.
재밍 신호가 인가되었을 때, 모노스태틱과 바이스태틱 SAR 영상 내에 나타나는 영향과 재밍 신호 제거로 인한 신호 손실을 압축센싱 기법을 통해 복원할 수 있는지를 확인하기 위해 다음 세 가지 시나리오에 대해 모의실험을 수행하였다.
-
- Scenario I: 재밍 신호 유입에 따른 영상 품질 저하
-
- Scenario II: 수신단에서 재밍 신호 제거 후 발생한 신호 손실
-
- Scenario III: 신호 손실 신호 복원을 위한 압축센싱 기법 적용
모노스태틱 SAR의 경우 모든 수신 신호가 100 % 재밍 간섭을 받는 반면 바이스태틱 SAR 수신단에서는 그림 2에 도시한 바와 같이 일부 구간에만 간섭 신호가 유입된다. 신호 손실 정도에 따른 영향을 분석하기 위해 전체 수신 펄스 중 일부 구간이 재밍 영향을 받아 손실되는 것을 가정하여 모의실험을 수행하였다.
모의실험을 통해 생성된 영상을 정량적으로 평가하기 위해 사용한 지표는 다음과 같다. 먼저, 재밍 신호의 영향을 받은 영상을 평가하기 위한 유클리드 거리(Euclidean distance) d(x,y)는 식 (17)과 같이 계산된다[17].
식 (17)에서 x=(α1,…αl)와 y=(β1,…βl)는 각각 재밍 이 발생하기 전과 후에 측정된 SAR 영상의 화소값이다. 다음으로 SSIM(structural similarity index measure)은 영상의 구조적 유사도를 평가하기 위해 사용되는 지표로, 재밍에 의한 신호 손실 및 복원 효과를 산출하는 지표로 활용된다.
구현된 복원 알고리즘의 성능을 평가하기 위해 SAR 수신단에서 발생한 신호 손실의 영향과 복원 성능을 측정하기 위한 점 표적 모의실험을 수행하였다. 이 실험에서는 수신 신호 중 일부가 손실되는 시나리오를 가정하여 방위 방향으로 인위적인 손실을 부여한 후 품질 저하를 측정한다. 그 다음 식 (16)에서 제시한 압축센싱 기법을 적용하여 복원된 영상 품질을 비교하였다. 모의실험을 통해 획득한 점 표적의 1차원 방위 방향 응답은 그림 5에 나타나있다. Case A는 신호 손실이 없는 시나리오에서 획득된 결과, Case B는 30 %의 신호 손실이 발생한 경우, Case C는 30 %의 신호 손실 후 압축센싱 기반 신호 복원 알고리즘을 적용한 결과이다. 신호 손실률을 50 %로 증가시킨 실험 결과는 각각 Case B'(50 % 손실), C'(50 % 손실 후 복원)로 표기하였다. 바이스태틱 SAR에서는 모노스태틱 SAR에 비해 도플러 대역폭이 줄어들어 방위 방향 해상도가 저하되며, 이는 플랫폼 간의 이격 거리에 의해 결정된다[22].
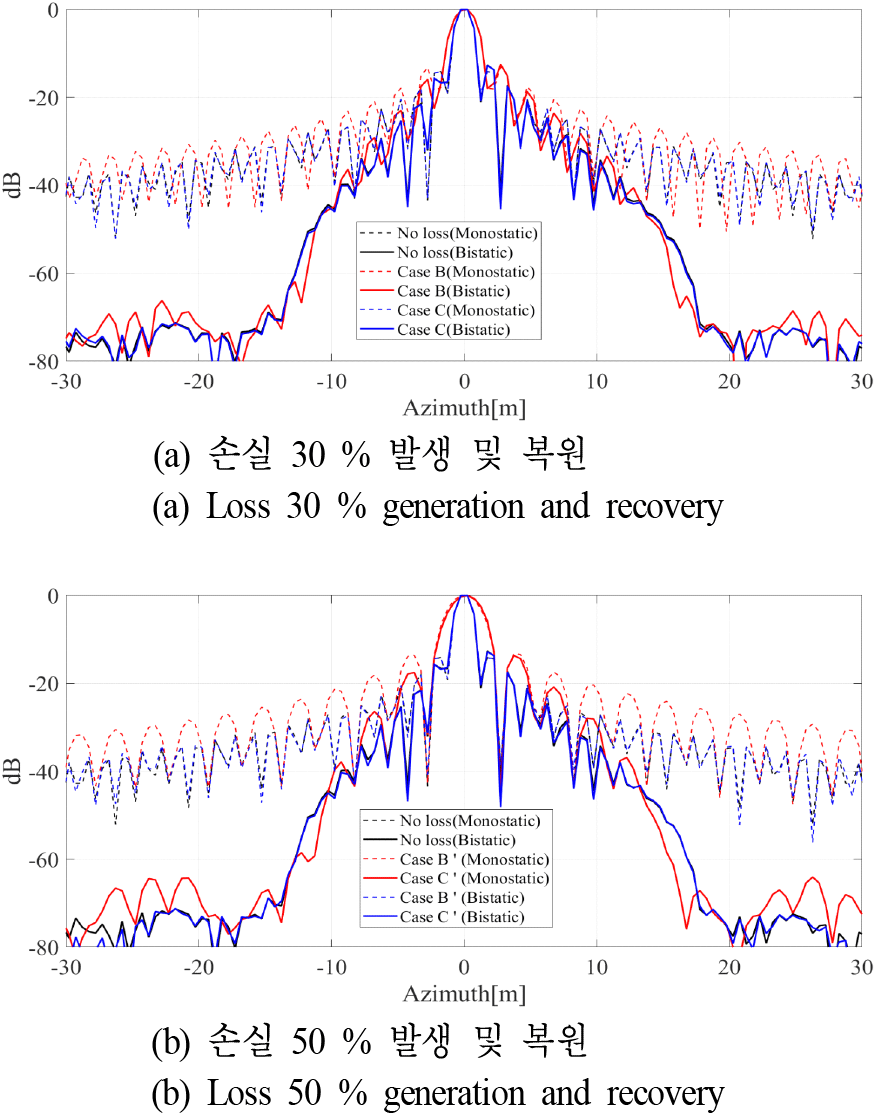
본 논문에서 가정한 시나리오에서는 모노/바이스태틱 SAR 모드에서 각각의 방위 해상도가 1.2/1.6 m로 얻어진다. 수신 신호에서 손실이 발생하면 해상도 품질이 저하되는데, 손실률이 30 %일 때 모노/바이스태틱 SAR 모드 해상도는 각각 1.9/2 m로 저하되고, 손실률이 50 %로 증가하면 2.8/3 m로 저하된다. 그러나 이러한 손실 데이터에 압축센싱 기반 복원 시나리오를 적용하면 방위 방향 응답 특성은 손실이 발생하지 않았을 때와 동일한 수준으로 복구됨을 확인할 수 있다. 각 시나리오에 대해 방위 방향 IRW(impulse response width)를 측정한 결과는 표 3에 제시하였다. 전체 신호 중 70 %의 손실이 발생하는 경우에도 모노/바이스태틱 모두 원래의 해상도 품질을 복구할 수 있다. 손실률 70 %로 증가시킨 실험 결과는 각각 Case D(70 % 손실), D’(70 % 손실 후 복원)로 표기하였다. 70 %로 손실이 증가하면 모노/바이스태틱 모두 해상도 저하가 심해지지만, 손실 복원을 통해 완전 복원이 가능함을 알 수 있다. 이를 재밍 시나리오에 적용하여 간섭의 영향을 받은 수신 펄스 구간의 신호를 강제로 제거한 후, 잔여 신호를 기반으로 신호 복원을 수행하는 알고리즘을 구현할 수 있을 것이다. 이러한 알고리즘은 재밍 신호로 인해 손실된 데이터를 효과적으로 복원하여 영상 품질 저하를 최소화할 수 있다.
단일 점표적에 대한 모의 실험의 경우 표적 산재도가 높아 복구 성능이 매우 우수하다. 표적이 클러터가 분포하는 영역일 경우 복구 성능이 낮아질 가능성이 있다. 이를 모사하기 위해서는 실제 SAR 영상을 표적으로 한 실험이 필요하게 된다.
STK는 위성, 항공기 등 다양한 플랫폼에서 운용되는 레이다 및 통신 시스템의 시뮬레이션을 지원하며 SAR 모듈, 재머 시스템 사양 및 안테나 빔 패턴을 임의로 설정할 수 있는 환경을 제공한다[23]. 본 논문에서는 모노스태틱 및 바이스태틱 SAR 항공기 플랫폼의 재밍 환경을 모사하여 각 수신단에 인가되는 JSR을 모든 관측 구간에 대해 도출한 후 이를 SAR 모의실험의 입력 데이터로 반영하였다. 재밍 모의실험 수행 과정은 그림 6에 제시되어 있다. 그림 6(a)는 그림 1에서 제시된 시나리오를 구현한 것으로 모노스태틱 SAR 모드로 운용되는 항공기와 일정한 간격으로 수신 모드의 바이스태틱 레이다 항공기 플랫폼이 함께 이동하는 상황을 모사한다. 그림 6(b)는 관측 영역에 위치한 지상 재머가 송신 신호를 방사하여 모노스태틱 SAR 플랫폼의 송신기를 추적하는 시나리오를 나타낸다. 여기서 바이스태틱 SAR 수신단은 일부 구간에서만 무작위로 재밍 신호의 영향을 받는다.
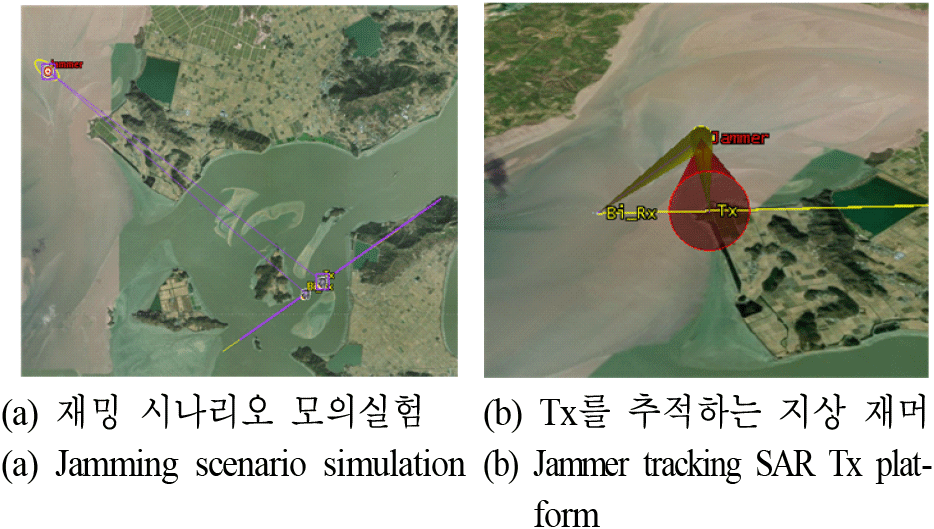
높은 이득의 안테나를 장착한 고출력 지상 재머를 가정하였을 때 측정된 평균 JSR은 바이스태틱 SAR 수신기에서 8.95 dB, 모노스태틱 SAR 수신기에서 26.8 dB로 산출되었다. 바이스태틱 SAR에 유입되는 재밍 신호는 주로 안테나 지향 오차 및 항공기 궤적 변화로 인해 무작위로 발생하는 것으로 설정하였다.
모의실험의 입력 데이터로 실제 획득된 SAR 표적 영상을 사용하였다. 그림 7은 본 논문에서 구현한 재밍 SAR 모의실험 및 압축센싱을 통한 신호 복원 시나리오를 단계별로 나타낸 것이다. 그림 8은 재밍이 발생한 후 모노스태틱 SAR의 영상 변화를 모사한 결과를 보인다. 추적 레이다를 사용하는 지상 재머에 의해 모노스태틱 SAR 수신기에 100 % 고출력 재밍 신호가 유입될 경우, 잡음 신호로 의해 영상 내부의 정보가 완전히 손실되는 것을 확인할 수 있다. 그림 9는 모노스태틱 SAR 수신기에 강제적으로 재밍 신호에 각각 30 %와 50 %에 해당하는 신호를 제거한 결과를 보이고 그림 10은 손실에 대응하기 위해신호 제거 후 압축센싱 기반 신호 복원 알고리즘을 적용한 결과이다. 재밍 신호를 제거하더라도 영상의 정보가 완전히 손실되어 영상을 복원할 수 없다.

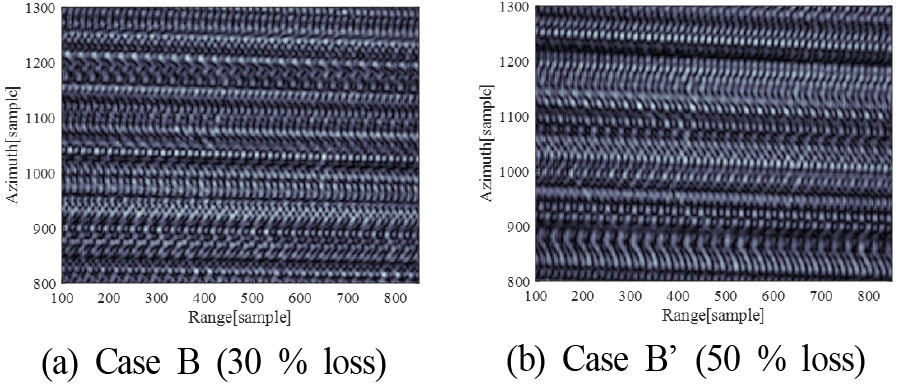
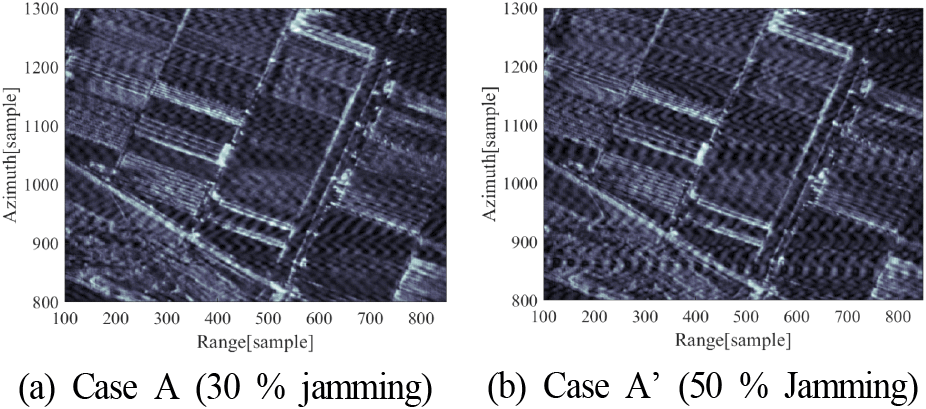
반면, 바이스태틱 SAR 모드에서는 재밍 신호가 상당 부분 회피되거나 감쇄된 후 일부만 유입된다. 그림 11은 일부 구간에서 재밍이 유입되는 Case A 시나리오에서 바이스태틱 SAR로 획득한 영상을 보인다. 재밍 신호는 안테나 부엽 방향으로 유입되므로 모노스태틱 SAR에 비해 재밍 효과는 약하지만, 전체적으로 잡음이 증가하여 영상 품질이 저하된다. 특히 30 %에 비해 50 %의 재밍 신호가 유입될 때 품질 저하가 더욱 두드러지게 나타난다.
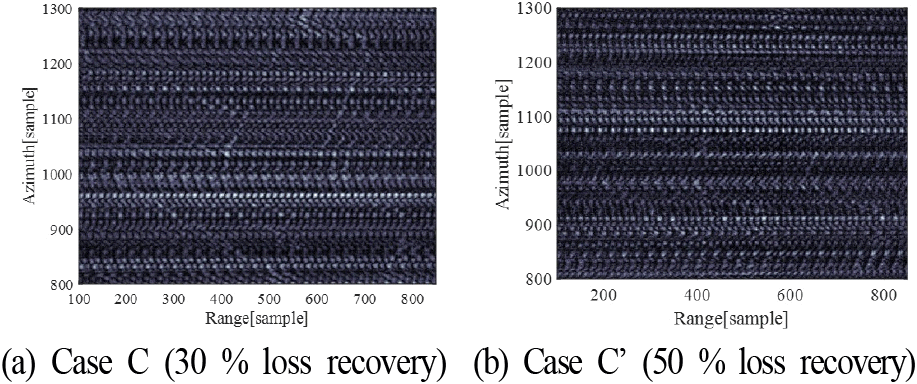
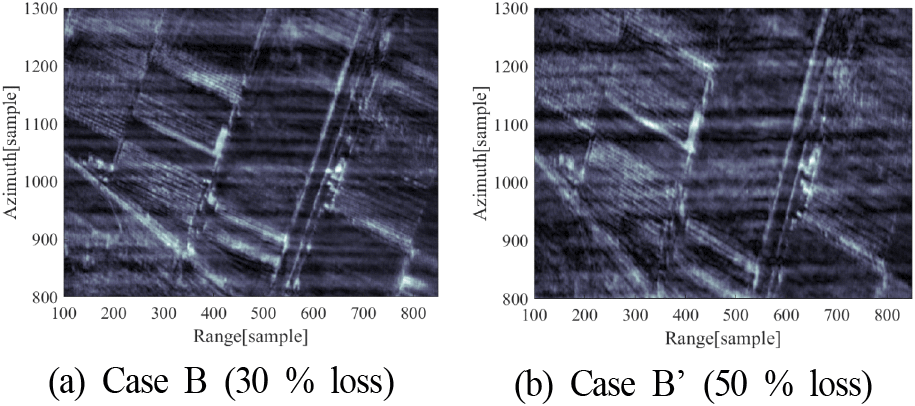
잡음 억제를 위해 재밍이 유입된 펄스 신호를 강제로 제거한 경우를 그림 12에서 보인다. 재밍 잡음은 제거되었으나, 정보가 손실되어 해상도가 크게 저하된 영상이 얻어진다. 이러한 손실에 대응하기 위해 압축센싱 기반 복원 알고리즘을 적용한 결과는 그림 13에서 보인다. 50 % 손실 데이터의 경우 완전한 복원은 어려웠으나 30 % 손실 데이터를 복원했을 때 영상 품질이 매우 우수하게 향상된 것을 확인할 수 있다. 각 Case에서 획득한 바이스태틱 SAR 영상의 품질 분석 결과는 표 4에 나타내었다.

| Mode | d(x,y) | SSIM | ||
| jamming rate | 30 % | 50 % | 30 % | 50 % |
| Case A (jamming only) | 28.02 | 35.66 | 0.74 | 0.67 |
| Case B (signal loss) | 90.96 | 92.82 | 0.29 | 0.27 |
| Case C (after recovery) | 2.87 | 22.91 | 0.99 | 0.81 |
모노스태틱 SAR 신호는 바이스태틱 SAR 신호에 비해 재밍 신호의 영향을 크게 받아 평균 JSR이 더 높게 측정되었으며, 그로 인해 최종 획득 영상의 품질이 바이스태틱 SAR 영상에 비해 낮았다. 모노스태틱 SAR 시나리오에서 모든 수신 펄스에 고출력 재밍 신호가 인가되면 높은 JSR로 의해 원신호가 완전히 손실되어 신호 복원을 통한 품질 개선이 매우 어렵다. 반면, 바이스태틱 SAR 모드에서는 상대적으로 JSR이 낮고 재밍이 발생하는 구간이 일부에 제한되어 있어 신호 복원 알고리즘을 적용할 수 있다. 재밍 신호를 강제적으로 제거하면 SAR 영상에서 재밍 신호의 영향은 사라지지만, 신호 손실로 인해 영상 품질이 크게 저하된다. 그러나 압축센싱을 통해 신호를 복원하면 재밍 신호와 신호 손실에 의한 영향을 억제하여 높은 영상 품질의 영상을 획득할 수 있다. 특히, 재밍 발생 구간이 30 % 내로 제한될 경우 매우 높은 영상 품질로 복원할 수 있다. 유클리드 거리와 SSIM 분석 결과, 30 % 손실된 신호는 원래의 영상과 유사한 품질로 복원되는 반면, 재밍 신호가 50 % 구간에 걸쳐 유입되면 품질 복원 성능이 다소 저하되는 것으로 나타났다. 따라서, 바이스태틱 모드에서도 송신기와 수신기 간의 이격 거리를 충분히 크게 설정하여 재밍 유입 구간을 줄이는 것이 필요하다.
바이스태틱 SAR 수신기와 모노스태틱 SAR 간의 이격이 줄어들 경우 재밍율은 더욱 상승할 수 있다. 재밍율을 70 %까지 증가할 때 신호 복원을 수행한 결과는 그림 14와 같다. 전체 신호의 70 %에 해당하는 재밍 신호가 유입될 경우에도 바이스태틱 SAR 영상은 품질 저하 수준은 높긴 하나 산재 표적의 형태는 잔존함을 알 수 있다.
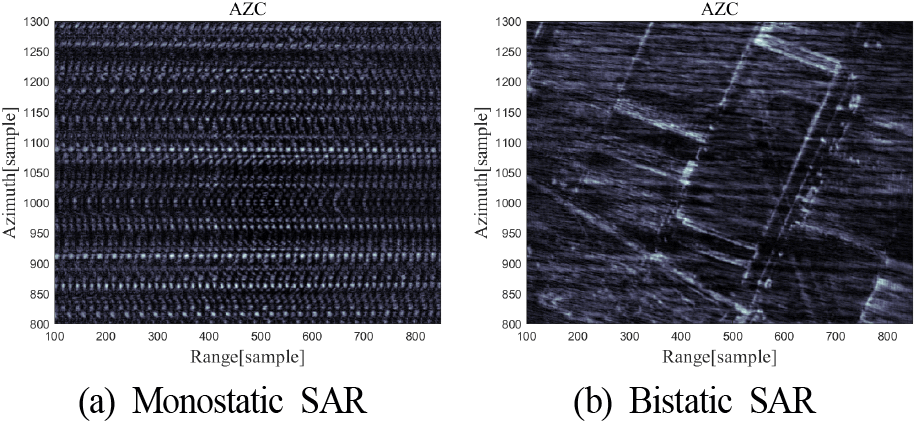
표 5는 표적이 70 % 재밍 유입에 따른 바이스태틱 SAR영상의 품질 수준을 보인다. 전반적으로 영상의 유클리드 거리와 SSIM 지표값이 급격하게 저하됨을 확인할 수 있다. 복구 과정에서 재밍 신호가 일부만 제거 복원되고 일부는 잔존하는 경우 영상 품질 개선 성능도 저하된다. Case D는 Case B 대비 50 %의 재밍 신호만 제거 후 복원된 것으로서 100 %가 복원되는 Case C에 비해 매우 낮고 Case A, 즉 재밍 영상과 동일한 수준까지 떨어지는 것을 알 수 있다. 따라서 안티 재밍 목적으로 바이스태틱 SAR를 운용할 경우 바이스태틱 SAR 수신기가 적절한 이격을 유지하여 재밍율을 낮추는 것이 필요하다.
| Mode | d(x,y) | SSIM |
| 70 % Jamming only | 44.04 | 0.35 |
| 70 % loss | 99.33 | 0.23 |
| 70 % Loss & recovery | 77.94 | 0.78 |
| 70 % Partial recovery (35 % jamming & 35 % recovery) | 40.24 | 0.71 |
Ⅳ. 결 론
본 논문에서는 재밍 환경에서 독립적으로 운용되는 송/수신기를 갖는 바이스태틱 SAR 모드에서 부분적으로 재밍 영향을 받은 시나리오를 분석하였다. 바이스태틱 SAR 신호에 재밍 신호가 유입된 경우, 해당 신호를 제거한 후 압축센싱 기법을 적용하여 신호를 복원함으로써 영상 품질 저하를 억제하는 방식을 제안하였다. 이를 통해 재밍 환경에서 운용되는 모노스태틱 SAR의 영상 품질이 저하되거나 손실되는 상황에서도, 함께 운용되는 바이스태틱 SAR 수신단에서는 재밍 신호의 영향이 억제된 고품질 영상을 확보할 수 있음을 보였다. 다만, 압축센싱 복원 성능은 복원하고자 하는 신호의 산재성에 큰 영향을 받는다. 본 논문에서 수행한 실험 결과, 50 % 이상의 신호 손실이 발생한 경우 복원 성능이 급격히 저하되는 것을 확인하였다. 실제로 70 %의 신호 손실이 발생한 실험에서는 복원 성능이 크게 저하되는 것을 확인하였으며, 이는 제안된 방법의 성능 한계를 나타낸다. 이러한 결과는 바이스태틱 SAR 운용 과정에서 발생할 수 있는 송/수신기 간 시간 동기 오차 및 안테나 지향 오차로 인한 신호 손실에도 적용 가능할 것으로 예상되며, 향후 이러한 한계를 보완하기 위한 추가 연구가 필요할 것이다.