Triaxial Method의 구조적 특성을 고려한 단일 편조 RF 케이블의 차폐 모델에 대한 연구

Ⅰ. 서 론

RF 케이블은 전기 자동차, 항공 우주, 방위 산업 분야에서 케이블 어셈블리로서 다양하게 사용되고 있다. 이는 고전압, 고출력 시스템에 사용되고 필연적으로 전자기 간섭(EMI)을 발생시켜 전자파 적합 테스트(EMC)에 민감한 결과를 초래한다. 유럽 전기 표준화 위원회(CENELEC, European Committee For Electrotechnical Standardization)에서 규정한 EN55022/032, MIL-STD-461G 그리고 기타 관련 표준의 복사 방출(radiation emission) 임계값을 초과하는 것이 주로 상호 연결된 전원 케이블과 케이블의 커넥터에 집중되어 있다고 나타났다. 따라서 케이블의 차폐 정도를 판단하는 매개변수인 전달 임피던스의 측정이 중요해지고 있다^[1]~[3].

케이블의 전달 임피던스를 측정할 수 있는 Triaxial 방법의 표준으로는 유럽 전기 표준화 위원회에서 규정한 EN 50289와 전기 기술 위원회(IEC, International Electro -technical Commission)에서 규정한 IEC 62153가 있다^[4],[5].

Triaxial 방법을 사용하기 위해서는 외부 튜브로 사용되는 구리 파이프를 사용해야하여 무겁고, 케이블의 크기와 테스트 구조를 재구성하는 것이 필요하다는 단점이 존재한다. 셋업을 재현하여 측정하더라도 Triaxial 방법의 구조적 특성을 고려하지 않았기 때문에 Demoulin의 전달 임피던스 이론 수식과 비교하는 것은 적절하지 않다.

따라서 본 논문에서는 Triaxial 방법의 구조적 특성을 고려하여 수정된 Demoulin 이론 수식을 제안하고자 한다. Ⅱ장에서는 제작한 Triaxial 구조 및 회로도를 제시하여 측정되는 S 파라미터를 이용해 유도된 전달 임피던스 수식을 기술한다. Ⅲ장에서는 Demoulin 전달 임피던스 이론 수식을 이루고 있는 각 항을 케이블의 등가 회로를 통해 설명하고, 주파수에 따른 각 항의 지배적인 구간을 설명한다. 그리고 Triaxial 방법으로 측정 시 쉴드와 외부 튜브가 맞닿아 있는 구조적 특성을 고려하여 수정된 Demoulin 이론 수식 및 등가 회로를 제안하고자 한다. Ⅳ장에서는 Ⅱ장에서 제작한 Triaxial을 통해 측정된 전달 임피던스와 Ⅲ장의 Demoulin 이론 수식, 그리고 수정된 Demoulin 이론 수식을 비교한다. 오차를 통해 Triaxial 방 법의 구조적 특성을 고려하여 수정된 이론 수식 해석 결과가 측정과의 정합성이 더 좋은 것을 확인하고자 한다.

Ⅱ. 전달 임피던스 측정 방법

2-1 단위 길이당 전달 임피던스

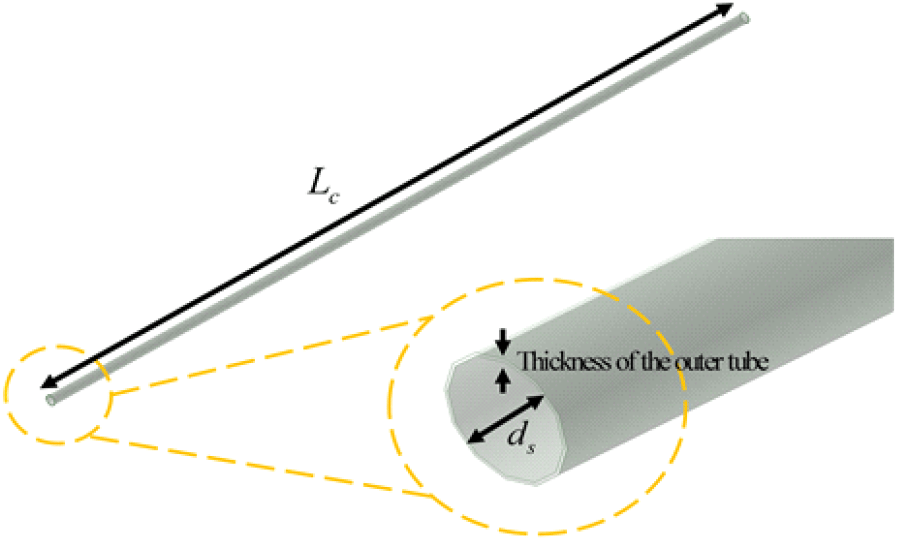
케이블의 단위 길이당 전달 임피던스는 표면 전달 임피던스로 알려져 있으며, 전기적으로 커플링 되는 짧은 길이 L_c의 케이블의 경우 공급 전류 I₁을 쉴드층에 흘려 주었을 때 케이블 쉴드 기준 외부 도체로 전압 V₂가 유도된다. 이때 유도된 전압을 단위 길이당 케이블 쉴드층에 흐르는 전류로 나눈 값을 의미한다. 수식은 식 (1)과 같고, 수식에 대한 케이블의 구조는 그림 1과 같다.

$$Z_T=\frac{V_2}{I_1\times L_c}$$

(1)

그림 1. | Fig. 1. 단일 편조 케이블을 포함한 triaxial 케이블의 구조 | Structure of triaxial cable including single braided cable.

Download Original Figure

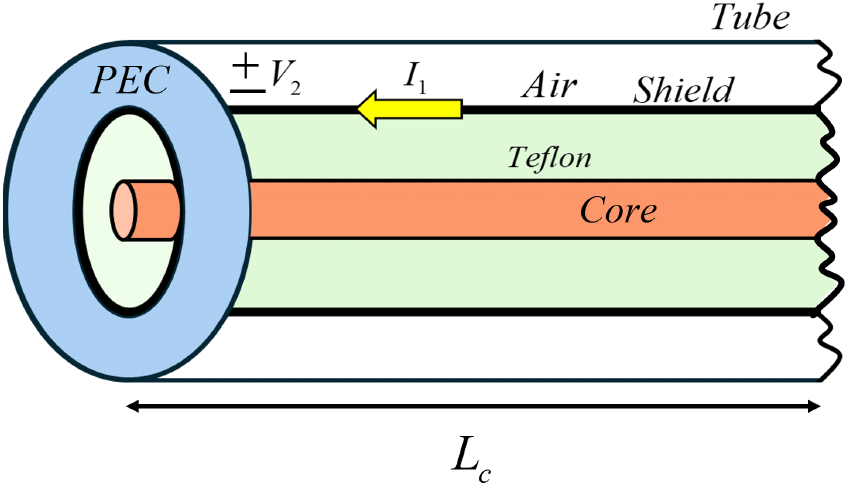
전압, 전류비로 구한 단위 길이당 전달 임피던스로 케이블의 차폐 정도를 판단할 수 있다. 케이블 쉴드층에 흐르는 전류는 공급 전류로 일정하며, 외부 도체로 유도되는 전압이 작을수록 단위 길이당 전달 임피던스가 작아진다. 이는 케이블의 차폐가 잘 되고 있다는 것으로 해석할 수 있다.

2-1-1 Triaxial 방법의 등가 회로

Triaxial 방법은 케이블의 중심 도체, 쉴드, 외부 튜브로 이루어져 있고, 전체 모양이 케이블을 포함한 케이블의 형태와 모양이 비슷하여 삼축 방법이라고 부르며 케이블의 쉴드층과 측정 장치의 외부 도체 사이에 폐루프를 형성시켜 전달 임피던스를 측정하는 방법이다. EN 50289와 IEC 62153은 공통적으로 Triaxial 방법을 이용하지만 EN 50289는 케이블 내부에 전류를 흘려주어 외부 도체로 유도되는 전압을 측정하는 방식이고, IEC 62153은 케이블 쉴드를 기준으로 내부 도체로 유도되는 전압을 측정하여 전달 임피던스를 구하는 방식의 차이가 존재한다. EN 50289와 IEC 62153은 전류 소스의 위치 차이가 반대인 것으로 정리할 수 있다. 그리고 IEC 62153의 경우 외부 튜브 구조의 특성 임피던스를 고려해야 하지만 EN 50289의 경우 외부 도체의 크기에 상관없이 설계/제작이 가능하다.

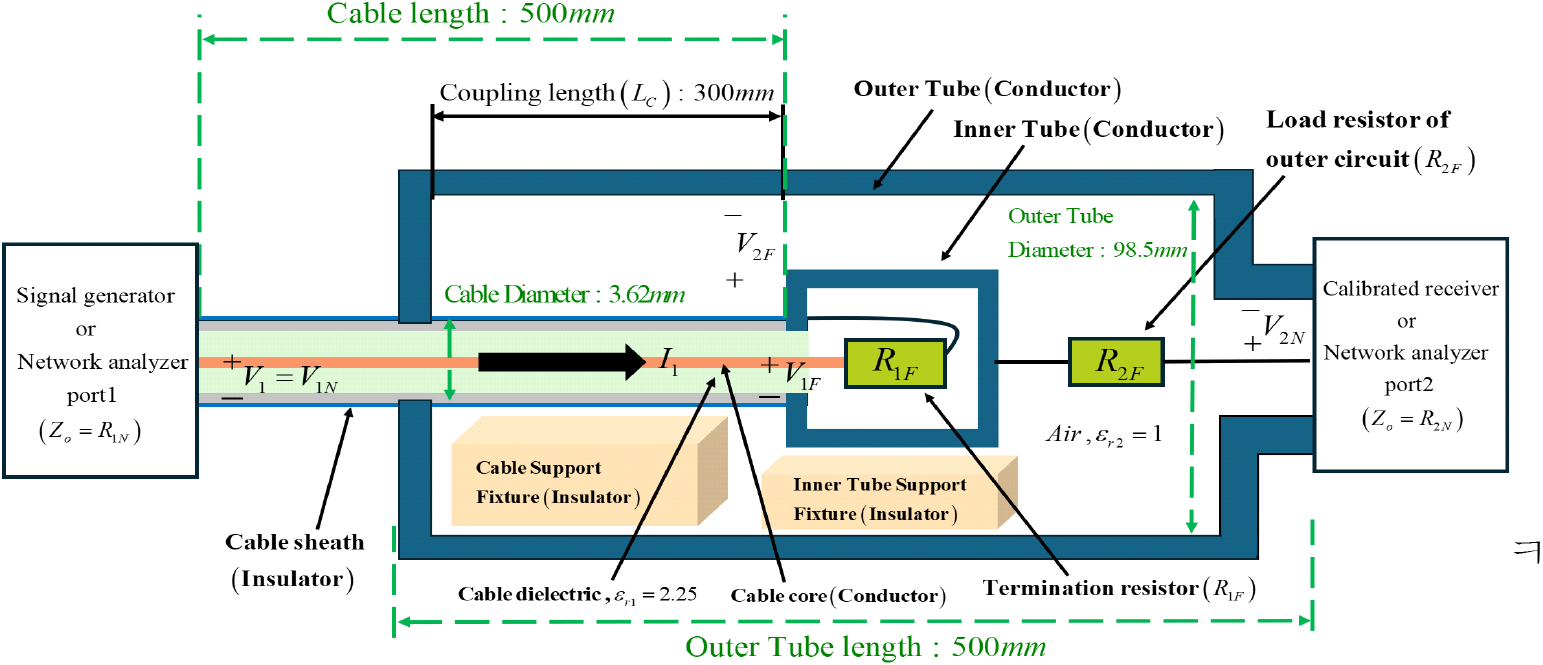
본 연구에서는 EN 50289를 기반으로 케이블의 전달 임피던스를 측정하는 장치를 설계/제작하였다. 사용한 RF 케이블은 RG 402이고, 측정 장치는 그림 2와 같다. EN 50289 규격에서 커플링 되는 단위 길이당 전달 임피던스를 집중 소자로 표현하기 위해 결합 길이를 파장의 1/10정도로 작게 하였다. 이에 따라 파장과 주파수의 관계에 의해 최대 주파수 100 MHz에 대한 측정 결합 길이는 0.3 m이다. 그림 2의 측정 구성도는 참고문헌 [6]을 참고하여 재구성하였다. Triaxial 방법의 전달 임피던스를 구하기 위해 측정 구성의 등가 회로는 그림 3으로 표현할 수 있으며, 사용된 변수에 대한 설명은 아래와 같다. 변수 표기에서 N(near)과 F(far)는 측정 포인트를 기준으로 산정하였다.

V_1N: 내부 회로의 입력전압

V_2N: 케이블 쉴드를 기준으로 외부 도체로 유도되는 전압

R_1F: 내부 회로의 종단 저항

R_2F: 외부 회로의 로드 저항

R_1N, R_2N: 회로망 분배기 내부 저항 50 Ω

그림 2. | Fig. 2. Triaxial 방법의 구조 | Structure of triaxial method.

Download Original Figure

그림 3. | Fig. 3. Triaxial 방법의 등가 회로 | Equivalent circuit of triaxial method.

Download Original Figure

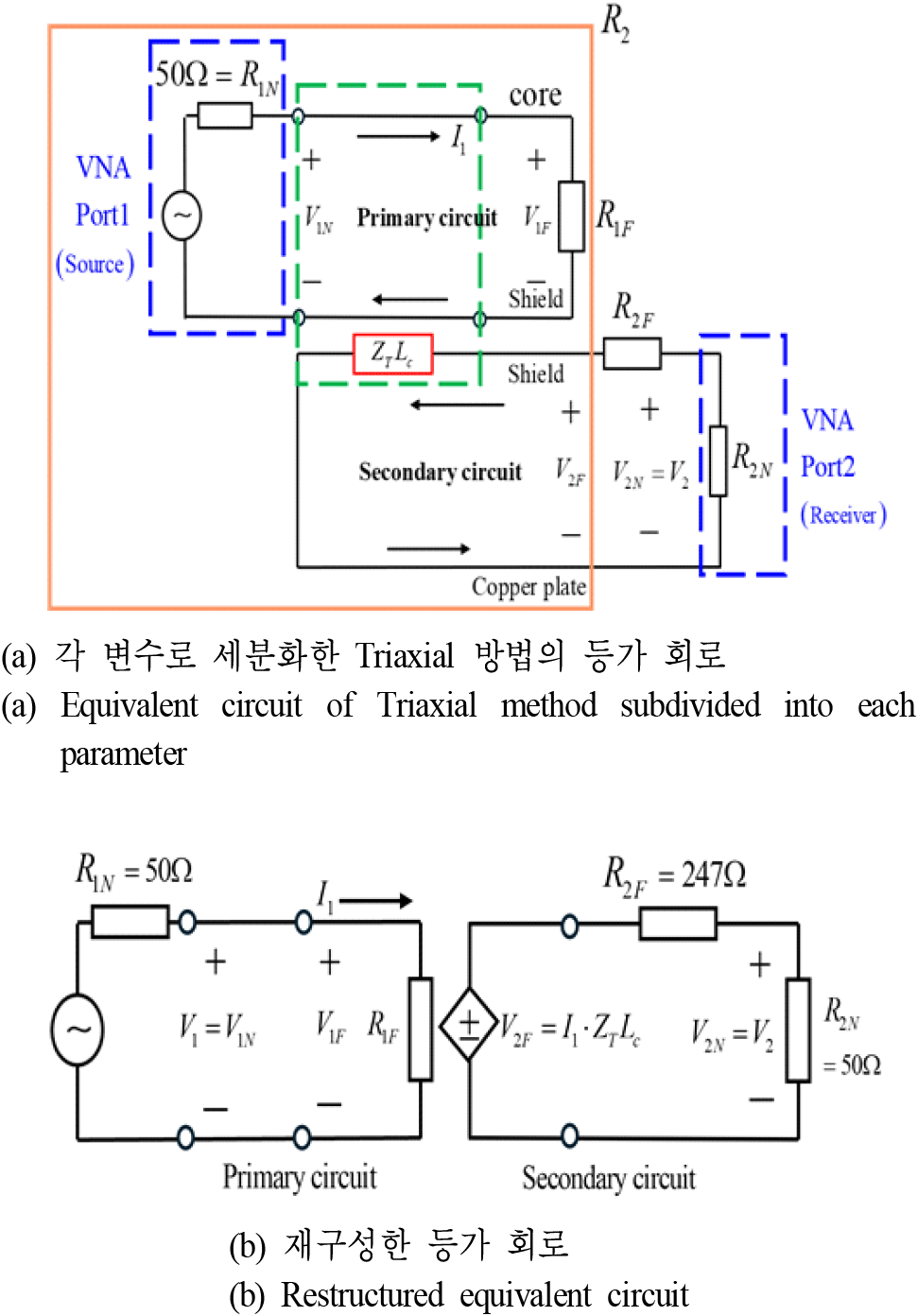
그림 3(a)는 테스트 셋업의 등가 회로이고, 그림 3(b)는 재구성된 등가 회로로 그림 3(a)와 구성은 같지만 간단하게 전압원 V_2F를 통해 단위 길이당 전달 임피던스 수식을 유도할 수 있다. 해당 수식은 내부 회로와 외부 회로에서 사용한 변수들의 간단한 회로 수식과 그림 4를 통해 측정되는 S 파라미터를 포함하여 식 (2), 식 (3) 및 식 (4)를 얻을 수 있다^[6].

$$V_{2F}=\frac{R_{2N}+R_{2F}}{R_{2N}}{V}_{2N}$$

(2)

$$I_1=\frac{V_{1N}}{R_{1F}}$$

(3)

$$\begin{array}{cc}{Z}_T& =\frac{V_{2F}}{I_1{L}_c}=\frac{\frac{R_{2N}+R_{2F}}{R_{2N}}{V}_{2N}}{\frac{V_{1N}}{R_{1F}}{L}_c}\\ & =\frac{R_{1F}\left(R_{2N}+R_{2F}\right)}{R_{2N}{L}_c}\frac{V_{2N}}{V_{1N}}\\ & =\frac{R_{1F}\left(R_{2N}+R_{2F}\right)}{R_{2N}{L}_c}{10}^{\left[\frac{S_{21(dB)}}{20}\right]}\end{array}$$

(4)

그림 4. | Fig. 4. Triaxial 방법의 측정 셋업 | Measurement setup of triaxial method.

Download Original Figure

측정 전압 $V_1=V_1^{+}(\text{입사})+V_1^{-}(\text{반사})$로 정의되고, 포트 1에서 회로를 바라본 입력 임피던스는 50 Ω으로 정합되어 있어 포트 1에서 $V_1^{-}=0\text{으로}{V}_1=V_1^{+}\text{으로}$ 수 있다. 따라서 전달 임피던스는 S 파라미터를 사용하여 계산할 수 있다.

2-1-2 Triaxial 방법 구성도의 변수값

광대역으로 사용 가능한 일반 케이블의 경우 내부 종단 저항 R_1F는 50 Ω이지만, 전력용 케이블의 경우 참고문헌 [4] 및 참고문헌 [5]와 같이 식 (5)으로 측정을 통해 구할 수 있다.

$$R_{1F}=\sqrt{Z_{open}\times Z_{short}}$$

(5)

케이블과 외부 도체의 로드 저항 R_2F은 참고문헌 [6]과 같이 식 (6) 및 식 (7)로 구할 수 있다.

$$R_2=1.4\times 60\ln \left(\frac{d_o}{d_s}\right)$$

(6)

$$R_{2F}=R_2-50$$

(7)

Triaxial 방법 구성도의 변수값은 표 1과 같이 정리할 수 있다.

표 1. | Table 1. Triaxial 방법 구성도의 변수값 | Parameters of the Triaxial method.

Geometrical parameter	Symbol	Value
Diameter of cable shield	dS	3.62 mm
Diameter of outer tube	dO	98.5 mm
Termination resistor	R 1F	50 Ω
Load resistor of shield	R 2F	247 Ω
Cable length	L	0.5 m
Coupling length	LC	0.3 m

Download Excel Table

Ⅲ. 전달 임피던스 이론 수식

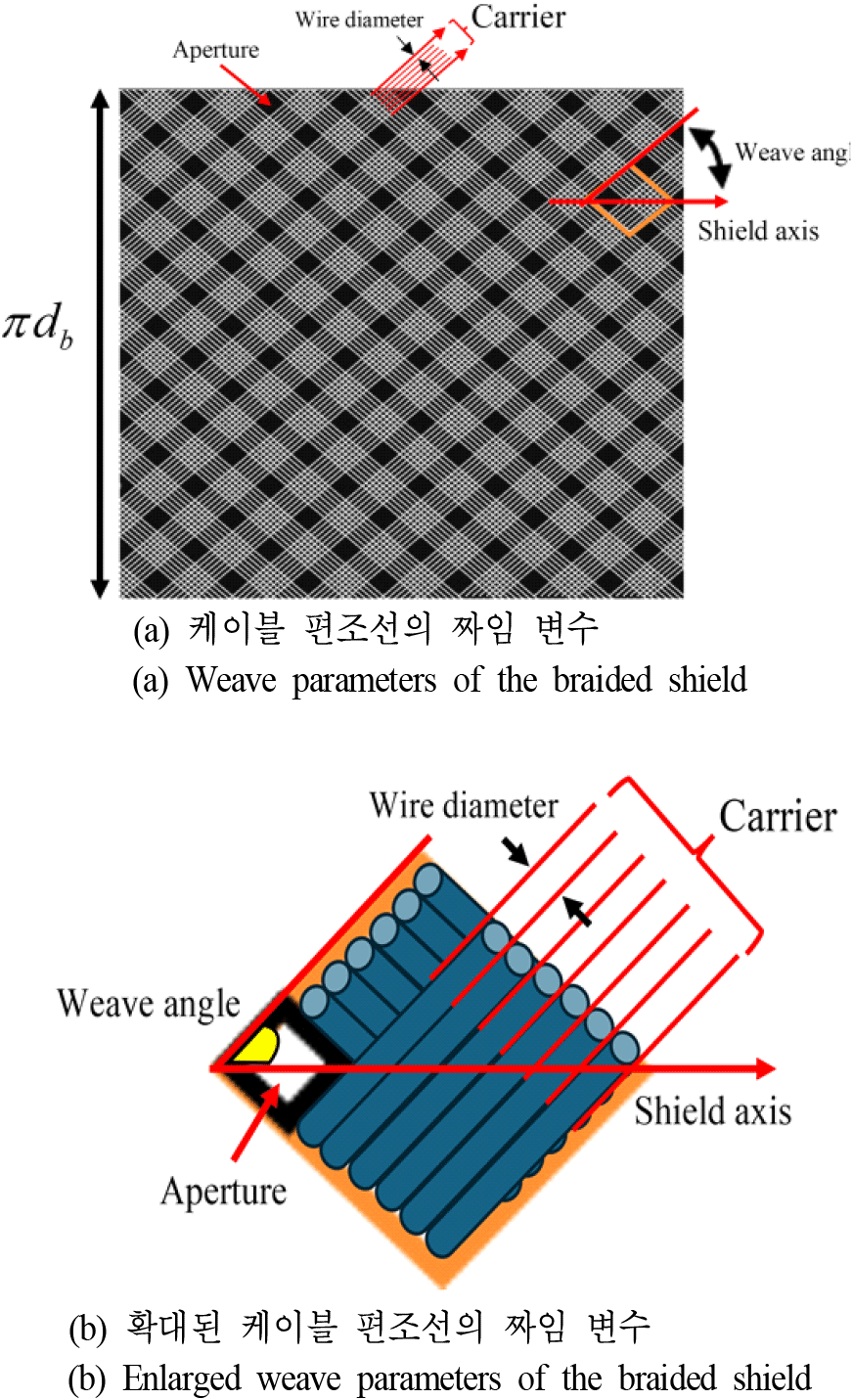
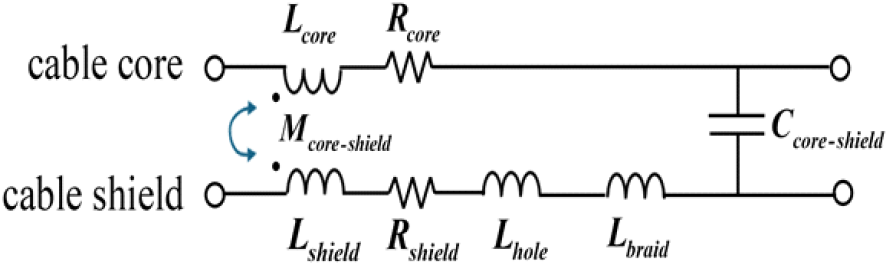
전달 임피던스는 케이블의 구조에서 파생되며 차폐 전류, 외부 자기파, 케이블 내부에서 전파되는 TEM파 (transverse electromagnetic wave) 사이의 결합으로 유도성 결합이다. 따라서 Demoulin의 전달 임피던스 수식은 저항과 인덕터로 구성되며, 표 2의 사용된 케이블의 변수값들로 임피던스와 인덕턴스가 계산된다. 그림 5는 사용한 케이블의 편조선 단면으로 그림 5(a)는 사용한 케이블 편조선의 짜임 변수이고, 그림 5(b)는 확대된 케이블 편조선의 짜임 변수이다. 표 2는 그림 5의 변수값을 정리한 표이다.

그림 5. | Fig. 5. RF RG402 케이블의 편조선 단면 | Cross-section of the braided shield of the RF RG 402 cable.

Download Original Figure

3-1 Demoulin의 모델

참고문헌 [7] 및 참고문헌 [8]에 따르면 Demoulin의 전달 임피던스 수식은 네 가지 항으로 식 (8)과 같이 구성되어 있고, 이론 수식에 대한 케이블의 회로도는 그림 6과 같다.

$$Z_{T,Demoulin}=Z_{diffusion}+j\omega \left(L_{hole}+L_{braid}\right)+k\sqrt{\omega }{e}^{j\frac{\pi }{4}}$$

(8)

그림 6. | Fig. 6. 케이블의 단위 길이당 등가 회로 | Equivalent circuit per unit length of the cable.

Download Original Figure

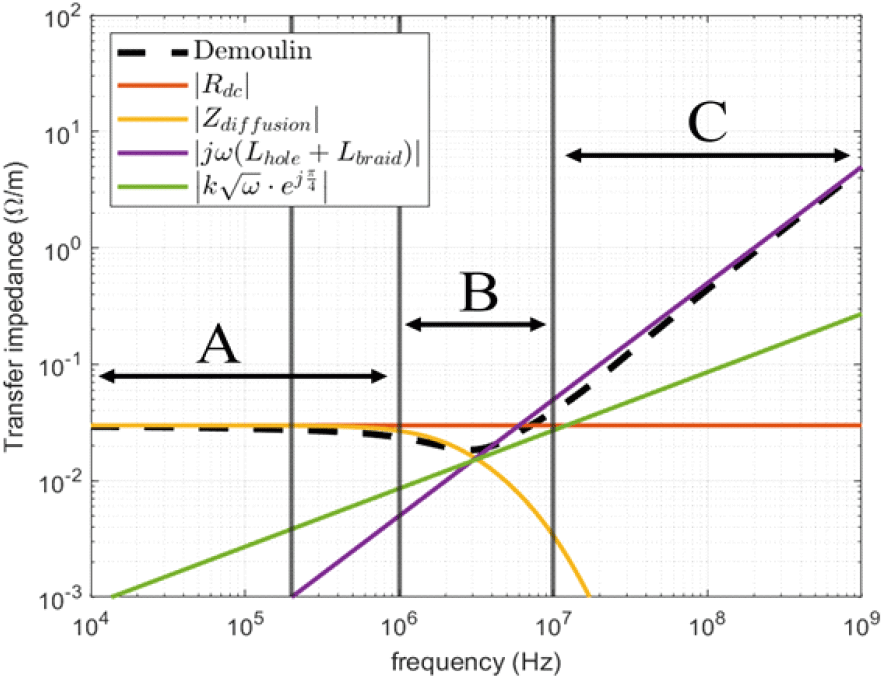
주파수에 따라 각 항의 지배적인 영역이 다르기에 10~1 GHz까지의 전달 임피던스 크기의 그래프로 세 가지 영역으로 나누어 분석을 진행하였으며 그림 7과 같다. 영역 A는 Z_diffusion수식에 의해 R_dc와 표면 효과를 고려한 Z_diffusion 두 부분으로 나뉘어진다. 먼저 200 kHz 전까지는 저주파로 전류 밀도가 고르게 분포하기 때문에 쉴드의 DC 저항값으로 존재한다. 200 kHz~1 MHz는 표면 효과의 영향으로 주파수가 증가할수록 전달 임피던스가 감소하는 경향을 가진다. 영역 B의 주파수 대역인 1 MHz~10 MHz는 쉴드의 와전류 효과로 인해 생기는 Demoulin이 제시한 추가항의 효과가 포함되어 있다. $\sqrt{\omega }$에 비례하는 추가항과 나머지 세 개의 항으로 인해 변곡점이 만들어져 전달 임피던스가 증가하기 시작한다. 영역 C의 주파수 대역인 10 MHz 이후는 hole 인덕턴스와 braid 인덕턴스가 지배적이다.

그림 7. | Fig. 7. Demoulin 이론 수식 모델 구성 요소 | Components of Demoulin equation model.

Download Original Figure

Region A(~1 MHz) : $\left|Z_{\text{diffusion}}\right|$

Region B(1 ~10 MHz) : $\left|Z_{diffusion}+j\omega \left(L_{hole}+L_{braid}\right)+k\sqrt{\omega }{e}^{j\frac{\pi }{4}}\right|$

Region C(10 MHz ~) : $\left|j\omega \left(L_{hole}+L_{braid}\right)\right|$

3-2 구조적 특성이 고려되어 수정된 Demoulin의 모델

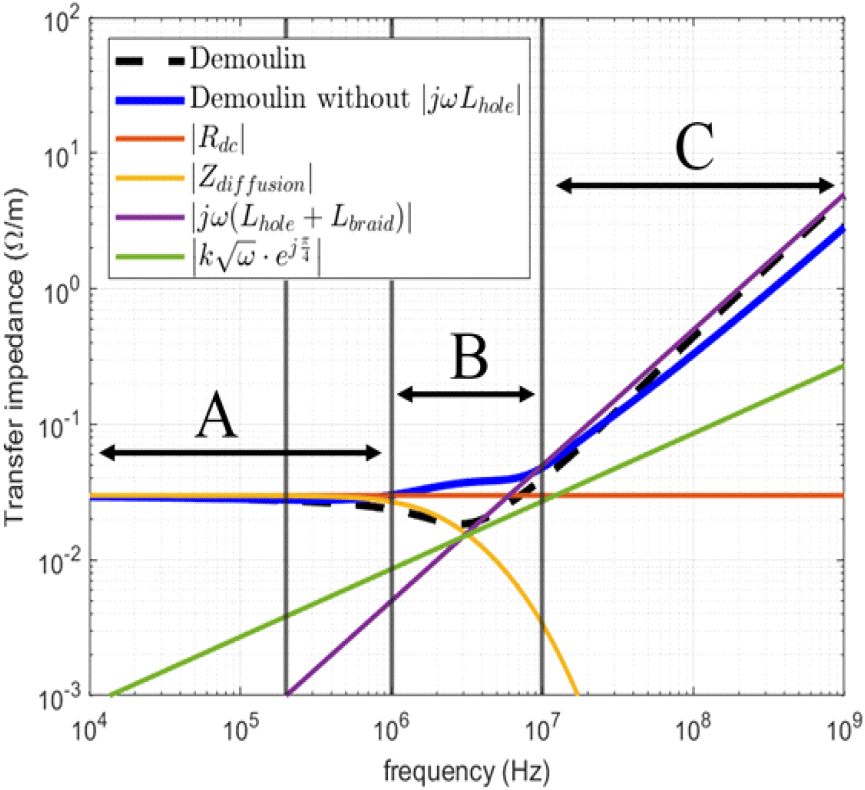
기존의 Demoulin 이론 모델은 케이블 자체의 전달 임피던스에 대한 수식이며 측정 시 사용되는 외부 튜브가 고려되지 않았다. 그리고 Triaxial 방법으로 케이블의 전달 임피던스를 측정 시 정확한 측정을 위해서는 쉴드와 외부 튜브가 빈틈없이 맞닿아 있어야 한다. 이를 다시 해석하면 쉴드와 외부 튜브가 맞닿은 부분은 전위차가 존재하는 하나의 접지로 볼 수 있고, 전체적인 형상은 쉴드 위에 구리로 된 접지가 둘러 쌓여있는 형상이다. 쉴드는 변수값 C인 캐리어가 두 개 교차되어 케이블의 유전체를 나선형 방향으로 감싸는데, 이때 교차된 캐리어들로 인해 아주 작은 다이아몬드 hole이 생성된다. 이 hole을 통해 자기장이 침투되면서 생기는 효과가 L_hole인데, 쉴드 위에 구리 접지로 빈틈없이 붙어있으므로 hole로 침투되는 자기장의 영향력은 없다고 볼 수 있다. 그리고 L_braid항의 경우 쉴드가 케이블 길이에 걸쳐 외부 튜브 내 노출되어 있으므로 무시할 수 없을 것이다. 따라서 구조적 특성의 영향을 많이 받는다고 추측한 L_hole항의 영향을 제외한 단위 길이당 Demoulin의 이론 수식의 수치 해석 결과는 영역 B와 C에서 변화가 생길 것이며, L_hole의 영향보다 L_braid의 영향이 더 크다면 L_braid항이 지배적인 영역 C가 다른 항의 간섭을 받는 영역 B보다 변동이 적을 것으로 예상된다. 참고문헌 [9]에 의하면 α가 45° 이하일 때, 20 k~10 MHz에서 침투하는 자기장의 영향력이 매우 작아 무시할 수 있다고 되어있으며, 일반적인 RF 케이블의 경우 가장 이상적인 각도가 45°이며, 45° 이하의 각도로 제작되므로 L_hole의 영향을 무시할 수 있다.

그림 8은 단위 길이당 Demoulin의 전달 임피던스 이론 수식과 jωL_hole항을 제외한 이론 수식의 수치 해석 결과이다. 검은색 점선이 Demoulin 이론 수식이고, 파란색 실선 이 Demoulin 이론 수식에서 jωL_hole항을 제외한 수식이다. 두 수식은 L_hole항이 포함된 영역 B와 C에서 차이가 나고, 오차는 각 영역의 주파수 포인트에 대한 평균값을 구하여 Demoulin 이론 수식을 기준으로 표 3과 같이 정리하였다. 영역 B에서 약 60.9 %의 차이가 발생하였고, 영역 C에서 12.2 %의 차이가 발생하였다. 예측한대로 영역 C가 B보다 변동이 적은 것을 확인할 수 있다.

그림 8. | Fig. 8. Demoulin 이론 수식에서 L_hole항을 제외한 결과 | The result after excluding the L_hole term from the Demoulin equation.

Download Original Figure

표 3. | Table 3. L_hole 항을 제외한 Demoulin 이론 수식, Demoulin 이론 수식 , 수정된 이론 수식, Triaxial 방법 측정의 오차 비교 | Comparison of error rates between demoulin theory equation without the L_hole term, demoulin theory equation, revised theory equation, and triaxial method measurement.

	Region A (%)	Region B (%)	Region C (%)
The error between the theoretical value excluding Lhole and the theoretical value	0	60.87	12.2
The error between the theoretical value and the measured value	30	34.29	24.24
The error between the revised theoretical value and the measured value	20	2.86	8.33
Error improvement rate	10	31.43	15.91

Download Excel Table

구리 접지에 해당하는 형상은 그림 9와 같고, 표 1의 변수값인 커플링 되는 길이 L_C, 쉴드의 직경 d_s, 그리고 측정에 사용된 외부 튜브의 두께 0.2 mm를 사용하여 ANSYS Q3D를 통해 4 mΩ에 해당하는 R_tube값을 추출하였다. 이때 주파수 범위는 10~1 GHz까지 100 포인트에 대하여 인터폴레이팅을 진행하였다. 수정된 모델은 jωL_hole의 항이 제거되고 R_Tube항이 추가되어 Triaxial 방법으로 측정 시 구조적 특성이 고려된 케이블의 단위 길이당 전달 임피던스 수식은 식 (9)과 같다.

$$Z_{T,\text{revised}}=Z_{\text{diffusion}}+R_{\text{tube}}+j\omega L_{\text{braid}}+k\sqrt{\omega }{e}^{j\frac{\pi }{4}}$$

(9)

그림 9. | Fig. 9. 외부 튜브를 Q3D로 모델링한 형상 | Shape of the outer tube modelde in Q3D.

Download Original Figure

Ⅳ. 측정 및 이론 수식 비교

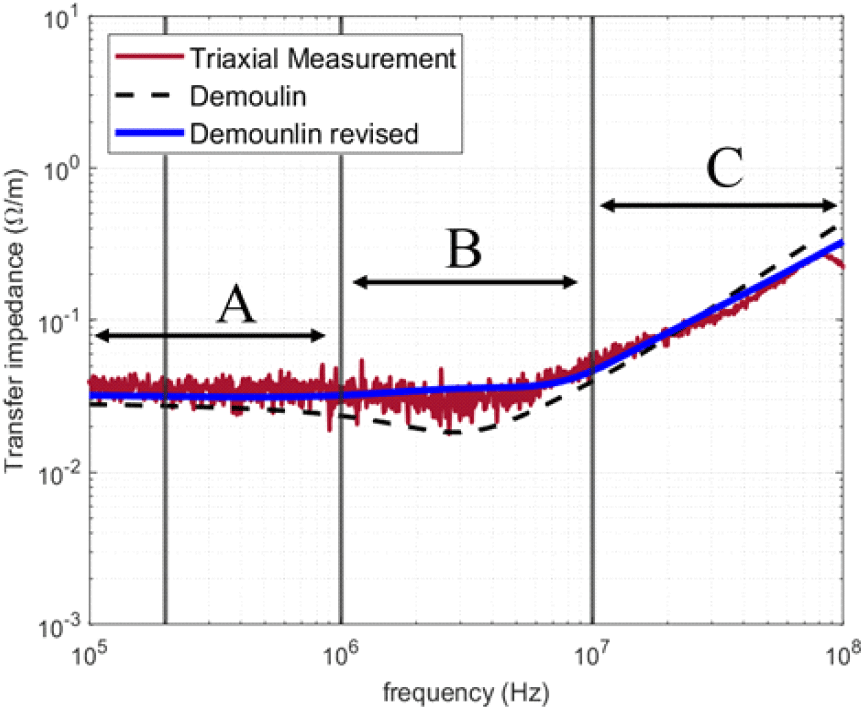
Triaxial 방법의 측정 셋업인 그림 4와 식 (4)를 통해 측정된 Demoulin 이론 수식을 비교한 결과는 그림 10과 같다. 자주색 실선은 Triaxial 방법의 측정값이고, 검은색 점선은 Demoulin의 이론 수식의 수치 해석값, 파란색 실선은 제시한 수정된 Demoulin의 이론 수식의 수치 해석값이다. 전달 임피던스의 값이 매우 작아 각 영역의 주파수 포인트에 대한 평균값을 구하여 측정값을 기준으로 표 3과 같이 오차를 비교하였다. Demoulin 이론 수식은 영역 A는 약 30 %, 영역 B는 34.3 %, 영역 C는 24.2 %의 차이가 존재한다. 수정된 Demoulin 이론 수식은 영역 A는 약 20 %, 영역 B는 2.9 %, 영역 C는 8.3 %로 오차가 감소한다. 따라서 수정된 Demoulin 이론 수식이 전체 영역에서 Triaxial 방법의 구조적 특성이 고려됨을 확인하였다.

그림 10. | Fig. 10. Triaxial 방법 측정, Demoulin 이론 수식, 수정된 이론 수식의 단위 길이당 전달 임피던스 | Per unit length transfer impedance results from triaxial method measurement, Demoulin's theory equation, and the revised theory equation.

Download Original Figure

Ⅴ. 결 론

본 논문은 케이블의 차폐 정도를 판단하는 매개변수인 전달 임피던스가 이론 수식과 측정이 상당 부분 차이가 발생하여 Triaxial 방법의 구조적 특성을 고려하여 이론 수식을 수정하였다. Triaxial 방법을 사용하기 위해 종단 조건, 셋업, 그리고 등가 회로를 제시 후 RF RG402 단일 편조 케이블을 대상으로 전달 임피던스를 측정하였다. Demoulin의 전달 임피던스 이론 수식은 주파수 영역에 대해 분석 후 참고문헌 [9]와 Triaxial의 구조적 특성을 시뮬레이션을 통해 수식을 제안하였다. 그 결과 측정값을 기준으로 수정된 이론적 수식 해석 결과의 오차가 기존의 Demoulin 수식에 비해 영역 A는 약 10 %, 영역 B는 31.4 %, 영역 C는 15.9 % 개선되었다.

결론적으로, 본 논문에서 제시한 수정된 Demoulin의 전달 임피던스 모델은 무겁고 재구성하기 번거로우며 쉴드와 외부 튜브의 접촉이 빈틈없이 이루어져야 하는 Triaxial 방법으로 케이블 전달 임피던스를 측정하지 않고도 수정된 이론 수식 모델을 통해 정확한 전달 임피던스 결과를 예측 가능할 것으로 기대된다.

향후 Triaxial 방법과 비슷한 line injection 및 ground plate 방법에도 하나의 이론 수식으로 비교하는 것은 측정 환경에 대한 구조적 특성을 고려하지 않았기 때문에 측 도 수정된 이론 수식 모델을 통해 정확한 전달 임피던스 결과를 예측 가능할 것으로 기대된다.