Ⅰ. 서 론
최근 전자전의 중요성이 확대됨에 따라 입사되는 전파 신호의 방향을 탐지하는 방향탐지 기술(direction finding)의 수요가 증가하고 있다[1]. 특히, 항공 기술의 발전에 따라, 이동체의 속도가 증가하고 있으며 이러한 초고속 이동체가 방사하는 전파의 방향을 탐지 및 추적하기 위해선 빠른 방향탐지가 요구된다[2]. 모노펄스(monopulse) 알고리즘은 수신된 하나의 펄스 신호만으로 전파의 방향을 추정할 수 있는 기술로, 빠른 방향탐지를 가능하게 한다. 모노펄스 알고리즘은 진폭 비교 알고리즘과 위상 비교 알고리즘으로 나뉘며, 안테나 간의 신호의 합과 차를 이용하여 전파의 방향을 탐지하는 기술이다[3],[4]. 위상 비교 모노펄스 알고리즘은 진폭 비교 알고리즘과 비교하여 노이즈에 보다 강인하다는 장점이 있다. 그러나 위상 비교 모노펄스 알고리즘은 안테나의 배열 간격이 고정되어 있을 경우, 방향 추정(DoA, direction of arrival)을 신뢰할 수 있는 비모호 영역이 주파수에 따라 달라지며, 특히 고주파 대역에서 비모호 영역이 좁아진다는 문제가 존재한다. 특히, 넓은 각도 범위에서 방향 탐지를 할 경우 이러한 문제는 두드러진다. 이러한 방향탐지 추정 모호성을 줄이기 위해, 모노펄스 알고리즘 활용 시 발생하는 DoA 모호성을 최소화하기 위한 시간 변조를 적용한 4D 배열 안테나를 활용한 연구가 있다[5]. 해당 연구에서 DoA 모호성을 줄이기 위해 목표 각도 범위를 여러 구간으로 나눈다. 또한, 신호의 중심주파수를 기준으로 약 1 MHz 대역 내에서 주파수 대역을 각도 구간 수와 동일하게 나누고 4D 배열 안테나를 활용하여 다중빔을 생성한 후, 나눠진 각도 구간에 하나의 빔을 하나의 sideband에서 생성한다. 각 구간 별로 생성된 빔을 활용하여 합-차 패턴을 생성하여 모노펄스 알고리즘 기반 방향탐지를 추정한다. 해당 기술을 활용할 경우, 넓은 각도 범위에서 모호성을 최소화한 방향탐지가 가능하다. 그러나 해당 기술은 광대역 방향탐지 기술이 요구되는 전자전 분야에서 광대역 신호가 입사될 경우, 주파수에 따라 모호성이 생기는 각도 영역이 달라지므로 주파수 별로 구간 분할 조건을 다르게 해야하며, 광대역 신호를 처리하기 위한 시간 변조 구현으로 인해 시스템 복잡성이 증가한다는 단점이 존재한다.
한편, 방향 탐지 모호성을 해결하기 위해, 다른 보조 시스템을 이용한 다중 수신기 시스템을 활용할 수 있다. 보조 시스템을 이용하여 대략적인 신호의 방향을 유추한 후 해당 정보를 기반으로 모노펄스 수신기로 정밀한 방향탐지를 시행하여 방향 탐지 모호성을 줄일 수 있다. 그러나 이러한 방법은 광대역에서 운용 시 고주파수에서 좁아지는 비모호 영역보다 보조 시스템의 방향탐지 정확도가 낮을 경우, 고주파수에서 모노펄스 방향 탐지 정확도가 낮아지며 넓은 각도 범위 내에서 방향 탐지를 해야할 경우 이러한 문제는 두드러진다. 이러한 문제를 해결하기 위해 균일빔 알고리즘이 적용될 수 있다[6],[7]. 균일빔(FIB, frequency invariant beam)이란, 주파수에 따라 동일한 빔패턴을 생성하는 기술로써, 균일빔을 모노펄스 알고리즘에 적용할 경우, 목표로 하는 형태의 합패턴과 차패턴을 광대역에서 균일하게 생성할 수 있다. 따라서, 광대역에서 균일하고 넓은 합패턴과 차패턴을 생성하여 넓은 비모호 영역을 확보할 수 있다. 그러나 기존 연구들은 목표 패턴 생성과 그에 따른 방향 탐지 성능 분석이 제시되지 않거나[6], 균일빔을 적용하기 위한 가중치를 도출하기 위해서 SRV(spatial response variation)와 같은 최적화 알고리즘을 활용한다[7]. 최적화 기반의 알고리즘을 활용할 경우 정교한 균일빔 생성이 가능하나, 목표 패턴의 조건이 복잡할수록 최적화 시간이 많이 소요된다는 단점이 있다. 본 연구에서는 균일빔 생성을 위해 DFT(discrete Fourier transform) 기반의 균일빔 생성 기법을 활용하였다[8]. DFT 방식의 경우, window 함수들을 활용하여 다양한 목표 패턴 생성을 할 수 있으며 목표 패턴의 형상과 관계없이 균일빔 가중치를 빠르게 도출할 수 있다는 장점이 있다. DFT 기반의 균일빔을 활용하여 모노펄스 방향탐지를 시행하기 위해 목표 패턴을 선정 및 생성하고 이를 기반으로 균일빔 가중치를 도출하였으며 균일빔을 반영하기 위해 모노펄스 방향 탐지 추정 수식을 재구성하였다.
본 논문의 구성은 다음과 같다.Ⅱ장에서 신호 모델링 및 기존의 위상 비교 알고리즘 이론에 대해 설명하고, 광대역에서의 방향탐지 성능을 분석하였다. Ⅲ장에서는 균일빔을 적용하기 위해 균일빔 가중치 생성 이론을 설명하고, 균일빔 알고리즘을 반영한 위상 비교 모노펄스 알고리즘 수식 설명 및 광대역 방향탐지 성능을 분석하였다. Ⅳ장에서는 다중 시스템으로의 확장 및 운용 시나리오 예제를 제시하고, 그에 대한 방향탐지 성능을 분석하였다.
Ⅱ. 위상 비교 모노펄스 알고리즘
배열 안테나의 방향탐지 성능을 분석하기 위해서 입사 신호 모델링을 하였다[9]. 특정 각도 θ에서 입사하는 평면파 신호에 의한 배열 안테나의 응답을 나타내는 조향 벡터(steering vector)는 식 (1)과 같이 나타낼 수 있다.
이때 M은 배열 안테나 소자 수를 나타내며, T는 전치행렬을 나타낸다. 또한 φ는 위상차이를 나타내며 이는 식 (2)에서와 같이 나타낼 수 있다.
이때 λ는 파장을 나타내고, d는 배열 안테나 간격을 나타내며, i는 배열 소자 index로, 1부터 M 사이에서 자연수를 가진다. 입사 각도가 θinc일 때, 배열 안테나의 입력 신호 벡터 x는 식 (3)로 나타낼 수 있으며,
이때 s는 신호의 세기이고, n은 배열 소자별 noise를 나타내며, 각 벡터들의 차원은 M×1을 가진다. 배열 안테나의 output 신호 S는 식 (4)와 같이, 입력 신호 벡터 x와 배열 안테나의 가중치 벡터 w의 각 항들은 곱 및 합하여 나타낼 수 있다.
이때 H는 켤레 전치 행렬을 의미하는 에르미트 행렬을 나타낸다. 방향탐지를 위한 가중치 벡터 w는 활용되는 알고리즘에 따라 결정되며, 일반적으로 사용되는 bartlett 빔포머의 경우, 식 (5)와 같이 조향 벡터로 결정될 수 있다.
이번 장에서 배열 안테나의 output S 신호를 활용하여 위상비교 모노펄스 방향탐지를 시행하였다. 위상 비교 모노펄스 알고리즘은 배열 안테나를 활용하여 합신호와 차신호를 활용하여 목표물의 위치를 추정하는 방식이며, 이때 각 안테나로 입사되는 신호의 크기는 같고 위상은 다르다는 특징이 있다[3].
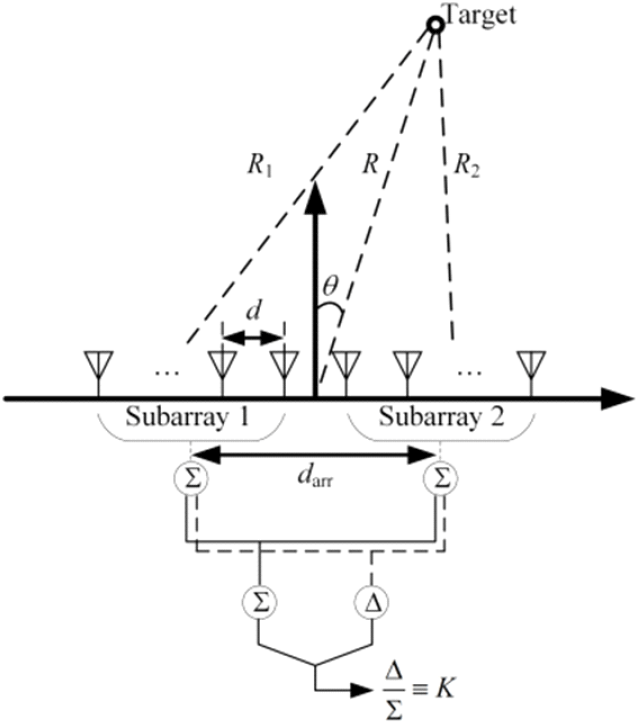
그림 1은 모노펄스 알고리즘 적용을 위한 안테나 및 알고리즘 파라미터에 대한 설명을 나타낸 그림이다. 배열 안테나의 전체 소자 수는 M개이며, 해당 배열을 중심을 기준으로 두 개의 부배열로 나눈다. 이때 각 부배열의 소자 수는 M1, M2으로 M의 절반에 해당한다. 각 부배열들 의 중심 간의 거리를 darr라고 하고, 목표물로부터 배열 중심까지의 거리를 R, 각 부배열의 중심까지의 거리는 R1, R2이다. 목표물과 배열 안테나 사이의 거리가 매우 멀다고 가정할 경우, darr≪R이므로, R1과 R2는 식 (6)과 같이 나타낼 수 있다.
또한 두 부배열 간의 위상 차이 Φ는 식 (7)과 같이 나타낼 수 있으며,
수신된 신호의 합신호와 차신호는 식 (8)과 같이 나타낼 수 있다.
이때, S1과 S2는 각 부배열의 output 신호를 나타내며, n1과 n2는 각 채널에서의 noise를 나타낸다. S1과 S2의 관계는 식 (9)에서 나타낸 것과 같이, 위상 차이 Φ만 존재한다.
합신호와 차신호의 비율 K를 식 (10)에 나타내었으며, noise의 크기가 신호의 크기보다 매우 작다고 가정할 경우, tangent 꼴로 간단하게 나타낼 수 있다.
K가 순허수라고 가정할 경우, 부배열 간의 위상 차이 Φ를 식 (11)과 같이 나타낼 수 있다.
또한 식 (11)을 이용하여 식 (12)과 같이 도래각 θinc를 도출할 수 있다.
광대역에서 위상비교 모노펄스 방향탐지 성능을 나타내기 위해, 본 연구에서 활용한 전체 배열 소자수 M은 16소자로 가정하였다. 각 부배열들은 8소자로 구성되며 배열 간격은 8.9 mm, darr는 71.2 mm인 선형 배열 안테나를 가정하였다. 또한 입사 신호는 6~20 GHz의 광대역에서 존재하고, 하나의 빔으로 ±30° 영역을 탐지하는 것을 목표로 가정하였다.
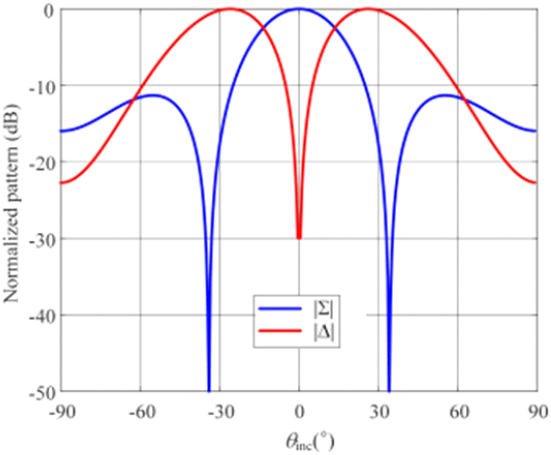
기존의 위상 비교 모노펄스 방향탐지 알고리즘을 활용하여 입사각 추정(DoA, direction of arrival)을 시행하였으며, 정면을 지향할 경우, 입사각도에 따른 합신호와 차신호의 정규화 패턴을 그림 2에 나타내었다. 합신호의 패턴과 차신호의 패턴은 주파수에 따라서 다른 패턴을 나타내는 것을 확인할 수 있다. 합패턴은 고주파로 갈수록 빔폭이 좁아지며, 차패턴은 peak 간의 간격이 줄어든다.
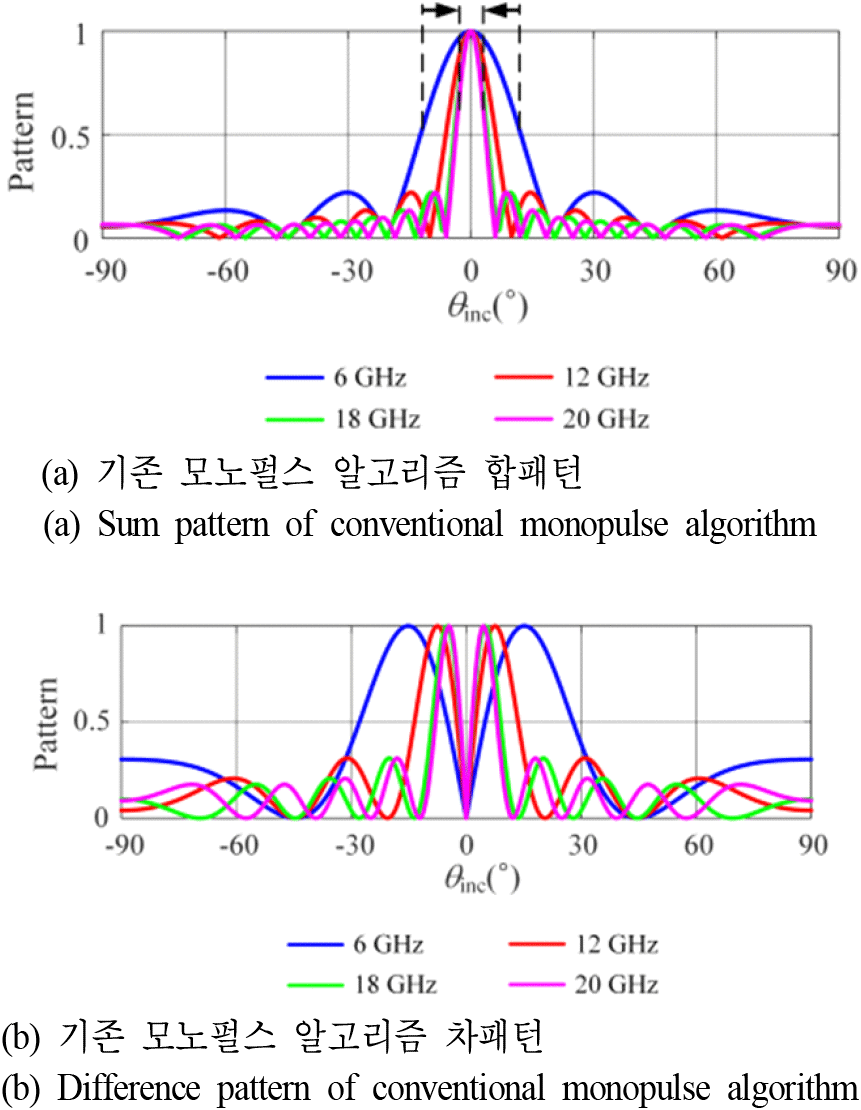
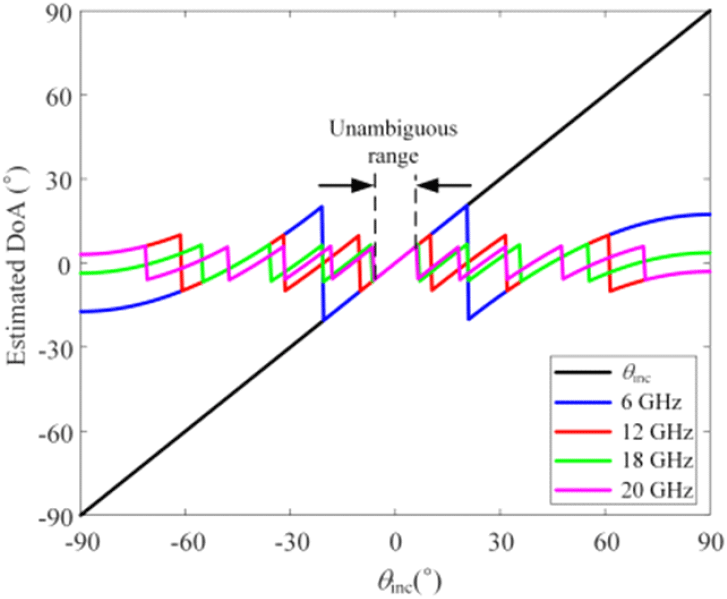
그림 3은 그림 2의 합신호와 차신호 데이터를 기반으로 식 (12)를 활용하여 입사각도에 따른 입사각을 추정한 결과이다. 그림 3에 나타낸 검은색 선은 입사각 θinc과 DoA가 동일한 경우를 나타내며, 검은색 선과 일치하는 영역이 넓을수록 비모호 영역(unambiguous range)가 넓은 것을 나타낸다. 그림 3에서는 주파수에 따라 다른 비모호 영역을 가지는 것을 확인할 수 있으며 주파수가 높을수록 비모호 영역이 감소한다. 특히 20 GHz에서 12°로, 매우 좁은 비모호 영역을 가진다. 주파수마다 다른 비모호 영역으로 인해 빔 운용이 복잡해지며, 좁은 비모호 영역은 방향탐지 효율이 떨어뜨린다. 이러한 문제를 해결하기 위해 주파수 균일빔 알고리즘 적용이 요구된다.
Ⅲ. 균일빔 기반 위상 비교 모노펄스 알고리즘
균일빔을 생성하기 위해 우선 균일하게 생성하고자 하는 목표 패턴 설정이 요구된다. 목표 패턴을 생성하기 위해서 bandpass filter 형태의 식 (13)을 활용하였다.
이때 h는 filter의 계수를 나타내며, h에 따라 패턴의 형상이 결정되므로 목표 패턴을 생성하기 위해서 적절한 값이 선택되어야 한다. 적절한 h를 도출하기 위해, window 함수가 활용될 수 있으며, 본 연구에서는 MATLAB에 내장 함수인 Taylor window 함수를 활용하여 h를 도출하였다. 또한 ω는 각주파수를 의미하며, Mtgt는 filter의 크기, mtgt는 filter index를 나타낸다. 또한 Δxtgt는 filter 간격을 나타내며, x축을 따라 무한한 안테나 소자가 있다고 가정하면 빔 응답 B(ω,θ)는 식 (14)에서와 같이 FIB 가중치 D(mΔx, ω)와 지수함수 형태의 위상 항들과의 합으로 표현할 수 있다.
이때 m은 안테나 index를 나타내고, Δx는 안테나 간격을 나타낸다. 또한 (ω/c)Δxsinθ를 ω1로 치환할 경우, 빔응답은 식 (15)와 같이 DFT(discrete Fourier transform) 형태로 나타낼 수 있다.
FIB 가중치 D(mΔx, ω)는 식 (16)과 같이 개의 주파수 샘플에 대하여 IDFT(inverse discrete Fourier transform)를 적용하여 구할 수 있다.
이때 ω1는 에 대하여 로 나타낼 수 있다. 또한, 식 (16)에서의 D의 차원은 이며 은 안테나 소자 수(M)보다 더 크므로, 배열 안테나에 적용하기 위해 배열 소자 수와 차원 일치가 요구된다. 따라서 D에 적절한 window 함수를 적용해야하며, 본 연구에서는 rectangular window를 활용하였다. 따라서 windowing 이후의 균일빔 가중치 D의 차원은 이며 계산된 균일빔 가중치를 활용하여 균일빔을 생성한다.
균일빔을 생성하기 위해서 본 연구에서 활용한 예제 목표 패턴은 ±30° 영역 내에서 모호 영역을 억제하기 위해 합패턴의 null이 ±30° 내에 발생하지 않고 차패턴의 최댓값이 ±30° 이외에서 나타나도록 선정하였다. 이를 위해 식 (13)의 filter 파라미터를 조정하여 적절한 목표패턴을 생성하였다. 적절한 목표 패턴을 도출하기 위해 Mtgt는 4, Δxtgt는 0.446 λ, h는 [1 1 1 1]인 패턴을 활용하였으며, 이를 기반으로 생성한 합패턴과 차패턴을 그림 4에 나타내었다.
앞서 도출한 D를 위상 기반 모노펄스 방향탐지 반영하기 위해 식 (17)과 같이 output 신호 S를 생성하였다.
이때, D1은 가중치 D 중, 특정 주파수에서의 부배열 1에 해당하는 가중치를 의미하며 차원은 M1×1를 가진다. D2는 D1과 동일하게, 특정 주파수에서의 부배열 2에 해당하는 가중치를 가지고, M2×1 차원을 가진다. 또한 방향 추정 시 균일빔 알고리즘을 반영하기 위해, 각도 방향 추정 식 (12)를 식 (18)과 같이 수정하였다.
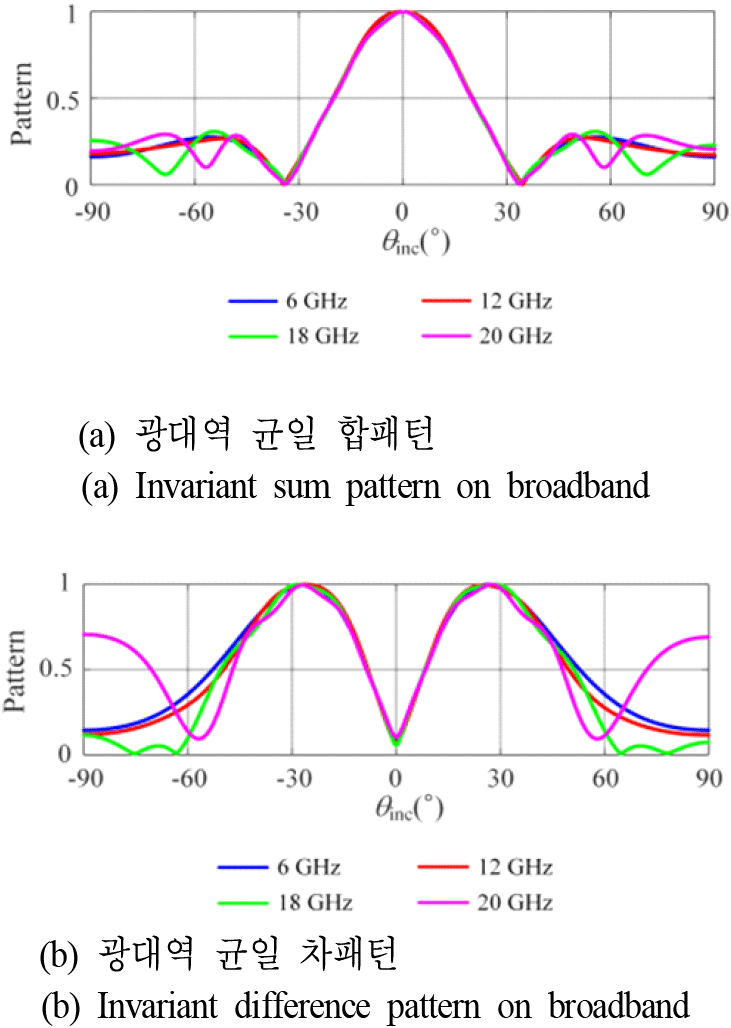
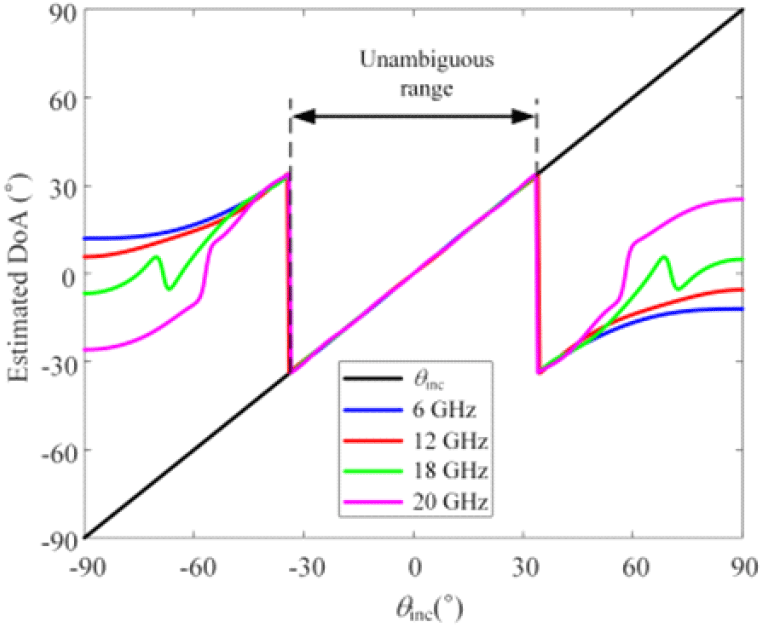
그림 5는 정면을 지향한 경우, 균일빔을 적용한 광대역 합패턴과 차패턴을 나타낸 그래프로, 주파수에 따라 패턴이 변화하는 그림 2와 다르게, 광대역에서 주파수에 따라 유사하며 특히 ±30° 영역 내에서 패턴 간 오차가 매우 적은 것을 확인할 수 있다. 그림 5의 합패턴과 차패턴을 기반으로, 입사 신호 각도에 따른 방향 추정 결과를 그림 6에 나타내었다. 광대역 방향 추정을 시행한 결과, 비모호영역이 광대역에서 ±30° 이상을 유지하는 것을 확인할 수 있다. 모노펄스 수신기 성능을 분석하기 위해 ±30° 범위 내에서 방향탐지 성능을 분석하였다. SNR(signal to noise ratio)이 20 dB인 전파 신호가 입사할 때의 신호의 방향을 추정하였으며, 추정 오차는 RMSE(root mean square error)로 나타내었다. 이때 RMSE는 식 (19)를 활용하여 분석하였으며,
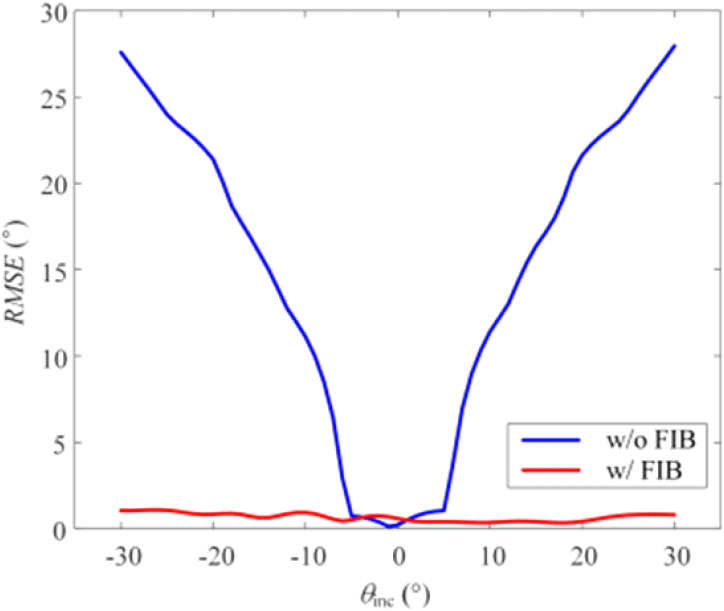
이때 주파수는 6~20 GHz 범위에서 0.1 GHz 단위로 분석하여 는 141개를 가진다. 입사각도 별 RMSE를 그림 7에 나타내었으며, 입사각도는 ±30° 각도 범위 내에서 1° 간격으로 나타내었다. 방향탐지 성능 분석 결과, 균일빔을 적용한 모노펄스 알고리즘은 최대 1.04°의 RMSE값을 가진다. 따라서, 균일빔 기반의 모노펄스 알고리즘을 활용할 경우, 광대역에서 넓고 균일한 비모호 영역 확보로 인하여, 하나의 빔으로 넓은 영역을 탐지할 수 있으며, 주파수에 독립적으로 방향탐지 운용이 가능하므로, 운용 시스템을 간소화할 수 있다.
Ⅳ. 다중시스템을 활용한 방향탐지 성능 분석
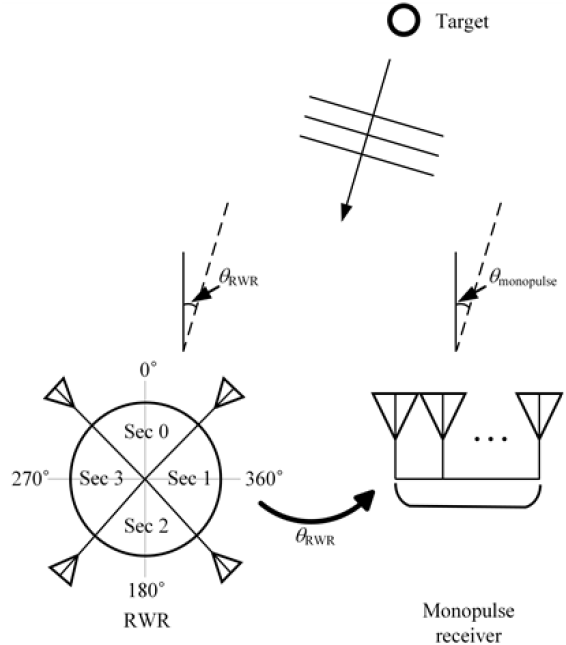
Ⅲ장에서는 제안된 알고리즘을 활용하여 단일시스템으로의 방향탐지 분석을 진행하였다. 추가적으로 다중시스템으로의 확장 가능성을 분석하기 위해 그림 8에 나타낸 것과 같이 RWR(radar warning receiver) 시스템을 활용하여 방향탐지 성능을 분석하였다. 다중시스템을 활용한 방향탐지 성능을 분석하기 위해 시나리오를 생성하였다. 신호는 ±45°내에서 1° 단위로 입사된다고 가정하였으며, 각 입사각에 따라 입사 방향을 추정하였다. 본 논문에서는 정밀한 방향탐지를 위하여 두 단계의 시나리오를 제시한다. 일반적인 RWR 시스템은 10°~15°(RMS, root mean square) 이내의 방향탐지 정확도를 바탕으로 방향을 1단계 추정한다. 1단계에서 추정된 대략적인 방향 정보를 기반으로, 균일빔 모노펄스 수신기를 활용하여 보다 정확한 신호의 방향을 2단계 탐지한다. 이때 균일빔 모노펄스 수신기는 시스템의 복잡성을 낮추기 위해 [−30° 0° +30°]으로 세 방향으로만 빔을 조향하며, RWR이 대략적으로 신호의 방향을 전달할 경우, 신호의 방향과 가장 가까운 방향으로 빔을 조향한다. 가령 RWR로부터 신호가 +40° 방향으로 입사된다고 전달받을 경우, +30°으로 빔을 조향하여 보다 정밀한 방향을 탐지한다. 방향탐지 성능은 RMSE로 나타내었으며, 입사 신호 방향에 따라 그림 9(a)에 나타내었다. SNR이 낮을수록 방향탐지 오차는 증가하는 경향성을 나타내며, SNR이 2 dB일 때, 최대 10.43°의 RMSE을 가진다. 이는 배열 안테나의 위상 차이를 기반으로 방향을 추정하는 알고리즘이므로 낮은 SNR에서 오차가 존재한다. 하지만 SNR이 클수록 방향탐지 오차는 크게 낮아지며, 20 dB에서 RMSE는 1°이하를 유지한다. 추가적으로 ±45° 이내의 모든 입사각도에서, 주파수에 대한 방향 추정 오차를 식 (20)을 활용하여 RMSEtot를 구하였다.
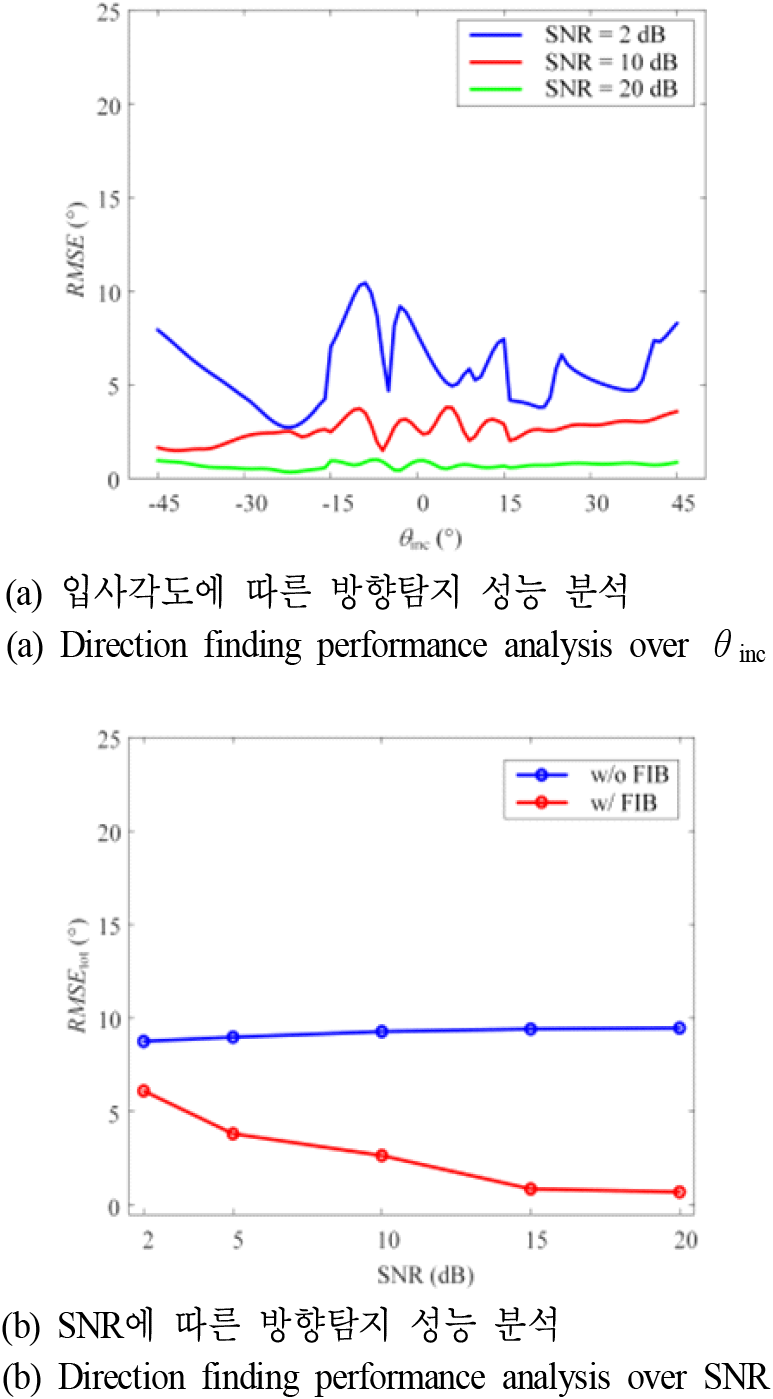
이때 는 시뮬레이션한 총 입사 각도 수이며, ±45°내에서 1° 단위로 할 경우, 91개를 가진다. SNR에 따른RMSEtot를 그림 9(b)에 나타내었으며, 균일빔 적용 전과 적용 후를 비교하였다. 균일빔을 적용하지 않는 경우, 최소 8.76°, 최대 9.47°로 SNR의 크기와 상관 없이 높은 추정 오차를 가진다. 반면, 균일빔을 적용할 경우, SNR이 증가할수록 방향 추정 오차가 급격히 감소하는 것을 확인할 수 있다. 특히, SNR이 5 dB에서 RMSEtot는 3.82°가 되므로, 5° 이내의 오차를 확보하였다. 이를 통해, 다중 시스템을 활용할 경우, 낮은 방향탐지 오차로 넓은 범위의 방향탐지가 가능한 것을 확인하였다.
해당 방향탐지 성능 분석에는 isotropic 방사패턴을 가정하여 분석을 진행하였으나 실제 시스템에는 배열 안테나가 활용되므로, 배열 안테나 간 상호 결합(mutual coupling)을 고려해야 한다. 상호 결합은 수신 신호의 위상 왜곡을 야기할 수 있으며 이로 인해 방향 추정 오차가 증가할 수 있다. 이를 해결하기 위해 알고리즘에 위상 왜곡 보상을 반영하거나 왜곡을 최소화할 수 있는 배열 간격 최적화가 적용될 수 있다. 또한, 배열 안테나 간 상호 결합을 최소화하기 위한 격벽 구조 등을 활용할 수 있다.
Ⅴ. 결 론
본 논문에서는 광대역에서 고속 이동체의 전파 신호 방향을 추정하기 위한 DFT를 활용한 균일빔 기반 다중시스템의 방향탐지 성능을 분석하였다. 다중시스템을 활용하여 방향탐지를 할 경우, 보조시스템의 탐지 오차가 모노펄스 알고리즘의 비모호 영역보다 넓을 경우 방향 탐지 오차가 증가한다. 이를 해결하기 위해, DFT 기반의 균일빔 알고리즘으로 FIB 가중치 D를 계산하였으며, 이를 활용하여, 6~20 GHz 균일빔을 생성하였다. 또한 D를 위상 비교 모노펄스 알고리즘에 반영하여, 광대역에서 균일한 합패턴과 차패턴을 생성하였고, 이를 기반으로 입사각 추정을 시행하였다. 단일 시스템의 경우 ±30° 내에서 비모호 영역을 광대역에서 확보하였으며 SNR이 20 dB일 때, RMSE는 최대 1.04°의 값을 가지는 것을 확인하였다. 또한 다중 시스템을 활용한 방향탐지 성능을 검증하기 위해 방향탐지 시나리오를 제시하였으며, ±45° 내에서 각 방향으로 신호가 입사될 경우, SNR이 5 dB일 때, 3.82°의 방향탐지 오차를 가지며 5° 이내로 방향탐지가 가능한 것을 확인하였다.