Ⅰ. 서 론
RF 수동, 능동 소자의 주파수 응답 특성을 분석하기 위해서 반사계수 측정이 요구된다. 일반적으로 상용화되어있는 VNA(vector network analyzer)의 S-파라미터 측정 장치를 이용하여 수동소자의 반사, 전송 계수를 측정할 수 있으며, 정확한 S-파라미터값을 찾기 위한 오차보상법이 과거부터 많은 연구가 이루어져 왔다[1]~[3]. 그러나 고출력 RF 소스를 이용할 시에 한계점이 존재한다. VNA의 내부 RF 소스는 주로 [mW]급의 소스를 이용하므로 VNA 장비의 전력 제한은 주로 [mW]급으로 설계된다. 따라서 고출력 RF 소스를 이용하는 시스템에서 반사계수 측정을 바로 VNA로 하기에는 무리가 있다.
산업에서 고출력 RF 소스를 이용해 반사계수, 즉 임피던스를 측정하는 시스템이 상용화되어있다. 반도체 플라즈마 공정 중 챔버와 소스간 매칭 상태를 유지하기 위해 전압 - 전류 센서로 임피던스를 측정하는 것이 그 예시이다[4]. 전압 - 전류 센서의 임피던스 측정 원리는 내부의 전압 프로브를 이용해 전압을 측정하고, Rogowski 코일로 전류를 측정해 임피던스를 계산하는 방식이다. 전압-전류 센서를 이용해 임피던스를 측정할 때, MHz대역(수십 meter 단위)의 RF를 수십 cm의 센서에 입력해도 크게 오차를 발생시키지 않기 때문에 임피던스를 측정할 수 있다. 그러나 GHz 대역(수십 cm 단위)의 RF를 센서에 입력하게 되면 오차가 크게 발생하기 때문에 2.45 GHz의 고주파 대역에서는 임피던스 측정이 불가하다.
또 다른 임피던스 측정방법으로 Six-port technique이 알려져 있다[5]. 소스와 DUT(device under test) 사이 4개의 port에서 읽어지는 파워로 임피던스를 계산할 수 있으며 고출력 고주파 RF 파워를 이용해 반사계수 측정이 가능하다. 그러나 VNA의 반사계수 측정 방식에 비해서 상대적 연구결과가 부족하고, 상용화된 장비가 많지 않다.
따라서 본 논문에서는 VNA의 OSL(open, short, load) calibration 방법을 채택하여, 고출력 고주파 RF 소스를 이용해 정확한 반사계수를 측정할 수 있는 시스템을 제안한다. 본 논문의 구성은 다음과 같다. Ⅱ장에서는 circulator와 방향성 커플러로 입사파와 반사파를 분리해 수신하는 회로시스템을 소개하고, 채택한 OSL-calibration의 오차보상 원리와 반사계수를 계산하는 방법에 대해 기술한다. Ⅲ장에서는 설계한 회로 시스템에 대한 시뮬레이션 결과를 보인다. 또한 방향성 커플러의 방향 특성이 좋지 않은 경우에 Circulator를 이용해 특성을 향상시킬 수 있음을 증명한다. Ⅳ장에서는 실제 WR-284 도파관으로 설계한 고출력 동작시스템을 설명한다. 각 커플러에서 수신받은 입사파 반사파 신호처리를 통해 반사계수 측정이 가능함을 보이고, 반사계수 계산 결과를 VNA 측정 결과와 비교하여 오차 범위 내로 일치함을 보인다. 또한, 설계한 시스템의 활용방안을 제시한다. 마지막으로 Ⅴ장에서 결론을 내린다.
Ⅱ. 이론 및 특성 식 유도
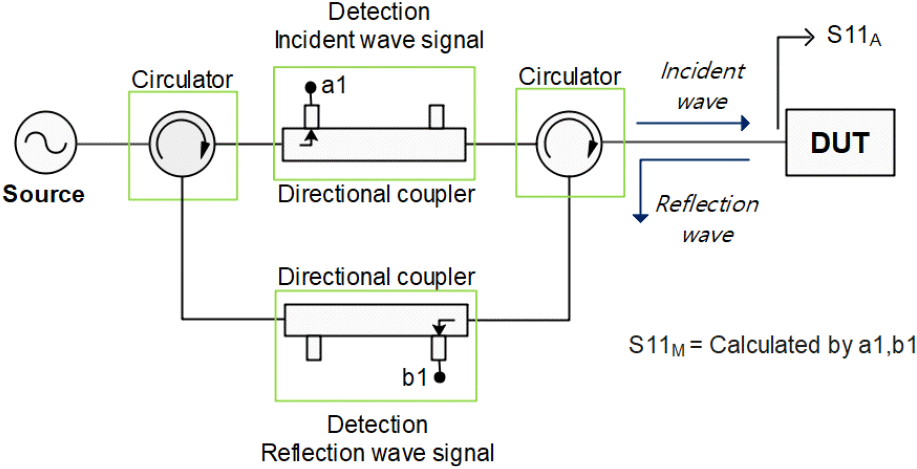
본 논문의 시스템 회로는 RF 소스와 DUT 사이에 2개의 circulator와 2개의 방향성 커플러로 구성되어 있으며 각 커플러에서 입사파와 반사파를 수신하고, circulator로 방향 특성을 향상하는 구조이다. 각 커플러에서 수신한 입사파와 반사파의 비로 반사계수를 구하며 이때 구해지는 반사계수는 DUT 포트 기준이다. 시스템의 구성은 그림 1과 같다. 본 논문의 시스템은 커플러의 방향 특성이 좋지 않은 커플러를 사용해도 반사계수를 정밀하게 측정할 수 있는 장점이 있다.
이때 DUT 포트에서 보이는 반사계수를 구하기 위해서는 calibration을 통한 error term으로 회로시스템의 오차를 보상해야 한다. Error term은 directivity error, source mismatch error, reflection error로 이루어져 있다[6]. directivity error, ED는 방향성 커플러에서 입사파와 반사파의 완전한 분리가 되지 못해 반사신호의 일부가 입사 신호의 수신기로 들어가 발생하는 오차이다. Source mismatch error, ES는 소스포트에서 발생된 신호가 DUT 입력포트로 들어갈 때의 많은 RF 컴포넌트를 거치게 되는데, 각종 RF 컴포넌트, 라인의 커넥터에서 임피던스가 불일치해 발생하는 오류이다. Reflection error, ER은 반사측정 중 test 수신기와 기준 수신기 간 주파수 응답 차이에 의해 발생한다. 따라서 이 3가지 error term을 구해야 반사계수 측정 시 시스템의 오차를 보상할 수 있다. 위의 3가지 error term을 구하기 위해서는 DUT에 3가지의 알려진 기준값을 측정해야 한다. DUT의 실제 반사계수는 S11A이고, 시스템을 통해 ADC에서 바로 측정된 반사계수는 S11M으로 표시된다. 3개의 기준값으로 3개의 연립방정식이 구성되며 그 해를 구하게 되면 error term들을 구할 수 있게 된다. Error term 식은 식 (1)과 같다.
3가지 기준값으로 open, short, load를 이용하여 calibration 시, 각 S11A값이 이상적이다 가정한다면 open일 때 S11A=+1, short일 때 S11A=−1, 그리고 load일 때 S11A=0이다. 이를 적용하여 3개의 error term을 연립방정식으로 푼 결과가 식 (2)~식 (4)이다. 회로시스템에 open, short, load를 연결해 측정되는 반사계수는 각각 , , 로 표현했다. 위에서 계산된 error term으로 S11A을 구해 식 (5)로 임피던스로도 변환할 수 있다.
본 논문의 시스템은 반사계수 S11을 ADC에서 수신된 신호로 계산한다. 전력과 임피던스 관계식을 바탕으로 수신한 입사파 반사파 신호를 S11으로 계산할 수 있다. P는 반사계수의 실수값과 관계되고 식 (6)과 같이 정의한다. Q는 반사계수의 허수값과 관계되고 식 (7)과 같이 정의된다. 이때 입사파를 a1이라 하고 반사파를 b1이라 한다. 각각의 크기는 |a1|, |b1|, 위상은 θa, θb이다. 입사파와 반사파로 구한 P, Q를 통해 위상차와 반사계수를 구할 수 있다. 이를 식 (8) 및 식 (9)에 나타내었다.
따라서 위와 같은 수학적 증명을 바탕으로 S11M을 직접 계산할 수 있게 된다. 위의 계산은 아날로그 신호를 위한 계산법이므로, ADC에서 수신받은 신호는 디지털 신호이기 때문에 디지털 신호 계산법을 적용해야 한다. 이를 식 (10) 및 식 (11)에 나타내었다. 이때 아래 식은 한 주기로 P, Q를 계산하지만 한 주기가 아닌 다른 주기로도 계산할 수 있다.
Ⅲ. 설계 및 검증
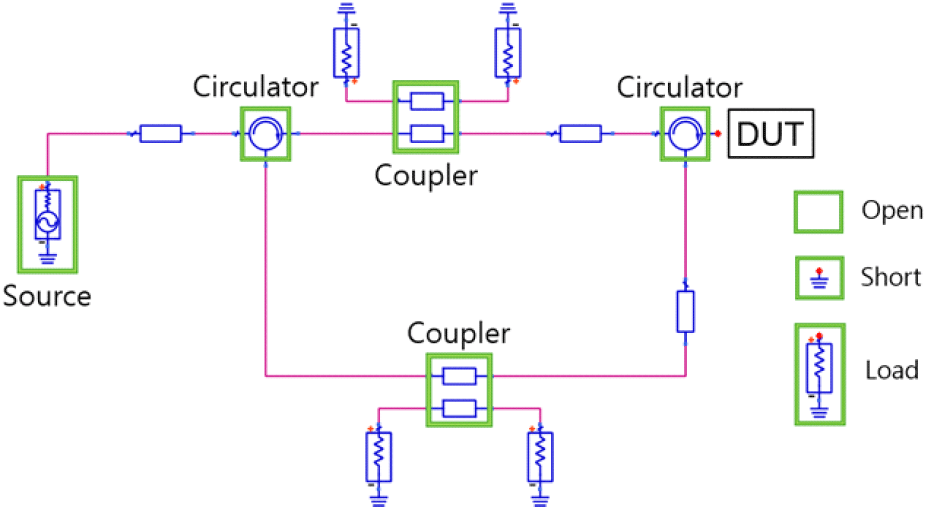
회로시스템을 구현하기 전 ADS[7] 시뮬레이션을 통해 시스템에 오차보상법이 적용되는지 확인하였다. 커플러의 방향성 특성이 낮은 경우에도 시스템이 정상적으로 동작하는지 확인하기 위해 커플러의 방향성 특성을 낮춰 시뮬레이션하였다. 시뮬레이션 변수는 다음과 같다. 소스는 2.45 GHz 0 dBm로 설정하고, circulator는 −15 dB 분리도, VSWR 1, 손실은 0.1 dB로 설정했다. 방향성 커플러의 커플링 계수는 −37.7 dB, 4.5 dB의 방향성, −42.2 dB 분리도로 설정하였으며 전체 ADS 회로도는 그림 2에 나타내었다. Calibration의 open, short, load는 단락과 접지, 50 Ω 저항을 이용했다. 식 (1)의 오차 보상된 S11A를 구하기 위한 error term은 식 (2)~식 (4)를 사용했다. 회로시스템에 오차 보상법이 적용되는지 검증하기 위해 임의의 부하를 테스트했다. 임피던스는 10 Ω 저항, 3 pF 커패시터, 1 nH 인덕터로 설정했다. 회로시스템 DUT에 이 부하를 연결해 측정한 반사계수값과 시뮬레이션에서 측정한 반사계수값을 비교했다. 회로시스템에서 계산된 반사계수값은 −0.650−0.172 i였고, 부하 임피던스의 반사계수 값은 −0.648−0.172 i로 표 1에 각각의 결과를 작성하였다. 각 반사계수의 오차값이 적으므로, 방향 특성이 낮은 회로시스템에서도 오차 보상법이 이론적으로 잘 적용됨을 ADS 시뮬레이션에서 확인할 수 있었다.
| S 11 | Z [Ω] | |
| System result | −0.650−0.172i | 9.94−6.24i |
| Load impedance | −0.648−0.172i | 10−6.26i |
Ⅳ. 실험 결과
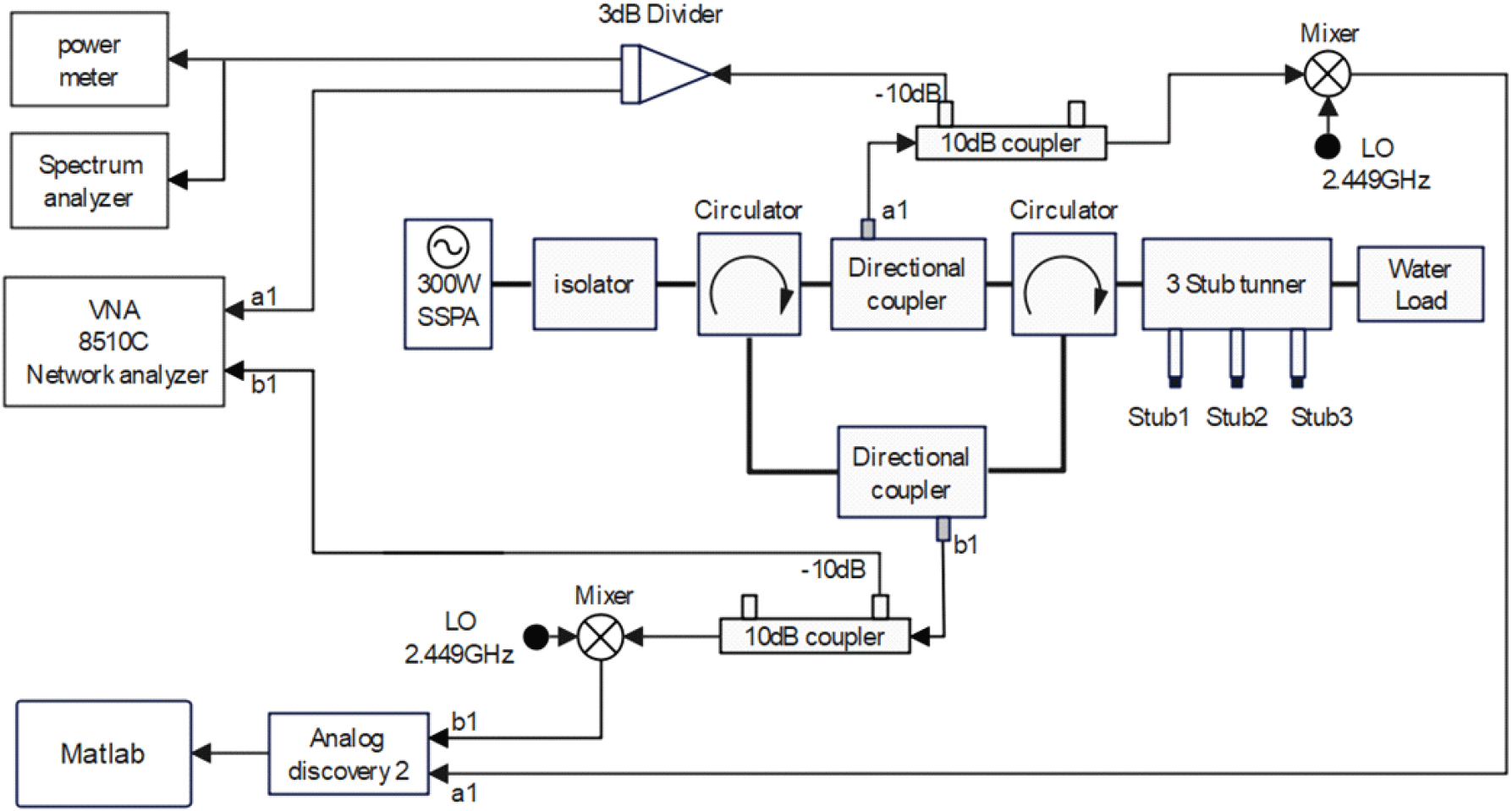
고출력, 고주파 RF 소스를 이용한 반사계수 측정 시스템을 구현하기 위해 WR284 도파관으로 시스템을 구현하였다. 그림 3에 도파관으로 구성한 최종시스템을 나타내었다. 고출력 RF 소스는 NXP사의 MRF24G300H GaN Transistor로 제작된 SSPA 모듈을 이용하였다. SSPA 모듈은 NXP사에서 제공하는 데이터 시트 설계도를 기반으로 제작되었다. 도파관 시스템의 커플러는 커플링 계수가 −40 dB, 방향성 특성이 4.5 dB인 도파관 - 마이크로스트립 라인 커플러를 사용하였고 circulator는 GAE 사의 GA1105 모델(20 dB 분리도)을 사용하였다. 각 커플러의 신호를 10 dB 동축선 커플러로 나눠 Mini circuit사의 ZX05-42MH-S+ 믹서로 1 MHz 하향 변환하여 ADC에 연결하였다. 이때 사용한 ADC는 Digilent사의 ANALOG DISCOVERY 2를 이용했으며 샘플링 속도를 100 Mbps로 설정해 신호를 수신했다. 동축선 커플러의 −10 dB신호는 ADC로 계산된 결과와 비교하기 위해 HEWLETT- PACKARD사의 8510C VNA의 S-파라미터 측정 장비 포트에 연결하여 실험을 진행하였다. 또한, SSPA RF 출력 특성을 확인하기 위해 파워미터와 스펙트럼 측정기에 a1신호를 입력하였다. 파워 미터에서 측정되는 입사파 파워는 251 W, 스펙트럼 측정기에서 측정되는 주파수는 2.45 GHz로, SSPA RF 출력을 유지하며 실험하였다. DUT에 의한 임피던스 변화를 확인하기 위해서 NATIONAL Electronics의 WR284 AI3S 3-stub 튜너를 사용하였다.
Calibration은 도파관 OSL Cal kit을 이용하여 진행하였다. Short는 종단이 금속으로 막힌 WR284 도파관을 이용했고, open의 경우 guided wavelength λg의 1/4 길이로 설계된 WR-284 도파관을 이용하여 종단에 short을 연결해 구현했다. 식 (12)에 의하여 WR-284의 이론적으로 계산되는 λg/4 는 5.77 cm이다. 이때 식 (12)의 λ는 자유 공간에서 파장이고 f는 사용주파수, fco는 차단주파수이다. 실제 제작한 λg/4 도파관은 5.80 cm로 측정되었다. Load는 NATIONAL Electronics의 WR284L OAD6A Water load를 이용해 구현하였다. 이때 VNA를 이용하기 위해, Modify cal 내부 설정이 필요했다. VNA에서 error term 계산 시 open, short, load의 실제 반사계수를 입력시켜야 하므로 설정시 WR-284 도파관의 차단주파수와 90도 지연라인의 electrical delay값을 입력하여 설정하였다.
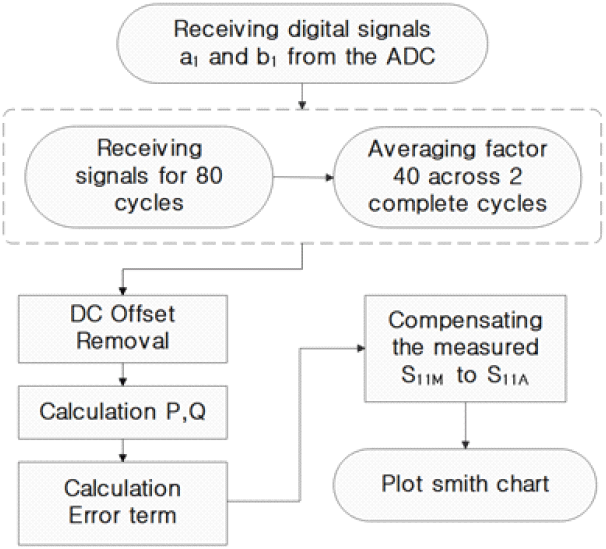
실시간으로 반사계수를 측정, 기록하기 위해 MATLAB으로 프로그램을 작성했다. ADC에서 받은 수신신호를 반사계수로 변환하는 프로그램을 본 논문의 이론 바탕으로 구현하였고, 계산된 값을 smith chart 상에 실시간으로 그리도록 코드를 작성했다. 신호처리 시 노이즈 신호를 줄이기 위해 신호를 총 40번의 평균을 취했으며, 믹서에 의한 DC offset을 제거하는 과정을 거쳤다. 작성한 프로그램 코드는 그림 4에 flow chart로 간략하게 표시하였다.
ADC를 통해 MATLAB으로 계산한 S11값이 정확한 값인지 검증하기 위해 3-stub 튜너의 한 Stub를 하나씩 튜닝하며 총 5곳씩 VNA 측정값과 실시간으로 비교하였다. 그림 5에 VNA와 MATLAB에서 측정된 반사계수값을 Smith chart에 그렸다. VNA에서 측정된 값은 △로 표시하였고 MATLAB 프로그램에서 측정된 값은 ●로 표시했다. 각 Stub별로 튜너의 입력 포트와 가까운 곳부터 Stub1, Stub2, Stub3으로 표시하였다. Stub0의 경우 Stub를 완전히 뺀 상태에서 측정한 반사계수 값이다. 이때 Stub0이 Smith chart 중앙에 위치하지 않는 이유는 Stub가 완전히 빠져도 도파관 안쪽으로 들어와 있어 매칭되지 않기 때문이다. 각 반사계수 측정값의 평균 오차 값은 다음에 명시하였다. 측정된 반사계수의 전체 오차는 실수 값이 0.0233의 평균 오차와 0.024의 표준편차를 가지고 허숫값의 오차는 0.0256의 평균오차와 0.026의 표준편차를 가지게 된다. 프로그램과 VNA의 데이터가 오차를 보이는 이유는 현재 사용한 믹서의 Dynamic range 특성과 Linearity가 VNA의 믹서보다 좋지 않기 때문으로 추정된다. 또한 ADC 성능이 ±25 V, 14 bit로 3 mV의 낮은 전압 해상도를 가지기 때문에 200 mV를 측정하기에는 해상도 특성이 좋지 않고, 또한 노이즈 변동에 의한 오차영향이 존재한다고 추정된다. 그러나 수용할 수 있는 오차 범위 내에 프로그램 계산 값이 존재함으로 설계한 고출력 동작시스템이 잘 동작함을 증명하였다.
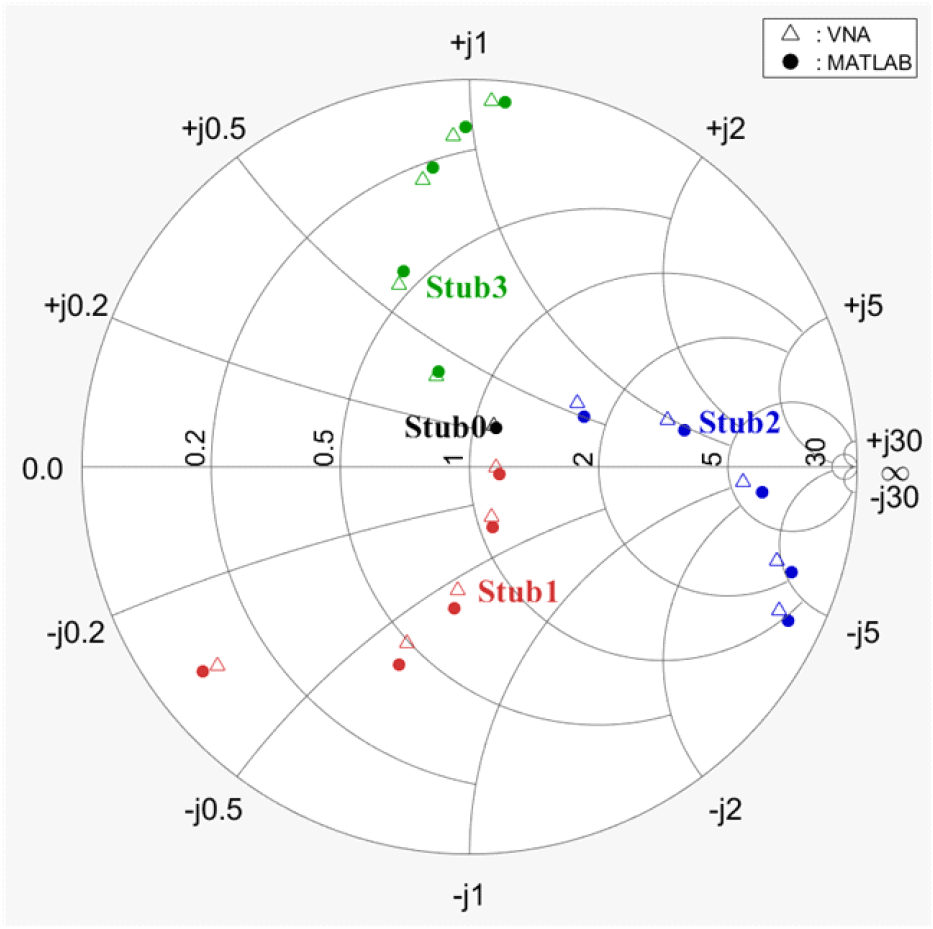
VNA와 MATLAB 측정값의 오차를 줄이는 방법으로는, 소프트웨어적으로 error term을 계산할 시 실제 반사계수 값인 S11A값을 이상적이게 가정하지 않고 open, short, load에 대한 정보를 넣어 총 6개의 방정식을 풀어 error term을 계산한다면 오차가 줄어들 것으로 판단된다. 또한, 하드웨어적으로는 ADC의 전압 해상도를 높이거나 믹서의 출력을 높이면 오차가 줄 것이라 판단된다.
고출력 RF 소스를 이용한 반사계수 측정 시스템에서 프로그램을 이용한 실시간 측정으로 3-stub 튜너를 검증해보았다. 그림 6은 튜너의 각 Stub만 돌려가며 실시간으로 프로그램에서 수집한 반사계수 측정값을 smith chart에 기록한 것이다. 튜너의 입력 포트에서 가까운 Stub부터 하나씩 튜닝하였으며 각각 Stub1, Stub2, Stub3으로 표시했다. Stub들이 끝까지 들어갈 때, 즉 마지막 데이터의 S11 값을 비교해보면, 각각 다음과 같다. Stub1는 0.915∠−141.5, Stub2는 0.921∠−25.4, Stub3는 0.942∠84.5로 각각 Smith chart 상에서 226도, 233도, 239도 차이를 보인다. 따라서 각 Stub가 Smith chart 상에서 대략 λg/3의 위상 차이를 보임을 고출력 동작시스템에서 증명할 수 있었다.
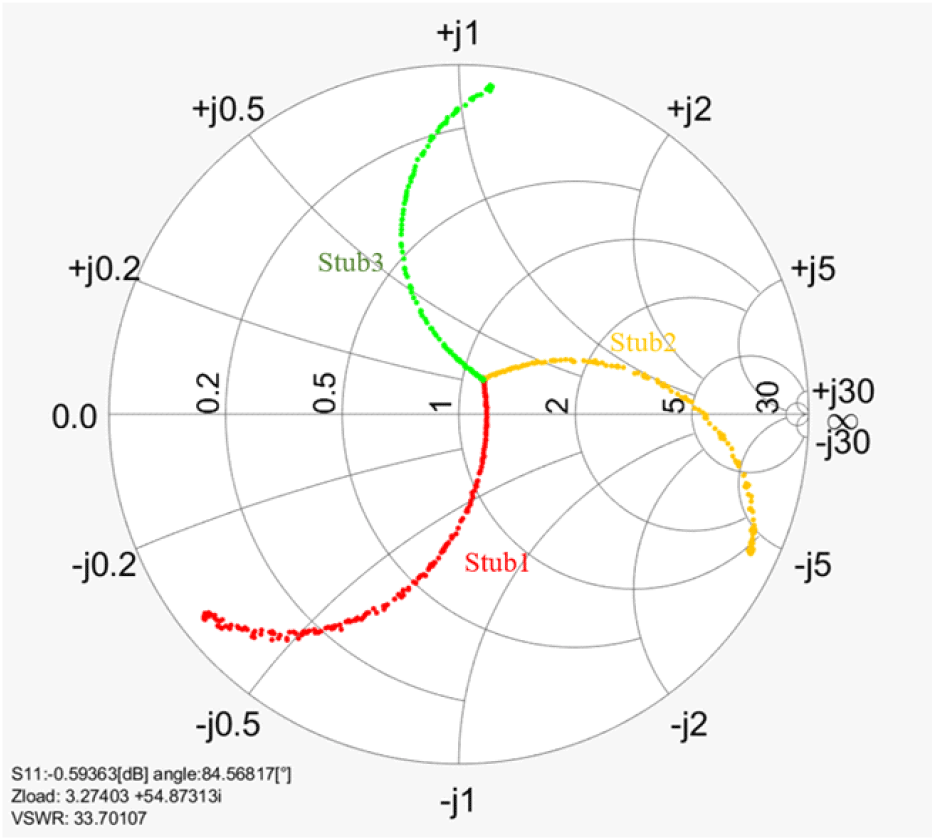
본 논문에서 제안된 시스템은 다음의 기대효과를 제시한다. 고출력 동작 환경에서 특정 RF 소자나 회로의 특성을 측정할 시에 저주파 대역에서만 측정 가능하다는 한계점이 존재했지만, 본 논문에서 제시된 시스템 기반으로 고주파 대역에서도 소자의 특성 측정이 가능하다. 또한, VNA와 같이 고가의 장비를 사용하지 않고 본 논문에서 제시된 이론을 바탕으로 ADC와 MATLAB만으로 시스템을 구현할 수 있다는 장점이 있다.
Ⅴ. 결 론
본 논문에서는 ADS 시뮬레이션을 통해 3개의 error term을 계산하여 이론적으로 시스템을 검증하고, 방향 특성이 좋지 않아도 회로가 잘 동작함을 증명하였다. 위의 검증을 바탕으로 도파관 시스템을 구성하고 2.45 GHz SSPA를 이용하여 고출력 RF 소스를 이용한 반사계수 측정 시스템을 구현할 수 있었다. 또한, 시스템에서 ADC로 수신한 입사파와 반사파를 디지털 데이터로 받아와 실시간으로 반사계수로 변환할 수 있는 프로그램을 설계하였다. 설계한 시스템을 검증하기 위해서 도파관 3-stub 튜너를 DUT에 연결하여 프로그램으로 계산한 반사계수 값을 VNA에서 측정한 값과 실시간으로 비교 분석하였다. 프로그램과 VNA 간 오차가 존재하지만, 이는 사용한 믹서 특성과 ADC의 전압 해상도, 노이즈 문제 때문에 발생된다고 추정된다. 하지만 이는 고출력 동작 환경에서 충분히 수용한 오차로 판단되어 시스템이 잘 구현되었음을 확인할 수 있었다.