The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(1):59-66

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.1.59

논문/REGULAR PAPER

초수평선 레이다를 위한 고해상도 거리분해능 기술에 관한 연구

김형수

, 손성환^*

, 문현욱^*

, 이기원^*

, 최준혁^*

, 김은희^**^,^†

Study on the High Range Resolution for Over-the-Horizon Radar

Hyoung-soo Kim

, Sunghwan Sohn^*

, Hyunwook Moon^*

, Kiwon Lee^*

, Jun Hyeok Choi^*

, Eunhee Kim^**^,^†

한국공학대학교 전자공학과

^*LIG넥스원(주)

^**세종대학교 국방시스템공학과

Department of Electronic Engineering, Tech University of Korea

^*LIG Nex1 Co., Ltd.

^**Department of Defense System Engineering, Sejong University

^†Corresponding Author: Eusuk Shim (e-mail: eunheekim@sejong.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 18, 2023; Revised: Aug 31, 2023; Accepted: Nov 13, 2023

Published Online: Jan 31, 2024

요 약

초수평선 레이다(over-the-horizon radar, OTH radar)는 지구 곡률을 따라 레이다 신호를 지평선 너머로 전파시켜 멀리 떨어진 다양한 대상을 탐지하고 추적하는 기술이다. 이 기술은 이웃 국가로부터의 잠재적인 위협에 대응하기 위해 중요한 역할을 하지만, 아직까지 국내에서는 구현되어 실전 사용이 되지 못하고 있다. 초수평선 레이다 시스템은 멀리 떨어진 대상을 감지하기 위해 단파 주파수(3~30 MHz)를 사용하는데, 이로 인해 대역폭이 제한되어 결과적으로 거리 해상도가 낮아지는 단점이 있다. 이러한 한계를 극복하기 위해 본 연구는 좁은 대역폭의 전송 펄스 파형의 거리 해상도를 향상시키기 위해 하이브리드 최소자승법 수신 필터를 구성하는 데 초점을 맞추었다. 이 필터는 기존의 정합 필터와 최소자승법을 결합하여 높은 해상도를 유지하면서도 노이즈를 효과적으로 제어한다. 마지막으로, 시뮬레이션 결과들로부터, 이 하이브리드 최소자승법의 성능을 검증하였다.

Abstract

Over-the-horizon (OTH) radar is a technology that propagates radar signals beyond the Earth's curvature along the horizon to detect and track a wide range of distant targets. This technology is crucial in addressing potential threats from neighboring countries; however, it has not been implemented domestically for practical use. The OTH radar system utilizes high frequencies (3~30 MHz) to detect distant targets, resulting in a limited bandwidth and, consequently, reduced range resolution. To overcome these limitations, this study focused on enhancing the range resolution of narrow-bandwidth transmission pulse waveforms by constructing a hybrid least-squares reception filter. This filter combines the outputs processed using matched filters and the least-squares method to effectively maintain a high resolution while controlling noise. Finally, simulation results confirmed the improvement in the range resolution of the OTH radar through the application of this hybrid reception filter.

Keywords: OTH Radar; Waveform; Range Resolution

Ⅰ. 서 론

3~30 MHz에서 운용하는 단파 대역(HF) 레이다는 해상 상태 모니터링 및 선박 탐지를 위한 중요한 해상 감시 센서이다^[1],[2]. 일반적으로 레이다에 사용되는 마이크로웨이브(microwave)는 직진성을 가지고 있어, 지구 곡률로 인한 수평선을 넘어서는 탐지가 불가능한 블라인드(blind)영역이 발생한다. 그러나 HF대역의 전파는 전리층을 통한 하늘파(skywave)나 표면파(surface wave) 방식으로 수평선 너머에 대한 탐지가 가능하여, 배타적 경제수역(EEZ), 즉 200해리(NM) 구역까지도 감시할 수 있는 유일한 센서로 역할하고 있다^[3],[4].

그러나, HF 대역은 주파수가 낮고, 스펙트럼 내 사용자가 많아 일반적으로 사용 가능한 순시 대역폭이 40KHz 이하이며, 이로 인해 거리 해상도가 좋지 못하다. 또, 파장이 수백미터로 매우 길기 때문에 큰 안테나를 써도 각도 해상도가 낮아서 장거리에서 교차 거리(cross range)해상도 역시 좋지 못하다. 최근 각도 해상도 향상을 위해 다중 입출력(MIMO)방식을 이용한 가상 안테나와 위상코드 변조를 적용하는 펄스 도플러 방식의 레이다에 대한 연구가 활발해지고 있다^[5],[6].

본 연구에서는 펄스 방식을 사용하는 초수평선 레이다에서 낮은 거리 해상도 문제를 해결하기 위한 방법을 제안하고자 한다. 펄스 레이다에서 거리 해상도를 향상시키기 위한 방법으로 최소자승법(least squares estimator), 적응 펄스 압축법(adaptive pulse compression), 되풀이 MMSE 방법(reiterative MMSE)^[7]~[10] 등이 제안되어 왔다. 최소자승법은 수식적으로 간단하고 빠르게 작동하는 방법이나, 레이다 수신모델에 적용 시, ill-conditioned 특성으로 인해 성능이 저하되므로, 티호노프 정칙화(Tikhonov regularization)를 통해 이 문제를 해결하는 방법이 추가로 연구되었다^[11],[12]. 또한, 최근 인공신경망의 deep learning을 이용해 해상도를 높이려는 연구도 한편에서 시도되고 있으며^[13],[14], FMCW 레이다 영역에서도 MUSIC 알고리즘을 이용한 고해상도 거리-도플러 분해능에 관한 여러 논문^[15],[16]들이 발표되어 왔다.

본 연구에서는 다중 수신 레이다들을 기반으로, 거리-각도 정보를 동시에 고려하면서 좁은 대역폭환경 하의 정합필터의 낮은 타겟 분해능 문제점 해결과 기존의 최소자승추정법의 노이즈에 민감한 문제를 동시에 해결하는 효과적 방법을 제안하고자 한다.

Ⅱ장에서는 거리-각도 정보를 구하기 위한 SIMO(single input multiple output) 레이다 수신모델을 소개한 후, Ⅲ장에서는 소개한 수신모델을 이용한 거리-각도 정보 추출하기 위한 기본알고리즘들 소개와 함께 하이브리드 최소자승법에 대해 정의한다. Ⅳ장에서는 제안한 알고리즘을 이용한 시뮬레이션 결과를 보여주고, Ⅴ에서 결론을 정리한다.

Ⅱ. 시스템 모델

SIMO 레이다 시스템 기반으로 거리-각도 정보를 표기하기 위해, M개의 펄스 반복 주기(PRI, pulse repetition interval)들과 N개의 수신 레이다들을 고려하면 식 (1)과 같은 레이다 수신 모델을 정의할 수 있다^[17]~[19].

y t, m, n = c w t − τ exp j 2 π f d ¯ m × exp j 2 π f a ¯ n + n n o i s e t

(1)

식 (1)에서 w(t)는 송신 레이다파형 함수이고, c는 반사계수, τ는 타겟의 위치에 따른 시간 지연값이며, $f s ¯$ 는 정규화된 공간 주파수(spatial frequency)이다. 수신레이다들 간의 거리는 송신레이다 신호의 반파장(λ/2)만큼 떨어져 있으므로, $f s ¯$ =입력각도/180의 값이 된다. $f d ¯$ 는 정규화된 도플러 주파수로, 시간 지연값 τ의 함수로 나타내면 $f d ¯ τ = f c ⋅ 2 v r P R I / v c = 2 τ / λ$ 이다. 앞의 식에서 f_c는 레이다송신 반송파 주파수, v_r은 타겟의 상대속도, PRI는 펄스 반복 주기, v_c는 광속을 의미한다. 다시 식 (1)에서 m은 펄스 인덱스로 1~M 값을 갖고, n은 수신 레이다 인덱스로 1~N 값을 갖는다.

우선, M개의 펄스 반복 주기 동안에 수신된 수신신호 내의 타겟에 의해 반사된 펄스 신호 성분을 강화하기 위해, M개의 coherent 한 펄스들은 더하면서 크기를 더욱 크게 만들고, noncoherent한 특정을 갖는 노이즈들은 더하면서 상쇄되어 작아지도록 식 (2)를 취한다.

y ¯ t, n = ∑ m = 1 M c w t − τ exp j 2 π f d ¯ m × exp j 2 π f s ¯ n + n n o i s e t

(2)

식 (2)에서 $f d ¯$ 는 함선이나 상대적으로 느린 타겟의 경우, 거의 “0”에 가까운 값으로 수 개의 펄스들을 더할 때, 펄스들의 변화가 거의 없으므로, coherent 가정이 성립한다. 이렇게 처리된 레이다 수신모델을 바탕으로, 이산수신신호 모델을 식 (3)과 같이 다시 쓸 수 있다.

Y = c W x a + N n o i s e

(3)

식 (3)에서 상수 c는 반사계수이고, x는 타겟 위치정보를 담고 있는 L×1 파형 타겟 임펄스 벡터이며, N_noise는 L×N 가우시안 노이즈 행렬이다. L은 한 개의 반복펄스주기를 샘플링한 샘플 개수이다. a는 1×N 공간조향벡터로 a=[a(0) a(1) a(2) … a(N−1)]이고, 이 벡터에서 $a n = e j 2 π f s ¯ n$ 이며 타겟 각도 정보를 담고 있다. W는 L×L 레이다 파형 행렬로 식 (4)와 같다.

W = w 0 000 ⋯ ⋯ 0 w 1 w 0 00 ⋯ ⋯ 0 w 2 w 1 w 0 0 ⋯ ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋯ ⋯ 0 w N − 1 w N − 2 ⋯ w 0 0 ⋯ 0 0 w N − 1 w N − 2 ⋯ w 0 ⋯ 0 ⋮ ⋮ ⋱ ⋱ ⋱ ⋱ 0 0 ⋯ 0 w N − 1 ⋯ w 1 w 0

(4)

Ⅲ. 거리-각도 그래프와 고해상도 분해능

정합필터에 의한 거리-각도 그래프를 표시하기 위해, Y의 행 단위로 FFT(fast Fourier transform)를 취하고, W의 켤레전치(Hermitian)를 한 W^H를 Y의 왼쪽에 곱하여 식 (5)와 같은 결과를 갖는다.

X M F = W H Y F F F T

(5)

식 (5)에서 F_FFT는 FFT를 수행하는 행렬이며, X_MF는 정합필터에 의한 거리-각도 그래프를 담고 있는 행렬이다. 정합필터는 SNR을 최대화하는 필터로 디자인한 것이기에 수신신호에서 노이즈를 효과적으로 제거할 수 있으나, 노이즈 제거 시 수행되는 필터링에 의해 타겟 위치 정보를 담은 펄스폭을 더욱 확장하는 문제점을 가지고 있다. 이에 따라 가까운 거리에 있는 다중 타겟들이 겹치게 되어 타겟 거리해상도를 떨어뜨리는 요인이 된다.

정합필터의 거리 해상도 문제에 대응하기 위해, 정합필터링과 다른 접근 방식으로, 수신신호로부터 타겟의 위치 정보를 담은 x를 추출해야 한다. 이 문제는 본질적으로 수신신호로부터 파형 타겟 임펄스 벡터 x를 추출하는 역방향문제(inverse problem)로 해석할 수 있으며, 이를 의사 역행렬(pseudo inverse)방식으로 해결함으로써 파형 타겟 임펄스 벡터 x의 원형에 더 가까운 결과를 얻을 수 있게 된다. 이 결과, 타겟 위치를 담은 임펄스 파형은 폭이 극도로 좁기에 높은 거리해상도를 얻을 수 있다. 이는 결국 참고문헌 [6]의 최소자승법과 같은 결과로 귀결된다. 다른 한편, 레이다파형에 기반을 둔 의사역행렬 문제는 ill-conditioned 문제의 특징을 가지므로, 다음과 같이 티호노프 정칙화에 기반을 둔 수정된 최소자승법(modified least-square method) 방법으로 문제를 해결한다^[10].

X M L S = W H W + α I − 1 Y F F F T

(6)

식 (6)의 α는 ill-conditioned 문제를 제거하기 위한 상수다. 최소자승법의 기본 작동 원리는 다음과 같이 설명될 수 있다. 여러 개의 타겟이 매우 근접한 위치에 있는 경우, 수신레이다 신호에는 이들 타겟들로부터 반사되어 돌아온 여러 개의 펄스들이 겹쳐 수신된다. 이와 같이 겹쳐 수신된 여러 펄스들을 분석하여 구분/분해하기 위해서, 수신레이다는 기존 정합필터에서 보다 높은 오버 샘플링 주파수로 샘플들을 취한 후 처리해야만 한다. 이들 겹쳐진 수신신호들은 불연속적인 경계파형을 형성하고, 수정된 최소자승법은 불연속적인 경계면 정보를 기반으로 다중타겟의 위치정보를 임펄스 신호로 변화시키는 필터로 작동된다. 이는 일종의 고주파 필터와 비슷하게 작동되기에 노이즈가 심한 수신신호에 대해서는 타겟 위치 정보들에 의해 만들어진 임펄스들과 노이즈에 의해 만들어진 임펄스들이 뒤섞여, 그림 1처럼 원하는 타겟 정보를 구분하기 힘들게 된다. 이 노이즈 문제점에 대한 해결책으로, 정합필터와 수정 최소자승법의 장점을 융합한 하이브리드 최소자승법을 식 (7)과 같이 정의한다. 이는 노이즈에 민감한 기존 최소자승법 필터의 문제점을 해결하고, 타겟 임펄스 정보의 메인로브(main-lobe) 옆 사이드 로브(side-lobe)를 추가적으로 더욱 감쇠시킬 수 있게 된다.

X H L S = β W H Y F F F T ∘ W H W + α I − 1 Y F F F T

(7)

그림 1. | Fig. 1. 노이즈 환경에 두 타겟 정보가 숨겨져 구분되지 못하는 수정 최소자승법의 결과 | Modified least squares method results in which two target information cannot be distinguished under a noisy environment.

Download Original Figure

식 (7)에서 “∘”은 두 행렬의 원소단위의 연산을 정의하는 Hadamard product를 의미한다.

Ⅳ. 시뮬레이션 결과

시뮬레이션에 사용된 파라미터들은 표 1과 같다. 공간주파수에 의한 각도 정보를 위해 FFT출력은 제로패딩을 통해 512 샘플 결과가 나오도록 설정했다. 송신 레이다파형의 사각펄스폭은 송신 레이다 파형의 대역폭인 5kHz에 맞춰, 약 200 μs 폭으로 설정했으며, 펄스 반복 주파수 (PRF, pulse repetition frequency)는 300 Hz이므로, 최대 유효 탐지거리(maximum unambiguous range)는 500 km가 된다. 파형 타겟 임펄스 벡터 x에는 표 1과 같이 첫 번째 타겟 (400 km, 30°)과 두 번째 타겟(420 km, 30°)을 넣어 실험했다.

표 1. | Table 1. 시뮬레이션 운용 지표 | Parameters of simulation.

Number of radars	6
Carrier frequency	5 MHz
Bandwidth	5 kHz
Pulse repetition frequency	300 Hz
FFT size	512 samples
Reflective coefficient in (2), c	0.2
Complex random noise power	1
Target information	(400 km, 30°) (420 km, 30°)
Sampling frequency	150 kHz

Download Excel Table

기본적으로 신호의 파워에 비해 노이즈 파워가 크므로, 식 (2)에서 정의한 수신신호 사전처리로 5개의 연속적 펄스 반복 주기 신호들을 합산하여, 1차적 노이즈 제거를 수행했다. 타겟들은 함선을 기준으로 각기 25노트와 22노트로 일정하게 움직이는 것으로 설정했기에, 5개의 연속적 펄스 반복 주기 동안 타겟들의 위치 변화는 거의 없다. 이러한 결과로 인하여, 펄스 반복 주기 간의 도플러 주파수 변화에 따른 영향이 최소화되며, 일관된 타겟 특성이 유지된다. 이에 따라 타겟 펄스 신호 왜곡이 거의 없이 합산되어 거리정보의 왜곡이 최소화되며, 원하는 타겟 신호를 효과적으로 강화할 수 있게 된다. 본 논문에서 제안하는 하이브리드 최소자승법의 전체 블록 다이어그램은 그림 2와 같다.

그림 2. | Fig. 2. 하이브리드 최소자승법의 블록다이어그램 | Hybrid least squares method block diagram.

Download Original Figure

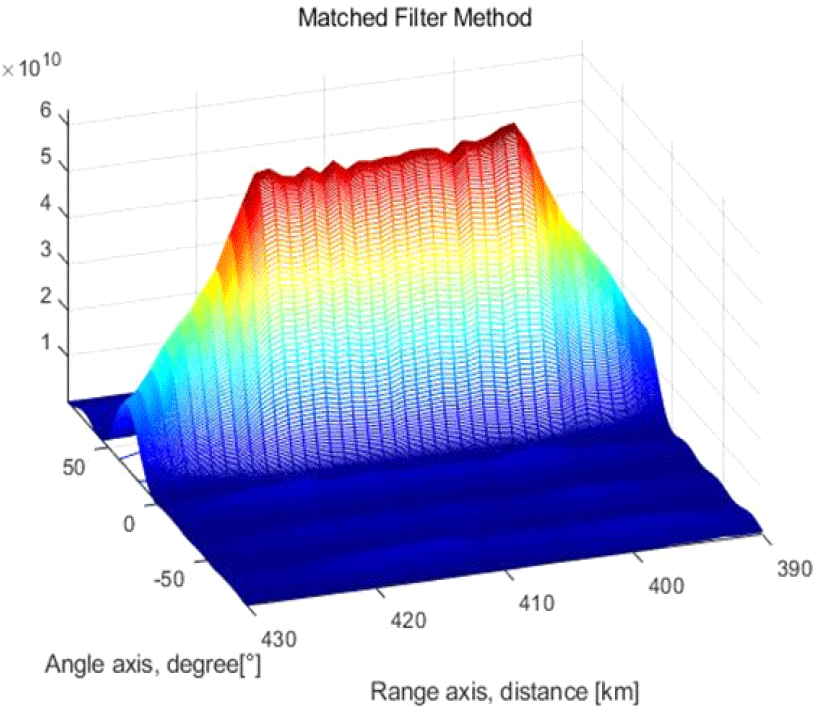
첫 번째, 정합필터를 사용한 거리-각도 그래프는 그림 3과 같다. 정합필터 디자인 특성상 가우시안 노이즈가 거의 사라진 것을 볼 수 있으나, 첫 번째 타겟(400 km, 30°)과 두 번째 타겟 (420 km, 30°)이 구분되지 못하고 한꺼번에 하나의 펄스에 뭉개져 표시된 것을 볼 수 있다.

그림 3. | Fig. 3. 정합필터 결과 | Matched filter result.

Download Original Figure

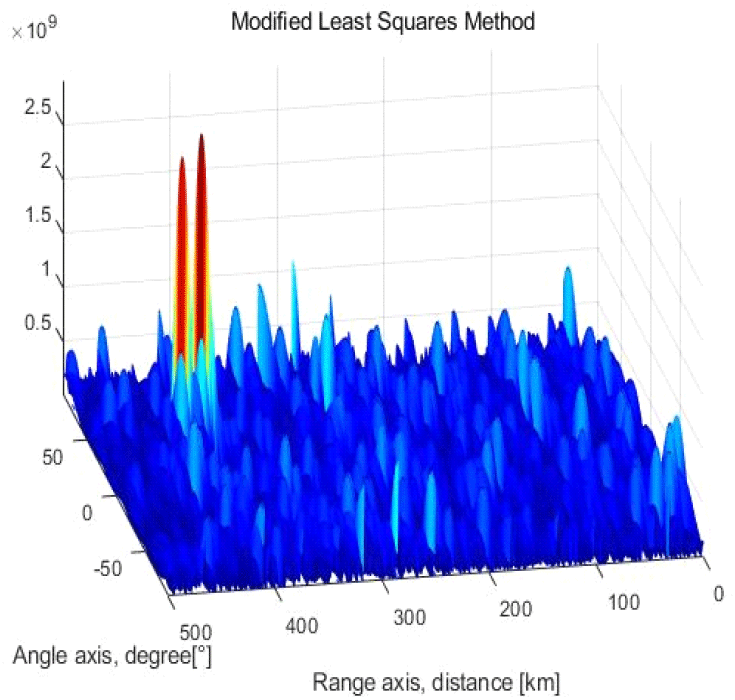
그림 4는 최소자승법에 의한 거리-각도 그래프 결과이다. 여기서는 정합필터 결과보다 노이즈 파워가 크지만, 두 개의 타겟이 400 km, 420 km에서 명확히 구분된다.

그림 4. | Fig. 4. 수정된 최소자승법 출력 | Least squares method result.

Download Original Figure

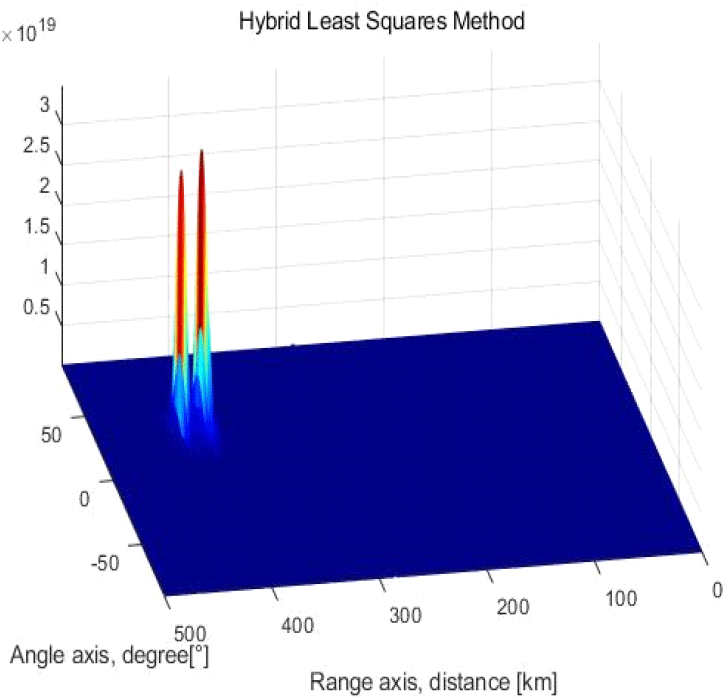
그림 5는 하이브리드 최소자승법의 출력을 보여준다.하이브리드 최소자승법의 경우, 정합필터의 노이즈제거 특성과 최소자승법의 높은 거리분해능의 장점들을 동시에 갖는 것을 확인할 수 있다.

그림 5. | Fig. 5. 하이브리드 최소자승법 출력 | Hybrid least squares method result.

Download Original Figure

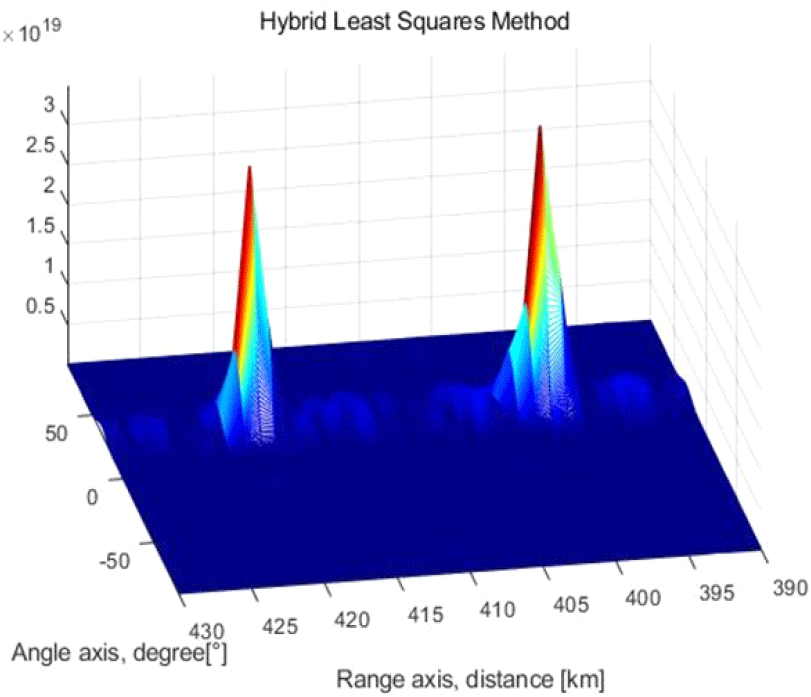
보다 면밀한 거리해상도 성능 비교를 위해 정합필터와 하이브리드 최소자승법의 결과인 그림 3 및 그림 5의 거리축 390~430 km부분을 확대 비교하면 그림 6 및 그림 7과 같다. 그림 6의 정합필터 결과에서는 두 타겟이 합쳐져 몇 개의 타겟이 어디에 각기 위치해 있는지 알 수가 없는 상태이나, 하이브리드 최소자승법의 결과인 그림 7의 경우 노이즈가 거의 제거됨과 동시에 매우 높은 거리 해상도를 가지기에 400 km와 420 km에 존재하는 타겟을 뚜렷하게 구분할 수 있다.

그림 6. | Fig. 6. 두 타겟 부근을 확대한 정합필터 출력 | Expanded matched filter output near the two targets.

Download Original Figure

그림 7. | Fig. 7. 두 타겟 부근을 확대한 하이브리드 최소자승법 출력 | Expanded hybrid least squares method output near the two targets.

Download Original Figure

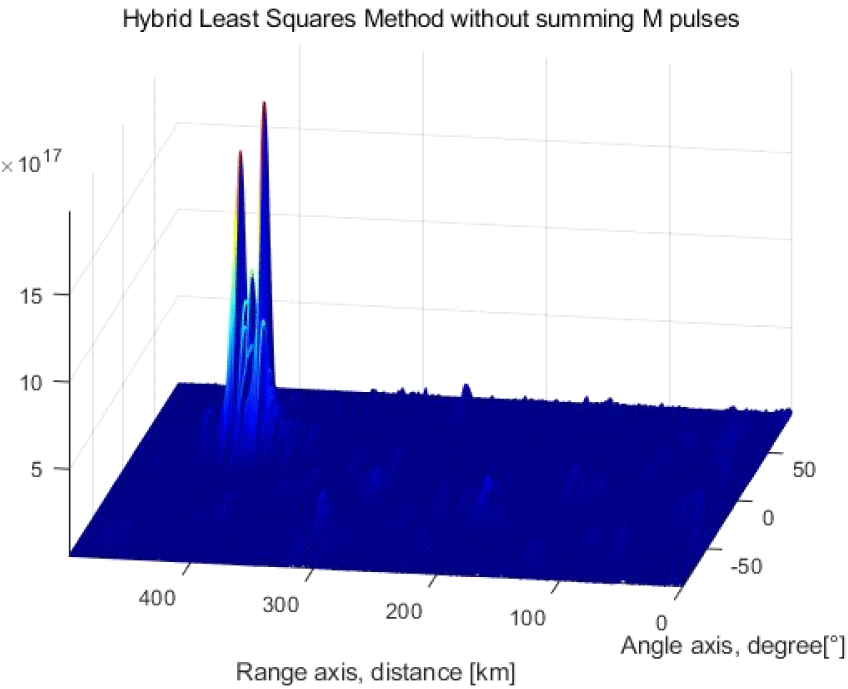
다른 한편 SNR을 높이기 위한 M개 펄스반복주기들의 합산과정을 거치지 않은 경우, 본 시뮬레이션에서 정의한 수신 신호의 기본 SNR이 낮은 상태이기 때문에 그림 1의 수정 최소자승법의 경우 타겟에 대한 정보를 전혀 찾지 못한다. 하지만 같은 신호에 대해 수신기를 하이브리드 최소자승법으로 바꿔 적용하는 경우 그림 8과 같이 타겟 탐지가 가능하고 어느 정도 2개의 타겟이 구분되고 있는 것을 확인 할 수 있다.

그림 8. | Fig. 8. M 펄스반복주기 합산 없이 수행한 하이브리드 최소자승법 출력 | Hybrid least squares method performed without summing up M pulse repetition intervals.

Download Original Figure

본 연구에서 수행한 시뮬레이션에서는 송신 레이다 파형으로써, 하나의 단순 사각펄스를 이용하여 시뮬레이션을 했으나, 이 사각 펄스를 칩 단위로 조합하여 Barker code와 같은 송신 레이다 파형을 보낼 경우, 펄스 압축 특성으로 인해 보다 높은 SNR을 유지하기에 더욱 좋은 결과를 기대할 수 있다.

Ⅴ. 결 론

본 연구에서는 대역폭이 제한된 전송 펄스 파형을 사용하는 초수평선 레이다와 같은 상황에서 어떻게 높은 거리 해상도를 수신단의 프로세스를 통해 개선할 수 있는지 방법을 살펴보았다. 레이다 수신신호의 노이즈 수준에 따라 여러 펄스 반복 주기 단위로 합산하여 노이즈를 감소시키고, illconditioned 상태를 개선하는 최소자승법을 이용하여 처리된 출력과 노이즈에 강한 정합필터 결과를 조합하여 하이브리드 수신 필터를 구성했다. 시뮬레이션 결과를 통해, 이러한 접근 방식이 높은 거리해상도와 효과적인 노이즈 감소 효과를 동시에 달성할 수 있음을 확인하였다.

제안한 하이브리드 수신 필터를 통해 구분 가능한 최소 거리해상도는 보다 높은 수신신호 샘플링과 함께 수신신호 SNR을 높일 경우 향상시킬 수 있다. 이 거리 해상도의 정량적/수치적 한계치는 하이브리드 필터링으로 구한 거리-각도 데이터를 기반으로, 추가적인 목적 파라미터별 추정치를 수치적으로 계산하거나 혹은 그래프 단위로 여러 실험을 통해 상황별 case study 수행이 필요하다. 향후 이를 위한 추가적 연구와 MIMO 레이다 구성을 통해 얻을 수 있는 추가적인 거리해상도 향상에 관한 연구를 수행할 예정이다.

Acknowledgements

이 연구는 LIG Nex1 산학 협력과제 지원으로 연구되었음.

References

[1].

W. Sun, M. Ji, W. Huang, Y. Ji, and Y. Dai, “Vessel tracking using bistatic compact HFSWR,” Remote Sensing vol. 12, no. 8, p. 1266, 2020.

[2].

T. Ponsford, J. Wang, “A review of high frequency surface wave radar for detection and tracking of ships,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 18. no. 3, pp. 409-428, 2010.

[3].

X. Ji, J. Li, and Q. Yang, “Annual characteristic analysis of ionosphere reflection from middle-latitude HF over-the-horizon radar in the northern hemisphere,” IEEE Transactions on Geoscience and Remote Sensing, vol. 61, pp. 1-17, 2023.

[4].

M. I. Skolnik, Radar Handbook, 3rd ed. New York, NY, McGraw Hill, 2008.

[5].

G. J. Frazer, Y. I. Abramovich, B. A. Johnson, and F. C. Robey, “Recent results in MIMO over-the-horizon radar,” in 2008 IEEE Radar Conference, Rome, 2008, pp. 1-6.

[6].

R. J. Riddolls, “A Canadian perspective on high frequency over-the-horizon radar,” Defence R&D Canada–Ottawa, DRDC Ottawa TM 2006-285, Dec. 2006.

[7].

S. D. Blunt, K. Gerlach, “Adaptive pulse compression via MMSE estimation,” IEEE Transactions on Aerospace and Electronic Systems, vol. 42, no. 2, pp. 572-584, Apr. 2006.

[8].

S. M. H. Song, W. M. Kim, D. Park, and Y. S. Kim, “Estimation theoretic approach for radar pulse compression processing and its optimal codes,” Electronic Letters, vol. 36, no. 3, pp. 250-252, Feb. 2000.

[9].

S. D. Blunt, K. Gerlach, and T. Higgins, “Aspects of radar range super-resolution,” in IEEE Radar Conference, Waltham, MA, 2007, pp. 683-687.

[10].

B. Zrnic, A. Zejak, A. Petrovic, and I. Simic, “Range sidelobe suppression for pulse compression radars utilizing modified RLS algorithm,” in IEEE 5th International Symposium on Spread Spectrum Techniques and Applications, Sun City, Sep. 1998, pp. 1008-1011.

[11].

A. N. Tikhonov, “Solution of incorrectly formulated problems and the regularization method,” Soviet Mathematics Doklady, vol. 4, no. 6, pp. 1035-1038, 1963.

[12].

H. W. Engl, M. Hanke, and A. Neubauer, Regularization of Inverse Problems, Dordrecht, Kluwer Academic Publishers, 1996.

[13].

G. Andrew, J. C. Hardin, “Radar super resolution using a deep convolutional neural network,” Journal of Atmospheric and Oceanic Technology, vol. 37, no. 12, pp. 2197-2207, 2020.

[14].

C. Schuessler, M. Hoffmann, and M. Vossiek, “Super-resolution radar imaging with sparse arrays using a deep neural network trained with enhanced virtual data,” IEEE Journal of Microwaves, vol. 3, no. 3, pp. 980-993, Jul. 2023.

[15].

Y. Gürcan, A. Yarovoy, “Super-resolution algorithm for joint range-azimuth-Doppler estimation in automotive radars,” in 2017 European Radar Conference(EURAD), Nuremberg, Oct. 2017, pp. 73-76.

[16].

S. Xu, J. Wang, and A. Yarovoy, “Super resolution DOA for FMCW automotive radar imaging,” in 2018 IEEE Conference on Antenna Measurements & Applications(CAMA), 2018, pp. 1-4.

[17].

C. Y. Chen, P. P. Vaidyanathan, “MIMO radar ambiguity properties and optimization using frequency-hopping waveforms,” IEEE Transactions on Signal Processing, vol. 56, no. 12, pp. 5926-5936, Dec. 2008.

[18].

S. Badrinath, A. Srinivas, and V. U. Reddy, “Low-complexity design of frequency-hopping codes for MIMO radar for arbitrary Doppler,” EURASIP Journal on Advances in Signal Processing, vol. 2010, p. 319065, Feb. 2010.

[19].

J. Ward, “Space-time adaptive processing for airborne radar,” Lexington MA, Lincoln Laboratory, TR-1015, 1994.