The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(9):666-674

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.9.666

논문/REGULAR PAPERS

Reaction 이론을 이용한 통합 마스트 배열 안테나 간 간섭도 계산

김우태^†

, 고정호

, 고일석^*

, 배기웅^**

Application of the Reaction Theorem to Calculate the Coupling between Array Antennas on an Integrated Mast

Wootae Kim^†

, Jeong-Ho Ko

, Il-Suek Koh^*

, Ki-Woong Bae^**

㈜애니캐스팅 소프트웨어

^*인하대학교 전자공학과

^**국방과학연구소 함정전투체계단

AnyCasting Software Co., Ltd.

^*Department of Electronic Engineering, Inha University

^**Maritime Technology Research Institute, Agency for Defense Development

^†Corresponding Author: Wootae Kim (e-mail: wootae.kim@anycasting.com)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 16, 2023; Revised: Sep 09, 2023; Accepted: Sep 21, 2023

Published Online: Sep 30, 2023

요 약

본 논문에서는 안테나 간 간섭도 계산을 빠르게 수행하기 위해 reaction theorem을 간섭도 계산에 적용하였다. 기존 안테나 간섭도 계산 방법은 동일한 안테나를 대상으로 거리나 위치만 변경하여도 full wave 해석을 매번 수행해야 하므로 많은 해석 시간이 필요했다. Reaction theorem을 이용한 안테나 간 간섭도 계산 시 개별 안테나 해석은 full wave 해석 결과를 활용하고, 안테나 배치와 플랫폼 효과를 포함한 해석은 reaction을 이용하므로 빠르게 계산을 할 수 있다. 안테나 간섭도 계산에 reaction을 적용하기 위해 이론을 정리하고, reaction의 유용성을 검증하기 위해 blade 안테나와 wire 다이폴 안테나를 이용해 full wave 해석과 비교하였다. 이때 도체 평판의 플랫폼 효과를 반영하기 위해 image theory를 적용하였다. 마지막으로 배열 안테나를 수직 미소 다이폴로 구성하고 통합마스트 형상에서 이웃한 면에 두 개의 배열 안테나를 배치하여 주 빔 방향에 따른 배열 안테나 간 reaction을 계산하였다.

Abstract

This study applies the reaction theorem to efficiently calculate the interference between antennas. Conventional methods to calculate the interference between antennas required a full-wave analysis when the distance or position between the antennas was changed, increasing the analysis time. By utilizing the reaction theorem for the antenna interference calculations, the individual antennas can be analyzed using the full-wave analysis, and environmental effects, such as antenna placement and platform, can be considered using the reaction theorem. The reaction theorem was applied to formulate the antenna interference problem. The proposed scheme was validated by comparing the results computed utilizing the reaction theorem and those computed by full-wave analysis of the coupling between blade and wire dipole antennas. The effect of the conducting plates was considered by applying the image theory. Finally, the coupling between two array antennas was considered. The array comprised vertical infinitesimal dipoles. Two arrays were placed on the neighboring faces of the integrated mast structure and the reaction between the arrays was calculated as a function of the main beam direction.

Keywords: Coupling beween Antennas; Integrated Mast; Reaction Theorem

Ⅰ. 서 론

현대 해군 함정은 해상에서 대함/대공/대잠/대지 등 복합전 개념의 다중 위협에 대한 작전과 해양통제권 확보 및 해상교통로(CLOS: sea line of communications) 보호와 같은 다양한 임무를 수행하고 있다. 이에 따라 다양한 통신 시스템과 레이다, 전자전 장비뿐만 아니라, 안테나를 사용하고 있는 무장 장비 배치로, 전파 송수신 시스템의 복잡도가 증가하고 있다. 함정 외부 상부구조에 다양한 임무 장비 배치와 함께 안테나 수의 증가는 전자기 간섭(electromagnetic interference: EMI) 문제와 레이다 반사면적(radar cross section: RCS)을 증가시켜 함정의 생존성 감소를 초래한다^[1]. 함정의 전자 통신 장비의 본 임무 수행을 추구하면서, 시스템과 안테나의 증가에 따른 단점을 최소화하기 위해 세계 각국의 해군 함정들은 통합마스트를 개발하여 탑재하였다. 통합마스트는 안테나들이 밀집되어 있어 장비들을 동시에 운영할 경우에 전자파 간섭으로 인한 성능 저하가 발생할 수 있다. 센서 장비들은 기본 운용 주파수 외에도 스퓨리어스 발사(spurioirs emission), 대역 외 발사(out-of-band emission)와 같이 매우 넓은 주파수대역에서 신호를 방출하기 때문에 전 주파수 대역의 해석을 통한 전자파 간섭 분석이 필요하다. 안테나 전자파 간섭도, 결합 분석은 근역장 해석을 요하는 관계로 해석 시간을 줄이기 위해 full-wave 해석 대신 다양한 모델을 적용한 연구가 진행되고 있다^[2]. 통합마스트상의 분석은 대형 플랫폼에 정밀한 형태의 안테나 형상을 포함하여 MoM(method of moments) 같은 full-wave 방법의 적용이 매우 어렵다.

본 논문에서는 통합마스트 위에 배치된 다양한 안테나 간의 간섭도 계산을 빠르게 수행하기 위해 reaction theorem^[3]~[5]을 적용하였다. 안테나 간 간섭도 계산은 안테나의 정확한 해석을 요하기 때문에 full wave 해석을 기본적으로 사용한다. 이때 해석 대상이 동일한 안테나인 경우에도 위치나 플랫폼의 변경이 생길 때마다 안테나를 포함한 전체 해석을 다시 수행해야 한다. Reaction을 이용한 안테나 간섭도 계산은 개별 안테나에 대한 full wave 해석 결과를 변경된 배치나 플랫폼에 의한 안테나 간 간섭도 계산 시 재해석 없이 재활용할 수 있는 장점이 있어서, 해석 시간을 크게 줄일 수 있다. 본론에서는 간섭도 계산에 대한 reaction theorem을 이론을 정리하고, reaction의 유용성을 검증하기 위해 blade 안테나와 wire 다이폴 안테나를 이용해 간섭도 계산 결과를 full wave 해석과 비교 검증한다. 이때 동일 평판 위에 존재하는 안테나 간 간섭도 계산은 도체 평판의 플랫폼 효과를 반영하기 위해 image theory를 적용하고, 거리별, 주파수별 해석을 수행한다. 기존 방법은 안테나 주변의 구조물까지 포함한 full-wave 해석 방법을 사용하고, reaction을 이용하여 안테나간 간섭도 계산을 하였다. 그러나 통합마스트 같은 구조물이 단순한 경우에 계산량이 불필요하게 많아, 통합마스트상의 여러 안테나 간 간섭도 계산에 직접 적용하기에 한계가 존재한다. 그러므로, 평면 위에 놓여있는 안테나 사이 간섭도 계산을 효율적으로 수행할 방법이 필요하다. 본 연구에서는 image theory와 reaction을 결합하는 효율적인 방법론을 제시하고 정확도를 검증한다. 마지막으로 통합마스트 옆면에 위치한 배열 안테나에 대한 reaction은 모서리 회절을 이용해 계산하도록 한다. 수직 미소 다이폴을 기본 소자로 갖는 2차원 배열 안테나를 설계하고, 통합마스트 형상에서 이웃한 면에 두 개의 배열 안테나를 배치하여 주 빔 방향에 따른 배열 안테나 간 reaction을 계산하여 특성을 분석한다.

Ⅱ. 본 론

Reciprocal theorem은 회로, 필드, 그리고 회로와 필드가 같이 존재하는 혼합형에 대해, 세 가지 방식으로 표현된다. 회로에 대한 reciprocal theorem은 다음과 같다^[3].

V 12 I 11 = V 21 I 22

(1)

여기서V₁₂는 회로 포트 2의 전류원 I₂₂에 의해 포트 1에 여기된 전압을 의미하고, V₂₁은 포트 1의 전류원 I₁₁에 의해 여기된 포트 2의 전압을 나타낸다. 필드 형태의 reciprocal theorem은 식 (2)와 같다.

∮ S 1 E 1 × H 2 − E 2 × H 1 ⋅ d S = ∮ S 2 E 2 × H 1 − E 1 × H 2 ⋅ d S

(2)

식 (2)에서 적분은 reaction이라 알려져 있고, 필드와 소스 사이에 식 (3)과 같은 관계를 갖는다.

1, 2 = ∫ V 1 E 2 ⋅ J 1 − H 2 ⋅ M 1 d V = ∮ S 1 E 1 × H 2 − E 2 × H 1 ⋅ n^d S

(3a)

2, 1 = ∫ V 2 E 1 ⋅ J 2 − H 1 ⋅ M 2 d V = ∮ S 2 E 2 × H 1 − E 1 × H 2 ⋅ n^d S

(3b)

여기서 E_i와 H_i는 소스 i에 의해 생성되는 전자기파이다. reciprocal theorem은 <1,2≧<2,1>로 간단히 표현 가능하다. 식 (1) 및 식 (2)를 합하여 회로와 필드의 혼합형 표현식은 식 (4)와 같다.

V 12 I 11 = − 1, 2

(4a)

V 21 I 22 = − 2, 1

(4b)

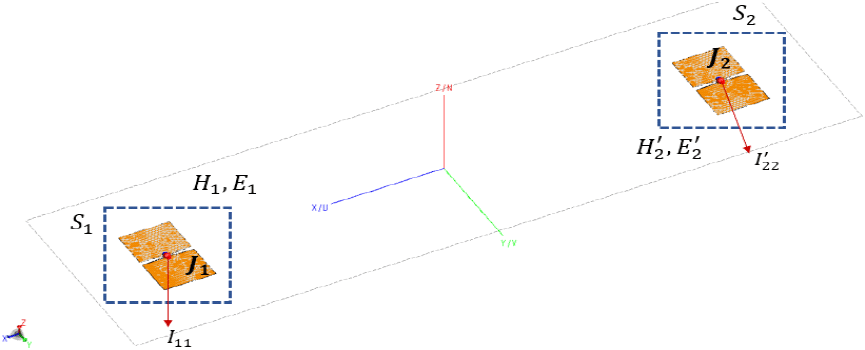
식 (4a) 및 식 (4b)를 이용하여 회로 내의 전압과 전류를 필드 성분으로부터 계산 가능하다. 그림 1은 식 (4a) 및 식 (4b)를 사용하는 경우의 환경을 보여준다. 보다 일반적인 환경에서의 reciprocal theorem은 참고문헌 [3]에 설명되어 있다.

그림 1. | Fig. 1. 안테나 간 reaction을 이용한 간섭도 계산 방법 | Method of calculation of coupling between antennas by using the reaction.

Download Original Figure

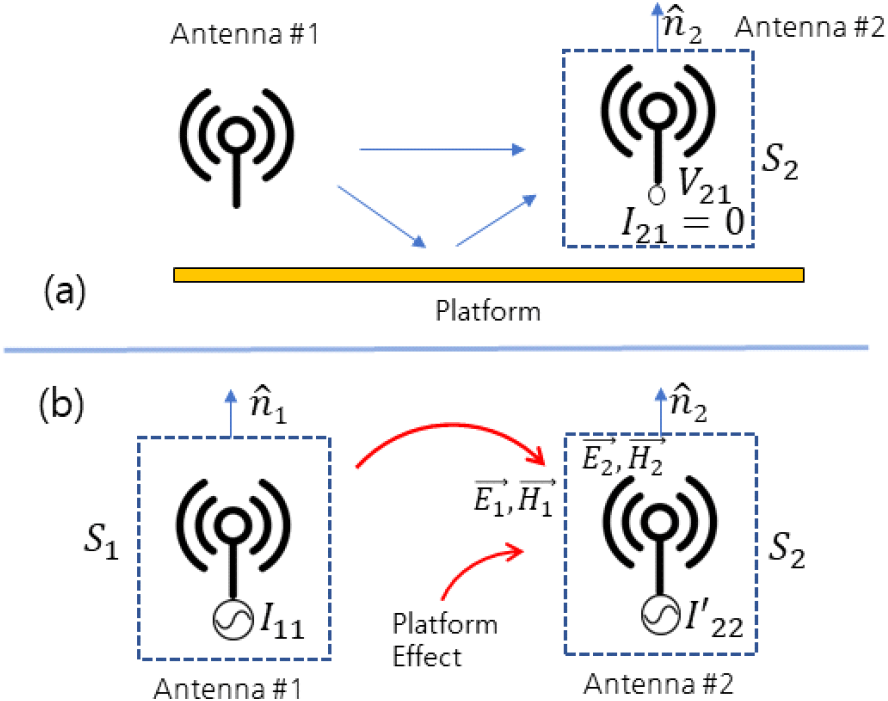
식 (3a) 및 식 (3b)를 계산하기 위해 적분 면 S₁과 S₂를 선택해야 한다. S₁는 안테나 1를, S₂는 안테나 2를 감싸는 임의의 면이 된다. 소스 1에서 발생하는 필드를 S₂면에서 계산하는 경우 안테나 주변 환경을 고려해서 계산하고 또, 소스 2에서 발생하는 필드 또한 주변 환경의 영향을 고려해야 한다. 만약 소스 2에서 발생하는 필드가 소스 1에서 반사하여 주변 환경과 상호작용하는 효과가 매우 작으면, 식 (3a) 및 식 (3b)를 계산 시, 소스 2에 의한 S₂면 위 필드는 소스 1이 없다고, 반대로 소스 1에 의한 필드는 소스 2가 없다고 가정하고 계산할 수 있다. 또, 주변 환경을 고려하는 경우 full-wave 방법 외 ray-tracing, UTD (uniform theory of diffraction) 같은 보다 효율적인 방법을 사용할 수 있다. 이런 가정을 바탕으로 식 (3a) 및 식 (3b)를 상대적으로 간단하게 계산할 수 있고, 그 후 식 (4a) 및 식 (4b)를 이용하여 회로내의 전류 또는 전압을 계산할 수 있다.

그림 1에서 안테나 1과 안테나 2의 상호임피던스는 앞서 기술된 과정을 이용해 식 (5)로 구할 수 있다.

Z 21 = V 21 / I 11 = − 1 I 11 I 22 ′ ∮ S 2 E 2 ′ × H 1 - E 1 × H 2 ′ ⋅ n 2^d S = − 1 I 11 I 22 ′ ∫ V 2 E 1 ⋅ J 2 ′ − H 1 ⋅ M 2 ′ d V

(5)

2-포트 네트워크에서 Z₂₁을 산란 계수 (S₂₁)로 식 (6)과 같이 변환된다^[6].

S 21 = 2 Z 21 Z 0 Z 11 + Z 0 Z 22 + Z 0 − Z 12 Z 21 = 2 Z 21 Z 0 Z 11 + Z 0 Z 22 + Z 0 1 1 − Z 12 Z 21 Z 11 + Z 0 Z 22 + Z 0

(6)

일반적으로 자기 임피던스(self-impedance) Z₁₁, Z₂₂값이 상호 임피던스(mutual impedance) Z₂₁ (=Z₁₂)의 크기에 비해 매우 크므로 |Z₁₁Z₂₂| ≫ |Z₂₁Z₁₂| 가 성립된다. 그러므로 식 (6)의 대괄호 내 식은 1로 근사화할 수 있어, 식 (7)과 같이 S₂₁이 간단히 된다^[5].

S 21 ≃ Z 21 2 Z 0 Z 11 + Z 0 Z 22 + Z 0

(7)

두 안테나 사이의 coupling을 계산 시, 먼저 각 안테나 특성인 자기 임피던스와 방사 필드 계산에 필요한 표면전류는 MoM 같은 full-wave 방법을 이용하여 계산한다. 그 후 이를 이용하여 reaction을 계산하고 식 (5) 및 식 (7)을 이용하여 최종적으로 S₂₁을 예측한다.

Ⅲ. 수치 결과

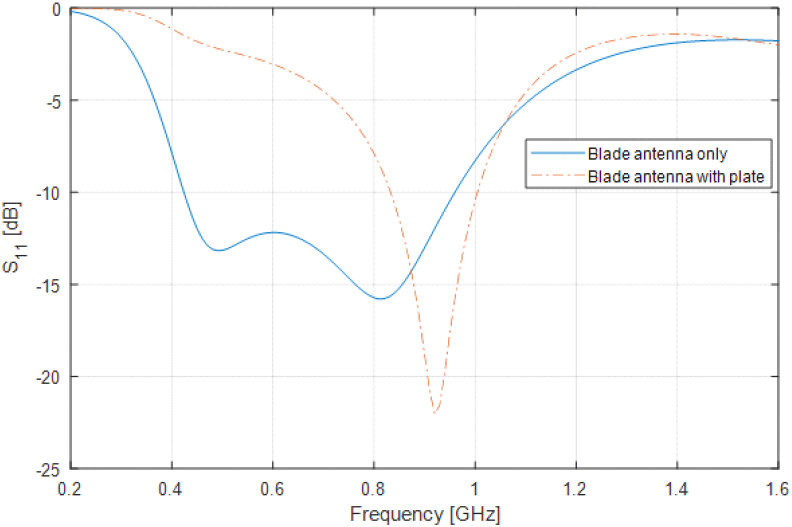
먼저 제안된 방법의 정확도를 검증하였다. 두 안테나가 자유공간에 놓여 있는 경우를 고려하였다. 안테나는 참고문헌 [7]의 광대역 Blade 다이폴 안테나 모델을 사용하였고, 상용 소프트웨어 FEKO^[8]의 MoM에서 단일 안테나 해석을 수행하였다. 해석에 사용한 Blade 다이폴 안테나 형상은 그림 2와 같고, 반사손실은 그림 3에 나타내었다. 안테나의 임피던스 및 전류는 MoM 결과로 구할 수 있다. 예를 들면 800 MHz에서 V₁₁=1 V로 가정하면 Z₁₁= 63.259 +j13.1415 Ω 및 I₁₁=0.01515−j0.0031481A를 얻을 수 있고, 본 연구에서는 급전 임피던스를 Z₀=50Ω으로 가정하였다.

그림 2. | Fig. 2. Blade 안테나 형상(크기: 244 mm×140 mm) | Geometry of Blade antenna (size: 244 mm×140 mm).

Download Original Figure

그림 3. | Fig. 3. Blade 안테나 반사 손실 | Return loss of Blade antenna.

Download Original Figure

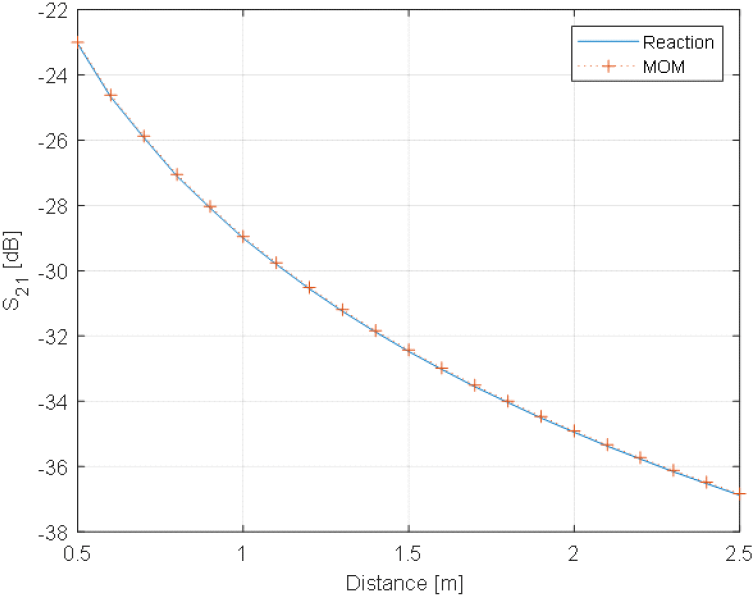
두 개의 Blade 안테나간 간섭도 계산을 거리에 따라 수행하였다. 간섭도 계산 상황은 그림 4에 나타내었다. 두 개의 안테나 간 거리는 0.5 m부터 2.5 m까지 0.1 m 간격으로 간섭도를 계산하였고, 이때 주파수는 800 MHz로 설정하였다. 간섭도 결과는 그림 5에 도시하였다. MoM 결과와 reaction을 이용한 거리별 간섭도 결과는 거의 일치하는 것을 확인할 수 있다.

그림 4. | Fig. 4. 안테나 간섭도 계산 모델 | Configuration for calculation of coupling between Blade antennas.

Download Original Figure

그림 5. | Fig. 5. Blade 안테나 간 거리에 따른 간섭도 비교 | Comparison of coupling vs. distance between Blade antennas.

Download Original Figure

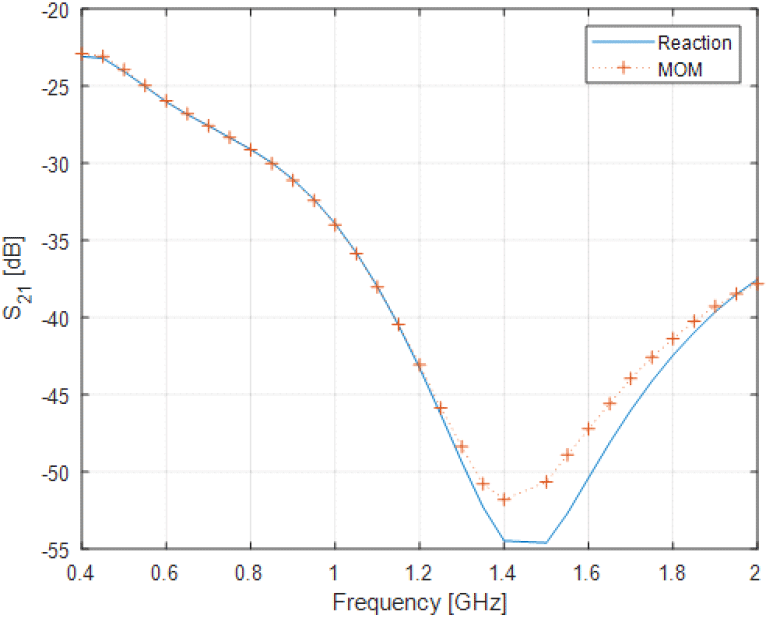
다음은 동일한 환경에서 거리를 1 m로 고정하고, 주파수 400 MHz부터 2 GHz까지 50 MHz 간격으로 주파수별 간섭도를 계산하였다. 결과는 그림 6에 나타내었다. Reation 방법을 이용한 주파수별 간섭도 계산 결과는 MOM 결과와 매우 유사함을 확인하였다.

그림 6. | Fig. 6. Blade 안테나 간 주파수별 간섭도 계산(안테나 간 거리: 1 m) | Comparison of coupling vs. frequency (distance: 1 m).

Download Original Figure

다음으로는 동일 안테나가 아닌 Blade 안테나와 0.1 m 길이의 wire dipole 안테나 간의 상대 거리별 간섭도를 계산하였다. 해석 환경은 그림 7에 표시하였고, 해석 주파수는 800 MHz로 계산 결과는 그림 8에 나타내었다. Blade 안테나와 wire dipole 안테나 간의 reaction을 이용한 간섭도 계산 결과도 MoM 해석 결과와 매우 유사함을 확인하였다.

그림 7. | Fig. 7. Blade 안테나와 wire dipole 안테나 간섭도 계산 환경 | Configuration for calculation of coupling between Blade and wire antenna.

Download Original Figure

그림 8. | Fig. 8. Blade 안테나와 wire dipole 안테나 간섭도 계산 간섭도 계산(주파수 800 MHz) | Comparison of coupling vs. distance between Blade and wire antenna (frequency: 800 MHz).

Download Original Figure

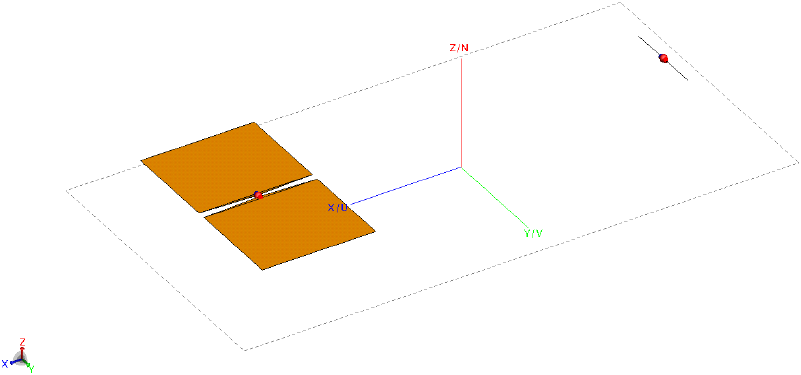
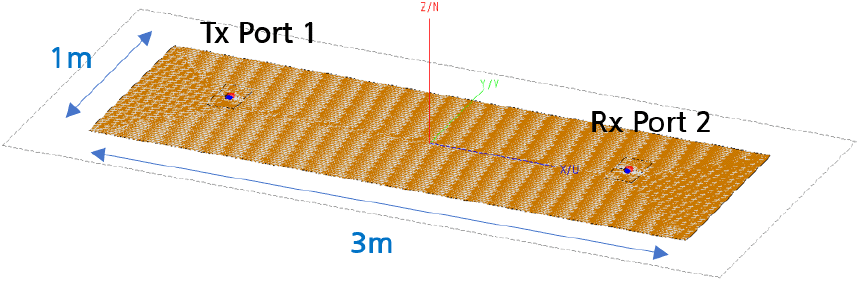
다음은 그림 9와 같이 두 안테나가 완전 도체 위에 놓여 있는 경우를 고려하였다. 이때 안테나는 도체 평판으로부터 0.05 m 높이에 위치한다. 해당 환경에서 full wave 해석으로 MLFMM(multi-level fast multipole method)으로 사용하였고, MLFMM의 경우 유한 평면까지 이산화(discretization)하여 두 안테나 사이의 간섭도를 계산하였다. 제안된 방법인 경우, 유한도체를 무한도체로 가정하고 image theory를 써서 도체에 의한 필드 계산을 근사화하였다. 전과 같은 Blade 다이폴 안테나를 도체 위 0.05 m에 위치시켰다.

그림 9. | Fig. 9. 동일 평면상에 배치된 안테나 간 간섭도 계산 모델 | Geometry for calculation of coupling between antennas over conducting plate.

Download Original Figure

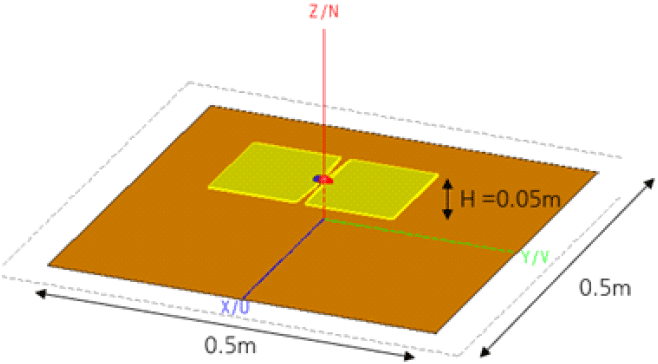
이때, 안테나의 특성은 도체의 효과로 자유공간에 있는 경우(그림 3)와 다르게 된다. 완전도체 평면에 의해 특성이 변화하기 때문에, 그림 10과 같이 Blade 다이폴 안테나를 도체의 일부(0.5 m×0.5 m 평면) 위 0.05 m에 위치시키고 단일 안테나의 특성을 계산하였다. 반사 특성은 그림 5와 같이 보이고 대역폭이 좁아지며, 중심 주파수가 900 MHz로 이동한 것을 확인할 수 있다.

그림 10. | Fig. 10. 플랫폼과 Blade 다이폴 안테나 | Blade antenna over platform.

Download Original Figure

제안된 reaction 방법은 무한 도체 평판을 가정하기 위해서 그림 11에서 보듯이 두 안테나 사이는 자유공간이고, image theory를 사용해야 하므로 Tx인 안테나 1은 박스가 두 부분으로 나뉘어진다. 위 박스는 자유공간 방사, 아래 박스는 image source 방사로 나뉜다. 수신 안테나를 감싸는 박스는 안테나 부분만 감싸는 박스로 선택하였다. 만약 밑 평면의 크기가 크고, 안테나가 평면의 가상자리 가까이에 놓여 있지 않으면 가상자리 회절 효과가 적어 image theory의 정확도가 매우 높다.

그림 11. | Fig. 11. 동일 평면에 배치된 안테나 간 간섭도 계산 개념도 | Configuration of coupling between antenna over conducting plate.

Download Original Figure

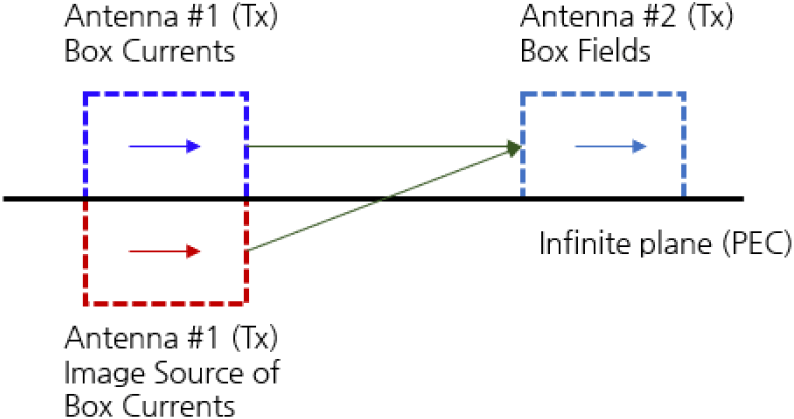
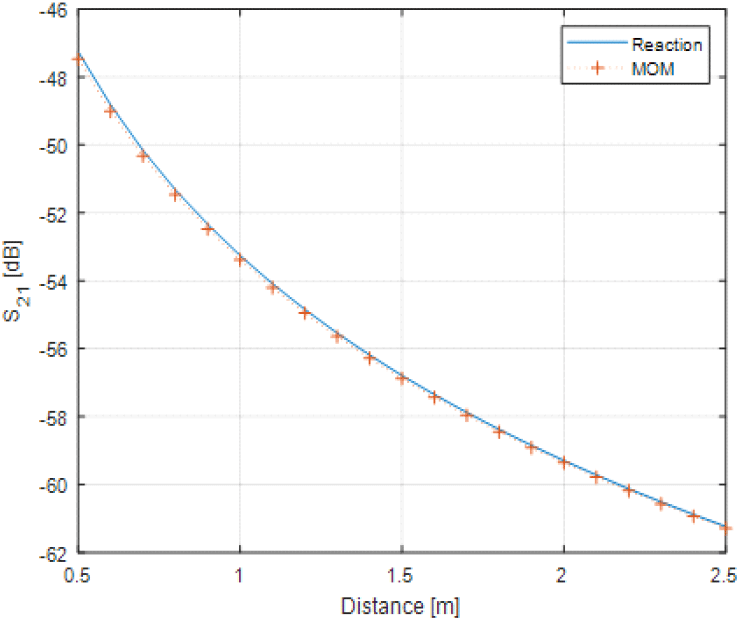
그림 12에는 유한 평판 플랫폼 위에 배치한 두 개 Blade 안테나 간의 간섭도 계산을 상대 거리 0.5 m부터 2.5 m까지 0.1 m 간격으로 수행한 결과를 도시하였다. 이때 주파수는 도체 평면 효과에 의해 이동한 중심 주파수 900 MHz를 사용하였다. 거리가 멀어지면 안테나가 평면 가장자리와 가까워져 이의 효과로 MLFMM 결과에서 진동이 발생하나 전반적으로 reaction 방법의 정확도는 매우 높음을 알 수 있다.

그림 12. | Fig. 12. 평판 플랫폼 위의 Blade 안테나 간 거리별 간섭도 계산(주파수: 900 MHz) | Comparison of coupling between Blade antennas located over conducting plate vs. distance between antennas (frequency: 900 MHz).

Download Original Figure

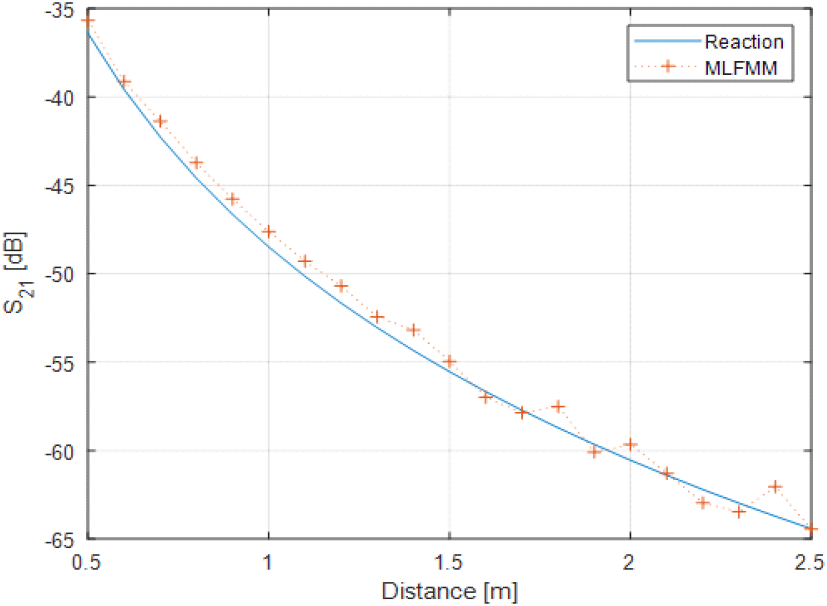
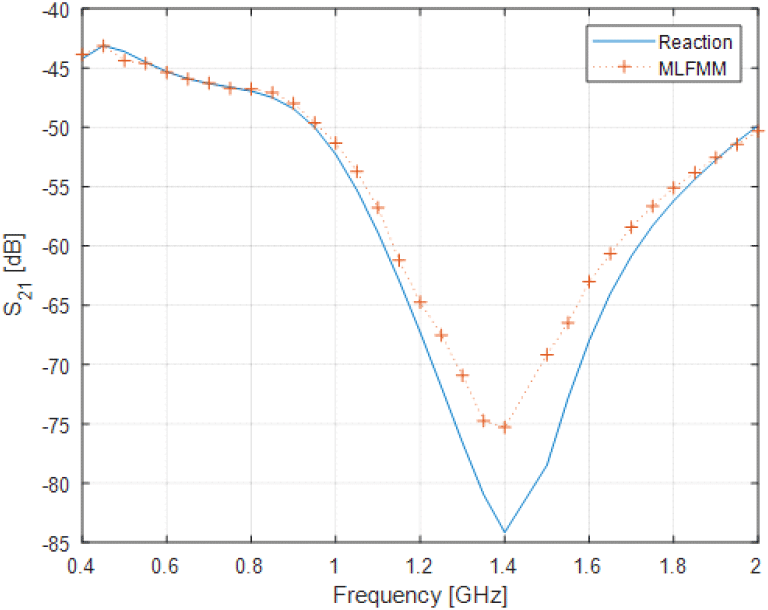
다음은 동일한 환경에서 거리를 1 m로 고정하고 주파수 400 MHz부터 2 GHz까지 50 MHz 간격으로 주파수별 간섭도를 계산하였다. 결과는 그림 13에 나타내었다. Reaction 방법을 이용한 주파수별 간섭도 계산 결과는 MLFMM 결과와 유사하게 나타나는 것을 확인하였다. 그림 9와 같은 조건에서 주파수 2 GHz 기준으로 FEKO(ver. 2018.1) MLFMM 해석 시간은 총 322초가 소요되었다. 이때 격자수는 36,364개였고, 사용한 CPU는 Intel(R) Xeon (R) E5-2683 v4 @ 2.10 GHz이고, 싱글코어 해석을 수행하였다. 동일한 해석 환경에서 안테나 격자 전류를 이용한 reaction 해석은 MATLAB(ver. R2021a)에서 46초가 소요되었다. 이때 평판 플랫폼의 크기를 키우고 안테나 간 거리를 멀게 할수록 FEKO는 격자 수 증가로 인해 해석 시간이 증가하게 되지만, reaction 방법은 연산량이 동일하기 때문에 일정한 해석 시간을 갖는 장점이 있다.

그림 13. | Fig. 13. 평판 플랫폼 위의 Blade 안테나 간 주파수별 간섭도 계산(거리: 1 m) | Comparison of coupling between Blade antennas located over conducting plate vs. frequency (distance: 1 m).

Download Original Figure

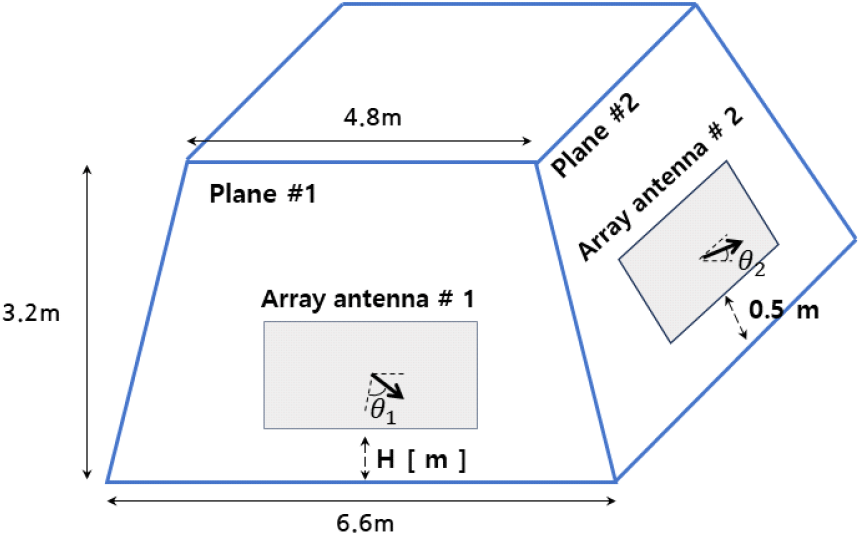
다음은 통합마스트 옆면 간 배열 안테나 간섭도 계산을 고려한다. 해석에 이용할 통합 마스트 구조는 그림 14와 같다. 통합마스트를 모사한 사각뿔대의 재질은 완전도체를 가정한다. 2차원 배열 안테나는 x축과 y축 방향으로 각각 N개, M개, dx, dy 간격으로 균일하게 안테나 소자를 배치하여 구성한다^[9]. 이때 (m, n)번째 안테나 소자의 amplitude는 I_mn이고, 모든 안테나 소자의 amplitude를 I₀로 고정하면 I_mn = I₀이다. 이때, array factor는 식 (8)과 같다.

A F = I 0 ∑ m = 1 M e j m − 1 k d x sin θ cos ϕ + β x ∑ n = 1 N e j n − 1 k d y sin θ cos ϕ + β y

(8)

그림 14. | Fig. 14. 통합마스트 형상과 배열안테나 배치도 | Geometry of integrated mast and array antenna position.

Download Original Figure

주 빔(main beam lobe) 방향을 θ=θ₀, ϕ=ϕ₀로 정하는 경우 β_x, β_y는 다음과 같은 값으로 결정할 수 있다.

β x = − k d x sin θ 0 cos ϕ 0 β y = − k d y sin θ 0 sin ϕ 0

(9)

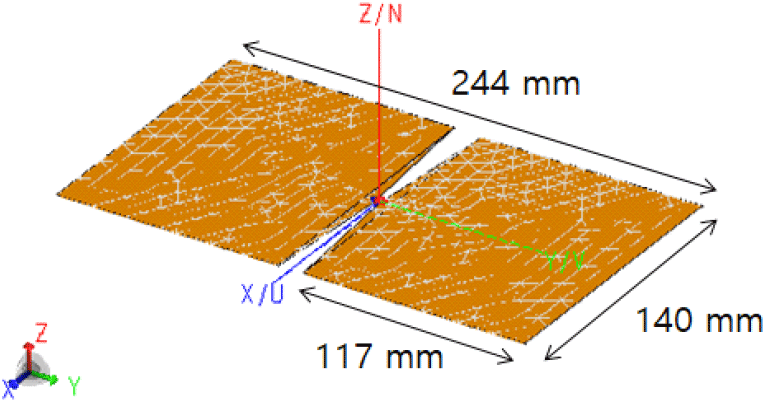
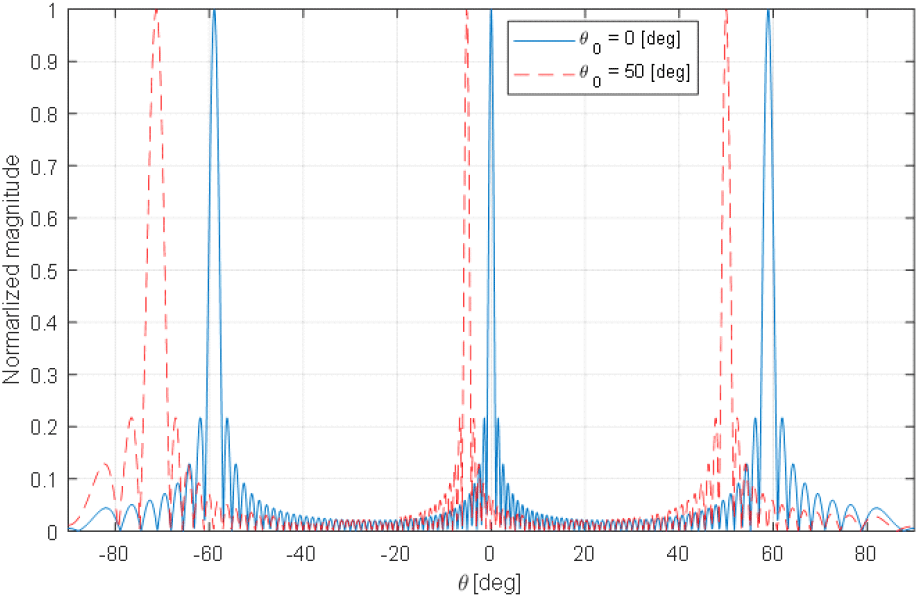
수치 실험에 사용할 2차원 배열 안테나 배치는 x축 방향으로 M=48개, y축 방향으로 N=32개 총 1,536개의 소자를 dx=dy=0.035 m 간격으로 배치하도록 한다. 2차원 배열 안테나의 전체 길이는 약 1.645 m×1.085 m가 된다. 여기서 안테나 기본 소자는 전기 수직 미소 다이폴을 사용한다. 주 빔 방향을 각각 ϕ₀=0°, θ₀=0°, 50°로 했을 때 각각의 2차원 배열 안테나의 ϕ₀=0일 때 θ에 따른 방사패턴은 다음 그림 15와 같이 나타난다. 설계한 배열 안테나의 특성상 방사패턴에 주 빔과 grating lobe가 나타나는 것을 확인할 수 있다.

그림 15. | Fig. 15. 배열 안테나의 방사 패턴(실선: 주 빔 방향 ϕ₀= 0°, θ₀=0°인 경우, 점선: 주 빔 방향 ϕ₀=0°, θ₀= 50°인 경우) | Radiation pattern of array (solid line: main beam direction, ϕ₀= 0°, θ₀=0°, dashed line: main beam direction, ϕ₀= 0°, θ₀=50°).

Download Original Figure

통합 마스트 해석에 사용할 수직 미소 다이폴은 평판 위 1 mm에 위치하고, 이때 reaction 계산 시 수신 안테나에 도달하는 송신 안테나의 전자기파 성분은 옆면의 wedge 모서리의 회절 성분만 존재한다. 실제로는 회절이 여러 모서리에서 발생할 수 있지만, 다른 모서리에서 발생하는 회절의 크기는 매우 작아, 그림 14의 평면 1과 평면 2의 모서리에 의한 1차 회절만을 고려한다. 본 논문에서는 회절 성분 계산에 UTD(uniform theory of diffraction)를 사용하였다^[10].

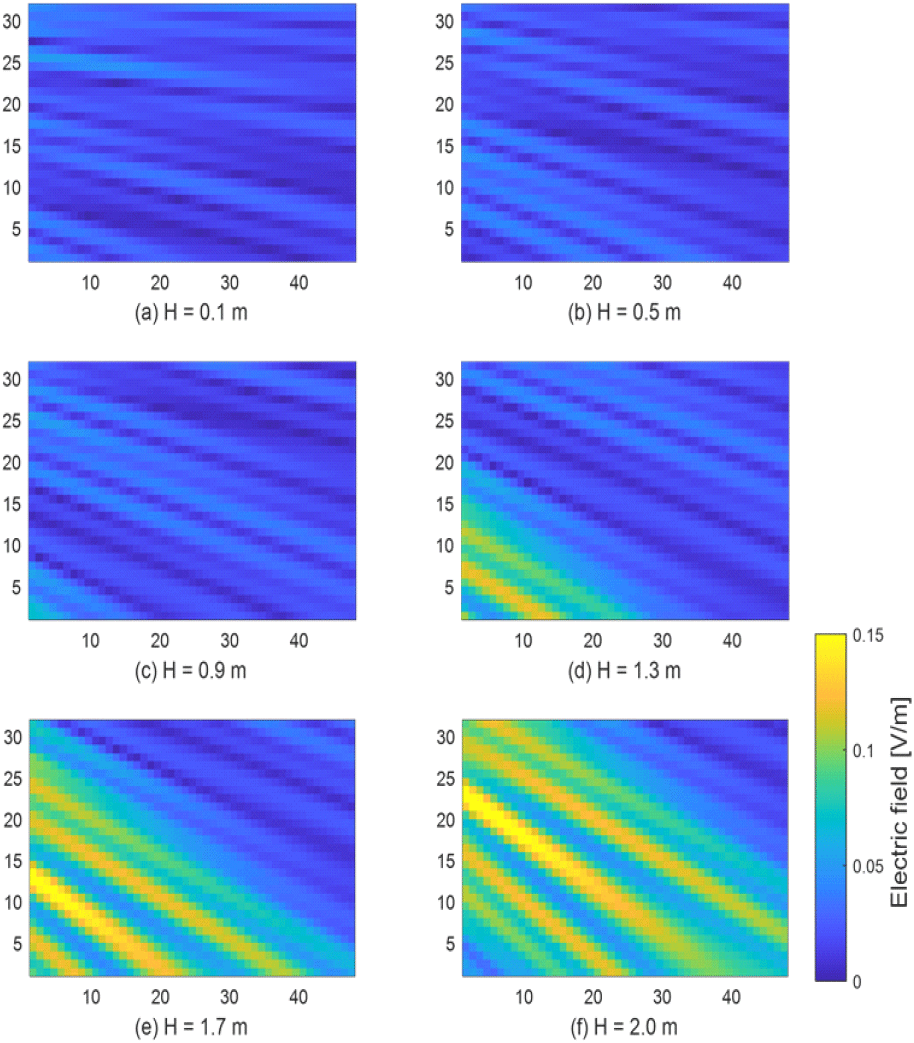
그림 14에서 배열 안테나 1의 통합마스트 바닥으로부터 높이 H를 변경하면서 배열 안테나 2의 수직 미소 다이폴 개별 위치에 수신하는 배열 안테나 1로부터 발생한 전기장 크기를 구해보면 그림 16과 같다. 이때 배열 안테나 2 방향으로 많은 에너지가 전송되도록, 배열 안테나 1의 주빔 방향을 ϕ₁=0°, θ₁=50°로 설정하였다. 높이 H가 높아짐에 따라서 전기장 크기가 변하여, reaction 또한 변할 것으로 예측된다.

그림 16. | Fig. 16. 배열 안테나 1의 높이 변화에 따른 배열 안테나 2에서 수신한 전기장 크기(배열 안테나 1의 높이: (a) H=0.1 m, (b) H=0.5 m, (c) H=0.9 m, (d) H=1.3 m, (e) H=1.7 m, (f) H=2.0 m) | Electric field intensity received by array 2 according to height of array antenna 1 (height of array antenna 1: (a) H=0.1 m, (b) H=0.5 m, (c) H=0.9 m, (d) H=1.3 m, (e) H=1.7 m, (f) H=2.0 m).

Download Original Figure

안테나 사이의 coupling은 reaction <2, 1>에 비례하므로 여기서는 <2, 1>을 계산하였다. Reaction <2, 1> 계산 시 J₂는 배열 안테나 2의 수직 미소 다이폴의 전류이고, 이때 M₂=0이므로, 식 3(b)는 식 (10)과 같이 간략하게 계산된다.

2, 1 = ∫ V 2 E 1 ⋅ J 2 d V

(10)

배열 안테나 1의 주 빔 방향(ϕ₁=0°, θ₁=50°)은 고정하고, 배열 안테나 2의 주 빔 방향을 ϕ₂=0°, θ₂=−50°~0°까지 변화시켰을 때, reaction값의 변화를 그림 17에 도시하였다. 배열 안테나 2의 주빔방향이 배열 안테나 1을 향한 경우(θ₂=−50°)에서 멀어지는 방향인 θ₂=0°까지 그래프의 경향은 reaction이 작아지는 경향이 있다. 하지만, θ₂= 0°주변에서 reaction이 다시 증가하는 추세를 보이는데, 이는 그림 15와 같이 설계한 배열 안테나의 패턴이 주빔방향이 θ₂=0°인 경우 grating lobe가 θ₂=−58°에서 존재해서 reaction의 값이 다시 커진다.

그림 17. | Fig. 17. 배열 안테나 2 주 빔 방향에 따른 reaction | Reaction vs. main beam direction of array 2.

Download Original Figure

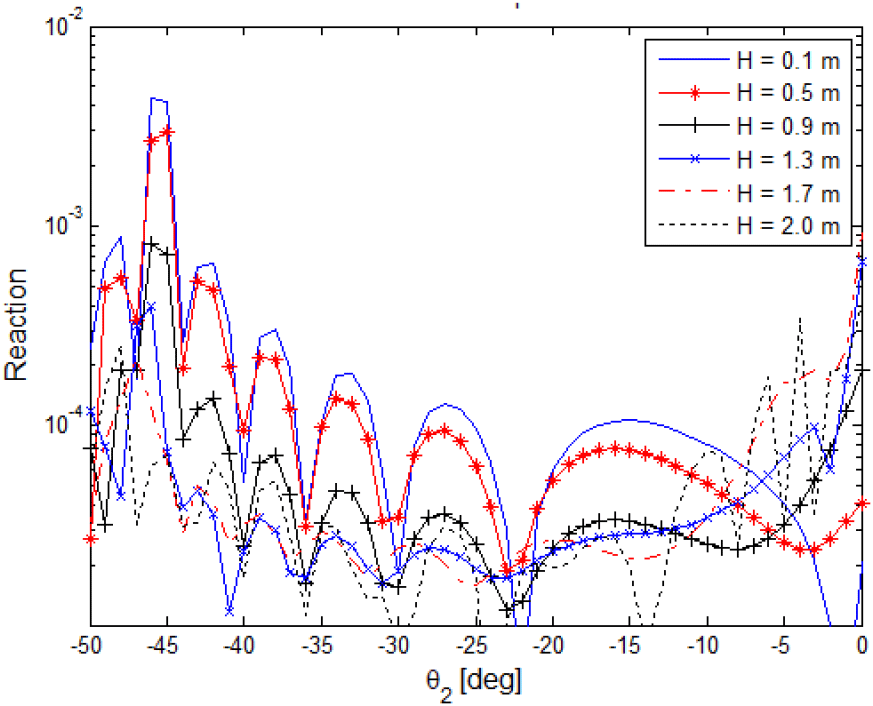
그러므로 제안된 reaction을 이용한 안테나 사이의 간섭도 계산방법은 정확도가 높고 계산시간이 매우 적어 효율적인 안테나 배치 등에 적용가능하다.

Ⅳ. 결 론

본 논문에서는 안테나 간 간섭도 계산에 reaction theorem을 적용하는 방법을 제안하였다. 이의 검증을 위해 blade 안테나와 wire 다이폴 안테나에 대해 full wave 해석 결과와 비교 검증하였다. 동일 평판의 플랫폼 효과는 image theory를 이용하였고, reaction 방법의 간섭도 계산 유용성을 검증하였다. 통합마스트의 이웃한 2면의 배열 안테나에 대한 reaction 계산은 수직 미소 다이폴로 구성된 2차원 배열 안테나를 가정하여 모서리 간 회절 성분을 이용하여 계산하여, 주 빔 방향에 따른 reaction 크기 변화를 살펴보았다. Reaction을 이용한 안테나 간섭도 계산은 개별 안테나의 full wave 해석 결과를 재활용할 수 있는 장점이 있어서, 안테나의 다양한 배치와 플랫폼에 대한 빠른 해석을 수행할 수 있어, 향후 안테나 최적 배치에 활용할 수 있을 것으로 기대된다.

Acknowledgements

이 논문은 2023년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(계약번호: UD210011DD).

References

[1].

H. P. Seo, K. H. Lee, “Integrated mast applied for improving stealth ship performance,” Journal of the Korea Association of Defense Industry Studies, vol. 22, no. 3, pp. 27-46, Sep. 2015.

[2].

S. W. Byun, H. J. Lee, and W. S. Nah, “Electromagnetic near-field coupling between antenna and transmission line: Analysis and modeling,” Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 7, pp. 541-553, Jul. 2023.

[3].

J. Richmond, “A reaction theorem and its application to antenna impedance calculations,” IRE Transactions on Antennas and Propagation, vol. 9, no. 6, pp. 515-520, Nov. 1961.

[4].

L. Johan, “Visualizing and controlling coupling paths between antennas installed on common platforms,” M.S. thesis, KTH School of Electrical Engineering and Computer Science, Stockholm, 2020.

[5].

J. Malmström, H. Holter, and B. L. G. Jonsson, “On mutual coupling and coupling paths between antennas using the reaction theorem,” IEEE Transactions on Electromagnetic Compatibility, vol. 60, no. 6, pp. 2037-2040, Dec. 2018.

[6].

D. M. Pozar, Microwave Engineering, 4th ed. New York, NY, John Wiley & Sons, 2005.

[7].

V. Iyer, S. Makarov, and F. Nekoogar, “On wideband modular design of small arrays of planar dipoles,” in 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Jul. 2010, pp. 1-4.