The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(7):541-553

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.7.541

논문/REGULAR PAPERS

안테나 근역장과 인접 전송선로와의 전자기 결합 분석에 대한 연구

변성완

, 이현재^*

, 나완수^*^,^†

Electromagnetic Near-Field Coupling between Antenna and Transmission Line: Analysis and Modeling

Sungwan Byun

, Hyun Jae Lee^*

, Wansoo Nah^*^,^†

성균관대학교 DMC공학과

^*성균관대학교 전자전기공학과

Department of Digital Media and Communications Engineering, Sungkyunkwan University

^*Department of Electrical and Computer Engineering, Sungkyunkwan University

^†Corresponding Author: Wansoo Nah (e-mail: wsnah@skku.edu)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: May 09, 2023; Revised: Jun 01, 2023; Accepted: Jul 19, 2023

Published Online: Jul 31, 2023

요 약

본 논문은 안테나 근역장에서 인접 전송선로로 전자기결합(coupling)되는 노이즈을 분석하는 방법을 제안하였다. 스마트폰에서 발생하는 안테나에서 인접 선로로의 노이즈 전달을 전자기장을 통해 유도된 전자기결합으로 보고 모델링하였다. 맥스웰 방정식과 전송선로 이론을 토대로, 근역장에서 노이즈 전달을 계산하는 모델을 제시하였다. 제시한 모델과 기존의 연구를 평면파에 의한 전자기 결합을 토대로 유효성을 확인했으며, 이를 바탕으로 근역장으로 확장하여 안테나와 피해 선로를 모델링하여 인접한 안테나에서 선로로 유기되는 노이즈 전달을 계산하였다. 안테나 근역장에서의 노이즈 전달은 3D EM simulation과 결과를 비교하여 유효성을 확인했다. 제안한 모델을 토대로 노이즈 계산 시, 3D 시뮬레이션 대비 70 %의 시간 절감효과가 있으며, 선로의 방향에 따른 노이즈 전달 차이에 대해서도 예측이 가능하다.

Abstract

In this paper, we propose a method to predict the interference from antenna near-field coupling to a nearby transmission line. It is assumed that the interference from the antenna to the nearby trace is an electromagnetic field that traces the coupling in a smartphone. Based on the Maxwell and telegrapher equations, a new model is proposed to calculate the noise transferred to the trace in the antenna near-field area. This was verified using plane-wave cases in prior research. Subsequently, the antenna and victim trace were designed to calculate the near-field noise. The proposed model shows a significantly similar result to that of the 3D EM simulation. It is especially notable not only it is able to save 70 % of time compared with 3D simulation, but also it is possible to predict how to reduce coupled noise by direction of trace.

Keywords: Near-Field Coupling; Electromagnetic Interference; Field to Trace Coupling; Radio Frequency Interference

Ⅰ. 서 론

스마트폰이 발전함에 따라 다양한 기능 및 RF(radio frequency) 관련 기능들이 집적화되고 있다. 스마트폰이라는 한정된 공간 내 카메라, 오디오 등 다양한 디지털 부품 및 다양한 RF 기능들이 모두 실장이 되어야 한다. 따라서, 안테나에서 방사되는 송신(Tx) 신호가 주변의 디지털 부품들에 영향을 주는 전자파 장해(electromagnetic interference) 이슈가 지속해서 발생하고 있다. 5G NR(new radio) 가 보편화되면서 모바일 단말 내 송신을 지원하는 안테나가 증가하고 있다. 5G와 기존 4G LTE(long term evolution)와 동시에 동작하는 EN-DC(E-UTRA NR dual connectivity)의 경우 LTE와 NR 신호가 동시에 송신된다^[1]. 또한, SRS(sounding reference signal)의 도입으로 스마트폰 내 NR을 지원하는 모든 안테나에서 신호를 송신할 수 있게 되었다^[2]. 이와 더불어 스마트폰 내 전자파 장해에 취약한 FPCB(flexible printed circuit board)가 증가하고 있다^[3]. FPCB는 유연하고 얇게 제작되어 메인 PCb(printed circuit board)가 커버하지 못하는 영역에서 주변부 부품과 연결이 필요할 때 많이 사용한다. 하지만, FPCB 구조는 차폐에 불리하여 전자파 장해에 상당히 취약하다^[4]. 앞서 기술한 바와 같이, 노이즈원인 송신 안테나의 증가와 전자파 장해에 취약한 FPCB의 증가가 복합적으로 작용하여, 스마트폰에서 송신신호에 의한 주변 디지털 신호의 왜곡 이슈가 심화하고 있다. 본 논문은 스마트폰에 주로 사용되는 FR1(frequency range 1) 대역^[5]의 5 GHz 이하의 주파수에서 안테나에서 송신되어 주변 전송선로로 미치는 영향을 분석하고자 한다.

외부인가 전자기장(electromagnetic field)의 전송선로 전자기결합에 관한 연구는 많이 이루어졌다. 참고문헌 ^[6]에서는 전송선로로 인가되는 전자기장에 의한 영향을 적분 수식으로 정리했다. 참고문헌 ^[7]~참고문헌 ^[9]의 경우 모두 외부에서 입사한 전자기파가 전자기결합하여 전송선로로 전달되는 노이즈를 미소 길이 등가 소스로 변환하였다. 이를 기반으로, PCB와 전체 길이에 대한 영향분석으로 확장한 연구가 순차적으로 진행되었다^[10],[11]. 하지만 기존 연구의 경우 외부에서 인가되는 전자기파를 평면파(planewave)만 대상으로 진행되었다. 평면파는 원역장(farfield)에서 전파된 필드로, 본 연구에서 주요한 노이즈원인 안테나 근역장(nearfield)에서 방사되는 노이즈에 대한 모델로는 사용될 수 없다. 따라서, 스마트폰 같은 복잡한 시스템에서 방사된 노이즈가 피해 경로로 전자기 결합되는 것에 대한 새로운 모델이 필요하다.

안테나 근역장에서 FPCB 전송선로로 전달되는 노이즈는 전자기장에 의한 전송선로 전자기 결합이 주요 전달 경로이다^[12]. 따라서 본 연구에서 주요 연구 대상은 송신 안테나로부터 방사된 잡음이 FPCB 전송선로에 유기된 전도성 노이즈이다. 다시 말해, 전자기장이 전송선로와 전자기 결합(field to trace coupling)한 방사 노이즈이다. 이를 위해 외부 전자기장에서 전자기 결합되어 유기된 노이즈의 모델링을 정립하고, 전송선로 양단으로 전달되는 전압, 전류를 예측해 보고자 한다. 특히, 스마트폰과 같이 복잡한 시스템에서 잡음원인 안테나에서 근역장 공간에서 인접 FPCB의 전송선로로 전자기 결합되는 노이즈를 빠르게 판단할 수 있는 모델을 제안하고자 한다.

Ⅱ. 외부 인가 전자기장에 의한 전송선로 전자기결합 이론

2-1 Taylor 모델^[7]

Taylor 모델은 전송선로의 미소 길이에서 외부 전자기장이 전송선로에 커플링되는 과정을 수식으로 전개한다. 맥스웰 방정식과 전송선로의 단위 길이당 R, L, G, C를 기반으로 하는 전송선로 이론을 통해 도출한다.

그림 1(a)는 두 개의 도체로 구성된 전송선로에 외부 필드가 인가되는 상황에 대한 모식도이다. 이를 그림 1(b)의 등가 회로로 변환하여 계산한다. 인가되는 외부 전자기장은 TEM(transverse electromagnetic) 파동이다. 이때 외부에서 인가되는 자기장 $H → i n c$ 와 전송선로의 전압 V(z,t), 전류 I(z,t)와 관계식은

δ V (z, t) δ z + r I (z, t) + l δ I (z, t) δ t = δ δ t ∫ a a ′ μ H → i n c ⋅ a → n d l = V F (z, t)

(1)

그림 1. | Fig. 1. 외부 전자기장에 의한 전송선로 전자기 결합 | Incident field to transmission line coupling.

Download Original Figure

이고, 외부에서 인가되는 전기장 $E → i n c$ 와의 관계식은

δ I (z, t) δ z + g V (z, t) + c δ V (z, t) δ t = − g ∫ a a ′ E → i n c ⋅ d l → − c δ δ t ∫ a a ′ E → i n c ⋅ d l → = I F (z, t)

(2)

이다. 식 (1) 및 식 (2)의 우변의 전압원 V_F (z,t), 전류원 I_F (z,t)는 외부에서 인가된 전자기장에 의해 유도된 전원이다. 본 논문에서 주파수로 분석하기 위해 페이저로 V_F (z), I_F (z)을 표현하면

V F (z) = j ω ∫ a a ′ μ H → i n c ⋅ a → n d l

(3)

I F (z) = − (g + j ω c) ∫ a a ′ E → i n c ⋅ d l →

(4)

이다.

2-2 C. R. Paul의 모델^[6]

미소 길이의 Taylor 모델의 분포된 노이즈원을 전체 길이로 확장하여 1개의 전압원, 전류원으로 대체한다. 식 (3) 및 식 (4)의 V_F (z), I_F (z)를 전체 길이에서 등가된 전압원을 V_FT (z), 전류원을 I_FT (z)라 한다. 이는 전송선로의 전달 행렬(chain matrix) Φ를 통해서 구할 수 있다.

그림 2는 전체 길이 l의 전송선로에서 외부 전자기장에 의해 유도된 각 1개의 전압원 V_FT (l), 전류원 I_FT (l)과 외부 전자기장에 영향이 없는 전송선로 구간으로 나누어 등가된 회로이다. 회로 좌측 끝단을 near end(ne), 우측 끝단을 far end(fe)라 명명한다.

V (l) I (l) = Φ 11 Φ 12 Φ 21 Φ 22 V (0) I (0) + V F T (l) I F T (l)

(5)

그림 2. | Fig. 2. 전체 전송선로에서 chain matrix와 외부 인가된 전자기장에 의해 유도된 전원의 등가회로 | Total length transmission line equivalent circuit with chain matrix form and induced sources by incident field.

Download Original Figure

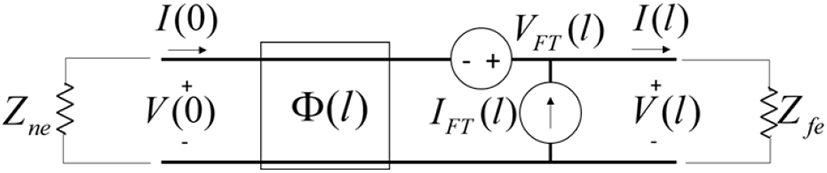
식 (5)는 그림 2를 수식화한 것이며, 식 (5)의 Φ 행렬의 각 항은

Φ 11 = e − γ l + e γ l 2 = cosh γ l Φ 21 = 1 2 Z 0 e − γ l − e γ l = − 1 Z 0 sinh γ l Φ 12 = Z 0 2 e − γ l − e γ l = − Z 0 sinh γ l Φ 22 = e − γ l + e γ l 2 = cosh γ l

(6)

이다. V_FT (l), I_FT (l)을 식 (6)을 이용해

V F T (l) = ∫ 0 l Φ 11 (l − τ) V F (τ) + Φ 12 (l − τ) I F (τ) d τ

(7)

I F T (l) = ∫ 0 l Φ 21 (l − τ) V F (τ) + Φ 22 (l − τ) I F (τ) d τ

(8)

으로 정리할 수 있다. 식 (7) 및 식 (8)과 동일하게, z=0일 때 등가 전원 V′_FT (l), I′_FT (l)를 구하면,

V ′ F T (l) = ∫ 0 l Φ 11 (− τ) V F (τ) + Φ 12 (− τ) I F (τ) d τ

(9)

I ′ F T (l) = ∫ 0 l Φ 21 (− τ) V F (τ) + Φ 22 (− τ) I F (τ) d τ

(10)

이다. 양 단의 전압, 전류를 구하기 위해 양 단의 임피던스를 고려해야 한다. 양 단의 전압, 전류 V(0), I(0), V(l), I(l)와 각 끝단의 임피던스 Z_ne, Z_fe 와의 관계는

V 0 = − Z n e I 0

(11)

V l = − Z f e I l

(12)

이고 이를 식 (5), 식 (11) 및 식 (12)와 연립하여 전류 I(0), I(l)로 정리하면

Z n e ϕ 11 + Z f e ϕ 22 − ϕ 12 − Z n e Z f e ϕ 21 I 0 = V F T l − Z f e I F T l

(13)

I l = I F T l + ϕ 22 − Z n e ϕ 21 I 0

(14)

가 된다. 위 식의 I(0) 앞의 항을 양변으로 나누어주고, 분모를 D로 정의하면, D, I(0)와 I(l)은 각각,

D = Z n e ϕ 11 + Z f e ϕ 22 − ϕ 12 − Z n e Z f e ϕ 21 = cosh γ l Z n e + Z f e + sinh γ l Z c + Z n e Z f e Z c

(15)

I 0 = V F T l − Z f e I F T l Z n e ϕ 11 + Z f e ϕ 22 − ϕ 12 − Z n e Z f e ϕ 21 = V F T l − Z L I F T l D

(16)

I l = V ′ F T l + Z n e I ′ F T l D

(17)

이다. 양 단 전압 V(0), V(l)은 식 (11), 식 (12), 식 (16) 및 식 (17)을 통해 구할 수 있으며, 이는

V 0 = − Z n e I 0 = − Z f e V F T l − Z L I F T l D

(18)

V l = Z f e I l = Z f e V ′ F T l + Z n e I ′ F T l D

(19)

이 된다.

2-3 각 모델의 장단점 및 수정된 근역장에 의한 전자기결합 모델 제안

기존의 연구는 공통적으로 전송선로의 특성을 알아야 분석할 수 있다. 또한, 외부에서 인가되는 전자기장에 의한 전자기결합을 계산하기 때문에, 외부에서 인가되는 전자기장의 크기와 방향을 알아야 계산할 수 있다.

C. R. Paul의 적분형 모델의 경우, 외부 전자기장에서 전자기 결합된 노이즈를 각 끝단의 한 개의 전압원, 전류원으로 등가한다. 대신 전자기장의 적분 계산이 필요하여, 인가된 전자기장을 계산할 수 있게끔 함수로 정확히 정의되어 있어야만 한다. 이러한 단점 때문에 근역장 상황에서는 이 모델을 적용하지 못한다.

Taylor 모델의 경우, 외부 전자기장에서 전자기 결합된 노이즈를 분포된 등가 전압원, 전류원으로 대체한다. 이 분포된 전압원, 전류원과 전송선로의 R,L,G,C항을 통한 회로 모델링을 통해서 각 끝단에 전달되는 노이즈를 구한다. 따라서 안테나 근역장에서의 전자기장 값을 입력하여 계산이 가능하다. 하지만, 미소 셀을 모두 회로모델링으로 구현해야 하기 때문에 시간이 많이 소요된다.

본 논문에서 제안하는 모델에서는 안테나의 근역장 커플링의 계산을 위해서, C. R. Paul의 수식 모델을 간단히 곱과 합으로 근사한다. 유전체의 높이는 아주 작아 동일한 전자기장이 분포한다고 근사가 가능하며, 분석 주파수 파장 대비 충분히 작은 미소 길이로 쪼개면 해당 길이도 동일한 전자기장이 분포한다고 가정할 수 있다. 그리고 Taylor 모델과 달리 전송선로의 전달 행렬 Φ를 활용하여 양 단의 1개의 전압원, 전류원으로 등가하여 계산한다. 이를 통해서 간단하고 빠르게 전송선로 양 끝단으로 전달되는 안테나 근역장 상황에서의 전자기 결합된 노이즈 전달을 계산할 수 있다. 이를 위해 작은 미소 길이로 선로를 나눈다. 이 때 해당 미소 길이에서는 동일한 전자기장이 인가되었다고 근사하여 전자기 결합된 노이즈원을 계산을 한다. 따라서, 식 (3) 및 식 (4)는 각각

V F z = j ω μ H x z h

(20)

I F z = − j ω c E y z h

(21)

으로 변경해 계산한다. H_x (z), E_y (z)는 그림 3(a)의 임의의 z값 위치에서 외부에서 인가된 자기장과 전기장이며, h는 두 도선 사이 높이이다. 그리고 식 (5), 식 (7) 및 식 (8)을 수정하여 전체길이의 전자기장에서 유도된 전압원, 전류원으로 대체하여 각 끝단에 전달되는 전압, 전류를 계산한다. 본 연구에서 미소 길이는 1 mm로 상정한다. 그리고 주파수는 0~5 GHz 범위에서 분석할 예정이다.

그림 3. | Fig. 3. 임의의 z 위치에서 외부 전자기장에 의한 전송선로 전자기 결합 | Incident field to transmission line coupling at an arbitrary z point.

Download Original Figure

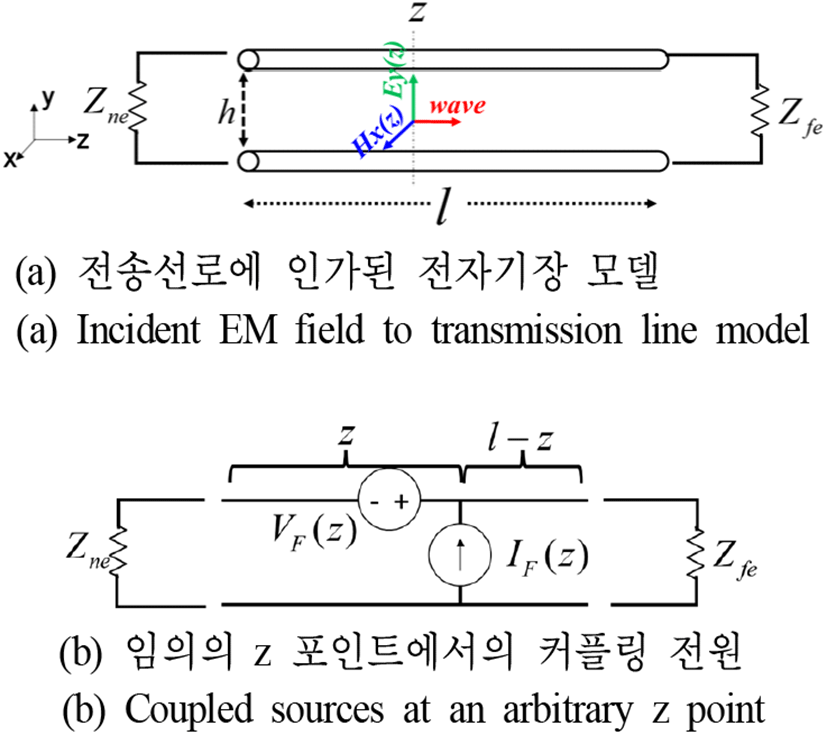
z=0위치를 ne(near end), z=l에서의 위치를 fe(far end)라 칭한다. 그림 3(b)의 미소길이 z위치에서 외부 전자기장 커플링으로 유도되는 미소 분산 전원V_F (z), I_F (z)을 양 단의 전원으로 등가한 전원을 각각ΔV_FT, ΔI_FT, ΔV′_FT, ΔI′_FT라 한다. 각각은 식 (5)를 통해

Δ V F T = Φ 11 l − z V F z + Φ 12 l − z I F z

(22)

Δ I F T = Φ 21 l − z V F z + Φ 22 l − z I F z

(23)

Δ V ′ F T = Φ 11 − z V ′ F z + Φ 12 − z I ′ F z

(24)

Δ I ′ F T = Φ 21 − z V ′ F z + Φ 22 − z I ′ F z

(25)

으로 구할 수 있다. Near end와 far end에서 등가된 전체 전압원 V_FT, I_FT, V′_FT, I′_FT는 모든 길이에서의 ΔV_FT, ΔI_FT, ΔV′_FT, ΔI′_FT의 전체 합이다. 다시 말해, Δz에 대해서 ΔV_FT, ΔI_FT, ΔV′_FT, ΔI′_FT 를 z=0부터 z=l까지 값들을 합한 것이다. 곧,

V F T = ∑ z = 0 l Δ V F T z Δ z

(26)

I F T = ∑ z = 0 l Δ I F T z Δ z

(27)

V ′ F T = ∑ z = 0 l Δ V ′ F T z Δ z

(28)

I ′ F T = ∑ z = 0 l Δ I ′ F T z Δ z

(29)

이다. V(0), I(0), V(l), I(l)은 식 (16), 식 (17), 식 (18) 및 식 (19)를 통해 D와 Z_ne, Z_fe를 통해 계산할 수 있다.

Ⅲ. 평면파에 의한 전자기 결합 모델 분석

3-1 피해 전송선로 모델링

평면파 및 안테나 근역장 조건에서 피해 FPCB의 모델 링이다.

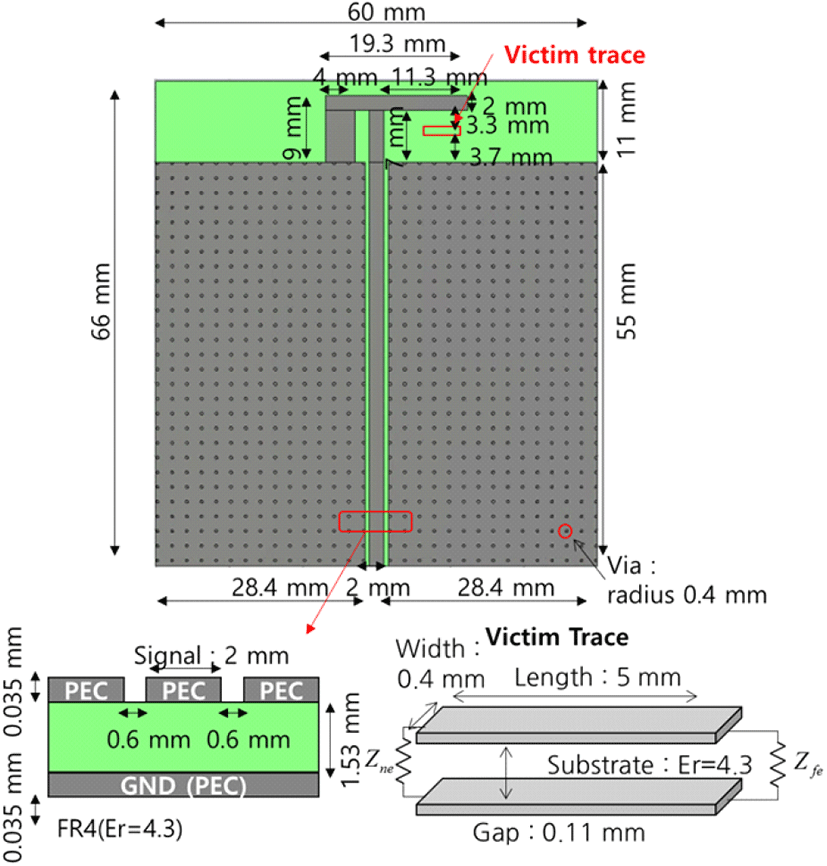
그림 4와 같이 신호(signal)선로와 기준접지(reference ground)선로의 너비가 동일하게 설계하였다. 선로의 너비는 0.4 mm, 두 개 도선 사이의 높이는 0.11 mm이다. 각 선로의 두께는 0.012 mm이다. 전체 선로 길이 5 mm이다. 도체는 PEC(perfect electronic conductor)로 설정했으며, 유전체의 상대유전율은 4.3이다. 이때 유전체는 감쇄 없이 설정했다. 따라서, 전송선로의 R, G값은 모두 0이다. 이 전송선로의 단위 길이당 커패시턴스와 단위 길이당 인덕턴스, 특성 임피던스는 표 1에 명기하였다. 각각 near end, far end의 부하 저항은 50 Ω으로 설정하였다.

그림 4. | Fig. 4. 피해 전송선로 모델링 | Victim trace modeling.

Download Original Figure

표 1. | Table 1. 설계한 선로의 특성 파라미터 | Characteristic parameters of designed trace.

c	1.38×10⁻¹⁰ F/m
l	3.46×10⁻⁷ H/m
Z ₀	50 Ω

Download Excel Table

3-2 평면파 3가지 인가방향에 따른 전자기 결합분석

C. R. Paul 모델, Taylor 모델, 그리고 본 논문에서 제안하는 3가지 모델에 대해서 평면파 입사 시 정합성을 확인하였다. 그림 5와 같이 3가지 케이스로 구분하며, 각각 평면파의 입사방향에 따라 sidefire, broadfire, endfire로 구분한다.

그림 5. | Fig. 5. 방향에 따른 3가지 평면파 인가 조건 | 3 cases of field excitation according to direction of planewave.

Download Original Figure

본 논문에서 제안하는 모델에서 전자기장 데이터를 추출하는 포인트는 각각 0.5 mm~4.5 mm까지 1 mm 단위로 5개 포인트에 CST의 field probe 기능으로 추출하였다.

3-2-1 Sidefire

Sidefire의 경우, 그림 5(a)와 같이 평면파가 접지면에서 신호면 방향로 진행하는 경우이다. 평면파의 전파방향은 +y 방향이며, 자기장은 −x 방향으로, 전기장은 +z 방향으로 진동한다. 이 때 선로에 전자기 결합되는 전자기장은 자기장이 우세하다.

그림 6(a) 및 그림 6(d)는 sidefire 케이스에 대한 far end에서의 전압, 전류 결과이다. 3가지 모델 모두 높은 정합성을 보여준다. 인가된 전자기장에서 자기장만 영향을 주어, 식 (3)의 노이즈 전압원 V_F (z)만 존재한다. 따라서, 도선을 따라 노이즈 전압원의 방향에 따른 전류만 유도된다. 이에 따라 V(0), V(l)의 위상은 180도 차이가 나고, 크기는 동일하다. 전류는 양 단 모두 크기, 위상이 동일하다.

그림 6. | Fig. 6. 평면파 인가 시, 제안한 모델, Taylor 모델, C.R.Paul 모델로 계산한 far end의 노이즈 전달 전압, 전류 | In case of incident planewave, voltage and current at the far end of trace calculated by proposed model, Taylor model, C.R.Paul model.

Download Original Figure

3-2-2 Broadfire

Broadfire의 경우에는 그림 5(b)와 같이 평면파가 선로의 옆에서 뚫고 진행하는 경우이다. 평면파 전파 방향은 −x 방향이며, 자기장 +z 방향으로 진동하며, 전기장의 경우에는 +y 방향으로 진동한다. 이 경우에는 전기장이 노이즈 전달에 우세하다.

그림 6(b) 및 그림 6(e)는 broadfire 케이스에 대한 far end의 전압, 전류 결과이며, 3가지 모델 모두 정합성이 높다. 전기장만 도선에 유도되어 식 (4)의 I_F (z)만 도선 사이에 존재한다. 따라서, 신호면에서 접지면으로만 전류가 흐르게 된다. 이 결과로 양단의 전류는 동일 크기, 180도 반대되는 위상을, 전압은 양단 모두 동일 크기, 동일 위상을 갖는다.

3-2-3 Endfire

마지막으로 endifre의 경우에는 그림 5(c)와 같이 평면파가 near end 방향에서 far end로 진행하는 경우이다. 평면파의 전파 방향은 +z 방향이다. 자기장은 +x 방향으로, 전기장은 −y 방향으로 진동한다. Endfire의 경우에는 전기장, 자기장 모두 전자기 결합에 영향을 준다.

그림 6(c) 및 그림 6(f)는 endfire 케이스의 far end에서의 전압, 전류 결과이다. 3가지 모델 정합성이 좋다. 이 경우에는 전기장, 자기장이 모두 도선에 노이즈로 유도된다. 또한, near end 방향에서 전자기장이 입사되어, far end로 전파되기 때문에 V(0), I(0) 크기가 V(l), I(l) 대비 더 크다. 또한, 위상은 도선의 길이의 영향만큼 변하게 된다.

Ⅳ. 안테나 근역장에 의한 전송선로 전자기 결합 분석

4-1 안테나 및 피해 전송선로 모델링

스마트폰의 안테나에서 신호가 송신될 때, 주변부의 FPCB에 유도되는 노이즈를 모사하기 위해, 간단한 안테나 및 피해 전송선로를 설계한다.

4-1-1 PIFA(Plannar Inverted F Antenna) 모델링

노이즈원(aggressor)으로 동작하는 안테나로 PIFA를 설계한다. 안테나는 PCB에서 50 Ω 전송선로로 급전되는 구조로 설계한다. 50 Ω으로 정합된 급전부에서 신호를 송신한다. 이 때, 안테나 주변에 전자기장을 형성하며, 이에 전자기 결합되어 인접한 피해 선로로 노이즈가 전달된다.

그림 7과 같이 가로 60 mm, 세로 66 mm의 2층 PCB 기판 위 PIFA 형태의 안테나를 그린다. PCB 기반에서 안테나로 급전되는 선로는 2 mm 너비의 CPW(coplanar waveguide)로 설계하며, 1층은 signal, 2층은 ground로 설계한다. 도선은 PEC, 유전체는 상대유전율 4.3의 무손실로 설정한다.

그림 7. | Fig. 7. PIFA 상세 치수 도면 | PIFA detailed dimension.

Download Original Figure

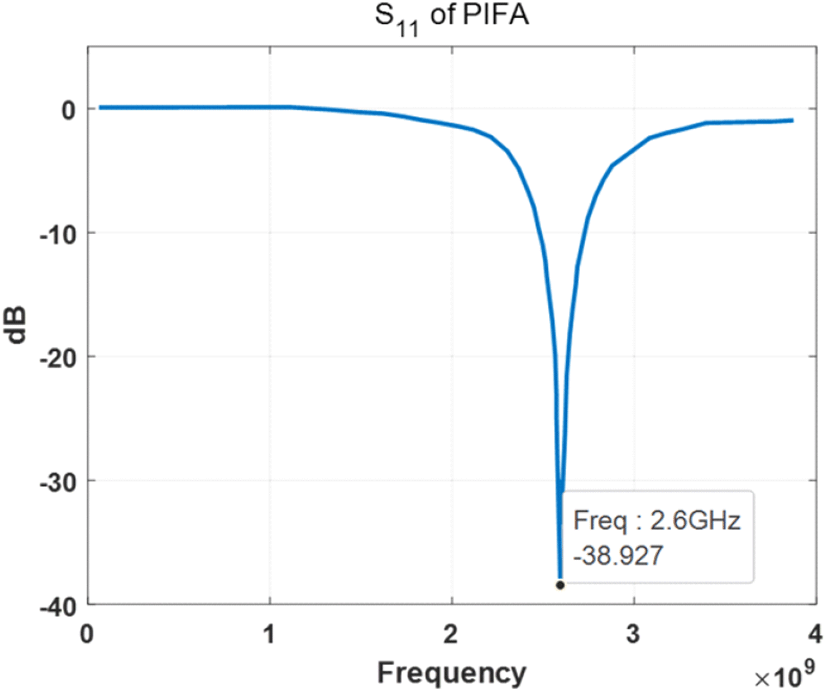
이 안테나의 공진은 그림 8의 S_11데이터처럼 2.6 GHz에 존재하며, −39 dB 의 공진을 갖고 있다. 2.6 GHz는 스마트폰에서도 주로 사용하는 주파수이다. NR대역 기준, n7의 경우 Tx 주파수는 2.5 GHz~2.57 GHz이고, n41의 경우 2.496 GHz~2.690 GHz이다.

그림 8. | Fig. 8. 설계한 PIFA의 S₁₁ | S₁₁ of designed PIFA.

Download Original Figure

4-1-2 피해 전송선로 모델링

피해 전송선로는 앞서 평면파 입사 시 확인했던 그림 4 와 동일한 선로를 사용했다. 안테나 근역장에서는 평면파와 다르게 전 방향으로 전자기장이 분포하기 때문에, 안테나 근역장 모델에서는 식 (20) 및 식 (21)처럼 선로에 영향을 미치는 전자기장만을 추출하여 계산을 진행한다. 그림 9와 같이 선로 내부에 5개 포인트에서 전자기장 데이터를 추출해 계산을 진행했다.

그림 9. | Fig. 9. 설계한 피해선로의 전자기장 데이터 추출 위치 | Locations of field data extracted in designed victim transmission line.

Download Original Figure

그림 10은 안테나로 신호를 인가하였을 때, 전기장, 자기장의 분포 그림이다. 그림 10(a)와 같이, 전기장은 피해선로를 배치한 구간에서 안테나에서 PCB의 접지 방향으로 강하게 분포한다. 그림 10(b)처럼 자기장은 PCB 방향에 수직하여 입사되는 방향으로 강하게 분포한다. 전 주파수 대역에서의 전자기장 분포를 확인하기 위해, 그림 9의 위치에서 데이터를 비교해 봤다.

그림 10. | Fig. 10. PIFA의 2.6 GHz에서 전기장, 자기장 분포 | E-field, H-field plot of PIFA at 2.6 GHz.

Download Original Figure

그림 11은 5 mm 선로의 끝에서 0.5 mm 떨어진 위치부터 1 mm씩 위치를 떨어진 5개의 포인트의 전자기장의 세기를 추출한 데이터이다. 그림 11(a)는 전기장의 크기이며, 그림 11(b)는 자기장의 크기이다. 각 전자기장의 세기가 가장 크게 영향을 받는 선로의 배치를 최대 전자기 결합 배치라 하고, 전자기장에 가장 작게 영향을 받는 선로의 배치를 최소 전자기 결합 배치라 하며, 두 가지 경우를 비교 분석해 보고자 한다. 전기장은 y 축>x축>z 축 순으로 강하게 분포하며, 자기장은 z 축>x 축>y 축 순으로 강하게 분포한다. 따라서, worst case는 전기장이 y축, 자기장이 z축에 영향을 받는 배치이고, best case는 전기장이 z축, 자기장이 y축에 영향을 받는 배치이다.

그림 11. | Fig. 11. 에서 추출한 5개 위치에서의 각 축별 필드 세기 분포 | Field magnitude distribution by axis based on .

Download Original Figure

4-2 안테나 근역장 2가지 케이스 분석

앞서 기술한 대로, 최대 전자기 결합 배치와 최소 전자기 결합 배치로 구분하여 CST EM 시뮬레이션 결과와 비교 분석을 진행한다. 최대 전자기 결합 배치와 최소 전자기 결합 배치의 차이점은 x축 기준 90도로 선로 방향만 바꾼 배치이다.

4-2-1 최대 전자기 결합 배치(Most Coupled Case)

최대 전자기 결합 배치는 그림 12와 같이 xz 평면에 수평으로 하여 2개의 도선이 배치되고, 전체 선로는 +x축 방향으로 진행하는 배치이다. 이 배치에서 외부 전자기장에 의한 전자기 결합의 경우, 전기장은 y축 방향에 영향을 받고, 자기장은 z축 방향에 영향을 받는다.

그림 12. | Fig. 12. 최대 전자기 결합 배치 위치 | Location of most coupled case.

Download Original Figure

그림 13에서 파란색과 빨간색의 far end, near end값은 본 논문에서 제안한 모델로 계산한 값이다. 노란색, 보라색 결과값은 CST EM 시뮬레이션을 통해 추출한 값이다. 전자기 결합으로 전달되는 최대값은 2.8 GHz에서 −21.7 dBV, 전류는 −55.7 dBA만큼 전달된다.

그림 13. | Fig. 13. 최대 전자기 결합 배치의 양 단에서 제안한 모델과 CST의 (a) 전압 세기, (b) 전압 위상, (c) 전류 세기, (d) 전류 위상 결과 비교 | Comparison of (a) voltage magnitude, (b) voltage phase, (c) current magnitude, (d) current phase results from proposed model and CST of each ends of trace in most coupled case.

Download Original Figure

4-2-2 최소 전자기 결합 배치(Least Coupled Case)

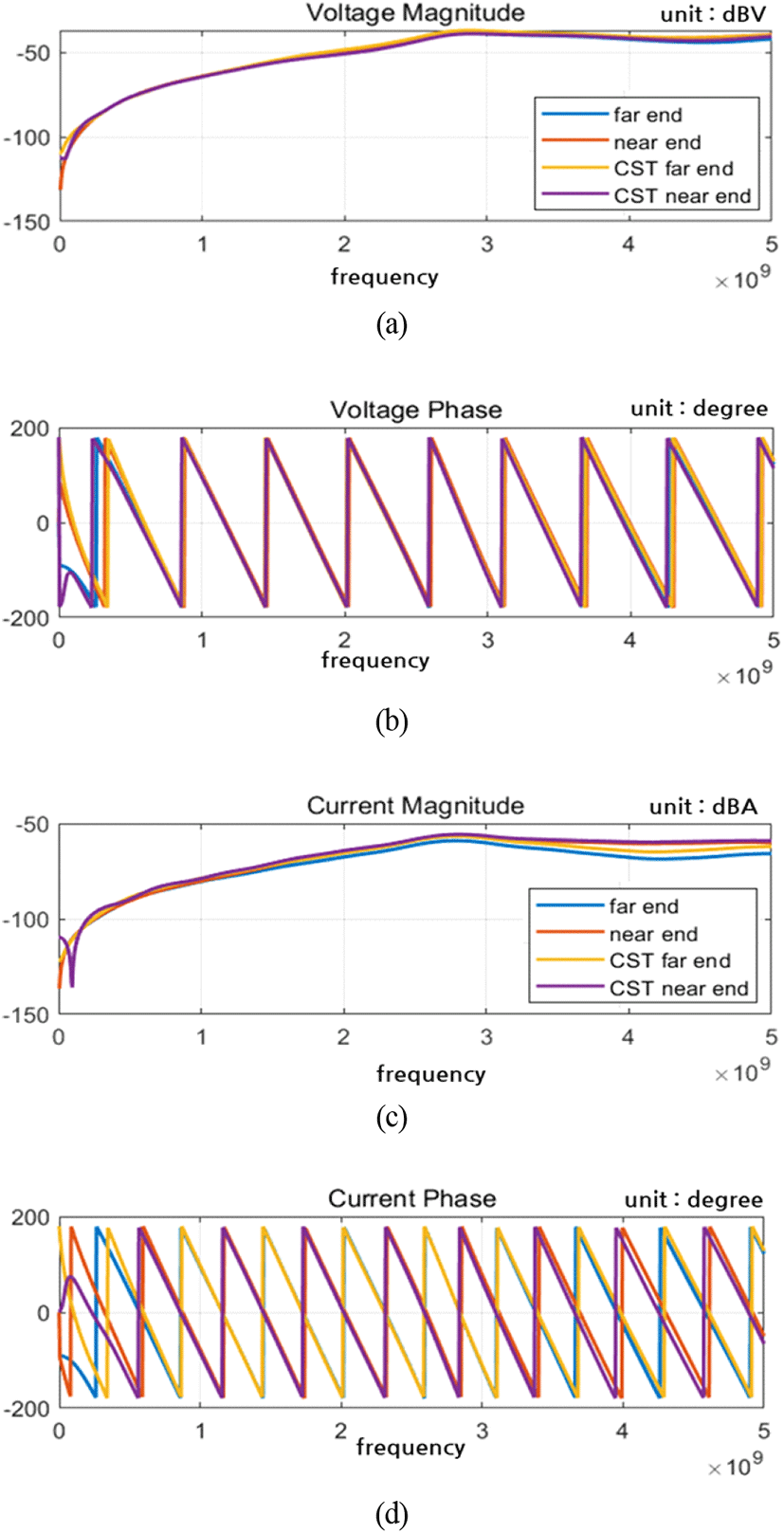
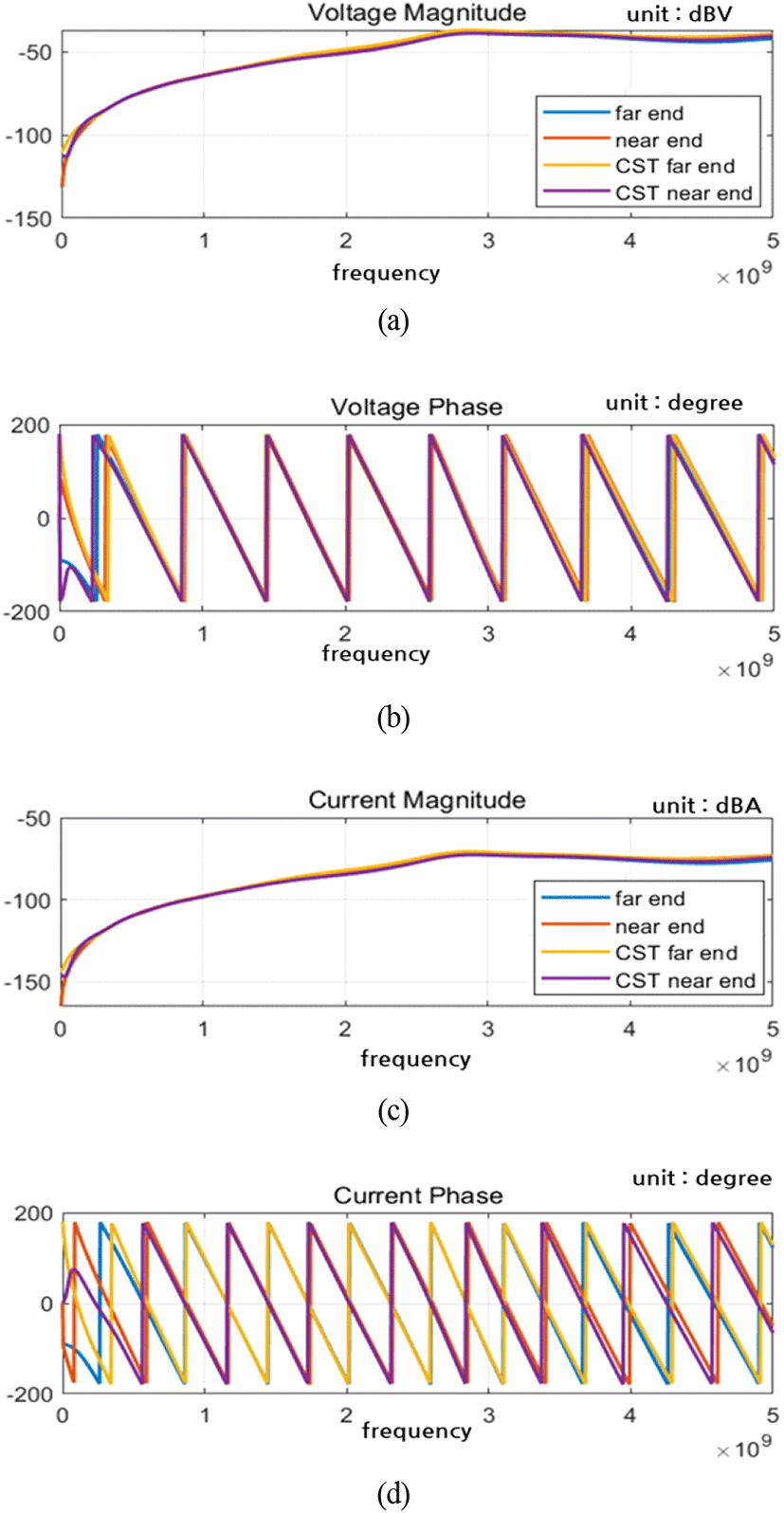
그림 14와 같이 최소 전자기 결합 배치의 경우에는 각 선로가 xy 평면에 수평이다. 이 경우에는 외부 전자기장에 의한 전자기 결합은 전기장의 경우, z축 방향에 영향을 받고, 자기장은 y축 방향에 영향을 받는다.

그림 14. | Fig. 14. 최소 전자기 결합 배치 위치 | Location of least coupled case.

Download Original Figure

그림 15에서 파란색, 빨간색은 본 논문에서 제안한 모델로 계산한 far end, near end 전압, 전류이다. 노란색과 보라색은 각각 CST EM 시뮬레이션을 통해 추출한 데이터이다. 전자기 결합으로 전달되는 최대값은 2.88 GHz에서 전압은 −38.6 dBV, 전류는 −70.7 dBA만큼 전달된다.

그림 15. | Fig. 15. Best case의 양 단에서 제안한 모델과 CST의 (a) 전압 세기, (b) 전압 위상, (c) 전류 세기, (d) 전류 위상 결과 비교 | Comparison of (a) voltage magnitude, (b) voltage phase, (c) current magnitude, (d) current phase results from proposed model and CST of each ends of trace in best case.

Download Original Figure

앞서 기술한 최대 전자기 결합 배치와 최소 전자기 결합 배치의 안테나에서 유기된 노이즈 전압, 전류의 세기를 비교해 보면, 최대 전자기 결합 배치의 경우에는 2.8 GHz에서 −55.7 dBA, −21.7 dBV의 최대 전달을, 최소 전자기 결합 배치의 경우에는 2.88 GHz에서 −70.7 dBA, −36.8 dBV의 최대 전달을 보였다. 동일한 전자기장의 분포를 갖는 조건이라도 선로의 배치 방향에 따라 최대 15 dB까지 크기 차이를 보인다.

또한, 해석시간의 측면에서 보면 Intel Xeon E5-2643 c4 3.40 GHz CPU, 128 GB RAM memory의 PC에서 3 port CST EM simulation의 경우, 142초가 소요되며, 본 논문에서 제안된 모델의 경우 안테나 1-port 및 field probe 포함하여 43초 소요된다. 1-port 시뮬레이션 분석 시, 피해 선로를 제외하고 시뮬레이션을 진행한다. 안테나 대비 크기가 작은 피해선로가 제외되어, 3-port 시뮬레이션 대비 메쉬 개수가 줄어 해석 시간이 단축된다. 이러한 단순한 모델에서도 프로세싱 시간이 3 port 시뮬레이션과 비교해서 70 % 가까이 시간을 단축하여 훨씬 빠르게 분석을 진행할 수 있다.

그 차이는 미비해 보일 수 있으나, 스마트폰과 같이 복잡한 시스템의 적용할 경우 제안한 모델로 분석할 때 시간 절약에 대한 장점이 더 돋보일 것으로 예상한다. 두 번째로, 모델 디버깅, 파라미터 스윕 등 반복적인 계산이 필요한 경우, 그 시간을 훨씬 단축할 수 있다. 마지막으로, 안테나 주변 전자기장 데이터만 있으면, FPCB를 별도로 설계하여도 안테나에 의해 유도되는 노이즈를 예측할 수 있게 되어 설계의 측면에서 상당히 유리하다.

4-3 안테나 근역장 커플링 모델 검증

4-3-1 S-Parameter 비교

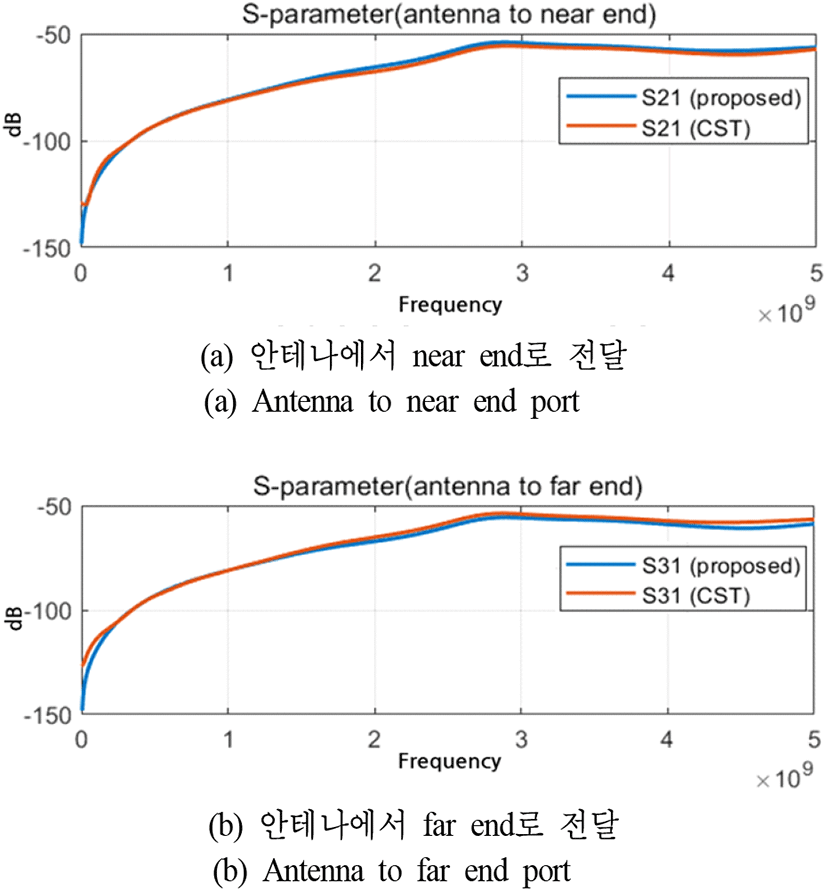
앞서 구한 안테나 근역장에서 인접 전송선로로 유도된 노이즈는 near end, far end의 전압과 전류를 기준으로 확인하였다. 이를 다시 RF에서 가장 많이 쓰이는 S-파라미터로 변환하여 유효성을 확인하였다. 그림 16은 최소 전자기 결합 배치 기준으로 하여 안테나의 급전(port1), near end(port2), far end(port3)로 두고, S₂₁과 S₃₁을 비교한 그래프이다. 결과를 보면, 3-port 3D EM 시뮬레이션인 CST 프로그램으로 추출한 S-파라미터와 본 논문에서 제안한 모델을 기반으로 계산한 값의 정합성이 좋음을 확인할 수 있다. S₂₁과 S₃₁모두 0~5 GHz 전 대역에서 정합성이 좋다. 따라서, 본 논문에서 제안한 모델과 3D EM simulation의 수치해석 결과가 일치함을 확인할 수 있다.

그림 16. | Fig. 16. 최소 전자기 결합 배치의 S-파라미터 결과 | Result of S-parameter in case of least coupled case.

Download Original Figure

Ⅴ. 결 론

본 논문은 인접하게 설계된 안테나와 전송선로 사이에서, 안테나가 전송선로에 얼마만큼의 노이즈를 전달하는지에 대한 분석이다. 수식적인 방법론을 통해, 원역장인 평면파로 제안한 모델에 대한 기존연구와의 정합성을 확인하고, 안테나 근역장으로 확장시켜 분석하였다. PIFA 안테나를 설계하고, 근역장에서 전송선로가 배치되었을 때, 안테나에서 방사되는 신호가 어떻게 선로로 유도되는지 확인하였다. 이를 통해서 전자기 결합으로 전달된 전압, 전류를 예측할 수 있다. 또한, 해당 방법론을 통해서 안테나 근역장 영역에서 피해 선로에 우세한 전기장, 자기장 성분만을 반영하여 모델링을 했으며, 이에 대한 정합성도 수치 해석적인 3D EM 시뮬레이션 결과와 비교하여 유효성을 확인하였다. 이를 바탕으로 하여, 임의의 방향의 전자기장이 인가되어도 본 논문에서 제안한 모델이 유효성이 있음을 확인했다. 또한, 선로의 배치에 따라 같은 조건에서도 전달되는 노이즈의 양이 달라짐을 확인했다. 안테나 근역장 모델에서 선로의 배치만 변경했을 때 15 dB가량의 전달 차이를 보였다. 이뿐만 아니라 제안한 방법론으로 분석하면, 본 논문의 모델의 경우 3D EM 분석 대비 70 %가량 시간이 적게 소모되었다. 스마트폰과 같은 훨씬 더 복잡한 시스템에서 EMI 분석을 더 빠르게 진행할 수 있을 것으로 예상한다. 제안된 방법론을 통해 시스템 설계단계에서 미리 안테나에서 주변부 전송선로에 미치는 전자파 장해를 예측하고, 개선하는 데 도움이 되길 기대한다.

References

[1].

G. Liu, Y. Huang, Z. Chen, L. Liu, Q. Wang, and N. Li, “5G deployment: Standalone vs. non-standalone from the operator perspective,” IEEE Communications Magazine, vol. 58, no. 11, pp. 83-89, Nov. 2020.

[2].

Physical Channels and Modulation(3GPP TS 38.211 Version 15.2.0 Release 15), ETSI TS 138 211 V15.2.0, Jul. 2018.

[3].

Y. Huo, X. Dong, and W. Xu, “5G cellular user equipment: From theory to practical hardware design,” IEEE Access, vol. 5, pp. 13992-14010, Jul. 2017.

[4].

T. H. Lee, C. G. Kim, J. H. Lee, and J. K. Wee, “Analysis of the EMI and SI effects on the flexible-PCBs for mobile application,” in 2008 Electrical Design of Advanced Packaging and Systems Symposium, Seoul, Dec. 2008, pp. 97-100.

[5].

Qualcomm, “Global update on spectrum for 4G & 5G,” 2020. Available: https://www.qualcomm.com/content/dam/qcomm-martech/dm-assets/documents/messaging_presentation_-_4g_5g_spectrums_-_december_2020.pdf

[6].

C. R. Paul, Analysis of Multiconductor Transmission Lines, Hoboken, NJ, John Wiley & Sons, 2007.

[7].

D. Taylor, R. Satterwhite, and C. Harrison, “The response of a terminated two-wire transmission line excited by a nonuniform electromagnetic field,” IEEE Transactions on Antennas and Propagation, vol. 13, no. 6, pp. 987-989, Nov. 1965.

[8].

A. K. Agrawal, H. J. Price, and S. H. Gurbaxani, “Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field,” IEEE Transactions on Electromagnetic Compatibility, vol. EMC-22, no. 2, pp. 119-129, May 1980.

[9].

F. Rachidi, “Formulation of the field-to-transmission line coupling equations in terms of magnetic excitation field,” IEEE Transactions on Electromagnetic Compatibility, vol. 35, no. 3, pp. 404-407, Aug. 1993.

[10].

M. Leone,, H. L. Singer, “On the coupling of an external electromagnetic field to a printed circuit board trace,” IEEE Transactions on Electromagnetic Compatibility, vol. 41, no. 4, pp. 418-424, Nov. 1999.

[11].

S. O. Land, M. Ramdani, R. Perdriau, Y. Braux, and M. Drissi, “Using a modified taylor cell to validate simulation and measurement of field-to-shorted-trace coupling,” IEEE Transactions on Electromagnetic Compatibility, vol. 56, no. 4, pp. 864-870, Aug. 2014.

[12].

S. O. Land, M. Ramdani, and R. Perdriau, “Dominant coupling mechanism for integrated circuit immunity of SOIC packages up to 10 GHz,” IEEE Transactions on Electromagnetic Compatibility, vol. 60, no. 4, pp. 965-970, Aug. 2018.

Author Information

변 성 완 [성균관대학교/석사과정]

jkiees-34-7-451-i1

https://orcid.org/0009-0006-8124-9909
2014년 2월: 성균관대학교 전자전기공학부 (공학사)
2014년 1월~현재: 삼성전자 MX사업부 책임연구원
2022년 3월~현재: 성균관대학교 DMC공학과 석사과정
[주 관심분야] RF, Antenna, EMI/EMC

이 현 재 [성균관대학교/석사과정]

jkiees-34-7-541-i2

https://orcid.org/0009-0002-0798-4172
2022년 2월: 성균관대학교 전자전기공학과 (공학사)
2023년 3월~현재: 성균관대학교 전자전컴퓨터공학과 석사과정
[주 관심분야] SI/PI, EMI/EMC

나 완 수 [성균관대학교/전임교수]

jkiees-34-7-541-i3

https://orcid.org/0000-0002-0315-3294
1884년 2월: 서울대학교 전기공학과 (공학사)
1986년 2월: 서울대학교 전기공학과 (공학석사)
1991년 2월: 서울대학교 전기공학과 (공학박사)
1991년~1993년: SSCL Guest Collaborator
1993년~1995년: 한국전기연구원 선임연구원
1995년~현재: 성균관대학교 전자전기컴퓨터공학과 전임교수
[주 관심분야] SI/PI, EMI/EMC