The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(7):525-533

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.7.525

논문/REGULAR PAPERS

잡음 불확실성이 있는 환경에서 Nakagami-m 페이딩 신호의 스펙트럼 센싱 성능 분석

김창주^†

Performance Analysis of Spectrum Sensing for Nakagami-m Fading Signal Considering Noise Uncertainty

Chang-Joo Kim^†

㈜휴라

Hub of Radio Technology, HURA

^†Corresponding Author: Chang-Joo Kim (e-mail: cjkim@hura.co.kr)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 03, 2023; Revised: Jul 17, 2023; Accepted: Jul 18, 2023

Published Online: Jul 31, 2023

요 약

스펙트럼 센싱(spectrum sensing) 기술은 주파수를 공동으로 사용하는 대역에서 매우 중요한 역할을 한다. 그러나 배경 잡음이 시간과 장소에 따라 균질하지 않기 때문에 전통적으로 사용되어온 에너지 검파기를 사용하면 스펙트럼의 센싱 확률이 낮아진다. 이를 보완하기 위해 순서 통계(order statistics) 검파기를 사용하는데, 이는 균질하지 않은 배경 잡음에 대한 내재적인 보호 기능을 가지고 있다. 그런데 잡음 불확실성이 있는 환경에서 Nakagami-m 페이딩 신호의 스펙트럼 센싱의 성능을 분석한 연구는 아직까지 이루어지지 않았다. 본 논문에서는 Nakagami-m 페이딩 신호의 스펙트럼 센싱 성능을 분석하고, 잡음 불확실성이 있는 환경에서 강건하게 스펙트럼 센싱을 하는 GOS-L-m 검파기를 제안한다. 오 경보 확률의 식을 유도하고, 이 식으로부터 일정한 오 경보율을 유지하기 위한 임계값(threshold)을 산출하여, 이를 토대로 잡음 불확실성이 있는 환경에서 GOS-L-m 검파기의 검파 확률을 얻는다. 분석 결과, GOS-L-m 센싱 방식은 GOS-L-m 검파기의 계수를 올바르게 선택하면 강건한 검파 성능을 달성할 뿐만 아니라, 원하는 오 경보율(constant false alarm rate)을 얻을 수 있음을 알 수 있다.

Abstract

Spectrum sensing is of significance in shared spectrum bands. Traditional energy detectors are limited by the variance in background noise, which can reduce the sensing probability. Order statistics detectors, which are inherently protected against non-uniform background noise, can complement energy detectors. However, to date, the spectrum sensing performance of Nakagami-m fading signals has not been analyzed. In this paper, we fill this gap by analyzing the spectrum sensing performance of Nakagami-m fading signals and proposing a robust sensing method called the GOS-L-m detector for noise-uncertain environments. We derive the false alarm probability formula for the GOS-L-m detector, and calculate a threshold value to maintain a constant false alarm rate. Based on this, we obtain the detection probability in a noise-uncertain environment. Our analysis shows that the GOS-L-m sensing method achieves robust detection performance and maintains the desired constant false alarm rate if the coefficients of the GOS-L-m detector are correctly selected.

Keywords: Nakagami-m Fading; GOS Detector; Spectrum Sensing; Noise Uncertainty

Ⅰ. 서 론

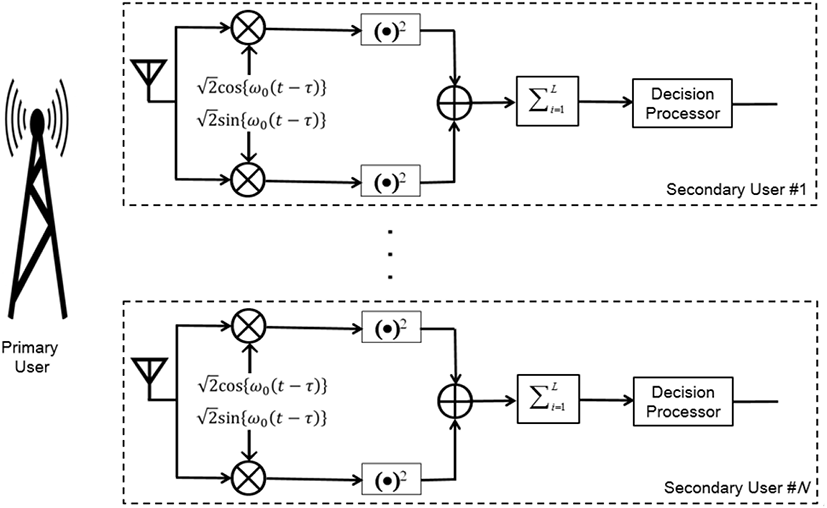
무선 기술이 발전함에 따라 전파자원의 수요는 계속 증가하는 데 비하여 가용한 스펙트럼 자원은 한정되어 있어 주파수 부족이 점차 심화되고 있다. 이와 같이 전파자원이 부족한데도 불구하고, 지역적으로 또는 시간적으로 사용되지 않는 스펙트럼이 많이 있다. 인지 무선(cognitive radio) 기술은 스펙트럼 센싱을 통해 채널의 사용 여부를 인지할 수 있다. 이를 토대로 1차 사용자가 해당 채널을 사용하는지를 판단하고, 사용하지 않으면 해당 주파수를 2차 서비스로 사용함으로써 주파수 이용 효율을 높여준다^[1]~[4]. 그림 1은 PU(primary user)와 SU(secondary user) 간의 주파수 공동사용을 위한 검파기의 구조이다^[5]. 인지 무선 장치가 사용하는 동작 채널(operating channel)에 PU가 나타나면 SU는 PU를 즉시 인지하고 백업 채널(backup channel)로 채널 이동 시간(channel move time) 내에 이동하거나 서비스를 중단해야 한다. 이러한 스펙트럼 공동사용(spectrum sharing) 방식은 스펙트럼의 최적화된 사용을 가능하게 하면서 PU에 대한 간섭을 최소로 줄일 수 있다. 따라서 PU와 SU 간의 공존(co-existence)을 보장하기 위해서는 PU 신호를 정확하게 인지해야 한다.

그림 1. | Fig. 1. 주파수 공동사용을 위한 GOS-L-m 검파기 구조 | Structure of the GOS-L-m detector for spectrum sharing.

Download Original Figure

무선통신의 채널 모델로는 LOS(line of sight) 환경부터 레일리 페이딩(Rayleigh fading) 환경에 이르기까지 다양한 페이딩 환경을 모델링하는 Nakagami-m 페이딩 모델을 사용한다^[6]~[10]. 일반적으로 SU는 PU 신호에 대한 사전 지식이 필요하지 않은 ED(energy detector)를 주로 사용한다^[11]~[16]. 에너지 검출은 잡음 불확실성이 없을 때는 검파 성능이 좋으나, 다중경로 성분, 간섭, 다른 대역의 누설 신호 등이 수신 신호에 포함되면 성능이 급격하게 떨어진다^[12]. 따라서 ED는 잡음 불확실성이 있는 환경에서는 원하는 검파 성능을 보장할 수 없을 뿐만 아니라, 오 경보율도 일정하게 유지할 수 없는 단점이 있다. 이에 반하여 순서 통계 검파기는 균일하지 않은 환경에서도 강건한 검파특성을 유지한다고 알려져 있다^[17]~[24]. 그러나 잡음 불확실성이 있는 환경에서 Nakagami-m 페이딩 신호를 OS(order statistics) 검파기를 이용하여 검파성능을 분석한 연구는 아직까지 이루어지지 않았다. OS 검파기를 스펙트럼 센싱에 적용한 논문은 몇 개 정도이다. 참고문헌 [23]은 배경 잡음 레벨을 추정하기 위해 중앙값 추정 기(M-estimator)를 제안했으며, M-estimator는 일부 간섭 상황에서 오 경보율의 강건성(robustness)을 보였다. 참고문헌 [24]에서 Rostami 등은 OS 기반 스펙트럼 센싱을 제안했지만, 그들의 분석은 AWGN 채널로 제한되었으며, Monte Carlo 시뮬레이션을 통해 검출 및 오 경보 성능을 얻었다. 최근에 Rayleigh 페이딩 신호에 대한 GOS(generalized order statistics) 검출기의 검파 및 오 경보율에 대한 성능이 분석되었다^[5]. 본 논문에서는 강건한 스펙트럼 센싱 구조인 GOS 검출기를 활용하여 Nakagami-m 페이딩 신호의 오 경보 및 검출 확률에 대한 수식을 유도하고, 성능을 분석한다.

Ⅱ. 검파기 모델

무선통신에서는 PU 신호가 장애물 등에 가려져 있거나, 다중경로 페이딩(fading)이 심한 채널 환경이 자주 발생한다. 이러한 환경에서 PU와 SU 간의 공존을 보장하기 위해서는 SU는 PU의 매우 약한 신호까지도 감지하여야 한다. 또한 배경 잡음은 열잡음은 물론 다중경로 성분, 주변 시스템으로부터의 간섭, 그리고 인접 대역의 누설 신호 등 다양한 원인으로 생길 수 있다. 따라서 잡음 불확실성에 강인한 스펙트럼 센싱 기술을 개발하는 것이 필요하다.

그림 1에 도시한 스펙트럼 센싱 방식은 I-채널과 Q-채널 신호를 제곱하여 더하는 제곱법 검파기(square-law detector)를 기본으로 한다. 제곱법 검출기의 출력은 L개씩 더하여 비동기적 통합(noncoherent integration)을 한 후에 그림 2에 도시한 결정 프로세서로 입력된다. 이러한 배경 잡음 레벨은 그림 2에 도시한 기준 윈도우(reference window)에 FIFO(first in first out) 방식으로 저장된다. 그리고 배경 레벨의 추정값은 데이터 샘플 수인 M개의 데이터 X₁, X₂, ···, X_M의 함수로 추정한다. 평균 레벨(mean level) 추정기에서의 추정값은 $X = ∑ i = 1 M X i$ 와 같이 모든 셀을 합산하여 배경 레벨의 잡음을 얻는다. 순서 통계 방식에서는 그림 2의 기준 윈도우에서의 데이터 샘플을 오름차순으로 정렬하여 크기가 가장 작은 값부터 크기가 큰 순서로 정렬한다. 즉, X₍₁₎≤X₍₂₎≤…≤X_(M)이 되며, 여기서 X₍₁₎은 가장 작은 값이고 X_(M)은 가장 큰 값이다. k번째 순서 통계 추정기는 X=X_(k)로 표시된다. 시험(test) 셀(cell) Y는 TX와 비교되며, T는 원하는 오 경보율(CFAR)을 달성하기 위해 사용되는 스케일링 인자(scaling factor)이다. Kim 등은 균질하지 않은 환경에서 레이다 신호를 강건하게 검출하기 위해 일반화된 순서 통계 검출기를 유도했으며, 이를 GOS CFAR detector, 즉 오 경보율이 일정한 일반화된 순서통계 검파기라고 명명하였다^[19],[20]. GOS 검파기에서 배경 레벨에 대한 추정값은 $X = f (X (1), …, X (M)) = ∑ i = 1 M α i X (i)$ 이다. 여기에서 α_i는 1 또는 0의 값을 갖는다. 또한 GOS CFAR 검파기를 다중 경로 페이딩이 있는 모바일 채널에 적용하여 PN(pseudo noise) 시퀀스를 검파하는 데 적용하였다^[21],[22].

그림 2. | Fig. 2. GOS-L-m 검파기의 결정 프로세서 내부의 가설 검증 시험 구조 | Hypothesis testing scheme of decision processor for GOS-L-m detector.

Download Original Figure

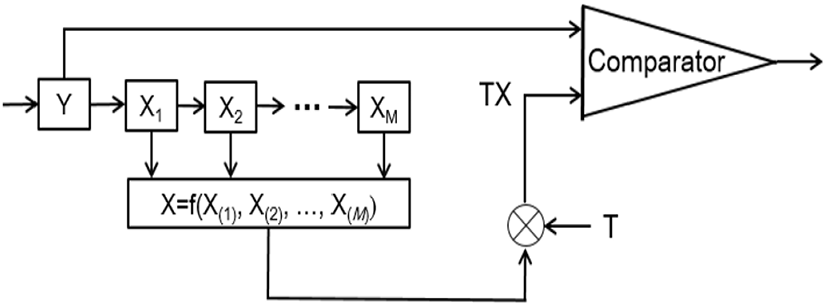
본 논문에서는 잡음 불확실성이 있는 환경에서 Nakagami-m 페이딩 신호에 대하여 강건한 검파 특성을 갖는 GOS-L-m을 제안하고, 오 경보 확률의 검파 확률에 대한 수식을 유도한다. GOS-L-m 검파기에서 L은 적분 개수이고, m은 Nakagami-m 페이딩 파라미터이다.

III. GOS-L-m 검파기의 해석

3-1 GOS-L-m 검파기의 수학적 해석

PU 검파는 로컬 결정 프로세서에 있는 시험 셀 Y의 값이 임계값 TX보다 크면 PU가 존재한다고 선언한다.

H 1 > Y T X H 0 <

(1)

여기에서 대립가설(alternative hypothesis) H₁은 PU 신호가 있음을 의미하고, 귀무 가설(null hypothesis) H₀은 PU 신호가 없음을 의미한다. 그림 2에서 비동기적으로 통합(noncoherent integration)된 신호 Y는 식 (2) 및 식 (3)과 같이 모델링된다^[11]~[13].

p 0 (y) = y L − 1 e − y Γ (L)

(2)

p 1 (y) = 1 Γ (m L) (m S ¯) m L y m L − a e − m y / S ¯, y ≥ 0

(3)

여기서 $S ¯$ 는 평균 신호대잡음비이고 m은 Nakagami 페이딩 인자이다. MGF(moment generating function)와 등고선 적분법(contour integration)을 모두 사용하여, 검파 확률과 오 경보 확률을 식 (4) 및 식 (5)와 같이 얻을 수 있다^[25].

p f a = − ∑ k 0 r e s [M 0 (s) M X (− T s) s, s k 0]

(4)

p d = − ∑ k 1 r e s [M 1 (s) M X (− T s) s, s k 1]

(5)

여기서 M_j(_s) (j=0, 1)는 p_j(y)에 대한 MGF이다. 그리고 $s k 0$ 와 $s k 1$ 는 각각 M_0(s)와 M_1(s)의 좌측 절반 평면에 있는 극점(left half-plane poles)이다. M_X(−Ts)는 확률 밀도 함수의 MGF에서 s를 −Ts로 대체하여 구할 수 있다. 그리고 res[·]는 residue를 표시한다. 식 (2) 및 식 (3)의 MGF는 간단하게 식 (6) 및 식 (7)과 같이 구할 수 있다.

M 0 (s) = 1 (1 + s) L

(6)

M 1 (s) = 1 (1 + S ¯ m s) m L, m ≥ 12

(7)

그러나 수신된 데이터 샘플에 잡음은 물론 간섭 신호 등의 잡음 불확실성이 포함되어 있다면 이 같은 비균질적 환경에서의 비동기적 통합(noncoherent integration)은 식(8)로 표현된다^{[19],[20],[23],[26]}.

p (x i) = x i L − 1 e − x i / (1 + I ¯ i) (L − 1) −! (1 + I ¯ i) L, 1 ≤ i ≤ M

(8)

여기서 Ī_i는 기준 윈도우에 있는 각 셀의 평균 INR (interference-to-noise ratio), 즉 평균 간섭 신호 대 잡음의 비율이다. 만일 열잡음만 존재하는 경우에는 Ī_i=0이다.

GOS 검파기의 로컬 결정 프로세서에 사용되는 배경 레벨 추정값 $X = ∑ i = 1 M α i X (i)$ 의 MGF는 식 (9)와 같이 구할 수 있다.

M X (s) = E X (E x p (− s X)) = E X (E x p (− s ∑ i = 1 M α i X (i))) = ∑ A l l M! I n v e r s e s ∫ 0 ∞ d x (1) x (1) L − 1 [E x p (− x (1) β (1))] Γ (L) β (1) × … × ∫ x (M − 1) ∞ d x (M) x (M) L − 1 [E x p (− x (M) β (M))] Γ (L) β (M) E x p (− s ∑ i = 1 M α i x (i)) = ∑ A l l M! I n v e r s e s ∑ p M = 0 L − 1 ∑ p M − 1 = 0 L − 1 + p M … ∑ p 2 = 0 L − 1 + p 3 ∏ i = 1 M (L + p i − 1 L − 1) β (i) L × (∑ j = i M (β (j) − 1 + s α j)) − (L + p i + 1 − p i)

(9)

여기서 β_(i)=1+I_(i)이고, β_(i)는 그림 2에 있는 배경 레벨 추정기의 데이터 샘플을 크기순으로 분류(sorting)한 후에 얻어지는 i-번째 최소값의 INR이다. 그리고 All M! Inverses는 {X₁, X₂, …, X_M}과 {X₍₁₎, X₍₂₎, …, X_(M)} 사이에 존재하는 모든 경우의 수를 나타낸다^[26].

식 (6)의 MGF는 s=−1에서 차수가 L인 극점(pole)을 갖기 때문에 GOS-L-m 검파기의 오 경보율은 식(6) 및 식 (9)를 식 (4)에 대입하면 식 (10)을 얻을 수 있다.

p f a = ∑ A l l M! I n v e r s e s ∑ p M = 0 L − 1 ∑ p M − 1 = 0 L − 1 + p M … ∑ p 2 = 0 L − 1 + p 3 ∑ q 1 = 0 L − 1 ∑ q 2 = 0 q 1 … ∑ q M − T 2 = 0 q M − T 2 − 1 ∏ i = 1 M (L + p i + 1 − p i + q i − q i + 1 − 1 L + p i + 1 − p i − 1) (L + p i − 1 L − 1) β (i) L × ((T ∑ j = i M α j) q i − q i + 1 (∑ j = i M (β (j) − 1 + T α j)) L + p i + 1 − p i + q i − q i + 1)

(10)

여기서 T₂는 기준 창(reference window)에 크기순으로 정렬된 셀에서 상위 끝에서 제거될 샘플 수이다. 만일 L 이 1이면 식 (10)은 식 (11)로 간략화된다.

p f a = ∑ A l l M! I n v e r s e s ∏ i = 1 M β (i) − 1 [∑ j = i M (β (j) − 1 + T α j)] − 1

(11)

뿐만 아니라 잡음 불확실성이 없다면 식 (11)은 식 (12)로 더욱 간단하게 표현된다.

p f a = ∏ i = 1 M M − i + 1 M − i + 1 + T ∑ j = i M α j

(12)

한편, 식 (7)의 MGF는 $s = − m / S ¯$ 에서 차수가 mL인 폴을 갖기 때문에 검파 확률에 관한 식은 식 (7) 및 식 (9)를 식 (5)에 대입하면 식 (13)을 얻을 수 있다.

p d = ∑ A l l M! I n v e r s e s ∑ p M = 0 L − 1 ∑ p M − 1 = 0 L − 1 + p M … ∑ p 2 = 0 L − 1 + p 3 ∑ q 1 = 0 m L − 1 ∑ q 2 = 0 q 1 … ∑ q M − T 2 = 0 q M − T 2 − 1 ∏ i = 1 M (L + p i + 1 − p i + q i − q i + 1 − 1 L + p i + 1 − p i − 1) (L + p i − 1 L − 1) β (i) L × ((m T S ¯ × ∑ j = i M α j) q i − q i + 1 (∑ j = i M (β (j) − 1 + m T α j S ¯)) L + p i + 1 − p i + q i − q i + 1)

(13)

이상 유도된 식을 토대로 성능을 분석하기 위하여 식 (13)에서의 m값은 정수를 가정하고, GOS-L-m 검파기의 데이터 샘플 수(M)는 8로 가정한다. 표 1은 GOS 알고리즘의 다양한 형태에 따라 원하는 오 경보율(FAR)을 얻기 위한 임계 계수 T의 값이다. 표 1은 식 (12)로부터 얻는다. GOS(1, 2, …,6) 검파기는 배경 레벨의 추정치를 얻기 위해 일곱 번째로 작은 샘플과 여덟 번째 작은 샘플이 제외되고, GOS(1, 2, …,8) 검파기는 그림 2의 창에 있는 모든 샘플에 대한 배경 전력 레벨의 합으로 정의된다. 따라서 GOS(1, 2, …,8) 검파기는 ML(mean level) 검파기와 성능이 동일하다. 또한 표 1로부터 L이 동일한 경우 원하는 CFAR값이 감소함에 따라 임계 계수 T의 값은 증가함을 알 수 있다.

표 1. | Table 1. M=8인 경우의 GOS-L 검파기의 임계 계수 T | Threshold coefficient T of GOS-L detector (M=8).

Environments of decision processor	L	P_fa=10⁻²	P_fa=10⁻³	P_fa=10⁻⁴
GOS(1,2,…,8) or ML α=(1,1,1,1,1,1,1,1)	1	0.778	1.371	2.162
GOS(1,2,…,8) or ML α=(1,1,1,1,1,1,1,1)	2	0.496	0.752	1.042
GOS(1,2,…,7) α=(1,1,1,1,1,1,1,0)	1	1.242	2.250	3.654
GOS(1,2,…,7) α=(1,1,1,1,1,1,1,0)	2	0.700	1.068	1.498
GOS(1,2,…,6) α=(1,1,1,1,1,1,0,0)	1	1.976	3.721	6.291
GOS(1,2,…,6) α=(1,1,1,1,1,1,0,0)	2	0.981	1.526	2.174

Download Excel Table

3-2 GOS-L-m 검파기 성능 분석

GOS-L-m 검출기의 성능을 분석하기 위하여 먼저 L=1이고, 균질 환경(homogeneous environments)인 경우를 살펴보자. 그림 3은 다른 Nakagami-m 페이딩의 매개 변수 m에 따라 GOS(1, 2, …,8)-1-m 검파기의 검파 확률을 나타낸다. 그림에서 P_d>0.3인 영역에서는 GOS(1, 2, …,8)-1-3 검파기가 세 가지 유형의 GOS 검파기 중에서 가장 우수한 성능을 보여준다. 이는 매개 변수 m의 값이 커짐에 따라 Nakagami-m 페이딩의 정도가 감소하기 때문이다. 따라서 GOS(1, 2, …,8)-1-1 검파기가 가장 낮은 성능을 보인다. 반면에 P_d<0.3인 경우 Rayleigh 페이딩 채널의 무작위성(randomness)이 검출 성능을 높이므로 GOS(1, 2, …,8)-1-1 검출기가 다른 검출기보다 우수한 성능을 보인다. 성능 비교를 일관되게 유지하기 위하여 모든 그래프에서 P_fa=10⁻³의 CFAR에 해당되는 scaling factor T를 사용한다.

그림 3. | Fig. 3. 잡음 불확실성이 없는 환경에서 GOS(1, 2, …,8)-1-m 검파기의 검파확률(M=8) | Detection probabilities of GOS(1, 2, …,8)-1-m detectors in no noise uncertainty (M=8).

Download Original Figure

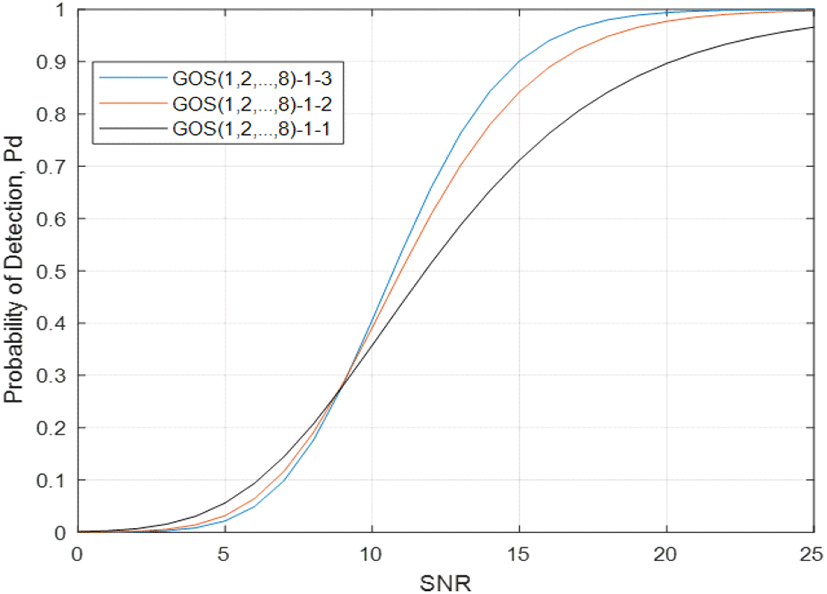
그림 4는 균질 환경(homogeneous environments)에서 전력 레벨을 추정하는 샘플의 수 M이 8에서 7로 줄어든 경우, 즉 GOS(1, 2, …,7)-1-m 검파기의 검파 확률을 나타낸다. 그림에서 볼 수 있듯이 GOS(1, 2, …,7)-1-m 검파기의 성능은 그림 3에 도시한 GOS(1, 2, …,8)-1-m 검파기보다 검파 성능이 떨어지는 것을 알 수 있다. 이는 GOS(1, 2, …,7)-1-m 검파기의 전력 레벨 추정에서는 X₍₈₎이 제거되기 때문에 GOS(1, 2, …,8)-1-m 검파기와 비교하여 실질적으로 M이 8에서 7로 감소하는 효과를 주기 때문이다. Nakagami-m 페이딩 채널의 매개 변수인 m의 영향은 GOS(1, 2, …,8)-1-m 검출기와 유사한 경향을 나타낸다.

그림 4. | Fig. 4. 잡음 불확실성이 없는 환경에서 GOS(1, 2, …,7)-1-m 검파기의 검파확률(M=8) | Detection probabilities of GOS(1, 2, …,7)-1-m detectors in no noise uncertainty (M=8).

Download Original Figure

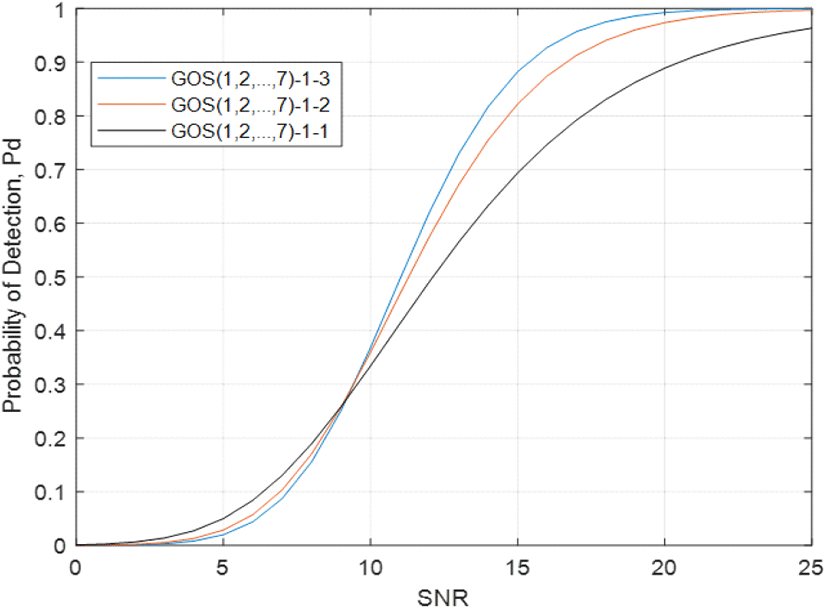
그림 5는 균질 환경에서 매개 변수가 다른 L과 m을 가진 GOS(1, 2, …,8)-L-m 검파기의 검파 확률을 보여준다. 그림에서 볼 수 있듯이 GOS(1, 2, …,8)-2-m 검파기의 성능은 GOS(1, 2, …,8)-1-m 검파기보다 우수한 검파 성능을 보인다. 이는 GOS(1, 2, …,8)-2-m 검파기의 배경 레벨 추정기의 수가 GOS(1, 2, …,8)-1 검파기의 배경 레벨 추정기의 수보다 두 배 많기 때문이다. 이러한 점을 토대로 우리는 P_d>0.3의 영역에서 GOS(1,2,…,8)-L-3 검출기의 성능이 GOS(1,2 …,8)-L-2 검파기 또는 GOS(1,2,…,8)-L-1 검파기보다 우수한 성능을 나타낼 것으로 예측할 수 있다. 따라서 검출 성능은 채널 특성인 m과 통합 샘플 수(L)에 따라 달라진다.

그림 5. | Fig. 5. L과 m의 여러 조합에 따른 GOS-L-m 검파 확률 | Detection probabilities of GOS-L-m detector with different L and m.

Download Original Figure

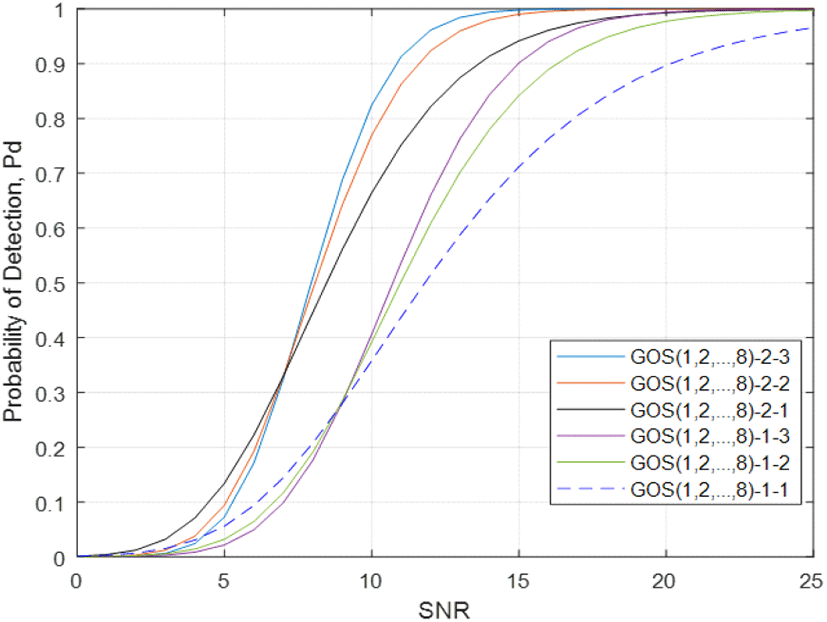
그러면 그림 2의 기준 창(reference window)에 열잡음과 다른 분포를 가진 두 종류의 비균질 간섭 신호가 포함되어 있다고 가정해 보자. 낮은 SINR 환경에서 GOS-L-m 검파기의 성능을 보여주기 위해 간섭 신호의 전력 수준이 PU 신호와 동일하다고 가정한다. 이 경우 GOS(1, 2, …,8) 검파기의 배경 레벨 추정에는 두 개의 간섭 신호가 포함된다. 그림 6에서는 이러한 유형의 잡음 불확실성이 있는 비균질 환경(nonhomogeneous environments)에서 GOS(1, 2, …,8)-2-2 검파기와 GOS(1, 2, …,8)-1-1 검파기의 검파 성능이 모두 심각하게 저하되는 것을 볼 수 있다. 네 개의 검파기 중에서 GOS(1, 2, …,8)-1-1 검파기의 검파성능이 가장 나쁜 것을 볼 수 있다. 반면에 GOS(1, 2, …,6) 검파기는 배경 전력 레벨의 추정 과정에서 간섭 신호를 제외하기 때문에 검파 성능을 잘 유지한다. 특히 GOS(1, 2, …,6)-2-2 검파기는 잡음 불확실성 환경에서도 매우 우수한 검파 성능을 보인다.

그림 6. | Fig. 6. 잡음 불확실성 환경에서 다양한 유형의 GOS 검파기의 검파 확률(M=8, 간섭 신호 수=2, SIR=1) | Detection probabilities of several types of GOS detectors in noise uncertainty environments (M=8, No. of interferers=2, SIR=1).

Download Original Figure

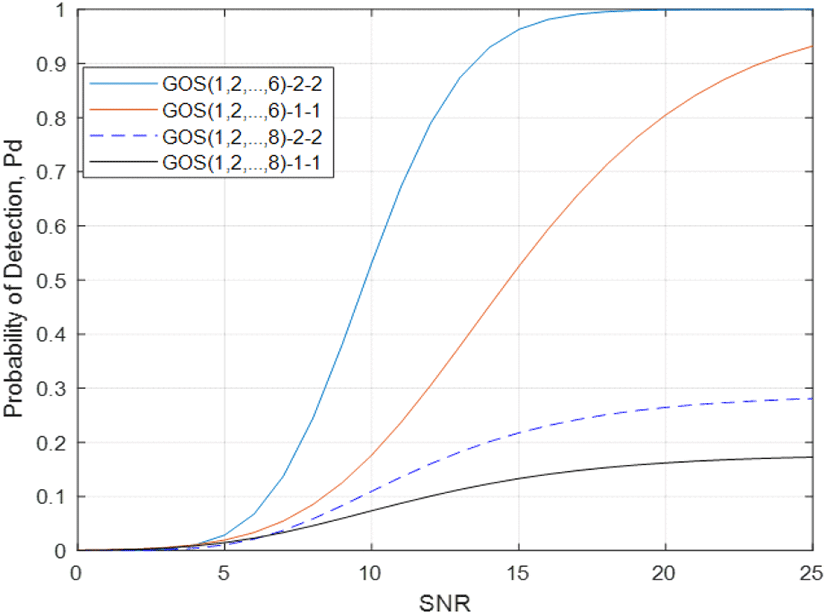
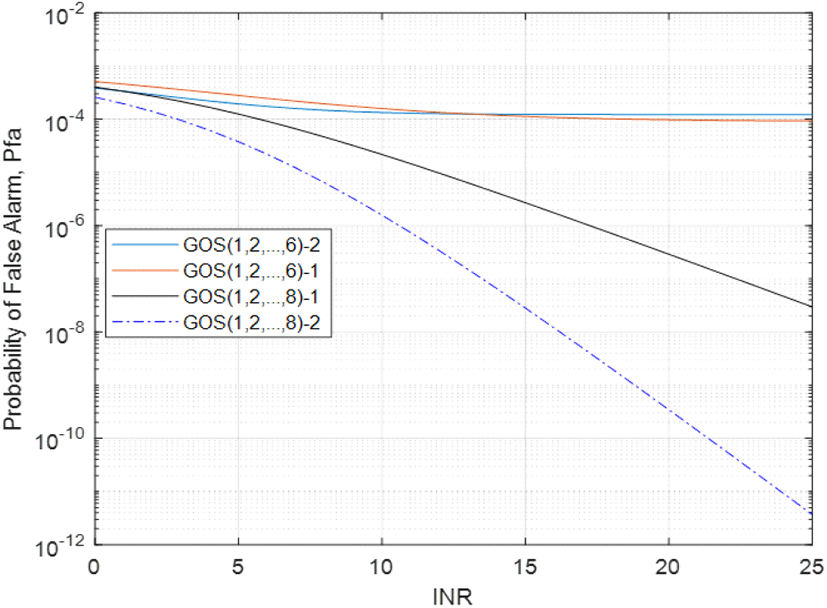
그림 7은 그림 6과 동일한 상황에서 GOS-L-m 검파기가 설계된 오 경보율을 잘 유지하는지를 알아보기 위한 그래프이다. 그림 7에서 GOS(1, 2, …,6) 검파기는 원하는 FAR을 상대적으로 잘 유지하는 것을 볼 수 있다. 반면, GOS(1, 2, …,8) 검파기의 오 경보율은 INR의 증가에 따라 크게 감소한다. 이는 그림 6에서 나타난 것처럼 GOS(1, 2, …,8) 검파기의 threshold가 증가하는 요인이 되고, 그 결과로 검파 성능이 나빠지게 된다. 즉, 이러한 유형의 잡음 불확실성이 있는 환경에서는 GOS(1, 2, …,8) 검파기의 PU 검파 확률이 매우 낮아짐을 의미한다.

그림 7. | Fig. 7. 잡음 불확실성이 있는 비 균질 환경에서 다양한 유형의 GOS 검파기의 오 경보확률(M=8, 간섭 신호 수=2) | False alarm probabilities of several types of GOS detectors in nonhomogeneous environments with noise uncertainty (M=8, No. of interferers=2).

Download Original Figure

잡음 불확실성이 있는 환경에서는 배경 레벨의 추정 과정에서 간섭 신호를 제거하는 것이 매우 중요하다. GOS-L-m 구조는 GOS-L-m 검출기의 계수 α_i를 적절히 선택하여 잡음 불확실성이 있는 환경에서 강건한 검파 성능을 달성하고 원하는 오 경보율을 유지할 수 있다.

Ⅳ. 결 론

에너지 검파기는 균질 환경에서는 성능이 우수하지만, 잡음 불확실성이 있는 비균질 환경에서는 성능이 매우 떨어진다. OS 검출기는 비균질 전파 환경에서 내재적인 보호 기능을 제공하지만, 아직 OS 검출기를 스펙트럼 센싱에 적용하는 연구는 몇몇 연구에 그치고 있다. 본 논문에서는 일반화된 순서 통계 검파기에 Nakagami-m 페이딩 신호가 수신되는 경우에 대한 검파 및 오 경보 확률의 식을 유도하고, 결과를 분석하였다. 분석 결과 분석 결과 잡음 불확실성이 없을 때 배경 레벨을 추정하는 기준 윈도우에서 누적된(noncoherent integration) 데이터의 샘플 수가 증가함에 따라 검출 성능이 향상됨을 보여준다. 잡음 불확실성이 있는 환경에서는 배경 레벨의 추정 과정에서 간섭 신호를 제거하는 것이 매우 중요하다. GOS-L-m 구조는 GOS-L-m 검출기의 계수 α_i를 적절히 선택하여 잡음 불확실성이 있는 환경에서 강건한 검파 성능을 달성하고 원하는 오 경보율을 유지할 수 있다.

Acknowledgements

본 연구는 중소기업 기술개발 지원사업[고경력연구인력 채용]의 일환으로 수행하였음.

References

[1].

C. J. Kim, “Analysis of radio spectrum policy for the creative usage of radio waves,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 25, no. 8, pp. 828-837, Aug. 2014.

[2].

H. S. Bae, Y. S. Kim, C. H. Lim, C. J. Kim, and Y. S. Cho, “Spectrum sensing technique for OFDM signals,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 32, no. 1, pp. 35-41, Jan. 2021.

[3].

Y. C. Liang, K. C. Chen, G. Y. Li, and P. Mahonen, “Cognitive radio networking and communications: An overview,” IEEE Transactions on Vehicular Technology, vol. 60, no. 7, pp. 3386-3407, Sep. 2011.

[4].

T. Yucek, H. Arslan, “A survey of spectrum sensing algorithms for cognitive radio applications,” IEEE Communications Surveys & Tutorials, vol. 11, no. 1, pp. 116-130, Mar. 2009.

[5].

C. J. Kim, E. S. Jin, K. Cheon, and S. H. Kim, “Robust spectrum sensing under noise uncertainty for spectrum sharing,” ETRI Journal, vol. 41, no. 2, pp. 176-183, Apr. 2019.

[6].

M. Nakagami, “The m-distribution: A general formula of intensity distribution of rapid fading,” in Proceedings of a Symposium Held at the University of California, Los Angeles, CA, Jun. 1958, pp. 3-6.

[7].

P. Lombardo, G. Fedele, and M. M. Rao, “MRC performance for binary signals in Nakagami fading with general branch correlation,” IEEE Transactions on Communications, vol. 47, no. 1, pp. 44-52, Jan. 1999.

[8].

G. K. Karagiannidis, D. A. Zogas, and S. A. Kotsopoulos, “On the multivariate Nakagami-m distribution with exponential correlation,” IEEE Transactions on Communications, vol. 51, no. 8, pp. 1240-1244, Aug. 2003.

[9].

P. Dharmawansa, N. Rajatheva, and K. Ahmed, “On the distribution of the sum of Nakagami-m random variables,” IEEE Transactions on Communications, vol. 55, no. 7, pp. 1407-1416, Jul. 2007.

[10].

V. A. Aalo, “Performance of maximal-ratio diversity systems in a correlated Nakagami-fading environment,” IEEE Transactions on Communications, vol. 43, no. 8, pp. 2360-2369, Aug. 1995.

[11].

V. I. Kostylev, “Energy detection of a signal with random amplitude,” in 2002 IEEE International Conference on Communications. Conference Proceedings. ICC 2002, New York, NY, Apr.-May 2002, pp. 1606-1610.

[12].

F. F. Digham, M. S. Alouini, and M. K. Simon, “On the energy detection of unknown signals over fading channels,” IEEE TTransactions on Communications, vol. 55, no. 1, pp. 21-24, Jan. 2007.

[13].

S. P. Herath, N. Rajatheva, and C. Tellambura, “Energy detection of unknown signals in fading and diversity reception,” IEEE Transactions on Communications, vol. 59, no. 9, pp. 2443-2453, Sep. 2011.

[14].

R. Tandra, A. Sahai, “SNR walls for signal detection,” IEEE Journal of Selected Topics in Signal Processing, vol. 2, no. 1, pp. 4-17, Feb. 2008.

[15].

D. M. Martínez, A. Andrade, “Reducing the effects of the noise uncertainty in energy detectors for cognitive radio networks,” International Journal of Communication Systems, vol. 30, no. 1, p. e2907, Dec. 2017.

[16].

S. Nallagonda, S. D. Roy, S. Kundu, G. Ferrari, and R. Raheli, “Censoring-based cooperative spectrum sensing with improved energy detectors and multiple antennas in fading channels,” IEEE Transactions on Aerospace and Electronic Systems, vol. 54, no. 2, pp. 537-553, Apr. 2018.

[17].

H. Rohling, “Radar CFAR thresholding in clutter and multiple target situations,” IEEE Transactions on Aerospace and Electronic Systems, vol. AES-19, no. 4, pp. 608-621, Jul. 1983.

[18].

N. Levanon, “Detection loss due to interfering targets in ordered statistics CFAR,” IEEE Transactions on Aerospace and Electronic Systems, vol. 24, no. 6, pp. 678-681, Nov. 1988.

[19].

C. J. Kim, D. S. Han, and H. S. Lee, “Generalized OS CFAR detector with noncoherent integration,” Signal Processing, vol. 31, no. 1, pp. 43-56, Mar. 1993.

[20].

C. J. Kim, H. S. Lee, “Analysis of the generalized order statistics constant false alarm detector,” ETRI Journal, vol. 16, no. 1, pp. 17-34, Apr. 1994.

[21].

C. J. Kim, H. S. Lee, and H. J. Lee, “Adaptive acquisition of PN sequences for DSSS communications,” IEEE Transactions on Communications, vol. 46, no. 8, pp. 993-996, Aug. 1998.

[22].

C. J. Kim, “Adaptive acquisition of PN code in multipath fading mobile channels,” Electronics Letters, vol. 38, no. 3, pp. 135-137, Jan. 2002.

[23].

D. Borio, E. Angiuli, R. Giuliani, and G. Baldini, “Robust spectrum sensing demonstration using a low-cost front-end receiver,” International Journal of Antennas and Propagation, vol. 2015, p. 464892, Aug. 2015.

[24].

S. Rostami, K. Arshad, and K. Moessner, “Order-statistic based spectrum sensing for cognitive radio,” IEEE Communications Letters, vol. 16, no. 5, pp. 592-595, May 2012.

[25].

X. Hou, N. Morinaga, and T. Namekawa, “Direct evaluation of radar detection probabilities,” IEEE Transactions on Aerospace and Electronic Systems, vol. AES-23, no. 4, pp. 418-424, Jul. 1987.

[26].

S. Blake, “OS-CFAR theory for multiple targets and nonuniform clutter,” IEEE Transactions on Aerospace and Electronic Systems, vol. 24, no. 6, pp. 785-790, Nov. 1988.

Author Information

김 창 주 [㈜휴라/수석연구위원]

jkiees-34-7-525-i1

https://orcid.org/0000-0002-3689-8137
1980년 2월: 한국항공대학교 항공전자공학과 (공학사)
1988년 2월: 한국과학기술원 전기및전자공학과 (공학석사)
1993년 2월: 한국과학기술원 전기및전자공학과 (공학박사)
1979년 12월~1983년 3월: ADD 연구원
1983년 3월~2018년 12월: 한국전자통신연구원 (ETRI) 책임연구원
1994년 3월~1998년 12월: 한국전자통신연구원 (ETRI) 전파신호처리연구실장
1999년 1월~2001년 4월: 한국전자통신연구원 (ETRI) 이동통신모뎀연구부장
2003년 2월~2010년 12월: 한국전자통신연구원 (ETRI) 전파기술연구부장
2018년 12월~2021년 12월: 한국전자통신연구원 (ETRI) 연구전문위원
2019년 3월~2022년 2월: 한동대학교 전산전자공학부 초빙교수
2022년 3월~현재: ㈜휴라 수석연구위원
[주 관심분야] 이동통신, 무선통신, 인지 무선 등