딥러닝을 활용한 한반도 상공의 대기 굴절률 예측

전자파는 서로 다른 굴절률을 갖는 매질의 경계면에서 굴절, 반사한다. 대기권 내의 전자파의 전파 특성은 대류권, 성층권의 굴절률 변화에 의한 영향을 받으며, 굴절률은 다음과 같은 식에 의해 계산된다^[6].

식 (1)에서 N[N-units]은 굴절률, T는 기온[K], P는 기압[mbar], e[mbar]는 수증기 부분압력을 나타낸다. 그림 1은 대한민국 및 주변국의 기상관측소 위치를 나타낸다. University of Wyoming의 기상과학과 홈페이지에서는 각 지역의 기상관측소에서 측정한 고도별 기온, 기압, 상대습도에 대한 데이터를 하루 2회 제공하고 있다^[7]. 본 논문에서는 한반도 상공의 고도에 따른 2차원 굴절률을 예측하기 위해 University of Wyoming의 기상과학과 홈페이지에서 제공하는 한반도와 주변 국가의 9개 기상관측소에서 수집된 데이터를 활용된다. 표 1은 각 관측소의 관측 개시일로부터 2022년 11월 3일 00Z까지 이용 가능한 기상관측데이터의 수를 나타낸다. 본 논문에서는 총 180,000 여 개의 데이터를 학습데이터로 활용된다. 조각별 3차 에르미트 보간 다항식(piecewise cubic hermite interpolating polynomial, PCHIP)을 이용해 측정값의 고도를 1 m 간격으로 균일하게 조정함으로써 각 관측소에서 수집된 데이터들 사이에 발생하는 고도 불균일성 문제를 해결한다. 이러한 데이터 가공 과정은 각 관측소에서 수집된 모든 기상관측데이터에 적용되며 가공된 데이터는 딥러닝 모델의 학습데이터로 활용된다. 각각의 학습데이터는 특정 시점에서 각 관측소에서의 굴절률과 측정값이 존재하는 각 관측소 사이의 거리 관계에 대한 정보를 포함한다.

그림 1. | Fig. 1. 한반도를 포함한 주변국의 기상관측소 위치 | Locations of radiosonde observatories.

Download Original Figure

본 논문에서는 미관측지점의 굴절률 예측을 위해 완전 연결 신경망(fully connected neural network, FCNN) 구조를 사용하는 딥러닝 모델(DNN)을 제안한다^[8]. 제안된 모델의 입력층은 미관측지점의 위치, 관측지점의 위치, 관측지점에서의 굴절률을 입력값으로 사용하며, 은닉층을 거쳐 계산된 굴절률은 출력층에서 출력된다. 미관측지점에서의 굴절률 $\stackrel{⏜}{z}$는 식 (2)와 같이 관측지점에서의 굴절률 z의 선형조합으로 계산된다. n은 기상관측소의 수를 나타낸다. 이때 coefficient λ는 예측 모델의 등가적인 표현이며, 신경망의 학습을 통해 결정된다.

신경망의 학습은 이미 측정값을 알고 있는 지역에서의 굴절률을 모른다고 가정하고, 그 지역의 굴절률을 예측하는 방식으로 진행된다. 학습 초기에 신경망의 가중치는 무작위로 할당된 값이 사용되지만, 학습이 진행되면서 가중치는 측정값을 더 잘 예측하는 방향으로 조정되는 훈련 반복(training loop)이 진행된다. 즉, 가중치는 예측값과 측정값의 차이가 최소가 되는 방향으로 수정된다. 역전파(backpropagation) 알고리즘은 학습 과정에서 가중치와 편향을 조정하기 위한 핵심 알고리즘이며, 이러한 과정은 옵티마이저(optimizer)에 의해 수행된다.

본 논문에서 제안된 모델의 학습에 사용되는 총 180,000여 개의 학습데이터는 80 %는 훈련 세트, 15 %는 검증 세트, 5 %는 테스트 세트로 구분된다. 훈련 세트를 이용하여 학습이 진행되고, 검증 세트, 테스트 세트를 이용하여 하이퍼 파라미터 튜닝을 통해 여러 구조의 모델을 실험하고, 최적의 성능을 보이는 모델이 선정된다. 학습은 AMD Ryzen 7 5800X 8-Core Processor 3.80 GHz, 128 GB RAM, NVIDIA GeForce RTX 3070 GPU 환경에서 수행되었다. 모델의 학습에 소요된 시간은 10시간이며, 굴절률 계산에 소요된 시간은 학습이 완료된 딥러닝 모델과 크리깅에서 모두 5분 내외로, 의미있는 차이를 보이지 않는다. 학습에 사용된 하이퍼 파라미터는 batch size=32, learning rate=0.001이며, 제안된 모델은 ReLU(rectified linear unit) 함수가 은닉층의 활성화 함수로 사용된 단방향 6-layer DNN(drop out=0.2) 구조를 갖는다.

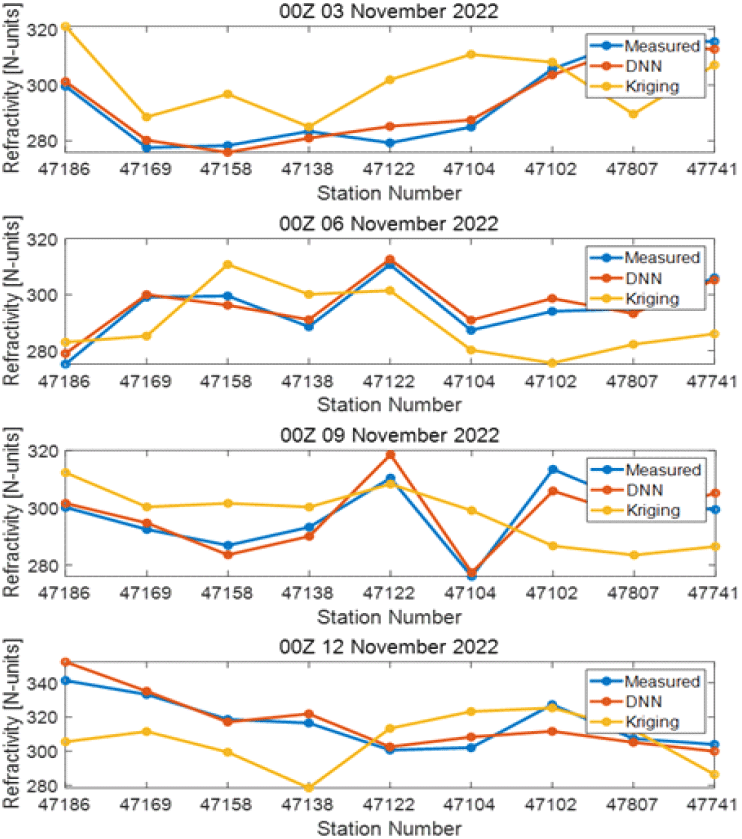
그림 2는 2022년 11월 3일 00Z부터 2022년 11월 12일 00Z까지 3일 간격으로 각 관측소에서 측정된 굴절률(measured)과 딥러닝(DNN), 크리깅(kriging)으로 예측한 굴절률을 나타낸다. 굴절률의 예측은 참값이 제공되는 관측지점에서의 굴절률을 예측하는 방식으로 진행되었다. 예를 들면 딥러닝과 크리깅을 이용한 북강릉(47102)에서의 굴절률 예측값은, 북강릉을 제외한 나머지 8개의 기상관측소의 굴절률을 이용했을 때 각각 딥러닝과 크리깅으로 예측한 값을 의미한다. 그림 2의 그래프는 모든 경우에 대해서 크리깅에 비해 딥러닝으로 예측한 값이 측정값에 더 가까움을 보여준다. 예측값이 측정값에 가까울수록 오차율이 낮으며, 이는 굴절률의 참값을 더 잘 예측할 수 있음을 의미한다. 예측값에 차이를 가져오는 요인은 학습데이터에 있다. 딥러닝 모델은 다수의 과거 데이터를 이용하여 데이터 입/출력 간의 다양한 상관관계에 대한 학습을 기반으로 미관측지점과 관측지점의 관계를 파악하기 때문에, 한 시점에 주어진 데이터들의 공간적인 상관관계를 활용하는 크리깅에 비해 더 신뢰가 높은 예측 결과를 제공할 수 있다.

그림 2. | Fig. 2. 측정값과의 차이 비교(크리깅, 딥러닝) | Refractivity by weather station (kriging, DNN).

Download Original Figure

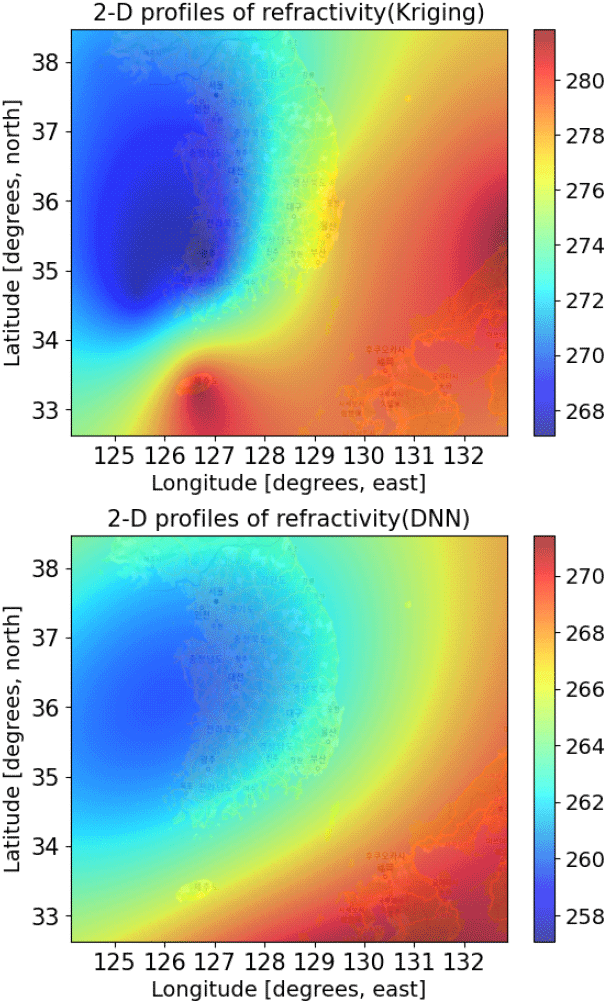
그림 3은 2022년 12월 8일 00Z의 각각 크리깅과 딥러닝을 이용하여 한반도 상공의 미관측지점에서의 굴절률을 연속적으로 나타낸 것이다. 앞선 방법론의 검증을 통해, 제안된 딥러닝 모델을 이용하면 크리깅과 비교하여 더욱 실제 대기에 가까운 굴절률 분포를 얻을 수 있다.

그림 3. | Fig. 3. 대기 굴절률 분포(크리깅, 딥러닝) | 2-D profiles of refractivity at 500 m above see level (kriging, DNN).

Download Original Figure