선박에 장착된 모노펄스 레이다의 해수면 고도 정밀 측정법 연구

I. 서 론

선박 위의 레이다는 선박 상태 등의 여건에 따라 해수면 대비 고도가 수시로 변한다. 그리고 선박 위의 레이다가 낮은 오차 수준으로 해수면 대비 고도값을 요구할 때가 있다. 예를 들면, 선박 위의 모노펄스 표적 추적 레이다는 공중의 해면밀착표적을 탐지/추적하기 위해서 해면 반사파 영향 억제 알고리즘 등을 사용하는 데, 이런 알고리즘은 대부분 레이다의 고도를 수십 센티미터 오차 수준으로 알고 있어야만 원하는 효과를 발휘한다^[1]~[3].

선박 위의 레이다의 고도를 측정하는 기존의 방법으로는 선박의 흘수선 정보 이용 및 광학 장비를 이용한 측정이 있을 수 있으나, 수시로 선박의 흘수선 정보를 수십 센티미터 오차 수준의 값으로 얻을 수가 없고, 광학 장비는 광의 해면 반사 특성 때문에 표적이 아닌 해수면에 대해 거리를 제대로 측정할 수가 없어서 미리 알려진 기준 표적이 없으면 수시로 원하는 오차 수준의 레이다 고도값을 얻을 수 없다. 레이다 장치를 이용한 기존의 방법으로는 항공기에서 사용하는 레이다 고도계라는 별도의 고도 측정 전용 레이다 장치를 이용하는 방법이 있다. 그러나 레이다 고도계는 플랫폼 하단에서 수직 방향으로 지면을 향해 빔 조사하여 고도를 직접 측정하기에 선박에는 레이다 고도계를 사용할 수 없는 환경이다. 그리고 그 측정 오차도 수 미터에서 수십 미터 수준으로 1 m 이하의 오차 수준의 플랫폼 고도값을 제공하지 못하고 있다. 또한 레이다 고도계로 고도를 측정하는 기술은 표적 탐지/추적 하는 레이다 외에 별도의 송/수신 안테나 및 레이다 장치를 필요로 한다.

전투기 레이다에서는 공대지 거리측정(AGR, air to ground ranging) 기술^[4],^[5]을 이용하여 빔 조향 위치의 거리를 측정하고, 빔 조향 위치의 고도를 추정한다. 즉, 모노펄스 레이다로 일정 고각에서 빔 조향 및 방사하여 빔 조향 위치의 거리를 측정하고 빔 조향 위치의 고도를 추정할 수 있다. 그리고 육지 지면과는 다르게 해수면의 고도는 일정하게 분포함으로 모노펄스 레이다로 빔 조향 위치의 고도뿐만 아니라, 해수면 위의 플랫폼의 고도를 추정할 수 있다. 그러나 모노펄스 레이다로 일정 고각에서 해수면에 빔 조향 및 방사하여 플랫폼의 고도를 추정할 수 있지만, 거리 측정(AGR)값 오차 및 레이다 설치 오차 등의 오차 요소 때문에 수십 센티미터 오차 수준의 고도값을 얻지 못한다. 아주 적은 레이다 설치 오차 또는 정밀한 설치 오차 보상 방법이 수반되지 않으면 기존의 단순한 공대지 거리측정값으로 고도를 추정하여 선박 위의 레이다 해수면 고도를 수십 센티미터 오차 수준으로 측정할 수 없다. 본 논문에서는 선박 위의 모노펄스 레이다가 빔을 조사하여 빔 조사 위치의 해수면에 대한 거리를 측정하고, 레이다 설치 오차를 고려하여 레이다의 해수면 대비 고도를 정밀하게 측정하는 방법을 제시한다. 제시한 방법은 레이다를 운용하는 환경에서 필요시마다 수시로 운용할 수 있으며, 적절한 파형 운영 등의 조건에서 수십 센티미터 오차 수준으로 레이다의 해수면 대비 고도값을 측정할 수 있다.

II장에서는 선박 위의 모노펄스 레이다로 AGR 기술을 이용하여 레이다의 해수면 대비 고도를 측정하는 개념을 설명하고, 거리측정 오차 및 레이다 설치 오차에 따른 레이다 고도 추정의 오차 및 한계점을 분석한다. III장은 본 논문에서 제시하는 AGR 기술과 레이다 설치 오차 추정을 통한 레이다의 해수면 대비 고도 정밀 측정법을 기술한다. Ⅳ장에서는 시뮬레이션을 통해 제안 방법의 성능 우수성을 보이며, 제안 방법이 수십 센티미터 오차 수준으로 해수면 대비 고도를 측정할 수 있는 조건을 분석한다. V장에서는 시뮬레이션을 통해 AGR 기술로 얻을 수 있는 거리측정 정확도를 분석하여 제안 방법이 모노펄스 레이다로 원하는 오차 수준으로 해수면 대비 레이다 고도를 측정할 수 있는 모노펄스 레이다 시스템의 조건을 분석하고, 제안 방법의 실용성과 효용성을 보인다.

II. 선박 위의 레이다 고도 측정과 요구 정확도

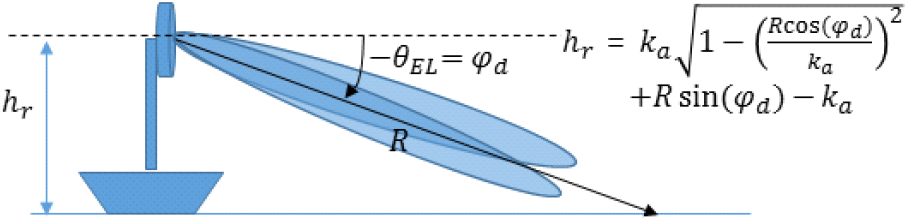
선박 위의 모노펄스 레이다가 해면밀착 공중 표적을 탐지/추적하는 경우에는 해면반사파 영향으로 표적의 고각 측정 오차가 커지게 된다. 해면반사파의 영향을 극복하고 표적 고각을 측정하는 방법들이 연구되었으며, 이런 방법들은 정확한 레이다의 고도 정보를 요구한다^[1]~[3]. 선박 위의 레이다는 여러 여건에 따라 수시로 변하며, 모노펄스 레이다로 해면밀착표적을 탐지/추적하기 위해서 필요시마다 레이다의 고도를 측정하는 것이 필요하다. 모노펄스 레이다를 이용한 AGR 기술로 레이다의 고도를 측정하면 레이다가 필요시마다 레이다의 고도를 측정할 수 있다. 그림 1은 AGR 기술 기반 레이다 고도 측정 개념을 나타낸다. 그림 1에서 −θ_EL=φ_d는 레이다의 빔조향 고각, k_a는 유효 지구반지름, R은 AGR 기술로 측정되는 레이다에서 빔조향 지면 위치까지의 거리, 그리고 h_r은 레이다의 고도를 나타낸다. 모노펄스 레이다로 일정 고각에서 빔조향 및 방사하여 빔조향 위치의 거리를 측정하고, 플랫폼의 고도를 추정하는 방법이 있다.

그림 1. | Fig. 1. AGR 기술 기반 선박 위의 레이다 고도 측정 | Measuring radar altitude on a ship based on AGR technology.

Download Original Figure

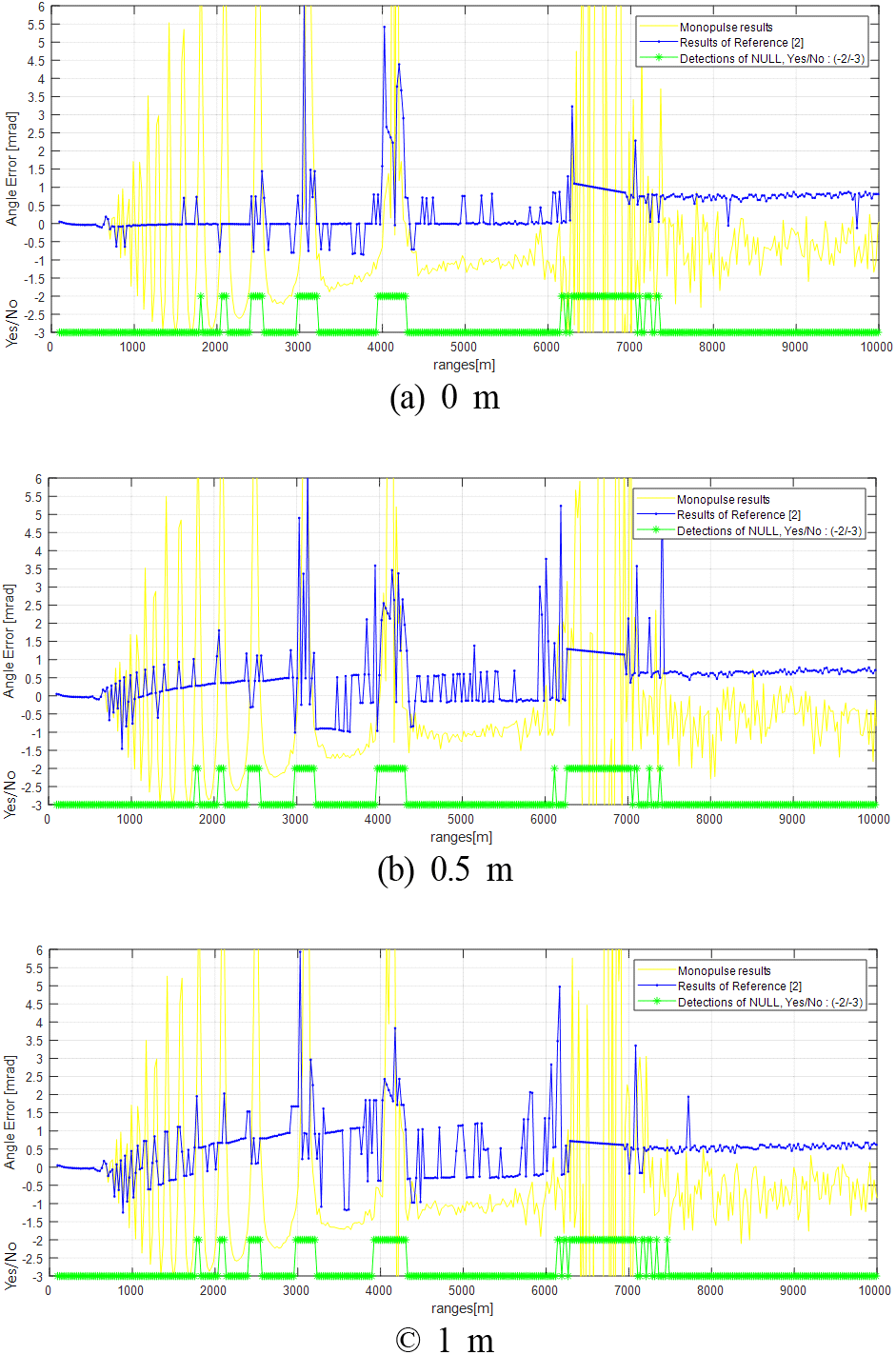
해면반사파 영향을 극복하고 표적 고각을 측정하는 방법들^[1]~[3]은 높은 정확도의 레이다의 고도 정보를 요구한다. 예를 들어, 그림 2는 선박 위의 모노펄스 레이다로 해면밀착 표적을 탐지하는 시뮬레이션을 통해 참고문헌 [2]의 방법에서 레이다 고도 정보 오차에 따른 표적 고각 측정 오차의 경향을 나타낸 것이다. 그림 2의 그래프에서 순수 모노펄스 방식으로 구한 결과(monopulse results)와 참고문헌 [2]에 의한 방식의 결과(results of reference [2])를 비교를 위해 함께 보였다. 그리고 표적의 거리 구간 중에서 해면반사파들의 상쇄 간섭 등의 요인으로 표적 반사 신호에 NULL이 발생해서 표적 고각 측정값들을 신뢰할 수 없다고 판단되는 구간(해당 구간을 그림의 그래프에서 NULL로 명칭함)을 탐지한 결과도 함께 나타내었다(“Detection of NULL, Yes/No : (−2/−3”)에서 NULL로 탐지된 구간은 −2의 값으로 NULL로 탐지되지 않은 구간은 −3으로 표기함). 그림 2에서 보듯이 참고문헌 [2]의 방법의 경우는 표적 고각을 1 mrad 이하의 오차로 측정하기를 위해서는 레이다 고도 정보를 0.5 m 이하의 오차 수준으로 요구한다(측정값들을 신뢰할 수 없는 구간의 결과들은 제외함). 본 논문에서는 논문 저술의 진행을 위해 레이다 고도 정보의 요구 정확도를 0.5 m 이내로 설정하겠다.

그림 2. | Fig. 2. 참고문헌 [2]의 방법을 이용한 표적 고각 측정에서 레이다 고도 정보 오차가 (a) 0 m, (b) 0.5 m, 및 (c) 1 m일 때의 표적 고각 측정 오차 그래프 | Graphs of target elevation measurement errors when errors of radar altitude inputs are (a) 0 m, (b) 0.5 m, and (c) 1 m in target elevation measurements using the method of reference [2].

Download Original Figure

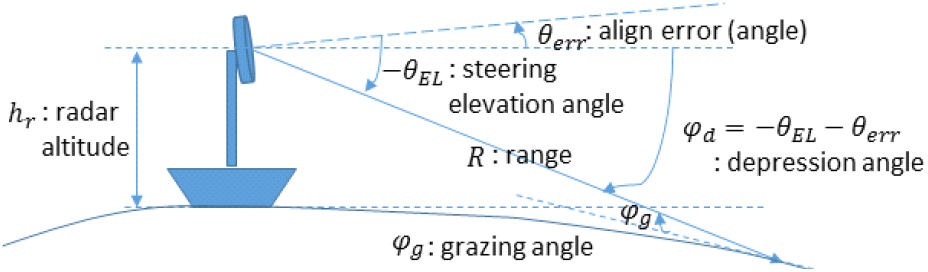
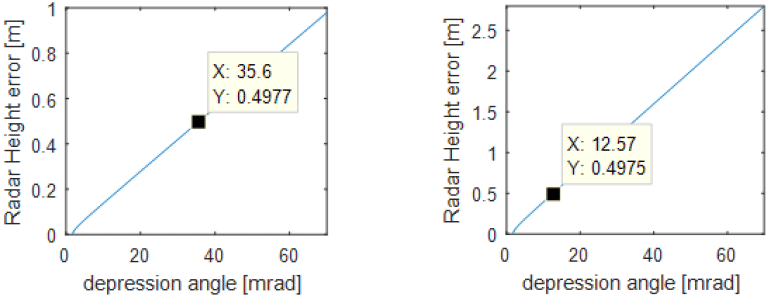
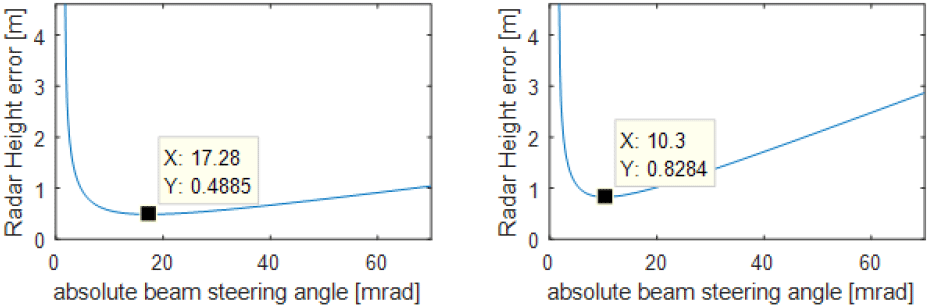
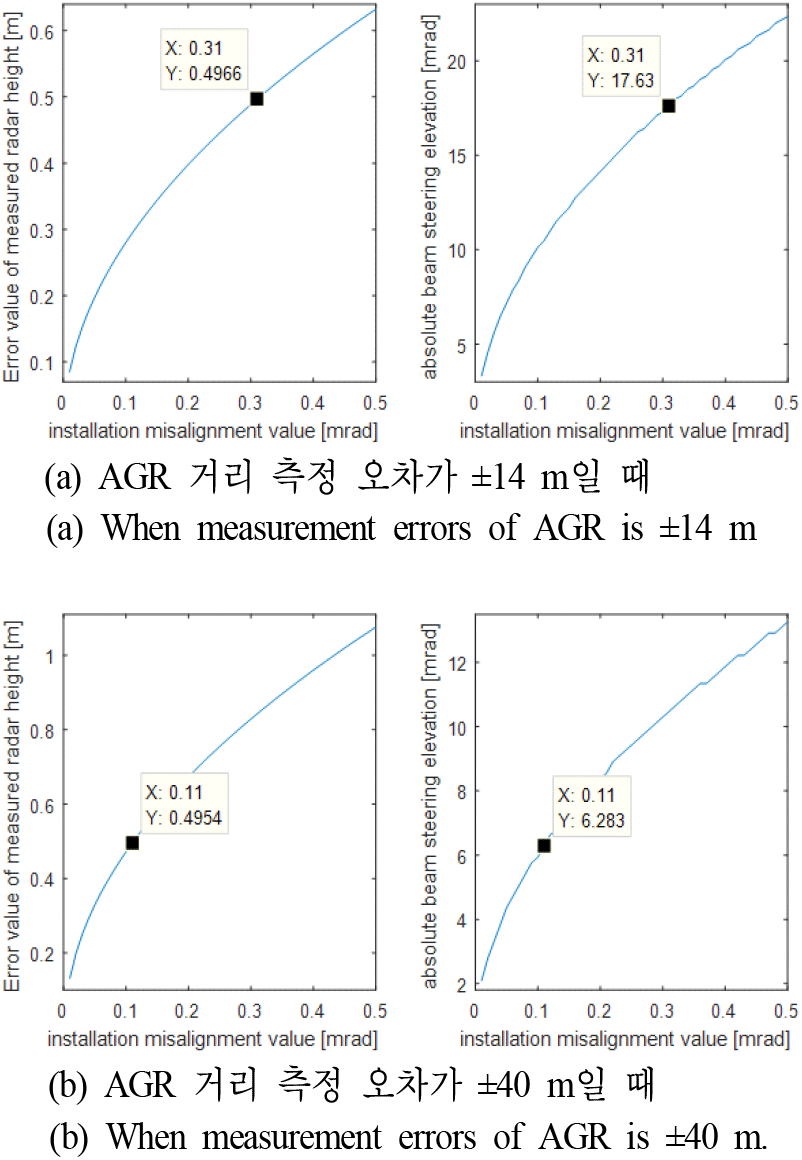
레이다 고도 정보의 요구 정확도를 0.5 m 이내로 가정하였을 때, AGR 기술을 기반한 레이다 고도 측정이 요구 정확도를 만족시킬 수 있는지 시뮬레이션을 통해 확인해 보았다. 그림 3은 관련 시뮬레이션의 기하학적 모델과 기호 정의를 나타낸다. AGR 거리 측정은 측정 오차값을 가지게 되며 이 거리 측정 오차값에 의해 레이다 고도 측정 오차가 발생한다. 또한 레이다 고각 방향 설치 오차(정렬 오차)도 레이다 고도 측정 오차를 발생시킨다. 그림 3에서 보듯이 레이다 고도 측정에 영향을 미치는 레이다의 고각 방향 설치 오차(θ_err)를 포함하고 있다. 레이다 고도 h_r=14 m로 하고(약 θ_EL=−35.6 mrad~-8.7 mrad의 빔조향 고각에서 거리 측정 가능), 먼저 θ_err=0으로 가정하여 AGR 거리 측정 오차에 따른 그림 1에 나타낸 식으로 계산한 레이다 고도 측정 오차를 그림 4에 나타내었다. 그림 4에서 좌측은 AGR 거리 측정 오차가 ±14 m일 때의 분석 결과를 그리고 우측은 ±40 m일 때의 분석 결과를 나타낸다. 그림 4의 그래프들은 내림각 φ_d(x축)에 따른 레이다 고도 계산값의 최대 오차(y축)를 보이고 있다. 그림 4에서 보듯이 레이다 설치 오차가 없다면 빔조향에 따른 내림각이 커질수록 레이다 고도 측정 오차가 커지며, 레이다 고도 측정 요구 정확도 0.5 m 이내를 만족하는 빔 조향 범위가 제한적인 것을 확인할 수 있다. 그림 4에서 보듯이 요구 정확도 0.5 m 이내를 만족하기 위해, AGR 거리 측정 오차가 ±14 m일 때는 내림각이 약 35.60 mrad이하이어야 하며 AGR 거리 측정 오차가 ±40 m일 때는 내림각이 약 12.57 mrad 이하이어야 함을 확인 할 수 있다. 참고로 AGR 거리 측정 오차는 고각 방향 조향 내림각(φ_d)이 안테나 빔 폭보다 작아지면 커지게 되므로 내림각(φ_d)을 낮추는 것이 항상 유리한 것은 아니다(이와 관련된 AGR 기술의 거리 측정 정확도에 대해서는 Ⅴ장에서 자세히 다룬다). 다시 말해서 레이다 고도가 낮은 상황(h_r=14 m)에서 조향 방향 경사 거리 측정값의 오차가 내림각(φ_d)과 상관이 없다고 가정하면 내림각(φ_d)을 작게 해야 레이다 고도값 측정 정확도에 유리하지만, AGR 기술은 안테나 빔 폭보다 내림각(φ_d)의 크기가 작으면 조향 방향 경사 거리 측정 정확도가 낮아지며 경사 거리값을 이용한 레이다 고도값 계산의 오차를 크게 할 수 있다. 그러므로 내림각을 무조건 크거나 작게 설정할 수 없고 적절하게 선택하는 것이 필요하다(Ⅳ장 및 Ⅴ장과 같은 분석 자료를 바탕으로). 실제로는 레이다 고각 방향 설치 오차가 반드시 존재하며, h_r=14 m 및 θ_err=3 mrad를 가정하여 계산한 레이다 고도 측정 오차를 그림 5에 나타내었다(그림 3의 시뮬레이션 환경에서 그림 1에 나타낸 식으로 계산). 그림 5에서 좌측은 AGR 거리 측정 오차가 ±14 m일 때의 분석 결과를 그리고 우측은 ±40 m일 때의 분석 결과이며, 레이다 설치 오차와 AGR 거리 측정 오차를 모두 고려하면 특정 조향 각도에서 레이다 고도 측정 오차가 최소가 됨을 확인할 수 있다. 그림 5에서 확인해 보면 θ_err=3 mrad, h_r=14 m일 때, AGR 거리 측정 오차가 최대 14 m이면 빔 조향 고각이 θ_EL=−17.28 mrad에서 최소의 레이다 고도 측정 오차 0.49 m를 달성하며, AGR 거리 측정 오차가 최대 40 m이면 빔 조향 고각이 θ_EL=−10.30 mrad에서 최소의 레이다 고도 측정 오차 0.83 m를 달성한다. 그림 6에서는 레이다 고각 방향 설치 오차에 따라 달성할 수 있는 레이다 고도 측정 오차의 최소값 등을 분석한 것이다(그림 3의 시뮬레이션 환경에서 그림 1에 나타낸 식으로 계산). 그림 6(a)와 그림 6(b)에서 좌측의 그래프들은 레이다의 고각 방향 설치 오차 θ_err(x축)에 따른 달성할 수 있는 레이다 고도 측정 오차의 최소값(y축)을 보이며 우측의 그래프들은 레이다의 고각 방향 설치 오차 θ_err(x축)에 따른 레이다 고도 측정 오차의 최소값을 달성하기 위해 요구되는 빔 조향 고각 θ_EL(y축)을 보인다. 그림 6(a)의 그래프에서 레이다 고도 h_r=14 m이고 AGR 거리 측정 오차가 ±14 m 및 빔 조향 고각 θ_EL=−17.63 mrad일 때 레이다의 고각 방향 설치 오차를 0.31 mrad 이하(θ_err≤0.31 mrad)로 하여야만 레이다 고도 정보의 요구 정확도(0.5 m)내에서 레이다 고도를 측정할 수 있음을 확인할 수 있다. 그리고 그림 6(b)의 그래프에서 레이다 고도 h_r=14 m이고 AGR 거리 측정 오차가 ±40 m 및 빔 조향 고각 θ_EL=−6.28 mrad일 때 레이다의 고각 방향 설치 오차를 0.11 mrad 이하(θ_err≤0.11 mrad)로 하여야만 레이다 고도 정보의 요구 정확도(0.5 m)내에서 레이다 고도를 측정할 수 있음을 확인할 수 있다. AGR 거리 측정 오차 크기 14 m 및 40 m를 고려했을 때, 그림 1에 나타낸 단순한 계산식으로 레이다 고도 정보의 요구 정확도 0.5 m 이내를 만족하기 위해서는 θ_err값의 0.31 mrad 및 0.11 mrad 이하라는 높은 정밀도의 요구 규격을 필요로 한다. 이런 높은 요구 규격의 설치 오차는 만족하기 쉽지 않다. 그러므로 레이다 고도 정보의 요구 정확도를 만족시키는 좀 더 정밀한 레이다 고도 측정법이 필요하다.

그림 3. | Fig. 3. AGR 기술 기반의 레이다 고도 측정의 기하학적 모델과 기호 정의 | Definition of geometry and notation for measuring the radar altitude based on AGR technology.

Download Original Figure

그림 4. | Fig. 4. 레이다 설치 오차 θ_err=0이고 AGR 거리 측정 오차가 ±14 m(좌) 또는 ±40 m(우)일 때, 레이다 고도 측정 최대 오차 분석 결과 | Results of max error analysis of calculating radar heights when radar elevation align error θ_err=0 and measurement errors of AGR are ±14 m (left) or ±40 m (right).

Download Original Figure

그림 5. | Fig. 5. 레이다 설치 오차 θ_err=3 mrad이고 AGR 거리 측정 오차가 ±14 m(좌) 또는 ±40 m(우)일 때, 레이다 고도 측정 최대 오차 분석 결과 | Results of max error analysis of calculating radar heights when radar elevation align error θ_err=3 mrad and measurement errors of AGR are ±14 m (left) or ±40 m (right).

Download Original Figure

그림 6. | Fig. 6. 레이다 설치 오차(θ_err)별로 달성할 수 있는 레이다 고도 측정 오차의 최소값과 요구되는 빔 조향 고각의 분석 결과 | Analysis results of the minimum achievable radar altitude measurement error and the required beam steering elevation angle for each radar elevation align error (θ_err).

Download Original Figure

Ⅲ. 레이다 설치 오차 추정을 통한 레이다 고도의 정밀 측정

이 장에서는 논문에서 제안하는 현 해수면 대비 레이다의 고도를 정밀 측정하는 방법을 설명한다. 제안한 레이다 고도 측정은 AGR 거리 측정값을 이용하여 레이다 고각 방향 설치 오차를 추정하고 설치 오차 보정 과정을 포함하는 방법이다. 레이다 고도 측정의 기하학적 모델과 기호 정의는 그림 3과 동일하다. 그림 7에 제안한 레이다 고도 측정법의 처리단계를 보였다. 단계 2)와 단계 3)은 레이다에서 지면 위에 고각 θ_EL1과 θ_EL2로 빔 조향하고 AGR 거리 측정 기술로 레이다 중심 면과 조향 지면 위치 사이의 거리 R₁과 R₂를 측정하는 단계이다. 실제로 레이다 고각 방향 설치 오차 θ_err가 존재하기 때문에 측정 거리 R₁과 R₂는 식 (1)을 따른다^[6],[7].

그림 7. | Fig. 7. 제안한 레이다 고도 측정법의 처리단계 | The proposed procedure of measuring radar altitude.

Download Original Figure

기서 φ_d=−θ_EL-θ_err이다. 단계 4)에서는 R₁과 R₂의 거리 측정에서 레이다 고도는 변화하지 않는다는 사실에 근거하여 레이다 고각 방향 설치 오차 θ_err를 추정하며, 식 (1)을 이용하여 E를 정의하고 E²이 최소가 되는 θ_err값을 경사하강법(gradient-descent method)^[8]으로 구한다.

경사하강법을 위해 기술하면 dE²/dθ_err=2E(dE/dθ_err)이며 dE/dθ_err는 다음과 같다.

경사하강법으로 초기치 θ_err=0으로 시작하고 다음의 조건에 수렴할 때 까지 ${\theta }_{err}^i$ 를 갱신하여 최종 θ_err을 구한다.

본 논문에서는 η=10⁻⁹, th_converge=10⁻¹²로 설정한다. 그림 8은 그림 7의 단계 4)에서 경사하강법으로 레이다 설치 오차 θ_err를 추정하는 순서도를 나타낸다.

그림 8. | Fig. 8. θ_err을 추정하는 순서도 | Flowchart for estimating θ_err.

Download Original Figure

그림 7의 단계 5)에서는 추정한 최종 θ_err와 측정한 R₁과 R₂ 및 식 (1)을 사용하여 식 (5)와 같이 레이다 고도를 계산한다. 제안한 방법은 그림 7의 단계 6)에서 식 (5)로 계산한 $h_r{}_{{}_{measure}}$ 를 레이다 고도 측정치로 출력한다.

제안한 방법에서 거리 측정 오차가 존재하면 레이다 설치 오차 추정치에 오차가 존재하고 레이다 고도 측정치에도 오차가 존재하게 된다. 그래서 거리 측정 오차가 존재할 때 제안한 방법의 레이다 고도 측정 성능을 확인할 필요가 있다. Ⅳ장에서는 거리 측정 오차 및 레이다 설치 오차가 존재하는 상황에서 제안한 방법의 성능을 분석한다. 참고로 대부분 레이다 설치 오차는 처음 레이다를 설치할 때 고정된 값으로 정해질 것이며, 시간이 지나 레이다 설치 오차가 거의 같은 값을 유지하거나 아주 조금씩 달라질 가능성도 있을 것이다. 제안한 방법은 레이다 설치 오차가 시간이 지나서 달라지더라도 상관없이 필요시마다 레이다 운용 중에 사용할 수 있으며, 원하는 측정 성능을 유지하도록 설계할 수 있다(Ⅳ장의 거리 측정 오차 및 레이다 설치 오차에 따른 제안한 방법의 성능 분석을 통해 허용 가능한 레이다 설치 오차 및 거리 측정 오차를 확인하여 설계에 반영할 수 있다).

IV. 레이다 고도 측정법의 성능 분석

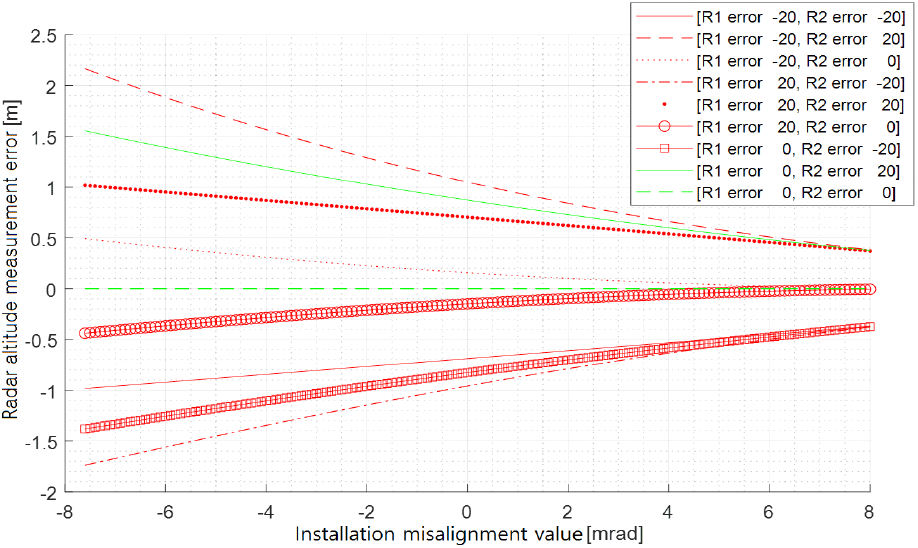
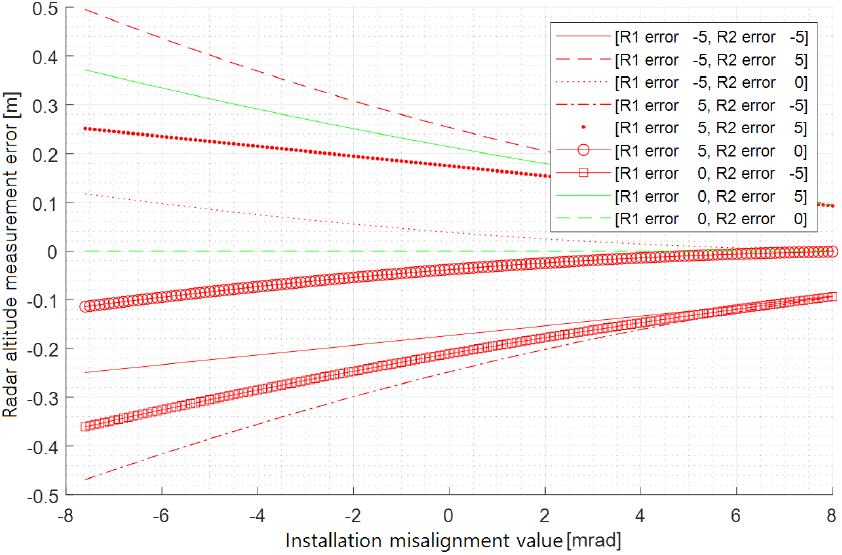
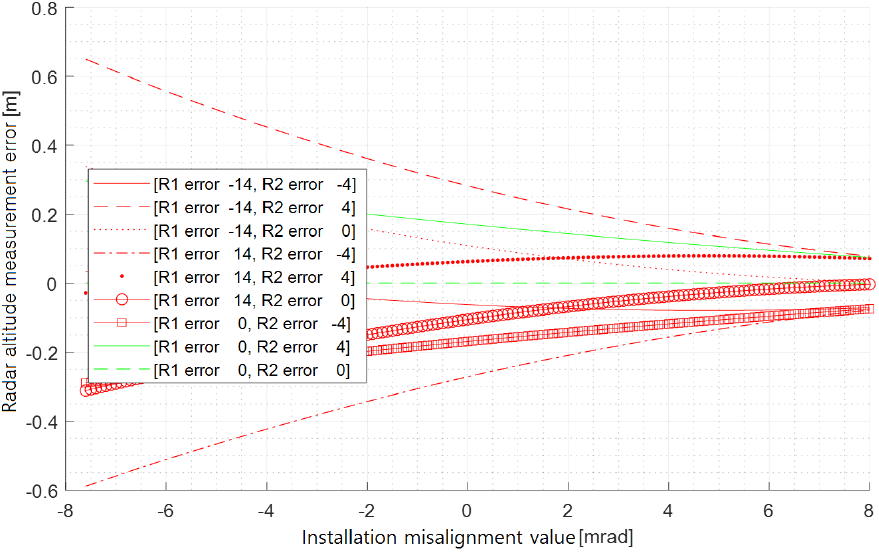
이 장에서는 레이다 설치 오차와 AGR 거리 측정 오차에 따른 제안한 방법의 레이다 고도 측정 성능을 확인해 본다. 레이다 고도 측정 요구 정확도 규격을 0.5 m 이내로 가정하고 h_r=14 m일 때 시뮬레이션을 통해 제안한 방법의 성능을 분석해 봤다. 먼저 θ_EL1=−10.47 mrad, θ_EL2=−24.43 mrad, AGR 거리 측정에 의한 거리 R₁과 R₂의 측정 오차가 최대 ±20 m까지 날 때, 시뮬레이션을 통해 레이다 설치 오차(정렬 오차)에 따른 레이다 고도 측정 오차를 그림 9에 나타내었다. 그림 9에서 레이다 설치 오차에 따른 레이다 고도 측정 오차들은 AGR 거리 측정 오차 R₁이 −20 m와 R₂가 +20 m 오차인 그래프와 R₁이 +20 m와 R₂가 −20 m 오차인 그래프 사이의 영역 내에 존재한다. 시뮬레이션 결과로 보면 레이다 설치 오차가 +값을 가질 때 제안 방법의 레이다 고도 측정 오차가 적다. AGR 거리 측정 오차의 최대가 ±20 m 이내이고 설치 오차가 +6.2 mrad 이상이면 가정한 요구 정확도 규격(0.5 m) 내에서 레이다 고도를 측정할 수 있다. 상대적으로 높은 설치 오차에도 원하는 레이다 고도 측정 정밀도를 얻을 수 있다. 본 제안 방법으로 레이다 고도값을 측정할 때에 되도록 설치 오차가 +값을 가지도록 하는 것이 유리하다. 또한 θ_EL1=−10.47 mrad, θ_EL2=−24.43 mrad, AGR 거리 측정에 의한 거리 R₁과 R₂의 측정 오차가 최대 ±5 m까지 날 때, 시뮬레이션을 통해 레이다 설치 오차에 따른 레이다 고도 측정 오차를 그림 10에 나타내었다. 그림 10에서 AGR 거리 측정 오차의 최대가 ±5 m 이내이고 설치 오차가 −7.6 mrad 이상이면 요구 정확도 0.5 m 내에서 레이다 고도를 측정할 수 있음을 확인할 수 있다. 참고로 AGR 거리 측정 기술을 이용한 거리 측정은 빔 조향 고각의 크기가 레이다의 고각 빔 폭보다 커야 최적 성능을 보인다. 그리고 파형의 거리 해상도가 좋아야 유리하다. 그래서 빔조향 고각 θ_EL1=−10.47 mrad 및 θ_EL2=−24.43 mrad에서 AGR 거리 측정 기술로 거리 측정 오차가 ±5 m 이내를 얻기 위해서는 고각 빔 폭은 10.47 mrad 이하, 파형의 거리 해상도는 10 m 이하가 되도록 해야 할 것이다. 마지막으로 θ_EL1=−10.47 mrad, θ_EL2=−24.43 mrad, AGR 거리 측정에 의한 거리 R₁과 R₂의 측정 오차가 R₁에서 최대 ±14 m, R₂에서 최대 ±4 m까지 날 때, 시뮬레이션을 통해 레이다 설치 오차에 따른 레이다 고도 측정 오차를 그림 11에 나타내었다. 본 제안 방법은 두 번의 고각 조향에 의한 거리 측정에서 한 번의 고각 조향각은 작을수록 그리고 다른 한 번의 고각 조향각은 처음 고각 조향각과 차이가 어느 정도 크게 날수록 레이다 고도 측정 성능이 좋아진다. 이런 특징을 반영하여 그림 11에서 고각 빔 폭을 20.94 mrad, 레이다 파형의 거리해상도를 10 m로 가정하고 R₁과 R₂의 측정 오차를 R₁에서 최대 ±14 m, R₂에서 최대 ±4 m까지로 하여 시뮬레이션을 행한 것이다(첫 번째 고각 조향 θ_EL1은 고각 빔 폭보다 크기가 작아서 R₁의 측정 오차를 최대 ±14 m로 함). 그림 11에서 레이다 설치 오차가 −5 mrad 이상이면 요구 정확도 0.5 m 내에서 레이다 고도를 측정할 수 있음을 확인할 수 있다. 즉 레이다 설치 오차의 절대 크기가 5 mrad보다 작으면 레이다 고도를 ±0.5 m 오차 이내에서 측정할 수 있다.

그림 9. | Fig. 9. 레이다 고도 측정 성능 분석 그래프 1 | Analysis graph 1 for radar altitude measurement performance.

Download Original Figure

그림 10. | Fig. 10. 레이다 고도 측정 성능 분석 그래프 2 | Analysis graph 2 for radar altitude measurement performance.

Download Original Figure

그림 11. | Fig. 11. 레이다 고도 측정 성능 분석 그래프 3 | Analysis graph 3 for radar altitude measurement performance.

Download Original Figure

제안한 방법은 별도의 플랫폼 고도 측정 장비 없이 표적을 탐지/추적하는 모노펄스 레이다 운용 상황에서 필요시 수시로 운용하여 상대적으로 낮은 오차 수준으로(±0.5 m 이내) 지면(해수면) 대비 플랫폼 고도를 측정할 수 있다. 또한 비교적 낮은 플랫폼 고도(20 m 이하)에서 빔조향 고각의 크기를 크게 하지 못하는 상황에서(빔조향 고각의 크기가 35.6 mrad 이하)도 플랫폼 고도를 낮은 오차 수준으로 측정할 수 있다. 그리고 낮은 플랫폼 고도에서도 AGR 거리 측정 기술 외에 조향 방향의 지면 거리를 최대 ±5 m 오차로 측정할 수 있다면 본 제안 방법에 제시한 고각 방향 설치 오차 추정 및 플랫폼 고도 측정 방법을 이용하여 플랫폼 고도를 측정하면 고각 방향 설치 오차의 크기가 7.6 mrad까지 생기더라도 플랫폼 고도를 ±0.5 m 오차 이내에서 측정할 수 있다. 추가로 그림 9에서 그림 10까지의 시뮬레이션 결과가 유용한가를 확인하기 위해서는 AGR 거리 측정 기술로 θ_EL1=−10.47 mrad, θ_EL2=−24.43 mrad, h_r=14 m 등의 조건에서 AGR 거리 측정 오차가 얼마나 발생하는지 실제 실험 및 시뮬레이션을 통해 확인해 볼 필요가 있다. 다음 장에서는 시뮬레이션을 통해 AGR 기술의 거리 측정 정확도를 분석한다.

V. 시뮬레이션을 통한 AGR 거리 측정 정확도 분석

그림 3의 기하학적 정의에서 θ_err=0 및 h_r=14 m를 가정하고, 분석을 위한 시뮬레이션을 행하였다. AGR을 위한 레이다 파형은 2가지를 사용하여 비교 분석하였다. 표 1은 AGR 거리 측정 시뮬레이션에 사용한 레이다 관련 파라메타와 운용 파형을 나타낸다. 표 1의 경우 1(Case 1)은 안테나 고각 빔 폭이 20.94 mrad로 좁고, 펄스 압축 후에 거리 해상도가 10 m 미만이 되어(chirp 신호의 대역폭이 15 MHz) 비교적 작은 크기의 고각 방향 조향각에서 AGR 거리 측정 오차가 적은 레이다인 경우이다. 표 1의 경우 2는 안테나 고각 빔 폭이 100.7 mrad로 상대적으로 넓고 펄스 압축 후에 거리 해상도가 30 m 미만이 되어(chirp 신호의 대역폭이 5 MHz) 상대적으로 큰 크기의 고각 방향 조향각에서 AGR 거리 측정의 성능이 보장되는 레이다인 경우이다. 본 논문의 AGR 거리 측정을 위한 신호처리에서는 레이다 신호 전력의 축적(integration)을 위해 64개의 버스트(burst) 펄스들을 축적하여 처리했다. AGR 거리 측정의 시뮬레이션을 위해서는 지면 클러터 모의가 필요하다. 클러터는 점 클러터들을 레이다 바로 아래에서부터 레이다 지평선까지 2 m 간격으로 배치하여 모사했다. 그리고 배치된 점 클러터들의 RCS(radar cross section)은식 (6)과 같이 크기와 위상에 난수를 첨가했다.

여기서 (RCS)_i는 i번째 점표적의 RCS, σ_c는 점표적들의 평균 RCS, R_(lognormal)(i)은 로그노말(lognormal) 분포^[9]의 i번째 난수, 그리고 R_normal (i)은 정규분포의 i번째 난수를 나타낸다. 식 (6)의 σ_c의 값은 레이다의 운용 주파수와 지면 환경, 레이다 빔 폭 등을 고려하여 결정할 수 있다. 그림 12는 식 (6)의 σ_c값을 결정하기 위한 기하학적 모델 및 기호정의를 보인다. 레이다는 해수면 위의 h_r 고도에서 움직이지 않으며, 레이다 점 클러터 반사파 신호의 에너지는 안테나 방위 방향 빔 폭(ψ)과 점 클러터들의 위치 간격(시뮬레이션 모델에서는 rΔ=2 m)에 의해 결정되는 클러터 패치(patch)의 면적(S)에서 반사되어 오는 반사파 에너지로 생각한다. 그림 12의 시뮬레이션 모델에서 나타낸 안테나 주엽 빔 내에 점 클러터들의 RCS 계산을 위한 σ_c값은 식 (7)로 계산한다.

그림 12. | Fig. 12. 점 클러터 모의를 위한 기하학과 기호정의 | Definition of geometry and notation for simulating point clutters.

Download Original Figure

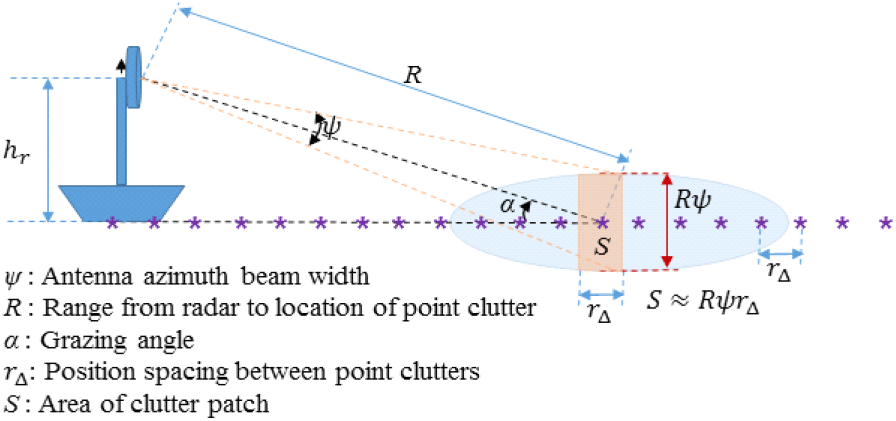
여기서 ρ는 클러터 반사계수(reflectivity)이며 시뮬레이션에서는 NRL(naval research lab.) 해상클러터 반사계수 모델^[10]을 이용하여 ρ의 값을 선정하였다. 그림 13은 NRL 모델에 기반한 지표각(grazing angle, α)별 반사계수 그래프를 나타낸다. 그림 13의 좌측 그래프는 레이다 전송주파수가 12.5 GHz일 때의 반사계수이며 우측 그래프는 9.5 GHz일 때의 반사계수이다. 그림 13의 그래프에서 NRL SS0 및 NRL SS1 등은 NRL의 해상상태 0 모델 및 해상상태 1 모델 등의 반사계수 그래프를 표현한 것이다. 그림 13의 반사계수 그래프를 이용하여 ρ의 값을 선정하고, 주엽 빔 내에 점 클러터들의 σ_c을 계산해 본다. 그림 12에서 h_r=14 m, Ψ=20.94 mrad, α=6.98 mrad(반사 계수값이 작은 안 좋은 상황 고려), r_Δ=2 m, 해상 상태는 NRL SS3(보통의 해상 상태), 운용주파수는 12.5 GHz 등을 가정하면 R=1,939 m, ρ=10^(-43.2/10)(그림 13의 좌측의 NRL SS3 그래프에서 α=6.98 mrad일 때의 반사계수 −43.8 dB 이용)이며, 식 (7)로부터 σ_c=0.0039를 얻을 수 있다. 그리고 h_r=14 m, Ψ=100.7 mrad, α=6.98 mrad, r_Δ=2 m, 해상 상태는 NRL SS3, 운용주파수는 9.5 GHz 등을 가정하면 R=1,939 m, ρ=10^(−45.6/10)(그림 13의 우측의 NRL SS3 그래프에서 α=6.98 mrad일 때의 반사계수 −45.6 dB 이용)이며, 식 (7)로부터 σ_c=0.0108을 얻을 수 있다. 표 1의 경우 1의 시뮬레이션 파라미터와 σ_c=0.0039 및 h_r=14 m, Ψ=20.94 mrad, r_Δ=2 m, 운용주파수 12.5 GHz 등을 가정하여 AGR 거리 측정 시뮬레이션을 100번 수행한 결과의 거리 측정 오차를 그림 14에 나타내었다. 그림 14(a) 및 그림 14(b), 그림 14(c)는 각각 고각 빔 조향 θ_EL을 −10.47 mrad 및 −20.94 mrad, −24.43 mrad로 한 경우의 결과이다. 그리고 표 1의 경우 2의 시뮬레이션 파라미터와 σ_c=0.0108 및 h_r=14 m, Ψ=100.7 mrad, r_Δ=2 m, 운용주파수 9.5 GHz 등을 가정하여 AGR 거리 측정 시뮬레이션을 100번 수행한 결과의 거리 측정 오차를 그림 15에 나타내었다. 그림 15(a) 및 그림 15(b), 그림 15(c)는 각각 고각 빔 조향 θ_EL을 −13.96 mrad 및 −24.43 mrad, −31.42 mrad로 한 경우의 결과이다. 그림 14 및 그림 15의 전체적인 결과를 볼 때 AGR 기술로 거리 측정하면 빔 조향 고각의 절대값이 안테나 고각 빔 폭 이상은 되어야만 AGR 거리 측정 정확도가 보장되며 높아지는 것을 확인할 수 있다. 그리고 안테나의 빔 폭이 좁고, 파형의 거리해상도가 좋을수록 AGR 거리 측정 정확도가 높아지는 것을 확인할 수 있다. 그림 14(a)에서 측정 오차의 평균이 −0.32 m이고 표준편차가 13.76 m인 것을 보면 AGR 거리 측정 오차가 ±14 m이내를 만족할 수 있을 것이다(여러 번의 AGR 거리 측정값을 평활화해서 사용한다면). 그리고 그림 14(b)에서 측정 오차의 평균이 0.03 m이고 표준편차가 2.95 m인 것을 보면 AGR 거리 측정 오차가 ±3 m 이내를 만족할 수 있을 것이다. 또한 그림 14(c)에서 측정 오차의 평균이 0.22 m이고 표준편차가 3.57 m인 것을 보면 AGR 거리 측정 오차가 ±4 m 이내를 만족할 수 있을 것이다. 그림 15(a)에서 측정 오차의 평균이 1.26 m이고 표준편차가 15.57 m인 것을 보면 AGR 거리 측정 오차가 ±17 m 이내를 만족할 수 있을 것이다. 그리고 그림 15(b)에서 측정 오차의 평균이 15.45 m 및 표준편차가 26.20 m인 것을 보면 AGR 거리 측정 오차가 ±42 m 이내를 만족할 수 있을 것이다. 또한 그림 15(c)에서 측정 오차의 평균이 18.16 m이고 표준편차가 25.14 m인 것을 보면 AGR 거리 측정 오차가 ±43 m이내를 만족할 수 있을 것이다.

그림 13. | Fig. 13. 레이다 전송주파수가 12.5 GHz(좌)와 9.5 GHz(우)일 때의 NRL 모델의 반사계수 | Reflectivity of NRL model when radar transmission frequency is 12.5 GHz (left) and 9.5 GHz (right).

Download Original Figure

그림 14. | Fig. 14. AGR 거리 측정 시뮬레이션 결과 1 | Result 1 of AGR range measurement simulation.

Download Original Figure

그림 15. | Fig. 15. AGR 거리 측정 시뮬레이션 결과 2 | Result 2 of AGR range measurement simulation.

Download Original Figure

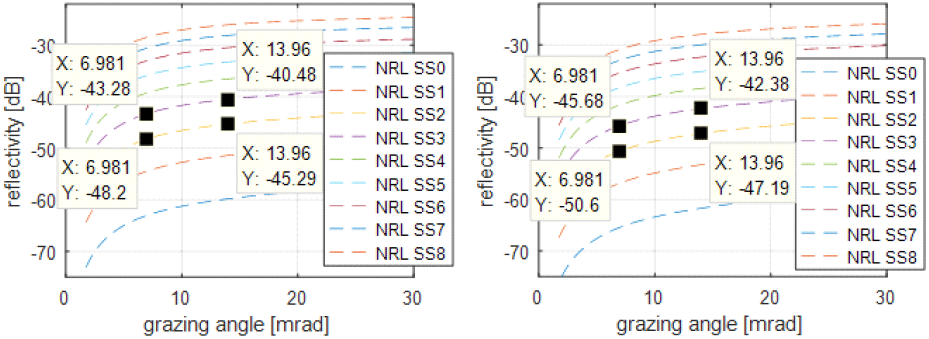
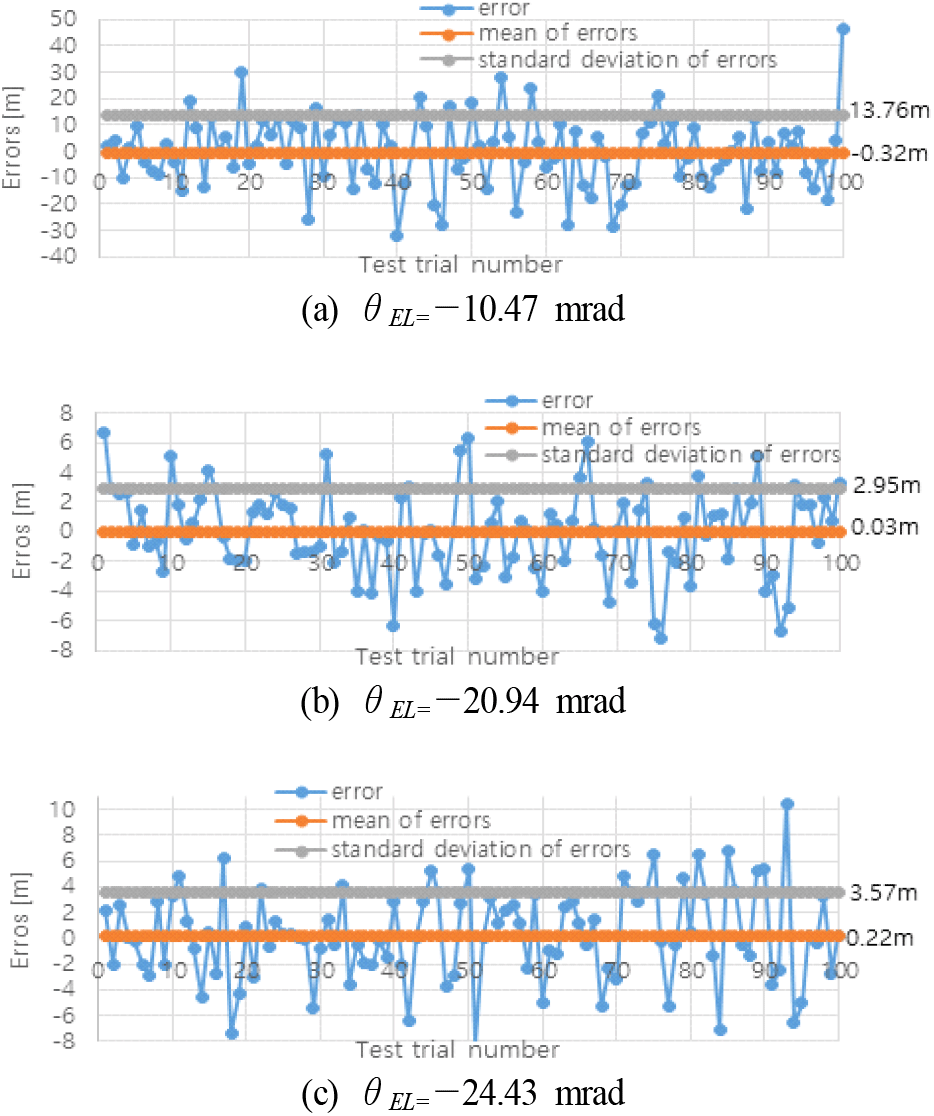
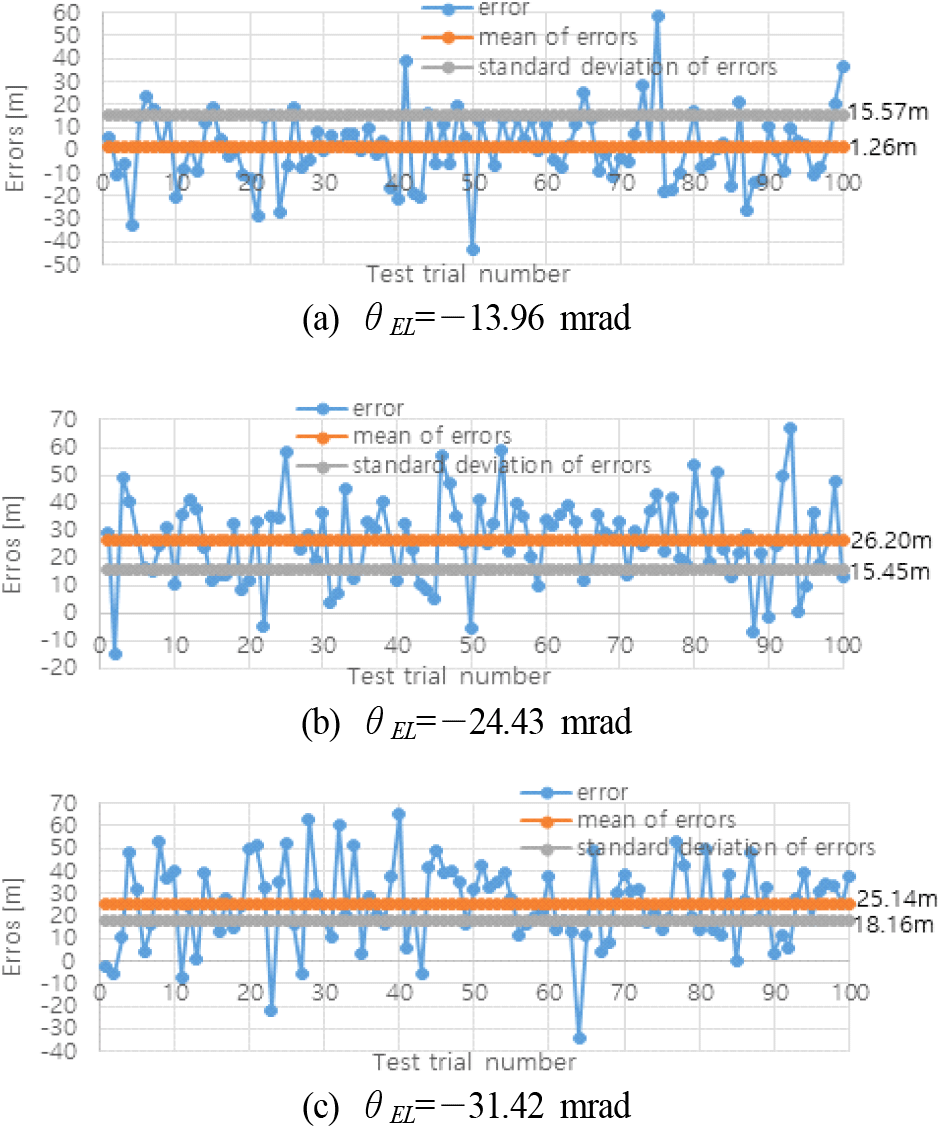
그림 14와 그림 11의 시뮬레이션 결과를 통해서, 거리 해상도 10 m 파형과 Ψ=20.94 mrad을 사용하고 빔 조향 고각 θ_EL=−24.43 mrad~−10.47 mrad 사이의 2가지 조향각에서 AGR 거리를 측정하면 거리 측정 오차는 ±14 m이내를 유지할 수 있으며 θ_EL1=−10.47 mrad, θ_EL2=−24.43 mrad로 하여(거리측정 오차에서 R₁은 ±14 m, 그리고 R₂는 ±4 m 정도) 제안한 알고리즘을 사용하면 레이다 안테나 고각 방향 설치 오차의 크기가 5 mrad 이내일 때 레이다 고도값 측정 오차는 ±0.5 m 이내를 유지할 수 있음을 확인할 수 있다. 즉 제안한 알고리즘의 유효성을 확인할 수 있다. 참고로 거리 해상도 30 m 파형과 Ψ=100.7 mrad을 사용하고 빔 조향 고각 θ_EL=−31.42 mrad~−13.96 mrad 사이의 2가지 조향각에서 AGR 거리를 측정하면 거리 측정 오차는 ±43 m 이내를 유지할 수 있으며 θ_EL1=−13.96 mrad, θ_EL2=−31.42 mrad로 하여(거리측정 오차에서 R₁은 ±17 m, 그리고 R₂는 ±43 m 정도) 제안한 알고리즘을 사용하더라도 원하는 레이다 고도값 측정 오차 규격(±0.5 m 이내)을 만족 못할 수도 있다.

VI. 결 론

선박 위의 레이다에서 해면밀착표적의 탐지/추적하기 위한 상황 등에서 낮은 오차 규격(±0.5 m 이내)으로 레이다 고도값을 요구하는 경우가 있다. 선박 위에서 표적을 탐지/추적하는 모노펄스 레이다가 별도의 다른 장비 없이 모노펄스 레이다 자체만으로 상대적으로 낮은 오차 수준으로(±0.5 m 이내) 지면 대비 고도값을 필요시 수시로 측정할 수 있는 방법을 제안하였다. 제안한 방법은 레이다 고각 방향 설치 오차가 다소 존재하는 상황에서도 성능을 유지하도록 설계하였으며 레이다의 고각 방향 설치 오차가 +값을 가질수록 더 좋은 레이다 고도 측정 정확도 성능을 보이는 특징이 있다. 또한 비교적 낮은 레이다 고도(20 m 이하)에서 안테나 빔 조향 고각의 크기를 크게 하지 못하는 상황에서(빔 조향 고각의 크기가 35.6 mrad이하)도 레이다 고도를 낮은 오차 수준으로 측정할 수 있다. 시뮬레이션을 통해 제안한 방법의 효용성 및 다음의 사항들을 확인하였다. 먼저 레이다 고도 14 m, 안테나 고각 빔 폭 20.94 mrad 이내 및 파형의 거리 해상도 10 m 이내인 레이다가 두 번의 고각 방향 빔 조향에서 첫 번째 θ_EL1=−10.47 mrad 및 두 번째 θ_EL2=−24.43 mrad로 조향하여, AGR 거리측정 기술로 측정한 거리의 측정 오차가 첫 번째는 측정 거리 R₁에서 ±14 m 이내 및 두 번째는 측정 거리 R₂에서 ±4 m 이내를 만족하고 레이다 고각 방향 설치 오차의 크기가 5 mrad 이내를 만족하면 제안한 방법으로 레이다 고도를 ±0.5 m 오차 이내에서 측정할 수 있다. 고각 방향 빔 조향값 θ_EL1 및 θ_EL2의 선택은 Ⅱ장과 Ⅳ장에서 기술했듯이 레이다의 고도에 따라 달라지며 절대값이 작을수록 그리고 두 값의 차이가 클수록 좋다. 그리고 AGR 거리 측정 기술이 안테나 고각 방향 빔 폭보다 고각 방향 조향각을 크게 해야 거리 측정 성능이 좋아진다는 것도 같이 고려해야 한다. 즉 무조건 θ_EL1 및 θ_EL2의 값을 크게 하거나 작게 할 수 없고 최적의 성능을 발휘하도록 적절해야 한다. 예를 들어 Ⅱ장에서 기술하였듯이 레이다 고도 h_r=14 m일 때는 빔 조향 고각의 절대값은 35.6 mrad 이내로 하여야 할 것이며, 사용하는 레이다의 고각 방향 빔 조향각에 따른 AGR 거리 측정 성능 자료를 바탕으로 Ⅳ장과 같은 분석 과정을 통해 θ_EL1 및 θ_EL2의 값을 설정해야 할 것이다. 그리고 낮은 플랫폼 고도에서도 AGR 거리 측정 기술 외에 조향 방향의 지면 거리를 최대 ±0.5 m 오차로 측정할 수 있다면 본 발명에 제시한 고각 방향 설치 오차 추정 및 고도 측정 방법을 이용하여 플랫폼 고도를 측정하면 고각 방향 장착 오차의 크기가 7.6 mrad까지 생기더라도 플랫폼 고도를 ±0.5 m 오차 이내에서 측정할 수 있다.