Ⅰ. 서 론
일반적으로 재머는 고출력의 전력을 방사하거나 레이다 신호를 모방한 신호를 방사함으로써 레이다를 기만하거나 레이다의 표적 탐지/추적을 방해한다. 고출력의 잡음 재밍 신호는 레이다의 수신 포화를 유발하거나, 표적 신호를 잡음 신호 속에 잠식시켜 레이다의 표적 탐지/추적 성능을 저하시키는 등 정상적 운용을 방해한다.
최신 레이다들은 이러한 고출력 재밍에 의한 레이다 열화 방지를 위해 다양한 항재밍 기능들을 탑재하고 있으며, 신호 공간 정보를 활용하여 재밍 신호를 억제하는 적응 빔형성이 있다. 적응 빔형성 기술은 안테나 소자의 가중치(weight)를 조절하여 원하는 신호 방향으로는 빔을 형성하고 재밍 신호 방향으로는 널링(nulling)을 형성한다. 이를 통해, 신호대 간섭 및 잡음 비율(signal to interference plus noise ratio, SINR)를 향상시킴으로써 재밍을 효과적으로 대응할 수 있다. 레이다가 적응형 빔을 형성하기 위해서는 노이즈 및 재밍 신호 등 레이다 주변 신호 공간에 대한 정보 수집이 필요하다. 이에, 레이다는 listening period 동안 수신 신호(received signal) N개(snapshot)를 수집하고, 수집된 신호를 바탕으로 빔형성 가중치를 도출함으로써 표적 식별에 불필요한 신호들을 억제할 수 있다.
본 논문에서는 재밍 억제를 위한 비지도 학습 기반의 컨볼루션 신경망(convolutional neural networks, CNN)을 활용한 적응형 빔형성 네트워크를 제안한다. 제안된 네트워크는 레이다가 수신한 신호를 기반으로 부배열 안테나 단위의 공분산 행렬(covariance matrix)을 입력받으면 공분산 행렬에서의 가중치 추정을 위한 피처 맵(feature map)을 추출하고 원하는 신호 방향으로는 최대로 수신하면서 재밍 신호 방향으로는 널링을 형성하는 적응형 빔형성 가중치를 추정한다. 제안된 네트워크의 성능을 확인하기 위해 대표적인 재밍 억제 목적의 적응형 빔형성 기술인 LCMV(linearly constrained minimum variance)[1] 및 CSC (conventional sidelobe canceller)[2]와 성능 비교를 수행하였다.
본 논문의 구성은 다음과 같다. Ⅱ장에서는 제안하는 적응 빔형성 가중치 추정 네트워크 구조에 대해 설명하고, Ⅲ장에서는 네트워크를 학습하기 위한 데이터셋 구성에 대해 설명한다. Ⅳ장에서는 비지도 학습 기반의 네트워크 학습 방법에 대해 설명하고, Ⅴ장에서는 LCMV 및 CSC와 성능을 비교/분석하며, Ⅵ장에서 결론을 맺는다.
Ⅱ. 적응형 빔형성 가중치 추정 네트워크 구조
제안된 네트워크의 구조는 그림 1과 같이 부배열 안테나 단위의 수신 신호 공분산 행렬에서의 피처 맵을 추출하기 위한 CNN 기반의 특징 추출기(feature extrator)와 추출된 특징을 바탕으로 적응형 빔형성 가중치를 추정하기 위한 가중치 추정기(weight estimator)로 구성되어 있다. 네트워크의 학습은 특징 추출기와 가중치 추정기가 독립적으로 이루어지는 것이 아닌 상호 동시에 재밍 억제에 수렴하는 방향으로 학습이 진행된다. 학습 초기에 특징 추출기는 네트워크에 입력된 공분산 행렬로부터 가중치 추정과 상관성이 낮은 피처 맵을 추출하게 되나, 학습이 진행됨에 따라 가중치 추정기가 적응형 빔형성 가중치를 추정하기 위한 의미있는 피처 맵을 추출하도록 특징 추출기 내부 계층의 커널 가중치들이 수렴하게 된다. 특징 추출기와 마찬가지로 가중치 추정기 역시 학습 초기에는 낮은 성능을 갖는 빔형성 가중치를 추정하게 되나, 학습이 진행됨에 따라 특징 추출기가 의미있는 특징을 추출하게 되면서 가중치 추정기 내부 계층의 노드 가중치들도 재밍 억제에 효과있는 빔형성 가중치를 추정하게 된다.
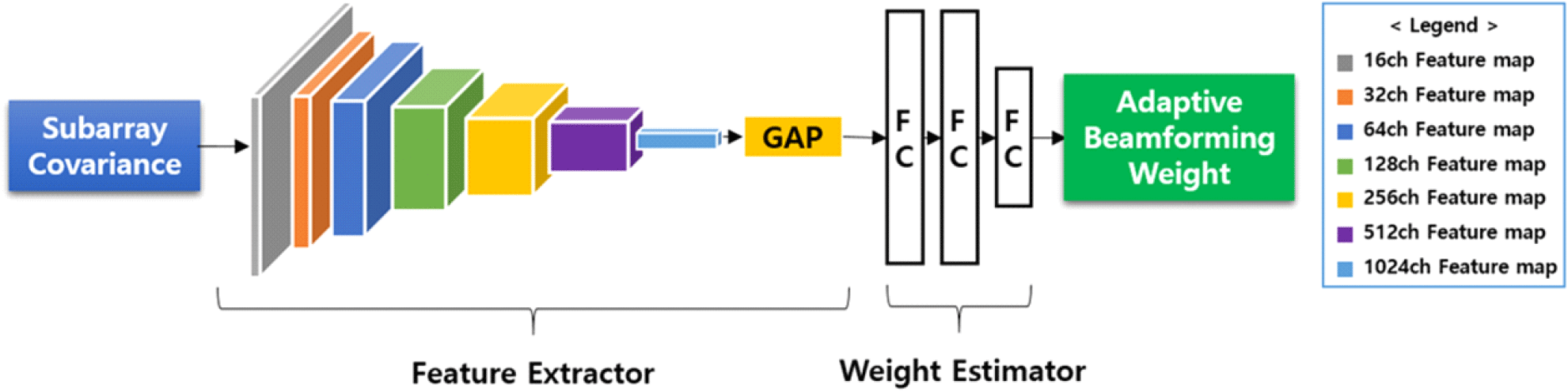
특징 추출기는 부배열 안테나 단위의 수신 신호를 기반으로 공분산 행렬로부터 적응형 빔형성 가중치를 추정하기 위한 CNN으로 구성되어 있다. 공분산 행렬은 복소수로 구성된 행렬로, CNN에서 컨볼루션 연산을 수행하기 위해서는 복소수를 적절한 형태로 변환해야 한다. 본 논문에서는 복소수를 위상으로 변환하여 CNN에 입력하였다. 그림 1의 특징 추출기 내부 블록의 각 색상은 CNN의 계층(layer)을 의미하며, 각 계층의 블록 폭은 3×3 크기를 갖는 커널(kernel)이 첫 번째 계층부터 순차적으로 16, 32, 64, 128, 256, 512, 1024개 채널의 피처 맵을 형성함을 의미한다. 학습 전 각 계층 커널의 초기화는 He initialization[3] 방식으로 초기화하였다. 또한 공분산 행렬의 모서리 데이터를 충분히 활용하기 위해 padding 1을 적용하였다. CNN의 모든 계층에 배치 정규화(batch normalization)를 수행하였으며, 활성화 함수(activation function)는 relu function을 적용하였다. 추출된 피처 맵을 fully connected layer에 입력하기 위해 1차원 embedding vector로 변환하게 되면 공간적 정보가 소실되는데 공간 정보 소실을 최소화하기 위해 GAP(global average pooling)을 적용하였다. GAP은 각 채널의 global context 정보를 얻을 수 있어 fully connected layer보다 공간 정보 소실이 적게 발생되며, 파라미터를 차지하지 않아 네트워크 연산 속도가 빠르고 과적합(overfitting)을 방지한다는 장점이 있다[4].
가중치 추정기는 3개의 fully connected layer로 구성되어 있으며 각 은닉계층은 각각 1,024, 1,024를 추정하고자 하는 부배열 개수만큼의 노드를 갖는다. CNN과 마찬가지로 배치 정규화를 적용하였으며, 활성화 함수는 relu function, 가중치 초기화는 He initialization 방식을 적용하였다. 다만, 마지막 계층은 이전 계층과 다르게 활성화 함수를 쌍곡 탄젠트(hyperbolic tangent)로 적용하였으며, 제안하는 네트워크가 윈도우 함수(window function)가 적용된 기존 수신 빔패턴을 최대한 유지하면서 재밍 신호 방향으로는 널링을 형성하도록 학습시키기 위해 0으로 가중치를 초기화하였다.
Ⅲ. 데이터셋 구성
네트워크 학습에 필요한 데이터셋의 규모는 네트워크 구조, 학습 방식, 추정 목표, 복잡성 및 데이터의 구성, 품질, 종류, 분포[5] 등 다양한 요인과 경험을 토대로 결정된다[6],[7]. 일반적으로 데이터셋 규모가 클수록 네트워크를 학습시키기에 유리하나, 메모리 등 물리적 한계로 인해 제한되며, 너무 적은 데이터셋이 구축되는 경우 네트워크가 올바르게 학습되지 않는 문제가 발생한다. 이에, 네트워크 학습을 위해 1,000, 5,000, 10,000개의 데이터셋을 구축하여 네트워크 학습을 시도하였으며, 10,000개의 데이터셋의 경우 메모리 한계에 의한 물리적 환경상 이유로 학습이 불가하였고, 1,000개의 데이터셋에서도 네트워크 학습은 이루어졌으나, 5,000개의 데이터셋에서의 네트워크 학습 성능이 더 우수하고 메모리를 최대로 활용할 수 있어 네트워크 학습을 위한 5,000개의 모의 신호 데이터셋을 구축하였다. 네트워크 입력을 위한 신호는 테일러 윈도우 함수(n=5)이 적용된 부배열 단위의 수신 신호로 이루어져 있으며, 표적 및 재밍 신호를 포함한다. 신호 X는 고정된 잡음 크기와 15~80 dB 이내에서 무작위의 신호대 잡음 비율(signal to noise ratio, SNR)과 재밍 대 잡음 비율(jamming to noise ratio, JNR)을 가지며, 레이다 빔, 표적 및 재머는 무작위 방향으로 구성하였다. 신호 대 잡음 비율과 재밍 대 잡음 비율의 범위는 표적 RCS(radar cross section)를 2 m2으로 가정하여 레이다 탐지 성능을 고려해 최소값을 15 dB로[8], 다기능 레이다의 신호처리기의 성능을 고려하여 80 dB로 설정하여 모의하였다[9]. 앞서 언급한 바와 같이 적응형 빔형성 가중치를 추정하기 위해서는 수신 기간 동안 수신 신호를 반복적으로 수집한 학습 훈련 데이터(training data)가 필요한데, 일반적으로 스냅샷(snapshot)을 N=20을 기준으로 수집한 학습 훈련 데이터를 활용한다[10],[11]. 따라서 본 논문에서는 스냅샷을 N~20으로 설정하여 제안한 네트워크 뿐만아니라, LCMV 및 CSC에 입력 신호에도 동일하게 적용하였다.
네트워크 학습을 위한 신호는 네트워크 입력 신호와 특성이 동일한 신호로 이루어져 있으나, 레이다 빔과 같은 방향 θ1에 표적이 존재하는 수신 신호 a(θ1)와 무작위 방향 θ2에 재머가 존재하는 수신 신호 a(θ2)으로 구성하였다. 비지도 학습 방법으로 네트워크를 학습하기 때문에 정답 라벨링이 된 데이터는 포함되지 않았으며, 네트워크가 추정한 결과에 대한 상황을 평가할 수 있는 데이터로만 구성하였다.
Ⅳ. 네트워크 학습 방법
재밍 신호 억제를 위한 최적화된 적응형 빔형성 가중치 W는 재밍 신호가 존재하는 환경에서 식 (1)과 같이 원하는 표적 방향 θ1으로의 수신 신호 a(θ1)는 최대한 보존하면서, 이외 수신 신호 X에 대해서는 식 (2)와 같이 최소화하는 값이다.
표적이 존재하는 주엽 방향의 신호는 최대화하면서 이외 방향의 신호는 최소화하게 되면 식 (3)의 신호대 간섭 및 잡음 비율이 최대화되며, 이를 통해 표적 식별 성능이 향상된다. 따라서 네트워크의 학습 목적은 신호대 간섭 및 잡음 비율을 최대화하는 가중치 벡터(weight vector) w를 찾는 것이다. P1은 표적 반사 신호 전력, P2는 재머 신호 전력, θ2는 재머 방향, σ2은 잡음의 분산을 의미한다.
비지도 학습 기반의 CNN을 활용하여 가중치 벡터 w를 찾아내기 위해 네트워크 loss Lloss를 정의하는 다양한 전략이 있다. 먼저, 식 (3)의 신호대 간섭 및 잡음 비율 자체를 최대화하는 방향으로 학습되도록 Lloss를 정의하는 방법이 있다. 신호대 간섭 및 잡음 비율을 최대화하게 되면 최종적으로 식 (4)와 같이 원하는 표적 신호는 최대한 보존하면서 식 (5)와 같이 재밍 신호는 최소화하는 w를 찾을 수 있게 된다.
따라서 신호대 간섭 및 잡음 비율을 활용하여 비지도 학습을 위한 네트워크 Loss LSINR를 식 (6)과 같이 나타낼 수 있다. n은 mini-batch size를 의미한다.
하지만 LSINR은 원하는 표적 신호와 재밍 신호 간 비율로 표현되기 떄문에 두 신호가 같은 방향으로 변하는 경우 LSINR이 변하지 않게 되어 네트워크 학습이 원활하게 되지 않는 문제가 발생한다. 따라서 본 논문에서는 식 (4)와 식 (5)를 활용하여 네트워크 비지도 학습을 위한 loss Lloss를 식 (7)과 같이 정의하였다.
네트워크 학습을 위한 하이퍼 파라미터는 mini-batch size 4, 학습 비율 lr=10−5로 설정하였으며 Lloss가 5 ephoch 이내에서 감소하지 않는 경우 현재 learning rate의 절반으로 감소하도록 하였다. Optimizer는 Adam optimizer[12]를 적용하였다.
Ⅴ. 학습 결과 및 평가
제안한 네트워크에 대한 빔 패턴 및 성능분석에 u-v 좌표계를 활용하였다. 텍스처(texture) 좌표계라고도 불리는 u-v 좌표계는 사인 공간(sine-space)에서 3차원 방향을 표현하기에 충분한 자유도를 갖고 있으며, 빔 방향에 따라 빔폭이 변하지 않고 일정하므로 빔 패턴 등을 해석하는데 용이하다는 장점이 있다[13]. 재밍 억제 능력을 비교하기 위해 재밍 억제 기술을 적용하지 않은 기존(nominal) 성능과 CSC, LCMV, 제안한 네트워크의 성능을 비교하였다.
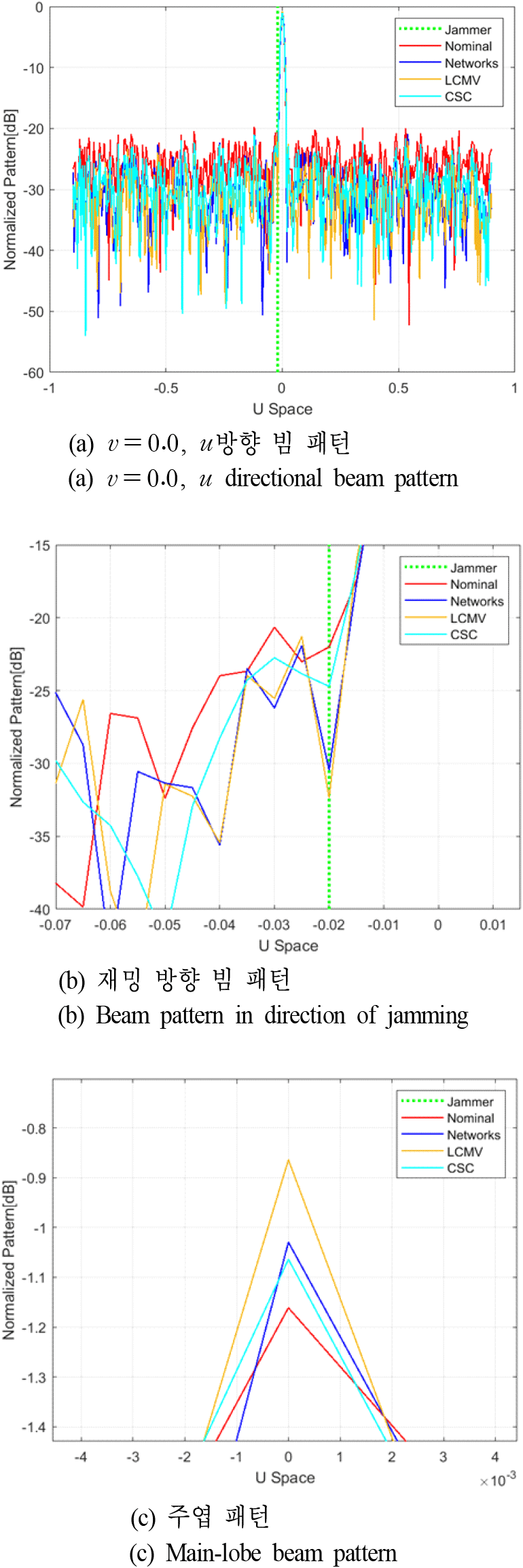
제안한 네트워크가 재밍을 억제하는 빔형성 가중치를 추정하였는지 확인하기 위해 빔 패턴을 분석하였다. 그림 2는 u-v 좌표계 기준으로 주빔 방향 u=0.0, v=0.0 재밍 방향 u=0.02, v=0.0, 신호 대 잡음 비율 30 dB, 재밍 대 잡음 비율 35 dB 환경에서 각 방법에 대한 빔 패턴을 비교한 것으로 그림 2(a)는 u 방향에서의 빔 패턴이며, 그림 2(b)와 그림 2(c)는 그림 2(a)를 재머 방향과 주빔 방향으로 확대한 빔 패턴이다. 그림 2(b)에서 LCMV, CSC, 제안한 네트워크의 빔 패턴을 보면 재밍 방향의 수신 신호가 억제됨을 확인할 수 있으며, LCMV, CSC, 제안한 네트워크 순으로 좋은 재밍 억제 성능을 보이는 것을 정성적으로 확인할 수 있다. 또한, 그림 2(c)에서는 재밍을 억제하면서도 LCMV, CSC, 제안한 네트워크 순으로 표적 신호 수신 성능이 잘 유지됨을 확인할 수 있다. 표 1은 재머 방향과 주엽 방향에서의 정규화된 전력을 비교한 것으로 재밍 방향에서 전력이 작을수록, 주엽 방향에서 전력이 클수록 좋은 성능을 갖는다. 제안한 네트워크는 LCMV보다 재밍 방향 전력은 1.92 dB 높고, 주엽 방향 전력은 0.17 dB 낮았으나, CSC보다는 재밍 방향 전력은 5.74 dB 낮고, 주빔 방향 전력은 0.03 dB 높은 성능을 보여 LCMV보다는 다소 부족하지만 CSC보다 좋은 성능을 보였다.
| Method | Nominal | CSC | LCMV | Proposed networks | |
|---|---|---|---|---|---|
| Jamming direction | Normalized power (dB) | −22.01 | −24.71 | −32.37 | −30.45 |
| Main-lobe direction | −1.16 | −1.06 | −0.86 | −1.03 | |
재밍을 효과적으로 억제하게 되면 신호대 간섭 및 잡음 비율이 높아지게 되고 레이다의 표적 식별 능력이 향상된다. 이에, 제안한 네트워크, LCMV, CSC의 가중치 및 신호대 간섭 및 잡음 비율을 비교하였으며, 결과는 표 2와 같다. 가중치 비교는 제안한 네트워크와 LCMV에 대해 레이다 안테나 중심의 부배열 4×4(16개)를 표본화하여 비교하였다. LCMV와 제안한 네트워크는 가중치 추정에 모든 부배열을 활용하므로 부배열 개수만큼 가중치가 추정되는 반면, CSC의 경우 선택된 일부 부배열만 활용하여 가중치를 추정하므로 선택된 부배열 개수만큼 가중치가 추정된다. 따라서 CSC는 LCMV 및 제안한 네트워크와 가중치 개수가 달라 직접적인 비교가 어려우므로 제외하였다. 또한, 시뮬레이션에 활용한 레이다의 부배열 개수가 많아 안테나 중심에 있는 부배열 4×4를 표본화하여 가중치를 비교하였다. 신호대 간섭 및 잡음 비율을 비교한 결과, LCMV가 30.17 dB로 가장 높은 성능을 나타냈으며 제안한 네트워크가 29.93 dB, CSC가 27.64 dB 순으로 좋은 신호대 간섭 및 잡음 비율 성능을 보였다.
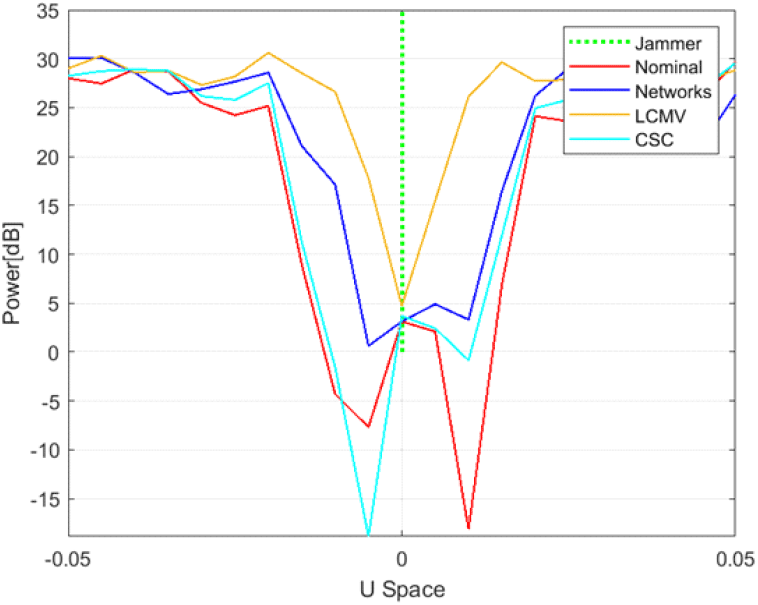
그림 3은 기존과 동일한 환경에서 재머 방향이 u=0.0, v=0.0일 때의 전력 응답(power response)을 비교한 결과로, 전력 응답 그래프가 재밍 방향으로 널링 폭이 좁을수록 재밍에 대한 영향이 적음을 의미한다. 그림 3와 같이 LCMV 널링 폭이 가장 좁았으며, 제안한 네트워크, CSC 순으로 좁은 널링 폭을 보였다. 이를 통해 제안한 네트워크는 LCMV보다 재밍의 영향을 많아 성능이 다소 낮지만, CSC보다는 재밍을 효과적으로 억제하여 재밍 영향을 덜 받음을 알 수 있다.
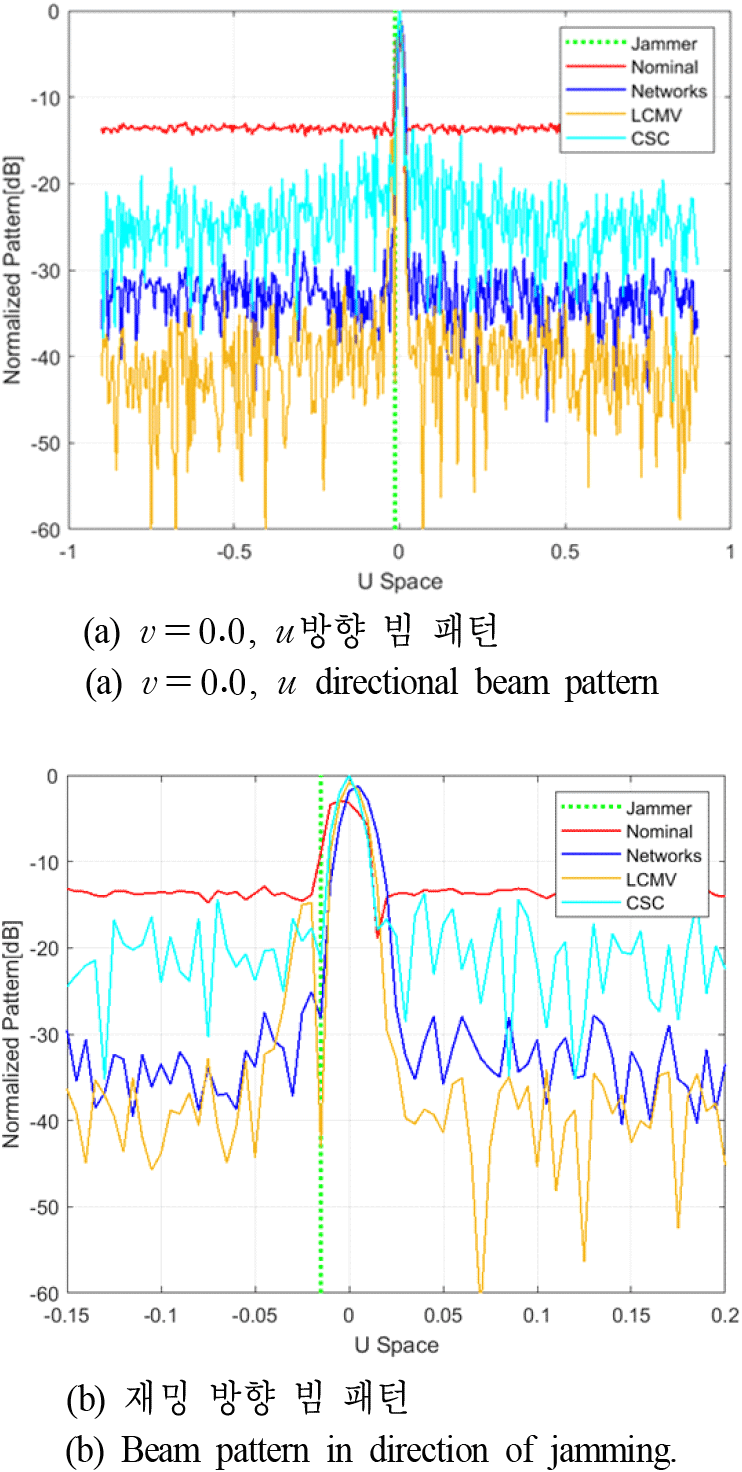
그림 4는 고출력 재밍 상황에서 재밍이 효과적으로 억제되는지를 확인하기 위해 이전 빔 패턴 비교 조건과 동일 조건에서 간섭 대 잡음 비율을 40 dB로 변경하여 고출력 재밍에 의한 기존 안테나 패턴 포화 상황에서의 성능분석을 추가 수행한 결과이다. 그림 4(a)는 u 방향에서의 빔 패턴이며, 그림 4(b)는 재밍 방향으로 확대한 빔 패턴이다. 그림 4와 같이 고출력 재밍 환경에서도 제안한 네트워크와 LCMV는 재밍을 억제하여 안테나 포화가 발생하지 않았으나 CSC는 재밍을 효과적으로 억제하지 못해 전력 레벨이 다소 상승하였다. 이를 통해 제안한 네트워크는 고출력 재밍 환경에서도 CSC보다 재밍을 억제하는 효과가 우수함을 알 수 있다.
각 방법별 적응형 빔형성 가중치를 추정하는데 필요한 소요 시간은 표 3과 같으며, 제안한 네트워크는 LCMV 보다는 빠르기는 하나 CSC보다는 다소 느린 성능을 보여 향후 네트워크 경량화 또는 CSC와 같이 일부 부배열만 활용하여 가중치를 추정하는 등의 방법 등 개선이 필요한 것으로 보인다.
| Method | CSC | LCMV | Proposed networks |
|---|---|---|---|
| Elapsed time (ms) | 0.344 | 83.25 | 53.84 |
Ⅵ. 결 론
본 논문에서는 고출력 재밍 신호를 억제하기 위한 비지도 학습 기반의 CNN 활용 적응형 빔형성 가중치 추정 네트워크를 제안하였다. 제안한 네트워크는 LCMV보다 적응형 빔형성 가중치 추정 속도는 29.41 ms 빠르면서도 CSC보다 신호대 간섭 및 잡음 비율 기준으로 2.3 dB 좋은 재밍 신호 억제 성능을 보였으며, 이를 통해 재밍 억제를 위한 비지도 학습 기반 적응형 빔형성 추정 네트워크의 적용 가능성을 확인하였다. 실시간 처리를 위한 CSC 수준의 처리 속도를 확보하기 위해서는 네트워크에서 불필요한 노드들을 제외시켜 네트워크를 경량화하는 방법과 CSC와 같이 가중치 추정 연산에 필요한 부배열 개수를 선택적으로 줄이는 방법이 있다. 네트워크 경량화 방법은 성능에 영향을 미치기 때문에 성능저하를 최소화하면서도 처리 속도를 개선할 수 있는 방법을 모색해야 하며, 부배열을 선택적으로 줄이는 경우에는 어떤 부배열을 얼마나 많이 선택하여 연산에 반영할지 연구가 필요하다. 향후 실제 환경에서 실시간 처리를 위한 추정 속도 개선과 더불어 재밍 신호 억제 성능 향상, 그리고 단일 수신빔 뿐만 아니라 다중 수신빔에서도 재밍 신호를 효과적으로 억제할 수 있는 네트워크에 대해 추가 연구할 계획이다.