Ⅰ. 서 론
전자파는 서로 다른 굴절률을 갖는 두 매질의 경계면에서 굴절, 반사한다. 지구 대기권은 서로 다른 굴절률을 갖는 여러 층으로 구성되며, 우주에서 대기권을 통과하여 지상에 도달하는 전자파의 전파 특성은 대류권과 성층권의 대기 굴절률에 의해 결정된다[1]. 대기 굴절률은 기온, 기압, 상대습도의 측정값을 통해 정확한 계산이 가능하지만, 전파 특성 예측을 위해 실시간으로 모든 점에서 측정값을 얻는 것은 물리적·시간적 제약 때문에 어려움이 있다. 따라서 일부 지점에서 측정된 값들을 기반으로 한 공간 보간법을 활용하여 굴절률을 예측하는 방법이 사용된다[2]. 공간 보간의 정확도를 높이기 위해 더 다양한 지점에서 측정된 값들이 요구되지만, 국내에서 대기 굴절률 예측에 필요한 기상관측값을 제공하는 기상 관측소의 수는 한정적이다. 이 문제는 현재는 운용되지 않는 기상관측소들의 과거 시점의 측정 데이터를 활용함으로써 해결할 수 있다. 즉, 과거에 운용되던 기상 관측소의 측정값의 시계열 패턴을 학습한 딥러닝 모델을 이용하여 미래 시점의 측정값을 예측함으로써, 공간 보간에 이용 가능한 측정값의 개수를 증가시킬 수 있다. 다양한 분야에서 시계열 데이터와 딥러닝을 이용한 미래 시점의 데이터를 예측하는 연구가 수행되었으나, 이를 대기 굴절률의 예측에 적용한 사례가 없어 이에 대한 연구가 필요하다.
본 논문에서는 과거의 시계열 데이터를 학습하여 미래 시점의 값을 예측하는 딥러닝 모델의 방법론을 제시하고, 경기도 오산의 기상관측소에서 과거의 특정 기간동안 수집된 기상관측데이터와 LSTM(long short-term memory)구조를 갖는 딥러닝 모델을 이용하여 미래 시점의 대기 굴절률을 예측한다.
Ⅱ. 딥러닝 기반의 시계열 예측
본 논문에서 사용된 기상관측데이터는 각 데이터가 일정 시간 간격으로 순차적으로 기록된 시계열 데이터 특성을 갖는다. 이러한 시계열 데이터의 패턴을 학습하기 위해 적합한 딥러닝 모델은 구조는 순환신경망(recurrent neural network, RNN)이며, RNN은 기본적으로 다층 퍼셉트론(multi-layered perceptron, MLP) 구조에서 이전 시간(tn-1)단계의 은닉층 출력을 다음 시간(tn)의 은닉층 입력으로 재사용하는 경로가 추가된 형태로 과거 정보를 기억하는 기능을 갖는다. LSTM은 RNN에 게이트 메커니즘이 추가된 신경망으로, 장기 기억 능력이 강화되고 RNN의 기울기 소실 문제를 완화하여 시계열 데이터의 장기적인 패턴 학습에 적합하다[3]. 이러한 LSTM 신경망의 특성은 수십 년에 걸쳐 누적된 대기 굴절률의 장기적인 패턴 학습에 적합하기에 본 논문에서는 대기 굴절률의 시계열 예측을 위해 LSTM 구조의 신경망을 사용한다.
본 논문에서는 경기도 오산의 기상관측소 상공의 대기 굴절률 예측하기 위하여 경기도 오산에서 1991년 1월 31일 9시부터 2023년 7월 31일 21시까지 12시간 간격으로 측정된 11,942개의 과거의 기상관측데이터를 이용한다. 데이터의 수집을 위해 University of Wyoming의 기상과학과 웹페이지의 데이터베이스를 활용한다[4]. 각 기상관측데이터는 고도에 따른 기온, 기압, 상대습도를 포함하며, 대기 굴절률은 다음과 같은 식에 의해 계산된다[5]. 식 (1)에서 N은 대기 굴절률[N-unit], T는 기온[K], P는 기압[mbar], e는 수증기 부분압력[mbar]을 나타낸다.
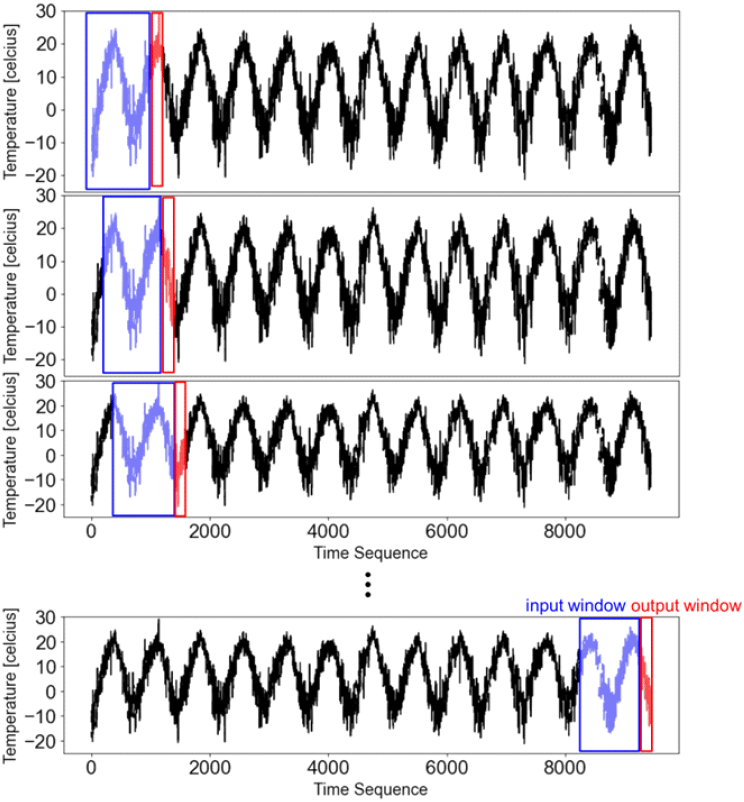
그림 1은 경기도 오산의 기상관측소 상공 1,500 m에서 12시간 간격으로 수집된 기상관측데이터의 시계열 분포를 나타낸다. 시계열 데이터 예측 문제는 그림 1에서 시계열 데이터가 나타내는 데이터의 장기적인 패턴을 LSTM 신경망이 학습할 수 있도록 지도학습 문제로 변형된다[6]. 지도학습 문제를 위한 학습데이터는 수집된 시계열 기상관측데이터로부터 생성된다. 그림 2는 슬라이딩 윈도우 방식을 이용한 학습데이터셋의 생성 과정을 나타낸다. 각 학습데이터는 input window, output window로 구성되며, 슬라이딩 윈도우 방식으로 다수의 학습데이터가 생성된다. 본 논문에서 제안된 LSTM 신경망은 기온, 기압, 상대습도와 같은 변수들의 상관관계를 고려한 다변량 시계열 예측 모델이며, 각 학습데이터는 하나의 input window에 다수의 입력이, 하나의 output window에 다수의 출력이 포함되는 many to many 방식으로 구성된다.

본 논문에서 LSTM 모델 구축을 위해 파이썬 Tensorflow-Keras 라이브러리를 이용하였다. 교차 검증을 위하여 1991년 1월 31일 9시부터 2018년 6월 31일 21시까지 10,722개의 데이터는 훈련 세트, 2018년 7월 1일 9시부터 2023년 7월 31일 21시까지 1,190개의 데이터는 검증 세트, 2023년 8월 1일 9시부터 2023년 8월 30일 9시까지 30개의 데이터는 테스트 세트로 구분된다. 그림 3은 훈련 횟수에 따른 훈련 세트와 검증 세트의 손실함수를 나타낸다. 과적합 또는 과소적합을 방지하기 위해 훈련 횟수는 두 그래프의 교자점인 141회로 결정된다. 예측 성능은 input window의 크기가 20, output window 크기가 4인 경우에 가장 최적의 성능을 보였다. 이에 따라 최적화된 LSTM 신경망은 입력층의 노드가 20개, 출력층의 노드가 4개, 은닉층이 30개인 구조를 갖는다. 즉 신경망은 입력층에서 20개일의 굴절률을 입력값으로 사용하며, 30개의 은닉층(drop out=0.2)을 거쳐 계산된 4개일의 굴절률은 출력층에서 출력된다. 학습에 사용된 옵티마이저는 RMSprop, 손실함수는 MSE(mean squared error)이다. Batch size=32, learning rate=0.001이며 학습은 AMD Ryzen 7 5800X 8-Core Processor 3.80 GHz, 128 GB RAM, NVIDIA GeForce RTX 3070 GPU 환경에서 수행되었다.
그림 4는 2023년 8월 1일 9시부터 2023년 8월 30일 9시까지 경기도 오산의 기상관측소 1,500 m 상공에서 대기 굴절률의 측정값을 최종 선정된 모델의 예측값과 비교한 결과를 나타낸다. 해당 날짜의 대기 굴절률 예측을 위해 1991년 1월 31일 9시부터 2023년 7월 31일 21시까지 12시간 간격으로 측정된 11,942개의 과거의 기상관측데이터로부터 생성된 11,912개의 학습데이터가 사용되었다. 시계열 예측의 평가 지표는 MAPE(mean absolute percentage error)가 사용되었으며, 다음과 같은 식에 의해 계산된다.
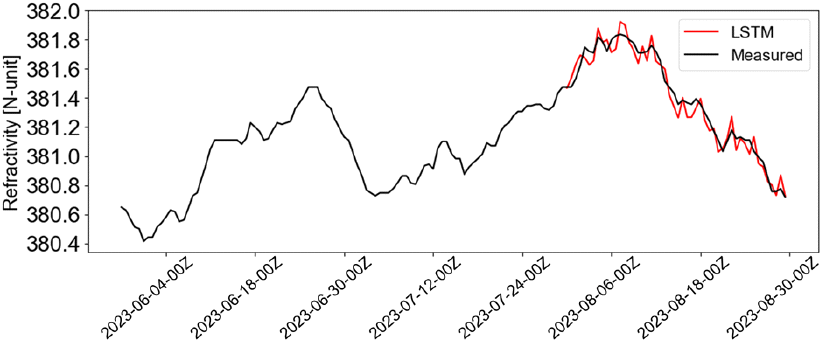
식 (2)에서 Nmeasured는 대기 굴절률의 측정값, Nforecasted는 대기 굴절률의 예측값을 나타낸다. 측정값과 예측값의 MAPE는 3.15 %이며, 대기 굴절률의 시간에 따른 예측값은 측정값과 어느 정도 일치하는 경향을 보인다. 그림 5는 2023년 8월 4일 9시, 2023년 8월 5일 9시에 고도에 따른 대기 굴절률의 측정값을 제안된 모델의 예측값 그리고 통계학 기반의 전통적인 시계열 예측 기법인 ARIMA (autoregressive integrated moving average)[7] 모델과 비교한 결과를 나타낸다. 평균 MAPE는 제안된 모델, ARIMA에서 각각 2.75 %, 7.61 %로, 본 논문에서 제안한 LSTM 기반의 예측모델이 기존의 ARIMA 모델에 비하여 실제 대기 굴절률을 더 잘 예측할 수 있음을 보여준다.

Ⅲ. 결 론
본 논문에서는 과거의 시계열 데이터를 학습하여 미래 시점의 대기 굴절률을 예측하는 LSTM 신경망 기반의 딥러닝 시계열 예측 모델을 제안하였다. 또한 제안된 방법으로 실제 경기도 오산의 기상관측소에서의 시간에 따른 미래 시점의 대기 굴절률과 특정 날짜의 고도에 따른 대기 굴절률을 예측하였다. 예측 결과, 제안된 모델이 대기 굴절률 예측에 있어 ARIMA에 비해 유의미한 결과를 제공할 수 있음을 확인하였다. 이렇게 예측된 대기 굴절률은 미래 시점의 대기 굴절률을 예측할 수 있을 뿐만 아니라, 과거의 대기 굴절률도 예측함으로써 공간 보간법에 사용되는 딥러닝 모델의 학습데이터로 사용될 수 있으며, 실제 대기의 굴절률에 가깝게 더 정교하게 예측된 대기 굴절률은 측정 오차를 보정하고, 설계 마진을 확보함으로써 레이다 및 위성 통신 시스템의 성능 개선과 최적화에 도움이 될 수 있다.

