Ⅰ. 서 론
전자전에서 주요한 역할을 하는 레이다(radar)는 전파를 사용하여 특정 목표물까지 거리와 방향, 목표물 크기, 이동 속도 등을 측정하는 전자장치이다[1]. 미사일이나 유도탄 공격 시 목표물을 탐색하거나 추적하기 위해서는 대부분 레이다를 사용한다. 이러한 전자전 환경에서 회피나 전파 방해 등의 방법으로 적시에 대응하기 위해서는 적 레이다 신호를 빠르게 탐지해야 한다.
한편, 레이다 신호는 보통 약 20 GHz까지 넓은 대역 내에 존재한다[2]. 따라서 전체 대역을 몇 개의 부대역으로 나누어 순차적으로 탐색하거나, 또는 부대역을 동시에 병렬 탐색하는 방법으로 전체 대역을 탐색한다. 이때 부대역이 넓을수록 탐색 시간을 줄일 수 있다. 따라서 전자전과 같은 시급한 환경에서는 광대역 신호를 실시간으로 탐지할 수 있는 고속 탐색기가 필요하다.
신호 탐색을 위해서는 주로 스펙트럼 탐색기(또는 스펙트럼 분석기라 부름)를 사용한다. 스펙트럼 탐색기는 신호의 스펙트럼을 구하여 표시(display)하는 장치를 말한다[3]. 가로축에 측정 가능 범위의 주파수를 나타내고, 세로축에 주파수 크기를 나타낸다. 신호 존재 여부를 판단하고, 신호가 존재하는 주파수대를 추정한다. 스펙트럼을 구하는 방법은 크게 스윕 분석 방법(swept spectrum analyzer)과 벡터 신호 분석(vector signal analyzer) 방법이 있다[4],[5]. 스윕 방법은 아날로그 방식부터 전통적으로 사용하던 방식으로, 주파수가 시간적으로 점차 증가(sweep)하는 국부발진기(local oscillator)를 사용한다. 스윕 주파수로 입력 신호를 동조(tuning)시켜 하향 변환(down conversion)한 다음, 정해진 분해능 대역폭(resolution bandwidth)을 가진 저역 필터를 통과시켜 동조 주파수의 전력을 측정하는 방식이다. 이 방법은 국부발진기의 스윕 주파수 범위만큼 넓은 대역을 탐색할 수 있지만, 시간적으로 어느 한 순간에는 특정 주파수대의 신호만 검출할 수 있다. 결과적으로 주파수 특성이 시간적으로 변화가 없는 정적(static) 신호에는 적합하지만, 시간적으로 변화가 있는 신호의 스펙트럼은 측정이 누락될 가능성이 크다.
벡터 신호 분석 방법에서는 먼저 입력 신호를 RF (radio frequency) 대역 또는 IF(intermediate frequency) 대역에서 AD(analog-to-digital) 변환하고, 디지털 처리를 통해 기저대역으로의 하향 변환과 필터링을 한다. 기저대역 신호는 FFT(fast Fourier transform)를 통해 주파수 영역으로 변환한 다음 각 주파수의 진폭과 위상을 계산한다. 입력 신호를 일단 메모리에 저장한 다음 FFT 구간 단위로 읽어서 스펙트럼을 계산하기 때문에, FFT 속도가 데이터 저장 속도에 비해 더 빠르지 않으면 구간 사이의 데이터 누락이 발생한다.
실시간 스펙트럼 분석(real-time spectrum analysis)이란 신호의 시간적인 누락없이 전체 신호에 대해 스펙트럼을 표시하는 것을 말한다[3]. 신호 탐색을 목적으로 하는 스펙트럼 분석기는 진폭 스펙트럼만 필요하며, 스펙트럼은 레이다 신호를 디지털 신호로 AD 변환하고, FFT를 계산함으로써 구한다. 이렇게 구한 스펙트럼을 운영자가 모니터를 통해 볼 수 있도록 일정 시간 동안 누적해서 전달한다.
이 논문에서는 1 GHz 대역폭 내에 존재하는 레이다 펄스 신호를 실시간으로 탐지할 수 있는 디지털 스펙트럼 탐색기(분석기)를 설계하고 그 구현 방법을 제시한다. 탐색 대역폭은 출시된 AD 변환기의 표본화 주파수, 디지털 회로의 처리 속도 등에 의해 결정된다. 대역폭이 1 GHz인 연속 신호에 대해 실시간으로 스펙트럼을 계산하기 위해서는 2 GHz 이상의 표본화 주파수를 가진 AD 변환기뿐만 아니라, 고속의 디지털 처리기가 필요하기 때문에 출시된 하드웨어에 일반적인 방법을 적용해서는 구현하기가 매우 어렵다. 그러나 레이다 펄스 신호는 펄스가 존재하는 시간(펄스 폭)이 펄스가 반복적으로 나타나는 주기에 비해 최대 수 분의 1 정도로 매우 작다[6]. 이 특성을 이용하면 펄스 신호를 누락하지 않고 스펙트럼을 구할 수 있다. 이 논문에서는 또 실시간 스펙트럼 탐색이 가능한 필요조건을 제시한다. 스펙트럼 계산 즉 FFT 계산은 FFT 크기 및 하드웨어에서의 클럭 속도에 의해 처리 속도가 결정되므로, 표본율(sample rate), 펄스 폭(PW: pulse width)과 펄스 반복 주기(PRI: pulse repetition interval)의 비율에 따라 실시간 처리 여부가 결정된다.
이 조건을 바탕으로 설계한 스펙트럼 탐색기는 입력 신호를 고속 AD 변환기를 통해 디지털로 변환하고 펄스 신호의 특성을 반영하여 FFT를 수행함으로써 신호의 스펙트럼을 실시간으로 탐지할 수 있다. 탐색기는 Xilinx사의 RFSoC 평가 키트[7]를 사용하여 구현하고, 그 성능을 살펴본다.
이 논문의 구성은 II장에서 실시간 스펙트럼 탐색기를 설계하고, 실시간 처리가 가능한 필요조건을 제시한다. III장에서는 평가 키트를 사용하여 설계한 탐색기를 구현하고 성능을 살펴본다. 마지막으로 IV장에서 결론을 맺는다.
Ⅱ. 실시간 스펙트럼 탐색기 설계
스펙트럼 탐색기는 그림 1과 같이 크게 레이다 신호를 수신하여 원하는 대역의 스펙트럼을 중간주파수(IF: intermediate frequency)로 이동시켜 출력하는 RF 처리기와 디지털 신호 처리기로 구성되며, 디지털 처리기는 세부적으로 아날로그-디지털 변환(ADC: analog-to-digital convertsion), 디지털 하향 변환(DDC: digital down conversion) 및 표본줄임(down-sampling), FFT를 수행한다.
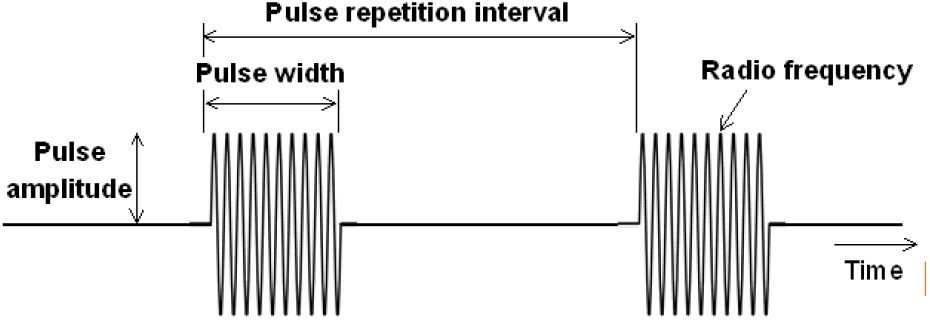
이 논문에서는 펄스 레이다에서 사용하는 펄스 신호를 고려한다. 시간 영역에서 본 펄스 신호의 파형은 그림 2와 같이 높은 주파수의 정현파를 펄스열로 변조하여 포락선이 펄스 형태를 가지게 된다. 펄스 신호를 특징짓는 주요 변수로는 무선 주파수(RF)와 펄스 반복 간격(PRI), 펄스 폭(pulse width: PW)이 있으며, 그 외 펄스 진폭(pulse amplitude: PA), 펄스 내 무선 주파수 변조 형태인 FMOP (frequency modulation on pulses), PMOP(phase modulation on pulses) 등이 있다. PRI와 RF는 시간에 따라 펄스 간에 변하기도 하며, 레이다를 특징짓는 주요 특성이다.
이 논문에서는 PDW(pulse discription word) 생성과 정밀한 신호분석을 위한 준비 작업으로 정해진 대역폭 내의 스펙트럼을 관측하여 펄스 신호가 존재하는 주파수를 측정하는 스펙트럼 탐색기를 설계하는 것이 목적이다. 즉 펄스 신호의 RF 주파수를 찾아내는 것이다.
RF 처리기는 20 GHz 이하의 레이다 신호를 수신하여 IF 대역으로 하향 변환한 다음 출력시키는 역할을 한다. 이때 IF 신호의 대역폭은 광대역을 탐색할 수 있도록 1 GHz로 설계했으며, 그 주파수 대역 위치는 가변적으로 지정할 수 있다. IF 신호는 식 (1)과 같이 나타낼 수 있다.
여기서 p(t) 는 펄스 신호를 나타내며, fIF0 는 IF 주파수로 표본화 주파수를 고려하여 설정한다. ϕ 는 초기 위상을 나타낸다.
IF 신호는 디지털로 처리하기 위해 먼저 AD 변환기를 통해 디지털로 변환된다. AD 변환기의 출력은 식 (2)와 같이 표현할 수 있다.
여기서 n은 시각 t = nTs0 에서의 신호를 나타내며, Ts0 는 표본 간격으로 표본화 주파수가 fs0 일 때 Ts0 = 1/fs0 이다.
표본화에 의해 IF 대역에 위치하던 아날로그 신호의 스펙트럼이 표본화 주파수만큼 이동되어 반복적으로 나타나게 된다. 표본화 주파수는 통과대역 표본화 정리에 따라, 대역폭의 2배 이상 조건을 만족하면서 반복 스펙트럼(alias)이 서로 겹치지 않도록 낮은 값으로 설정할 필요가 있다[8]. 또, IF 신호의 대역폭과 차후 DDC 다음 단계에 위치하는 저역필터의 특성도 고려해야 한다. 주어진 IF 주파수에 대해 AD 변환 후 위치하는 스펙트럼의 간격, 즉 보호 대역폭이 서로 비슷할 때 필터 설계가 용이하게 된다.
DDC는 기저대역에 가장 가까이 위치한 스펙트럼의 중심주파수(fIF 라 놓자)를 0으로 옮기는 역할을 한다. 일반적으로 fIF 와 표본화 주파수가 식 (3)의 관계에 놓이도록 설정한다[9].
이 경우, 그림 3과 같이 스펙트럼을 이동시키기 위해 입력 신호에 를 곱하는 디지털 처리 과정이 단순하게 (j)n 을 곱하는 것이 된다. 즉 실수부와 허수부에 번갈아 +1과 −1을 곱하는 과정이 된다. DDC를 통해 실신호 입력은 복소신호 출력이 되고, 다음 단계에서 실계수를 가지는 저역필터를 통해 기저대역 스펙트럼만 남게 된다.
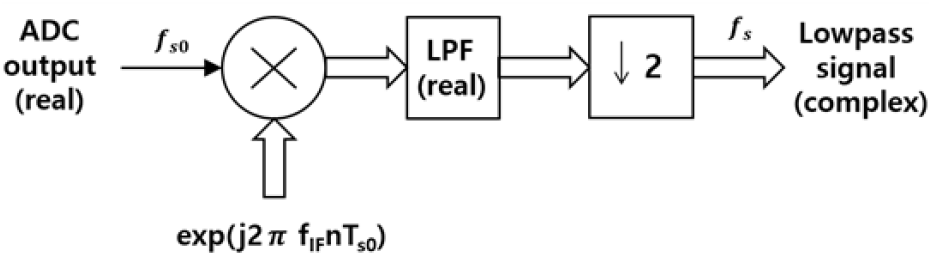
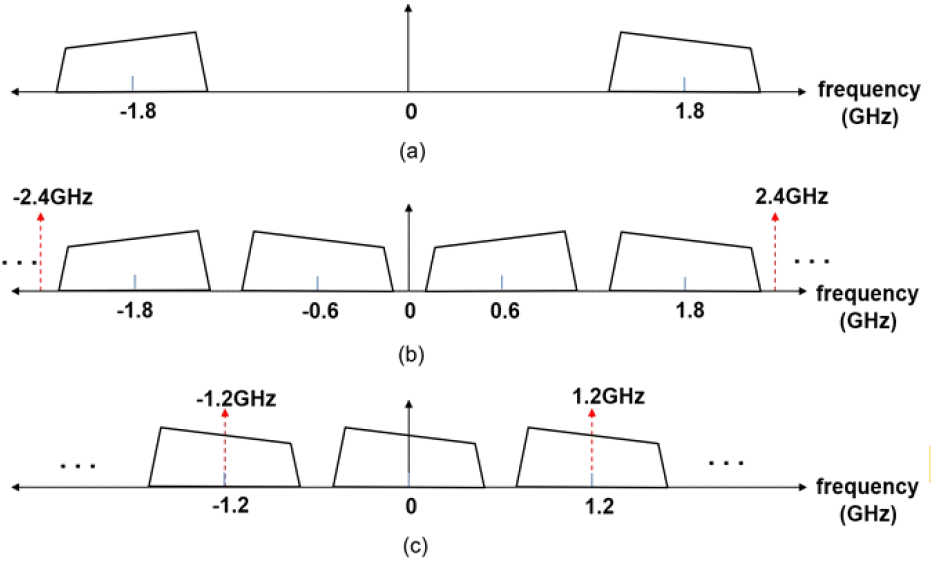
그림 4는 설계에서 설정한 대역폭 B =1 GHz, IF 주파수 fIF0 =1.8 GHz, 표본화 주파수 fs0 = 2.4 GHz일 때 각 단계의 스펙트럼을 나타낸다. 2.4 GHz로 표본화하면 중심주파수가 1.8 GHz에 있던 IF 신호의 스펙트럼이 2.4 GHz마다 반복되므로 스펙트럼이 그림 4(b)와 같이 된다. 이때 DDC 후 인접한 스펙트럼을 차단시키기 위한 저역필터(lowpass filter: LPF)의 최대 롤오프율(roll-off factor)은 20 %가 된다. 마지막으로 LPF 출력을 2:1 표본줄임(down-sampling)하면 표본율은 fs=1.2 GHz가 되고, 그림 4(c)와 같이 스펙트럼이 위치하게 된다.
신호의 스펙트럼은 N-점 FFT를 통해 계산한다. FFT 결과는 첫 번째 및 두 번째 Nyquist 영역에서 계산되므로, 두 번째 영역은 첫 번째 음의 영역으로 환산한다. 두 신호를 구별할 수 있는 최소 주파수 간격인 주파수 해상도는 그림 5로부터 식 (4)와 같이 된다.
설계에서는 N=2,048로 놓았으며, 이 경우 주파수 해상도는 약 586 kHz가 된다.
실시간으로 스펙트럼을 탐색하기 위해서는 AD 변환기 출력 신호에 대해 빠짐없이 스펙트럼을 구해야 한다. 신호의 스펙트럼을 구하는 일반적인 방법에서는 그림 6(a)와 같이 시간 영역에서 신호를 N개 단위의 블록으로 나누어 각 블록의 FFT를 계산한다. 그 다음 각 블록의 진폭 스펙트럼을 일정 개수의 블록에 대해 누적하여 평균 진폭 스펙트럼을 계산하고, 그 결과를 모니터에 표시한다. 평균을 취하는 시간 구간(프레임이라 부르고 Tf 라 놓자)은 사람이 눈으로 스펙트럼을 확인하는 데 무리가 없도록 결정한다. 신호 탐색이 광대역에서 이루어지는 경우, AD 변환 주파수가 높기 때문에 실시간 탐색을 위해서는 매우 고속의 디지털 처리기가 필요하다. 결과적으로 상용 제품으로 출시되는 FPGA(field programmable gate array)에 구현이 어려울 수 있다.
예를 들어 표본율 1.2 GHz, FFT 크기 N =2,048, 프레임 Tf =20 ms라 가정할 때, 표본 수는 약 2.4×107이 되고, 프레임당 스펙트럼을 구하기 위한 FFT 계산 횟수는 약 1,171회가 된다.
레이다 펄스 신호는 일반적인 연속 신호와 다르게 시간 영역에서 신호가 존재하는 구간보다 존재하지 않는 구간이 훨씬 더 크다. 즉, 듀티 비(duty cycle)가 1보다 매우 작다[6]. 따라서 일반적인 스펙트럼 탐색 기법을 펄스 신호에 적용하면 데이터가 없는 부분을 포함하게 되어 시스템이 매우 비효율적으로 동작하게 되고, 하드웨어 속도가 느린 경우 데이터 누락이 발생할 수도 있다. 한편, 데이터가 없는 부분은 주파수 성분에 대한 정보가 없으므로 이 부분을 제외해도 스펙트럼 모양은 같다.
제시한 설계에서는 그림 6(b)와 같이 레이다 펄스 신호의 데이터 부분(즉 펄스 부분)만을 모아 스펙트럼을 계산한다. 연속적으로 유입되는 이산 신호에 대해 미리 설정한 임계치보다 큰 값이 일정 개수 이상 지속되는 경우를 데이터로 고려한다. 펄스 부분만 모으는 과정에서 위상의 불일치가 발생하여 위상 스펙트럼에는 영향을 크게 미칠 수 있다. 그러나 신호 탐지를 목적으로 계산하는 진폭 스펙트럼에는 그 영향이 크지 않음을 실험적으로 확인하였다.
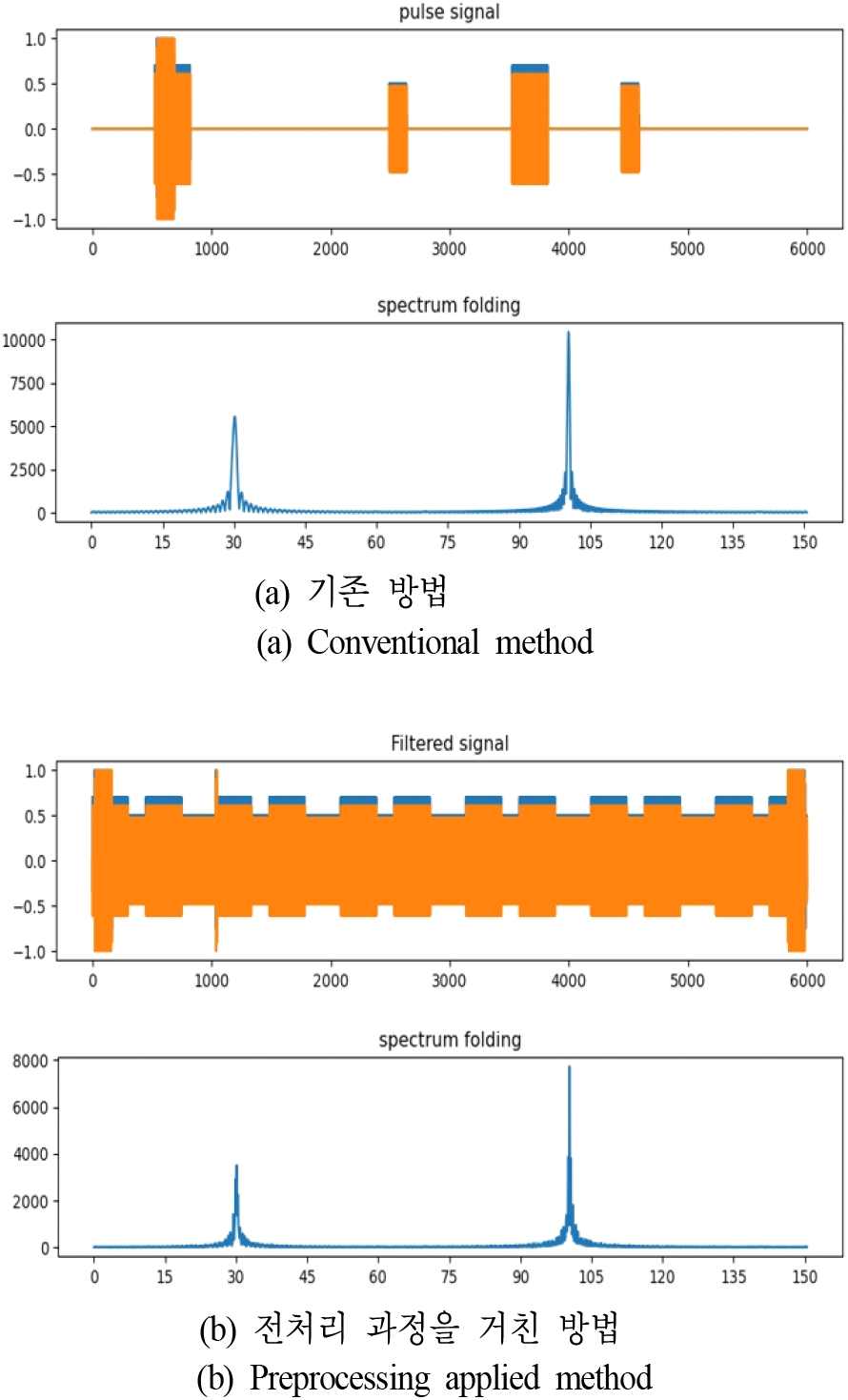
그림 7은 펄스 신호의 전체 구간을 빠짐없이 N 점 FFT를 수행하여 스펙트럼을 구한 경우와, 동일한 신호에 대해 데이터 부분만을 모아 스펙트럼을 구한 모의실험 예를 나타낸다. 신호는 펄스 폭이 2 us이고, 듀티 비가 각각 10 %, 7.7 %인 서로 다른 주파수를 가지는 2개 레이다 신호로 구성되어 있다. 이 경우, 프레임 당 FFT 계산 횟수는 198회로 약 1/6로 감소한다. 그림에서 보면 입력한 주파수 외 다른 부분에서는 뚜렷한 스펙트럼이 나타나지 않는다. 즉 위상 불일치의 영향이 크게 나타나지 않음을 확인할 수 있다.
스펙트럼을 구하는 하드웨어 세부 구조는 그림 8과 같다. 스펙트럼이 기저대역에 위치하는 표본줄임기 출력은 I(inphase) 및 Q(quadrature) 성분으로 구성된 복소신호이다.
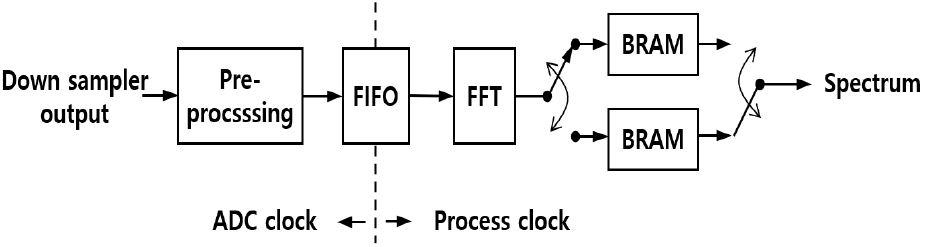
전처리부에서는 I, Q 성분을 입력으로 받아 임계치 이상의 펄스 부분 데이터만 FIFO(first input first output)에 저장한다. FIFO는 스펙트럼 계산부와 입력의 데이터 생성 속도 차이를 해소하는 역할을 한다.
FFT부에서는 데이터를 N개씩 읽어서 FFT를 수행하고, 진폭 스펙트럼을 구하여 스펙트럼 누적기(accumulator)에 누적하여 저장한다. 스펙트럼 누적기는 N개의 데이터를 저장할 수 있는 2개의 블록 메모리(BRAM)로 구현된다. 한 개 프레임 시간이 지나면 다른 블록 메모리로 전환하여 FFT 결과 데이터를 연이어서 저장한다. 한 블록 메모리에 저장된 스펙트럼을 표시기로 전송하는 동안 동시에 계산되고 있는 스펙트럼을 다른 블록 메모리에 누적하도록 구현함으로써 데이터 누락을 방지할 수 있다.
전처리기는 AD 변환 속도인 fs0 에 맞춰 하드웨어가 동작한다. 스펙트럼 계산부는 fs0 보다 작은 별도의 프로세스 클록(Pclk)을 사용한다. 이것은 fs0 가 GHz 단위로 동작할 때, 한 클록에 여러 개를 처리하는 프로세스 클럭으로 사용하기에는 너무 빠른 속도이기 때문이다.
스펙트럼 계산 동작은 FFT부로 데이터를 가져오고, FFT를 계산하고, 계산 결과를 BRAM(block random access memory)에 누적하는 세 단계로 분해할 수 있다. 이 세 단계는 그림 9와 같이 순차 처리와 파이프라인(pipeline) 처리 등 두 가지 방법으로 구현할 수 있다.
순차 처리는 각 단계를 차례대로 수행시키는 방법이고, 파이프라인 처리는 각 단계를 병렬적으로 처리하는 방법이다. 파이프라인 처리는 처리 시간이 가장 긴 단계를 기준으로 그 시간마다 새로운 데이터에 대하여 스펙트럼 계산을 시작할 수 있다. 따라서 파이프라인 처리를 통해 처리 시간이 가장 긴 단계의 시간 내에 N개 이하의 데이터가 입력되면 실시간 처리가 가능하게 된다.
실시간 처리 조건은 데이터 생성 속도, FFT 계산 시간, 스펙트럼 누적 시간 등에 의해 결정된다. 이제 스펙트럼을 구하는 과정에 소요되는 시간을 세부적으로 분석하여 실시간 처리 요건을 만족하기 위한 필요 조건을 도출하고자 한다. 단 FIFO 크기 제한때문에 발생하는 넘침(overflow)은 없다고 가정한다.
펄스 레이다 신호의 듀티비를 D 라 하면 N개의 데이터를 생성하는 평균 시간 Tin 은 식 (5)과 같이 된다.
최종 모니터 표시용 스펙트럼을 계산하기 위해 스펙트럼을 누적하는 동작은 메모리 읽기, 누적 계산, 메모리 쓰기 등 3개 동작을 포함한다. 즉, 1개 데이터마다 메모리를 두 번 접속(access)해야 한다. 스펙트럼을 저장하는 BRAM은 한 개의 Pclk 동안 한 번 읽기 또는 쓰기 동작을 수행할 수 있다. 따라서 스펙트럼 누적 계산에 필요한 시간 Tacc 는 식 (6)과 같이 표현할 수 있다.
여기서 fclk 는 클록 주파수를 나타낸다.
파이프라인 구조에서 N개 데이터 처리 시간은 FFT 계산 시간 Tfft 와 Tacc 중에서 더 긴 것에 의해 결정된다. 일반적으로 FFT 계산은 여러 분야에서 널리 사용되기 때문에 하드웨어 업체에서 제공하는 FFT 블록은 하드웨어적으로 최적화되어 있다. 따라서 Tfft < Tacc 라 가정할 수 있다. 실시간 스펙트럼 탐색 필요 조건은 데이터 생성 시간보다 처리 시간이 짧아야 한다. 즉, Tacc < Tin 를 만족해야 한다. 따라서 식 (5) 및 식 (6)으로부터 식 (7)과 같은 조건을 얻을 수 있다.
실시간 처리 조건은 FFT 크기 N과 무관하며, 프로세스 클록 주파수, 표본율, 듀티비에 의해 결정된다.
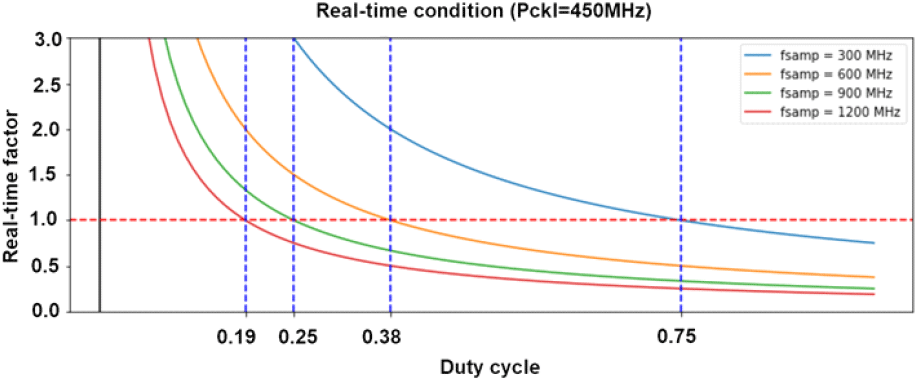
그림 10은 fclk =450 MHz일 때 표본율과 듀티비에 따른 η 값을 나타낸 것이다. 그림에서 η > 1 인 영역이 실시간 스펙트럼 탐색이 가능한 조건을 나타낸다. 그림으로부터 클록 주파수가 fclk = 450 MHz, 표본율 fs =1.2 GHz일 때, 듀티비가 약 19 % 이하면 실시간 스펙트럼 탐색이 가능한 것을 알 수 있다.
Ⅲ. 실시간 스펙트럼 탐색기 구현 및 결과
설계한 스펙트럼 탐색기는 Xilinx 개발 도구 Vitis HLS와 Vivado를 사용하여 프로그래밍한 후 Xilinx 평가 키트 RFSoC ZCU-208에 구현하였다. ZCU-208은 14비트 AD 변환이 가능한 8개의 입력 채널을 가지고 있고, 최대 표본화 주파수는 5 GHz이다. 이 키트를 선택한 이유는 대역폭 1 GHz인 IF 대역 신호를 처리하기 위해서 최소 2 GHz 이상의 표본화 주파수가 필요하기 때문이다. 제시한 탐색기의 AD 변화 주파수는 fs0=2.4 GHz, 표본 줄임율은 1/2, FFT 데이터의 표본율은 fs=1.2 GHz, 클록 주파수는 fclk =450 MHz, FFT 크기는 N=2,048이다. 데이터 전처리부(pre_proc)와 스펙트럼 누적 계산부(acc_spec)는 Vitis HLS로 구현하고, 나머지 구성 요소는 Xilinx 제공 IP(intellectual property)를 사용하여 구현하였다[10],[11].
두 모듈의 합성 결과는 표 1과 같다. 전처리 모듈은 표본 줄임기 출력 데이터에 대하여 계속적으로 동작하고, 전처리에 필요한 클록 수는 4, 데이터가 입력되는 클록 간격(iteration interval)은 1이다. 즉, 처리 시간은 4 클록이 걸리지만 파이프라인 구조로 계산하기 때문에 데이터가 매 클록마다 전처리 블록으로 입력됨을 의미한다. 스펙트럼 누적 모듈은 2,048점 FFT 출력 데이터에 대하여 동작하고, 초기 파이프라인 지연을 포함하여 4,104클록에 스펙트럼 누적을 완료한다. 2,048개 데이터 입력 간격은 2클록이다.
| IP | Latency (CLK) | Iteration interval (CLK) | Pipelined |
|---|---|---|---|
| pre_proc | 4 | 1 | Yes |
| acc_spec | 4,104 | 2 | Yes |
그림 11은 개발한 스펙트럼 탐색기 시험 시스템을 나타낸다. 시험 시스템은 프로그램을 FPGA에 올리기 위한 노트북, 레이다 펄스를 발생시키는 신호발생기, FPGA로 구현한 디지털 처리기 및 결과를 나타내는 표시기로 구성되어 있다. 시험 시스템은 실시간 처리 여부, 디지털 처리 알고리듬의 정확성, 주파수 측정의 정확도 등을 시험하기 위한 것으로, 신호발생기 대신 안테나 및 RF 처리기를 연결하면 실제 수신되는 레이다 펄스 신호를 처리할 수 있다.
그림 12는 구현한 하드웨어 스펙트럼 탐색기가 스펙트럼 계산 각 단계를 순차적으로 처리하는 버스트 모드와 파이프라인 모드에서 동작할 때 각각의 타이밍도(timing diagram)를 나타낸다. 그림에서 TLAST는 마지막 입력 데이터의 계산이 끝난 순간, 즉 FFT 최종 출력이 나오는 순간을 나타낸다. BRAM address는 BRAM 주소를 십진수로 나타낸 것이고, BRAM data는 해당 주소의 데이터값을 나타낸다. 그림은 1개 주소에만, 즉 1개 스펙트럼 성분만 있음을 나타낸다.
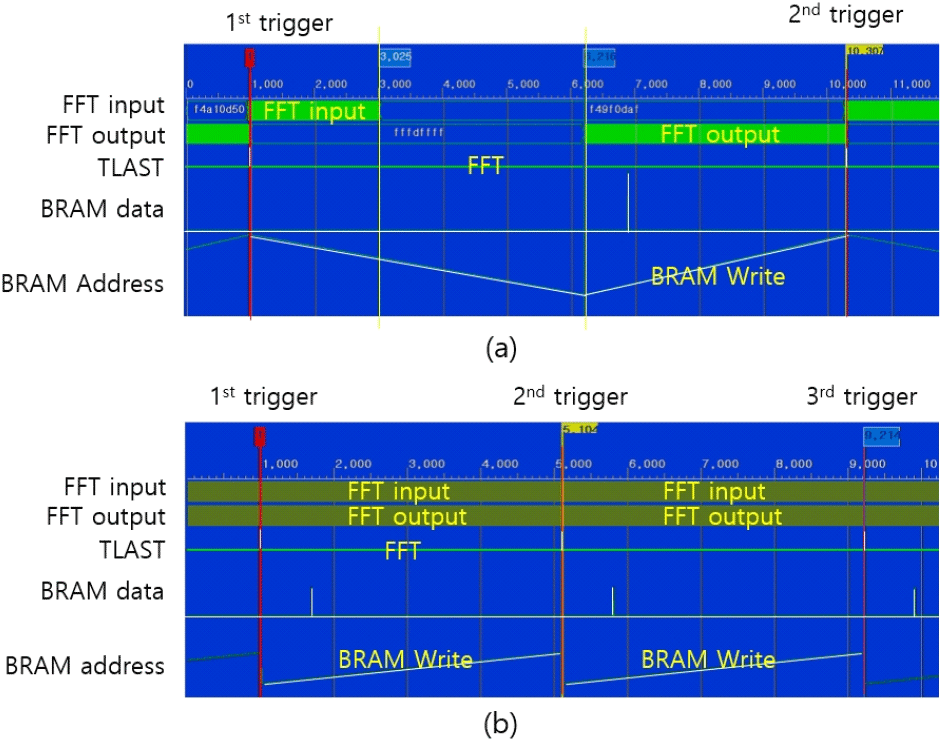
그림 12(a)의 순차 처리 모드에서는 첫 TLAST부터 두 번째 TLAST까지의 시간 동안 2,048개 데이터에 대해 입력, FFT 계산, BRAM에 누적 등의 구간에 해당한다. 입력 시간 동안(FFT input) TLAST 직전부터 3,025번째 클록까지 클록마다 하나씩 2,048개 데이터가 입력된다. FFT 계산은 클록 3,025∼6,126구간에서 이루어진다. 구간 폭은 3,101클록이고, FFT 구간(N)의 2배인 4,096보다 작다. 이로부터 Ⅱ장에서 가정한 Tfft < Tacc 요건을 만족함을 확인할 수 있다. 데이터 출력(FFT output)은 FFT 계산 결과가 출력되는 구간으로 6,126∼10,307클록을 나타낸다. 구간 폭은 2 N보다 약간 큰 4,181클록으로, 스펙트럼 계산 단계에서 가장 긴 시간이 필요하다. 전체적으로 입출력 시 겹치는 구간을 제외하면 10,307클록이 필요하다.
그림 12(b)의 파이프라인 모드에서는 데이터 입력, FFT 계산, 결과 출력이 동시에 수행되는 것을 확인할 수 있다. TLAST 사이 간격은 4,104클럭으로 표 1에서 제시한 IP 모듈 합성 결과와 일치한다. 파이프라인 모드에서는 3개 동작을 수행하는데 필요한 클록 수가 4,104로 순차 모드와 비교하여 약 40 % 소요된다. 식 (7) 및 그림 10에서 제시한 바와 같이 파이프라인 모드에서는 듀티비가 19 % 이하면 항상 실시간 처리가 가능하게 된다. 통상적인 펄스 레이다의 듀티비가 0.1∼20 %[6]인 것을 고려하면 대부분의 레이다 펄스 신호를 실시간으로 처리할 수 있다.
Ⅳ. 결 론
이 논문에서는 레이다 펄스 신호의 스펙트럼을 실시간으로 탐지할 수 있는 고속 스펙트럼 탐색기를 설계하고, 상용 평가 키트에 구현하여 동작성을 검증하였다. 또 실시간 스펙트럼 탐색이 가능한 조건을 표본율, 클록 주파수 및 듀티비 관점에서 제시하였다. 제시한 설계 조건인 표본율 1.2 GHz, 클록 주파수 450 MHz에서 듀티비가 19 % 이하면 실시간 탐색이 가능하다. 또 구현된 탐색기는 1 GHz 대역폭 구간에서 주파수 분해능 약 586 kHz로 고속 스펙트럼 탐색이 가능하다. 따라서 제시한 방법을 적용하면 데이터 누락 없이 레이다 신호의 실시간 탐색이 가능하기 때문에 PDW 생성, 재밍 기법 결정 등 위협 레이다에 대한 더 신속하고 정밀한 대응이 가능할 것으로 기대된다.










