간섭계 레이다 고도계에서 안테나 기준선의 각도 모호성 분석

간섭계는 원래 빛의 간섭 현상을 이용하여 변위를 측정하는 광학계를 의미한다. 간섭계 원리는 경로의 길이가 같은 기준광과 신호광에 대해, 측정 점의 변화로 신호광의 경로가 변화하면 경로차가 발생하고, 간섭을 일으키게 되어 이로부터 원하는 정보를 산출하는 것이다. 위상비교 모노펄스 알고리즘은 간섭계 원리에서 착안하여 표적 각도(방위각 정보)를 추정한다.

그림 1과 같이 단일 기준선에 배치된 2개의 안테나 Ant1, Ant2로 식 (1)의 표적반사신호 S_r이 수신된다고 하면 각 안테나에서의 수신신호 위상은 각각 ϕ₁, ϕ₂가 된다. 이 때 A_r은 수신전력이며, f_c는 송신주파수, τ는 표적반사신호가 수신될 때까지의 지연시간, k는 주파수 변조신호의 시간대주파수 기울기, ϕ는 초기위상이다.

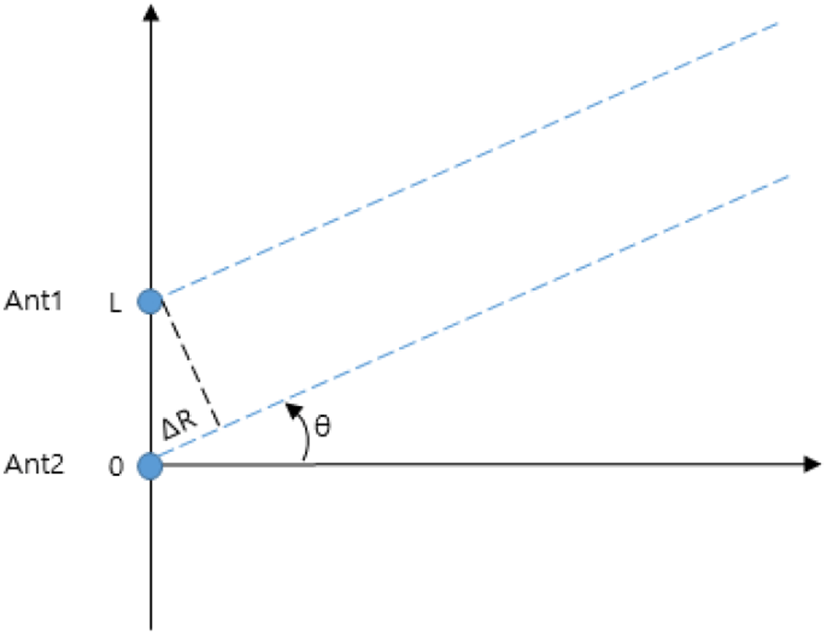
이 때 측정값 ϕ₁, ϕ₂는 수신신호의 Inphase 성분 I와 Quadrature 성분 Q의 비로부터 구할 수 있으므로, 측정 위상차 Δϕ는 식 (2)와 같이 구할 수 있다.

한편, 추정 위상차 Δψ는 그림 1의 경로차 ΔR로부터 식 (3)과 같이 구할 수 있다. 이 때 L은 단일 기준선 간격, θ는 표적 각도, λ는 파장을 나타낸다.

그런데 식 (2)에서 측정 위상차 Δϕ은 주기성이 있어 위상 주기 2 π마다 위상 모호성이 발생한다.^[11] 따라서 식 (2)와 식 (3)으로부터 Δϕ와 Δψ는 식 (4)와 같은 관계를 갖는다. 이 때 n은 주기성을 나타내기 위한 정수값이다.

식 (4)로부터 식 (5)와 같이 표적 각도를 추정한다.

위 식에서 위상 주기 2 π에 따른 각도 모호성을 회피하기 위해서는 $\left|\Delta \psi \right|=\left|\frac{2\pi L\sin \theta }{\lambda }\right|\le \pi$ 를 만족해야 한다. 이 때 L이 λ/2 이하를 만족하면 $\left|\theta \right|\le {\sin }^{-1}\left(\frac{\lambda }{2L}\right)\le \frac{\pi }{2}$가 되므로 각도 모호성이 발생하지 않게 된다.

그러나 안테나 소자의 물리적 크기, 이득, 빔폭, 격리도 등의 설계 제한 요소를 고려할 때 안테나 간격을 반파장 이하로 설계하는 것은 사실상 불가능에 가까우므로, 일반적으로 간섭계 안테나를 다중 기준선으로 설계하여 각도 모호성 발생을 해소한다^[8].

단일 기준선 간섭계의 각도 모호성을 해소하기 위해 2쌍 이상의 다중 기준선 간섭계를 구성하여 위상비교 모노펄스 알고리즘으로 위상을 추정하고, 이들 위상을 비교하여 표적 각도를 추정한다^[12],[13]. 이를 위해 3개 이상의 안테나를 구성하는데, 본 논문에서는 3개의 안테나로 각도 모호성을 해소한다.

그림 2와 같이 다중 기준선에 배치된 3개의 안테나 Ant1, Ant0, Ant2로 식 (1)의 표적반사신호 S_r이 수신된다고 하면 각 안테나에서의 수신신호 위상은 각각 ϕ₁, ϕ₀, ϕ₂가 된다. 수신신호의 각 안테나 채널 간에 측정한 상대 위상차를 Δϕ₁, Δϕ₂라고 할 때 이들은 식 (2)와 동일한 방법으로 식 (6)과 같이 구할 수 있다.

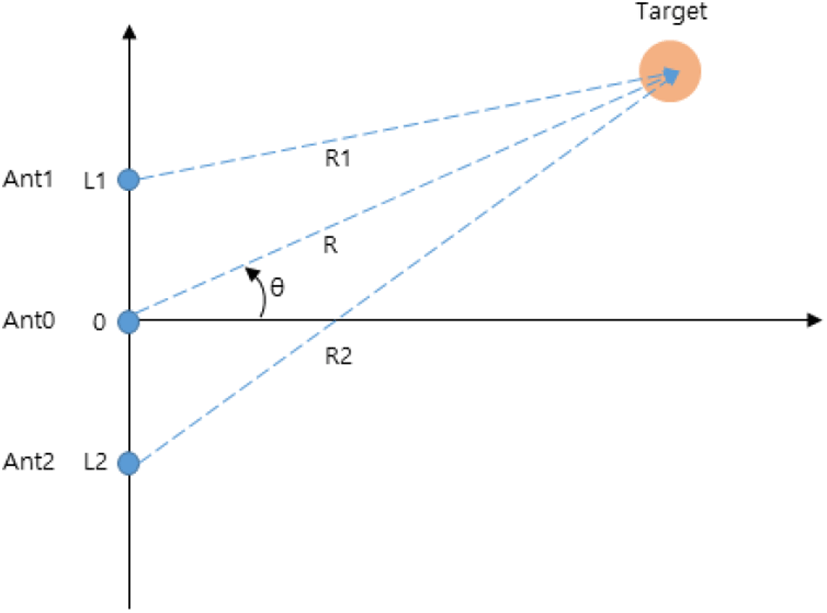
한편, 추정 위상차 Δψ₁, Δψ₂는 그림 2의 기하구조로부터 구할 수 있다. 중심 안테나 Ant0과 L₁만큼 이격되어 있는 Ant1과의 경로차 R₁-R은 R이 매우 클 때 테일러 전개 및 포물선 근사에 의해 식 (7)로부터 식 (8)과 같이 간략화할 수 있다^[14]. 이 때 Δψ₁은 식 (3)에 의해 식 (9)와 같이 구할 수 있다.

동일한 방법으로 중심 안테나 Ant0과 L₂만큼 이격되어 있는 Ant2와의 추정 위상차 Δψ₂는 식 (10)과 같이 구할 수 있다.

단일 기준선 간섭계와 동일한 이유로 측정 위상차 Δϕ₁, Δϕ₂와 추정 위상차 Δψ₁, Δψ₂는 식 (11)과 같은 관계를 갖는다. 이 때 n과 m은 주기성을 나타내기 위한 정수값이다.

이 값을 식 (9), 식 (10)에 대입하면 식 (12), 식 (13)을 얻을 수 있다.

위 식과 관련하여, 다중 기준선 간섭계에서는 간격 L₁, L₂를 다르게 함으로써 sin(θ₁)과 sin(θ₂)가 다른 기울기와 다른 절편을 갖도록 설계하고, 두 값의 차이가 최소가 되는 값이 참값일 것이라는 가정하에 식 (14)를 만족하는 변수 n, m을 구한다.

위 식에서 각도 θ는 안테나의 반전력 빔폭 2θ_width 이내 값이다. sin(θ₁)과 sin(θ₂)의 차이가 최소가 될 때의 변수 n, m을 구하여 식 (12), 식 (13)에 대입함으로써 sin(θ₁)과 sin(θ₂)를 구하고, 이 값을 산술평균하여 식 (15)와 같이 표적 각도 $\widehat{\text{θ}}$를 추정한다.

간섭계 안테나를 슬롯 배열로 설계하고^[15], 이득, 빔폭, 격리도 등을 고려하여 기존의 다른 방법들처럼^[9],[10] SNR과 L₁, L₂를 기반으로 각도 측정 오차와 각도 모호성을 분석하여 그림 3의 형태로 L₁, L₂를 설계 및 제작하였다.

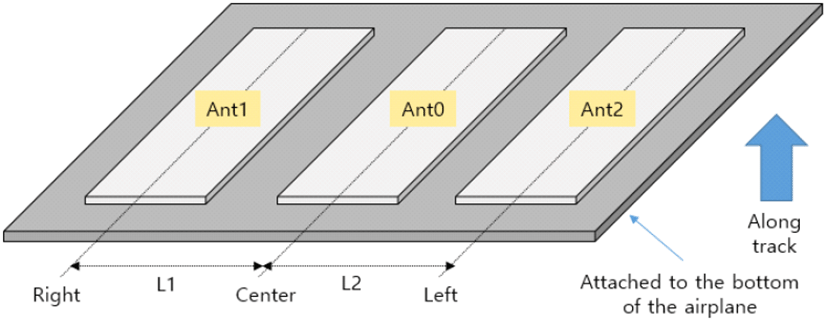
이 때 안테나의 3 dB 빔폭은 방위각 30°, 고각 10° 수준이며, 안테나 방향은 비행방향과 비행기 하부에 부착되는 점을 고려하여 Ant1을 오른쪽 안테나, Ant2를 왼쪽 안테나로 규정하였다. 이를 이용하여 비행탑재시험을 수행하였고, 분석 결과 중 한 컷을 그림 4에 나타내었다.

위 그림 4(a)는 현재 GPS 위치에서의 DEM 고도를 비행 진행(along track) 방향의 직각(cross range) 방향에 대해 나타낸 것으로 간섭계 레이다 고도계의 관측 가능 영역 (1)을 붉은색으로 표시하였다. 이 때 최근점 Target 1의 고도 H_d는 350 m 수준이며, 각도(방위각)는 0° 수준으로 판단된다.

그림 4(b)는 간섭계 레이다 고도계에서 관측한 이격거리(식 (7)의 R)별 수신 전력을 나타낸 것으로 그림 4(a)의 붉은색 영역에 대응하는 거리를 붉은색으로 표시하였다. 이 때 Threshold 이상의 신호를 표적군으로 추정하는데, 간섭계 레이다 고도계와 최근점 Target1 사이의 이격거리 R과 GPS 상의 고도 H_g는 H_d=H_g-R 의 관계를 만족한다.

그림 4(c)는 식 (15)에서 추정한 이격거리별 각도(푸른색)와 관측 가능 영역 (1)에서의 실제 DEM 각도(붉은색)를 함께 나타낸 것이다. 만약 추정 각도가 정확하다면 붉은색 점선과 푸른색 점선은 유사할 것이고, 추정 각도에 오차가 있더라도 일반적으로는^[9],[10] 붉은색 점선 근방에 푸른색 점선이 있을 것으로 예상할 수 있다.

그러나 영역 (1)에서 최근점 주변의 DEM 각도는 0° 부근이지만, 영역 (2)에서 식 (15)는 0°가 아니라 −10°, 10°, 20° 등 다양한 각도를 추정하고 있음을 알 수 있다. 그래도 영역 (3)에서는 붉은색 점선과 푸른색 점선이 유사하나, 영역 (4)에서는 다시 일정 간격으로 도약하면서 발생하는 각도 오차(푸른색 점선)가 존재함을 확인할 수 있다.

이는 점 표적이 아닌 연속적인 지형을 관측하는 간섭계 레이다 고도계 특성 상, 유사 거리에 있는 지형끼리는 위상 중첩이 발생하여 점 표적 대비 큰 위상 오차가 발생할 수 있을 것으로 판단된다. 그리고 도약에 의한 각도 오차가 일정 간격으로 빈번하게 발생하는 것을 미루어 볼 때 기존^[9],[10]과 다른 형태로 다중 기준선 간섭계에 각도 모호성이 발생하고 있는 것으로 예측할 수 있다.

본 장에서는 2-3절에서 예측된 간섭계 레이다 고도계의 특유의 각도 모호성을 다음과 같은 방법으로 분석한다. 먼저 식 (12), 식 (13)을 식 (16), 식 (17)과 같이 변환한다. 이 때 R≫L₁이므로 $\frac{L_1}{2R}$은 생략한다. $\frac{L_2}{2R}$도 마찬가지이다.

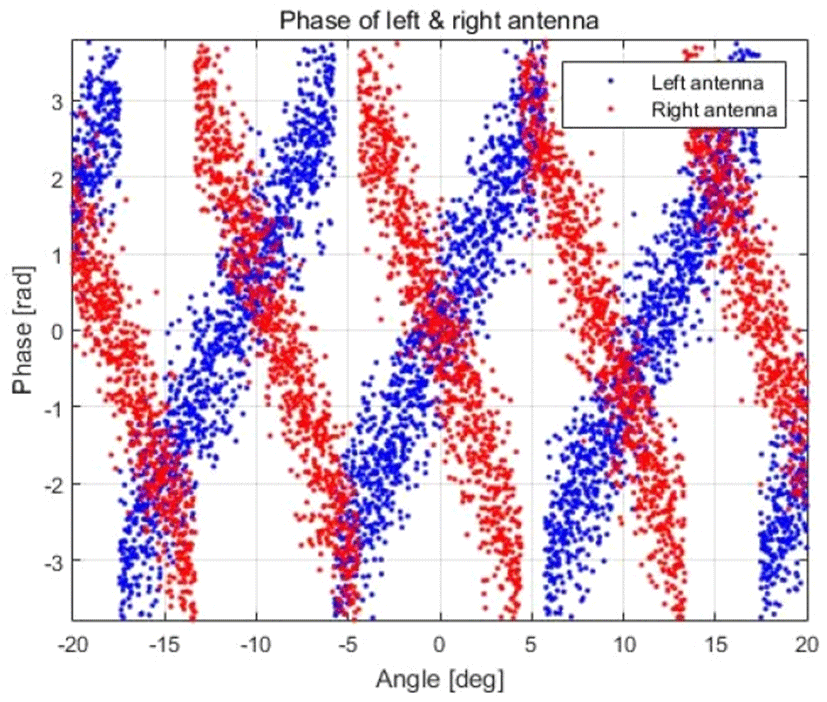
식 (16), 식 (17)에서 L₁, L₂를 설정하고, n과 m에 음수부터 양수까지 여러 정수 값을 대입하면 그림 5와 같이 관심 각도 영역에서의 각도 대 위상 그래프를 구할 수 있다. 이 때 L₁은 오른쪽 안테나 중심점(좌표상 양수), L₂는 왼쪽 안테나 중심점(좌표상 음수)으로 규정한다.

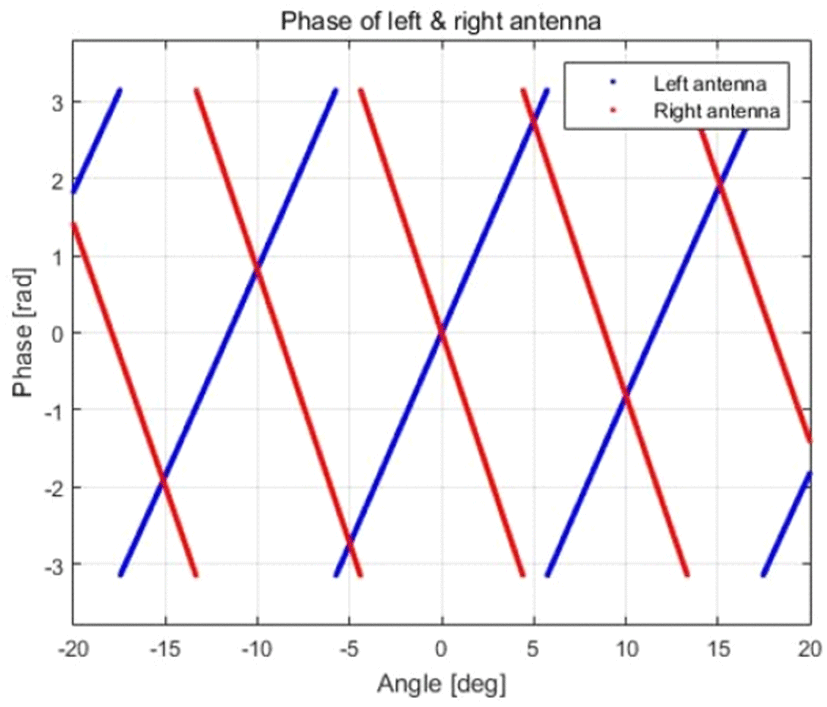
이를 기반으로 다중 기준선 간섭계에 대한 위상비교 모노펄스 알고리즘을 적용하면 그림 6과 같이 입력 각도(참값)에 대한 출력 각도(추정 값) 그래프를 구할 수 있다.

따라서 이론적으로는 위상비교 모노펄스 알고리즘이 입력 각도를 잘 추정하고 있음을 확인할 수 있다. 그러나 2-3절에서, 실제 추정 결과는 ‘참값 ± 오차’가 아니라, 오차가 수시로 도약하면서 변했기 때문에 도약 오차가 다중 기준선 설계와 관련이 있는지를 분석할 필요가 있다.

각도 모호성 현상 분석을 위해 식 (16), 식 (17)을 아래 식 (18), 식 (19)와 같이 변환한다. 이 때 입력 각도 X₁은 모수가 θ₁과 σ²인 정규분포를 따른다. X₂도 θ₂에 대해 마찬가지이다. 그리고 가능한 많은 도약 각도 오차를 관찰하기 위해, 시스템 설계 오차 σ_s의 2배 수준의 위상 오차 σ₀를 σ에 대입하고, X₁ 및 X₂에 대해 몬테카를로 시뮬레이션을 수행하여 그림 7과 그림 8의 그래프를 구하였다.

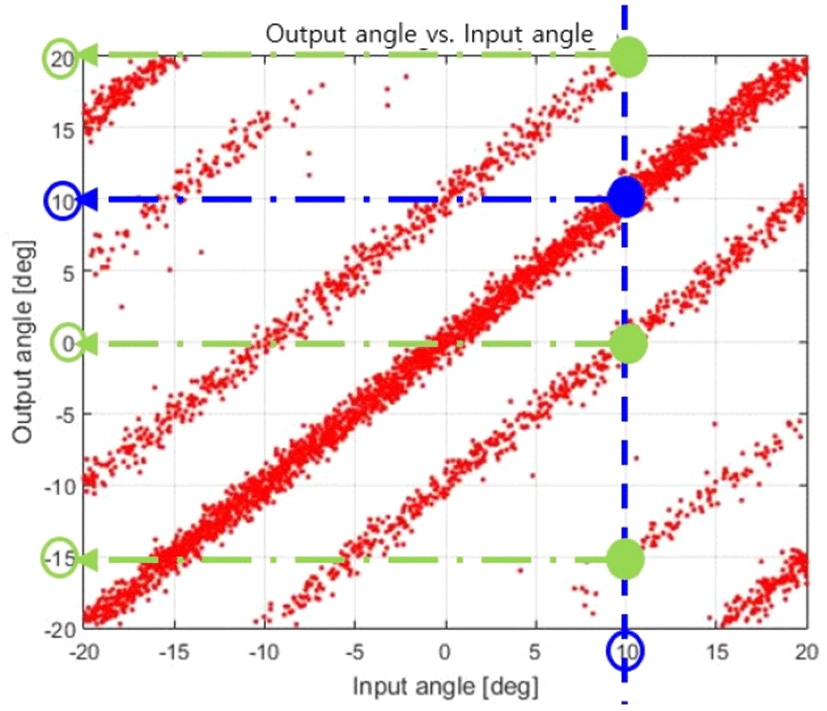
그림에서, 입력 각도가 10°라면 빈도의 차이는 있지만 참값(푸른색) 10°가 가장 빈번하게 발생하고, 20°(10°+ 10°), 0°(10°−10°) 부근의 각도 모호성(초록색) 또한 빈번하게 발생할 수 있고, −15° 부근의 각도 모호성(초록색)도 가끔 발생할 수 있음을 알 수 있다.

그리고 그림 4(c) 영역 (3)에서 참값 6°에 대한 추정각도가 큰 폭으로 도약하는 현상으로부터, 실제 시험에서 발생하는 각도 모호성 현상을 본 논문의 각도 모호성 분석 결과가 잘 설명할 수 있음을 확인할 수 있다.

다중 기준선에 내재하는 각도 모호성이 간섭계 레이다 고도계의 주요 각도 오차 중 하나임을 확인하였다. 그런데 이 각도 오차는 일반적인 오차처럼 무작위로 발생하는 게 아니라, 그림 8처럼 뚜렷한 경향성을 가지고 발생하기 때문에 신호처리로는 참값과의 구분이 쉽지 않다.

따라서 본 논문에서는 신호처리 전 단계에서 이러한 각도 모호성을 최소화하기 위해 식 (18), 식 (19)를 기반으로 여러 L₁, L₂에 대해 몬테카를로 시뮬레이션을 수행하여 각도 모호성(표 1)과 각도 측정 오차(표 2)를 분석하고, 최적의 설계 파라미터 L₁, L₂를 도출하였다.

이 때 위상 오차는 시스템 설계 오차 σ_s를 분석하여 대입하였고, 설계 제한 요소를 고려하여 제작 가능한 L₁, L₂ 값을 후보군으로 선정하였다. 참고로 표 1의 각도 모호성은 입력값 대비 출력값이 허용오차(예: ±5°)를 초과하는 도약 오차 값의 빈도를 계산한 결과이고, 표 2의 각도 측정 오차는 도약 오차 값은 배제하고, 참값 주변 값으로만 참값과의 측정 오차를 계산한 결과이다.

표 1에서 각도 모호성이 다른 L₁, L₂ 후보군 3쌍을 선정하였다. 이 중 6 λ / −4.5 λ과 6.5 λ / −5 λ는 각도 모호성이 작은 쌍으로서 선정 후보군이고, 7 λ / −4.5 λ는 각도 모호성이 약간 높은 쌍으로서 비교 후보군이다. 그리고 이 후보군들의 각도 측정 오차를 표 2에 나타내었다. 그 결과, 각도 측정 오차는 대부분 0.3° 수준으로 큰 차이가 없었다. 이에 이 후보군들의 입력 각도 대 출력 각도 그래프를 그림 9와 같이 분석하였다.

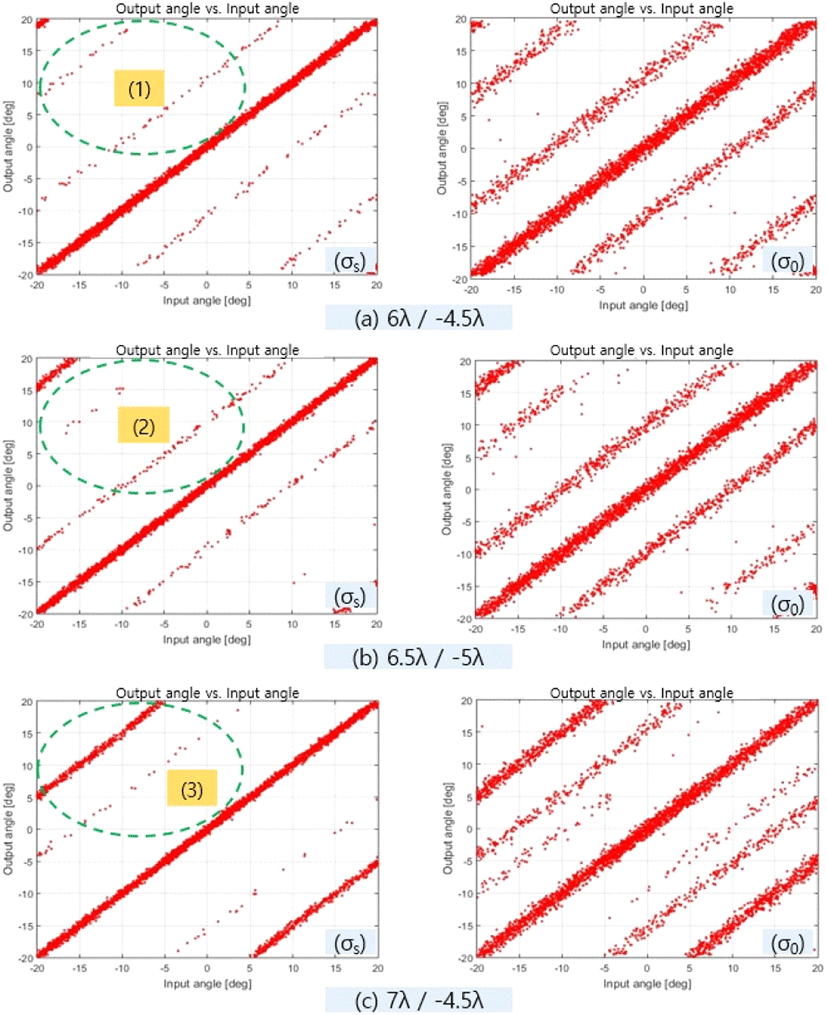
그림 9에서 좌측 열은 시스템 설계 오차 σ_s에 대해 분석한 결과로서 기준선 설계를 위해 나타내었으며, 우측 열은 그림 8에서 대입했던 오차 σ₀를 동일하게 대입한 결과로서 결과 비교를 위해 나타내었다.

그림 9(a)~그림 9(c)의 좌측 열에 대해 영역 (1)~(3)을 관찰해 보면, 영역 (1)에서는 영역 (2)의 도약 오차군보다는 빈도가 낮은 2쌍(± 12°, ± 28° 수준)의 도약 오차군이 −15°~15° 구간에서 발생한다. 영역 (2)에서는 참값보다는 빈도가 낮은 1쌍(± 10° 수준)의 도약 오차군이 −15°~15° 구간에서 발생하나, 15°~20°와 −20°~−15° 구간에서는 참값과 유사한 빈도의 치명적인 도약 오차군이 발생한다. 영역 (3)에서는 3개 영역 중 빈도가 가장 낮은 1쌍(± 15° 수준)의 도약 오차군이 −5°~5° 구간에서 발생하나, 5°~20°와 −20°~−5° 구간에서는 참값과 유사한 빈도의 치명적인 도약 오차군이 발생한다.

이 결과로부터 안테나의 반전력 빔폭이 30°(= ± 15°) 이내라면 L₁, L₂를 6 λ/−4.5 λ나 6.5 λ −5 λ로 설정하는 것이 합리적인 것으로 판단되나, 그림 9의 우측 열처럼 위상 오차 σ₀가 클 경우에는 각도 모호성이 빈번하게 발생할 수 있음을 예상할 수 있다. 이에 본 논문에서는 안테나의 설계 제한 요소 중 격리도 조건을 완화하여 L₁, L₂를 3.5 λ /−5 λ로 설정하고, 시뮬레이션을 수행하여 결과를 그림 10에 나타내었다.

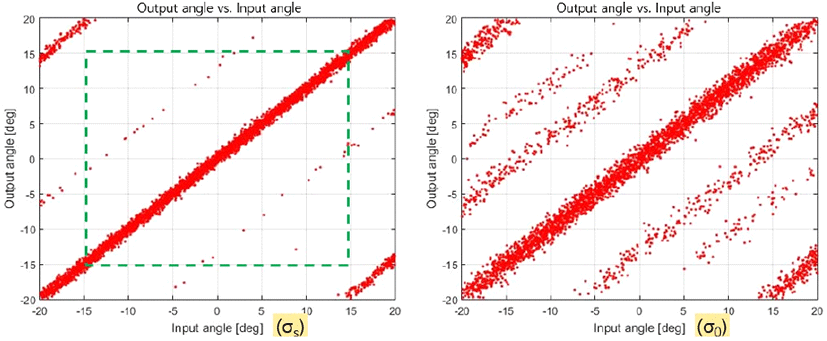
그림 10에서 좌측 열은 시스템 설계 오차 σ_s, 우측 열은 오차 σ₀를 대입한 결과이다. 좌측 열에서 각도 모호성은 8.49 %로, 각도 측정 오차는 0.38°로 추정되었다. 다만 이 경우 L₁과 중심과의 거리가 너무 가깝기 때문에 안테나 이득 및 빔폭 등에 따라 안테나 간 격리도가 떨어져 표적 탐지 성능이 저하될 수도 있다. 참고로 안테나 수신 영역을 영역 (1) −15°~15°으로 한정하면 각도 모호성은 3.92 % 수준으로 감소한다. 우측 열은 그림 8과의 비교를 위해 나타내었다. 우측 열에서 그림 8보다는 도약 오차 빈도가 낮음을 알 수 있으나, 큰 위상 오차 σ₀에 대해서는 각도 모호성이 빈번하게 발생할 수 있음을 예상할 수 있다.

비록 다양한 설계 조건에 대한 분석 결과는 아니지만, 본 논문에서 제시하는 바와 같이 주어진 설계 제한 조건 내에서 파라미터를 설정하고 각도 모호성을 분석하면, 신호처리 전 단계에서 도약 각도 오차에 의한 각도 모호성을 최소화할 수 있는 안테나 기준선을 설계할 수 있을 것으로 판단된다.