Ⅰ. 서 론
위상배열 안테나 기반의 능동형 전자주사식 위상배열 (active electronically scanned array: AESA) 레이다는 공대지 탐지 모드 운영 시 항공기 안테나의 boresight 방향을 따라 명확하지 않은 지표면까지의 거리를 추정하는 공대지 거리측정이 요구된다[1]. 이를 위해 항공기 기동, 안테나 빔 조향, 지표면 클러터 환경과 같이 다양한 운영 제원을 고려하여 생성된 지표면 반향 합(sum) 및 고각 차(difference) 패턴 신호의 모노펄스 비로 boresight 방향 거리를 추정한다[2]. 하지만 지표면 클러터 환경은 지표면 반향 신호에 큰 영향을 미치므로[3] 이에 따른 분석과 항공기 회전 기동 시 빔 패턴 왜곡으로 거리 추정 오차가 발생하므로 이에 대한 보상이 필요하다[4]. 또한, 클러터 신호의 랜덤 특성이 모노펄스 신호들에 영향을 줘, 거리 추정에 오차가 발생할 수 있어 오차 감소를 위한 프로세싱이 요구된다.
본 논문에서는 다양한 운영 제원을 고려하기 위해 항공기 안테나 송신 주파수, 지표면 클러터의 시간과 주파수에 따른 변화 등을 고려한 레이다 반사 신호를 생성한다. 거리 추정을 위해 생성된 신호를 두 가지 방법으로 결합하고, 이를 처리하여 거리를 예측한다. 이때 항공기 회전 기동에 따른 빔 패턴 왜곡을 레이다의 모노펄스 축과 지표면에 투영된 모노펄스 축 간의 차이를 이용하여 보상한다. 이런 신호 생성방법과 보상방법은 II절에서 기술하고, III절에서는 수치적으로 정확하고 효율적인 거리 추정 알고리듬을 제안한다. IV절에서는 다양한 운영 제원을 고려한 시나리오에 대한 제안한 방법의 성능 시뮬레이션을 제시한다.
Ⅱ. 지표면 수신신호 모델링
다양한 클러터 환경 및 항공기 기동에 따른 레이다 신호 모사는 참고문헌 [2]에 기술되어 있고, 간단히 다음과 같이 요약할 수 있다. 그림 1에서 보듯이 일정한 속도로 비행하는 항공기 레이다가 지표면을 향할 때 지표면 투영영역은 주엽(mainbeam)의 반전력빔폭(half power beam width: HPBW)으로 근사한다[5]. 투영영역은 line of sight (LoS)에 평행한 장축과 이에 수직한 단축에 각각 평행하도록 원거리 장을 가정하여 사각형으로 차분화한다. 차분화 된 각 영역마다 지표면 클러터 산란특성을 나타내기 위해 후방산란계수(σ0)[6]를 분산으로 사용하여 랜덤 수신 신호를 생성한다. 신호 송신 시 합 패턴 배열 가중치(array weight)를 이용하고, 수신 시 합 외 두 개의 차 패턴 배열 가중치를 이용하여 세 개의 모노펄스 수신 신호를 생성한다[1].
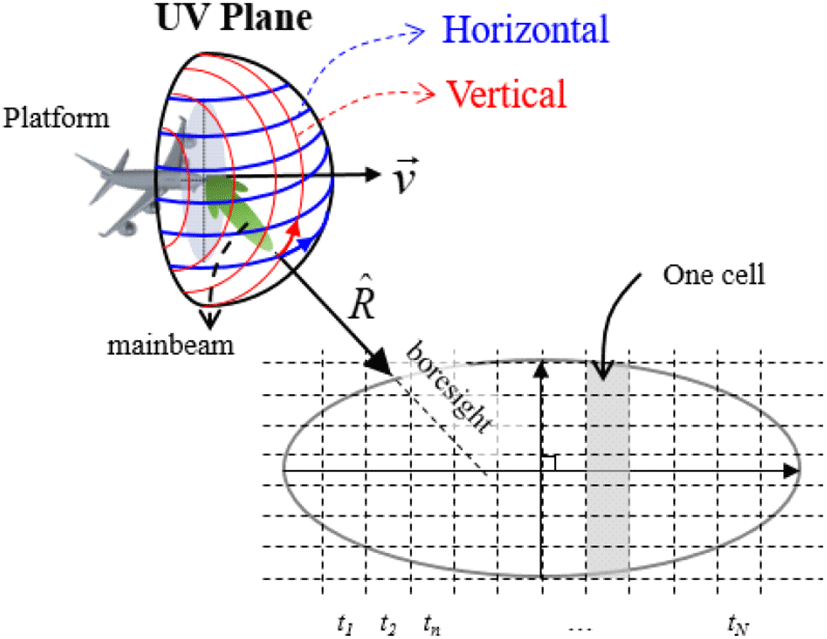
실제 항공기는 이동과 동시에 신호(pulse)의 송수신을 펄스반복주기(pulse repetition interval: PRI) 기반으로 반복한다. 각 PRI 동안의 시간 흐름은 fast-time(t)이며, 펄스를 송신하는 시점들의 집합은 slow-time(η)이다[2]. 그러므로 수신 신호는 두 시간에 대한 2D 신호가 되며, 공대지 거리측정을 위해 Coherent integration processing과 Non-coherent integration processing 방법으로 신호를 결합한다.
Coherent integration processing 방법은 신호 송신 시 펄스마다 동일 송신 주파수(f)를 이용한다. 각 펄스의 지표면 반사 신호는 서로 상관관계가 있어 이를 상관시간(correlation time, tc)을 이용하여 모델링하고, 최종적으로 2D신호를 생성한다[2],[7]. Non-coherent integration processing 방법은 신호 송신 시 펄스마다 Δf씩 주파수 도약(frequency hopping)을 한다. 지표면 반사 신호는 상관주파수(correlation frequency, fc)를 가정하여 앞서와 같이 상관된 2D 신호를 생성할 수 있다. 반사도가 큰 물체(man-made target)의 신호 생성을 위해 임의의 차분화 된 영역 내에 반사도가 큰 물질을 가정하고, 이의 반사도 크기를 target-to-clutter ratio(TCR)로 정의한다. 차분화 된 영역에서 반사되는 2D 레이다 신호를 생성한 후 항공기 속도에 따른 도플러 효과를 부여한다[2].
앞서 언급한 두 가지 프로세싱으로 생성된 상관된 2D 신호들은 항공기 회전 기동 시 투영영역 왜곡으로 인하여 거리 추정 오차가 발생하므로 이에 대한 보상이 필요하다[4]. 그림 1에서 고각(θ)과 방위각(φ)은 각각 UV plane의 수직과 수평축을 기준으로 변한다. UV plane 상의 모노펄스 수직축과 수평축을 빔 조향 방향 벡터로 각각 지표면에 투영할 경우, 그림 2와 같이 모노펄스 수직축과 수평축을 형성한다.
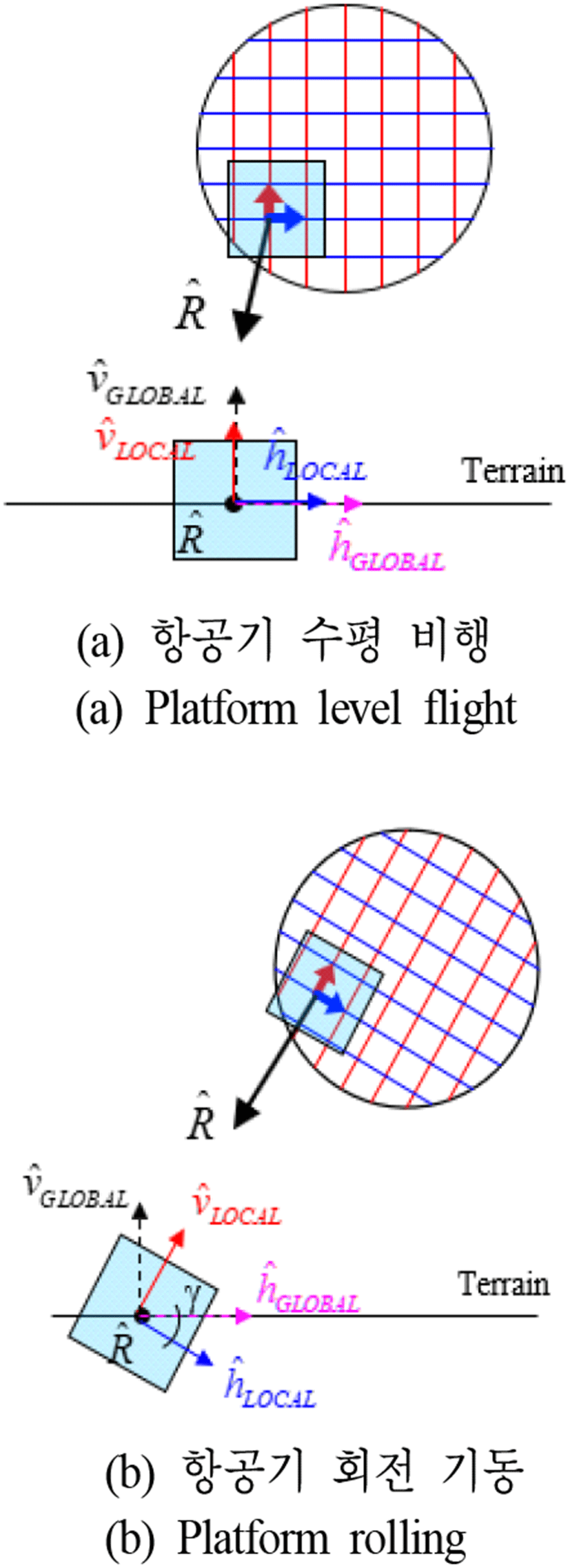
그림 1의 항공기 안테나 UV plane을 위에서 본 경우, 그림 2와 같고, 그림 2(a)는 수평 비행, 그림 2(b)는 회전 기동 시의 UV plane과 지표면에 투영된 모노펄스 수직축과 수평축을 보여준다. 그림 2(a)와 같이 항공기 수평 비행 시 모노펄스 수평축과 지표면 수평축은 일치하므로 빔 패턴에 왜곡이 발생하지 않지만, 그림 2(b)와 같이 항공기 회전 기동 시 수평축 간에 γ만큼 차이가 발생하며, 이에 따라 빔 패턴 왜곡이 발생한다. 따라서 식 (1)을 이용해 γ계산하고[1], 식 (2)의 회전 행렬에 γ를 적용하여 보정 전 고각과 방위각 차 패턴 신호를 보상한다. θp과 θr은 각각 항공기 기동 pitching과 rolling 각도를 나타내며, 여기서 /woγ는 gamma correction이 없는 경우이다.
γ 보정 후 고각 및 방위각 차 패턴 신호들은 coherent와 non-coherent integration processing으로 신호를 결합한 후 모노펄스 비를 통해 항공기로부터 지표면까지 거리를 추정한다. 여기서 /wγ는 gamma correction이 있는 경우를 나타낸다.
Ⅲ. 공대지 거리측정 알고리듬
Coherent integration processing에서 상관된 2D 신호를 slow-time 축으로 고속 푸리에 변환(fast Fourier transform: FFT)를 적용하여 Range-Doppler map(RD-map)을 계산하고, 합과 고각 차 RD-map의 비로 모노펄스 비를 생성한다[2]. 하지만 RD-map 전체를 계산할 경우 데이터 처리 시간 및 추정 오차가 증가할 수 있어, 거리 추정에 필요한 영역을 설정한다. RD-map에서 주파수 축 영역(Δfreq)은 항공기 속도에 따른 RD-map의 중심 도플러 주파수를 기준으로 설정한다. 거리 축 범위(Δrange)는 항공기와 안테나의 기동에 따라 지표면 투영영역까지 추정된 거리를 기준으로 설정한다. 설정된 영역의 모노펄스 비를 계산하고, 도플러 축으로 평균과 크기를 취하면 하나의 모노펄스 비가 계산된다. 이를 임의 차수의 다항식으로 근사화(fitting)한 후 다항식의 최솟값을 찾아 공대지 거리를 예측한다. Non-coherent integration processing 방법은 생성된 2D 신호에서 추정된 거리의 일정한 범위(Δrange)내 신호들의 비를 구한다. 이때 각 신호들의 주파수가 다르므로 크기만 고려하여 비를 구하고, 이의 평균을 계산하여 최종 모노펄스 비를 구한다. 앞서 설명한 방법과 같이 다항식을 이용하여 거리 추정을 한다. 제안하는 다항식 기반 거리 추정 방법의 정확도에 영향을 주는 요소로 다항식의 차수, 거리 및 주파수 범위, fitting에 사용하는 데이터 수 등이 있다. 예를 들어 다항식 차수에 따른 거리 추정 오차를 그림 3이 보여준다.
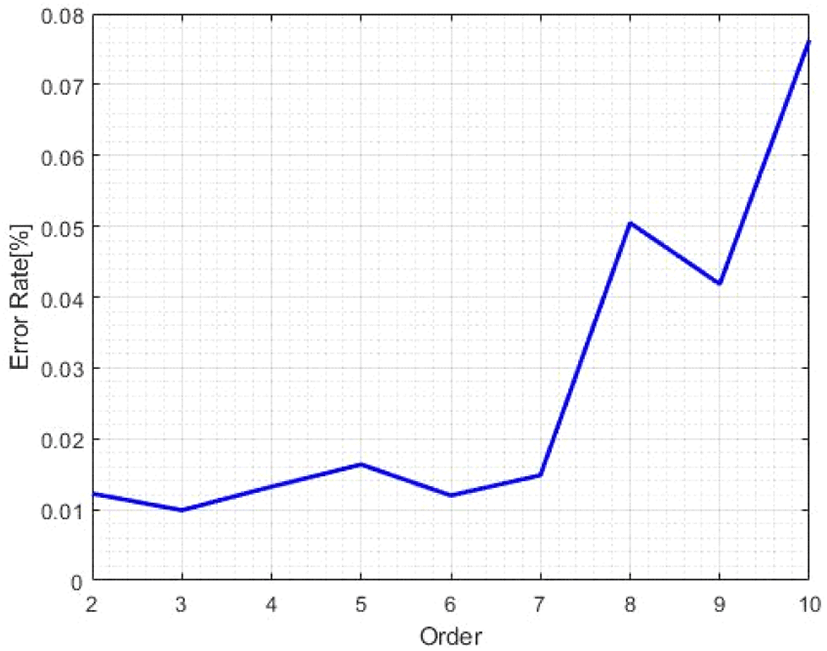
시뮬레이션 환경은 coherent integration processing으로 항공기 도플러 효과를 고려하며, 지표면은 동일한 클러터 환경으로 가정하였고, 지표면 클러터 시간에 따른 변화(tc)는 3 ms를 가정하였다. 항공기 기동은 pitch(θp)=0°, roll(θr)=0°이고, 안테나 빔 조향은 elevation(θ)=110°, Azimuth(φ)=0°이다. 100회 몬테카를로 시뮬레이션 결과, 낮은 차수의 다항식을 사용해도 정확도가 유지됨을 알 수 있어, 본 논문에서는 2차 다항식을 사용하였다. 다른 요소들은 여러 시뮬레이션을 통해 결정되었다: Δfreq, Δrange는 각각 20 %, 7 % 이상에서 오차율이 안정됨을 확인하였고, 데이터 수는 거리 추정에 큰 영향이 없으나, 15개 이상으로 설정한다. 또한 데이터 간의 랜덤한 특성을 최소화하기 위해 윈도우 길이(lw)와 표준편차(σ)가 1인 햄펄(hampel) 필터로 데이터의 이상 값을 제거한다.[8]
Ⅳ. 시뮬레이션 결과
표 1은 두 가지 프로세싱 시뮬레이션에 대한 지표면 반사 신호 파라미터를 보여준다. 항공기 안테나로부터 여러 번의 펄스를 송수신한 신호들의 합 신호 RD-map은 그림 4(a), 4(b)와 같으며, Non-coherent integration processing으로 slow-time을 따라 신호를 결합하면 그림 4(c), (d)와 같다. 그림 4의 경우, 항공기와 지표면 클러터 도플러 효과를 고려하고, 지표면은 동일 클러터로 가정하였다. 항공기 기동과 안테나 빔 조향은 θp=0°, θr=45°, θ=110°, φ=0°이다. 그림 4(a), 4(b)에서 항공기 속도에 따른 도플러 주파수는 11,276.3 Hz이며, tc가 길수록 RD-map의 도플러 주파수 범위가 좁아진다[2]. 또한, fc가 클수록 slow-time으로 신호들의 상관관계가 커지므로 신호를 결합할 경우에 랜덤할 수 있다.
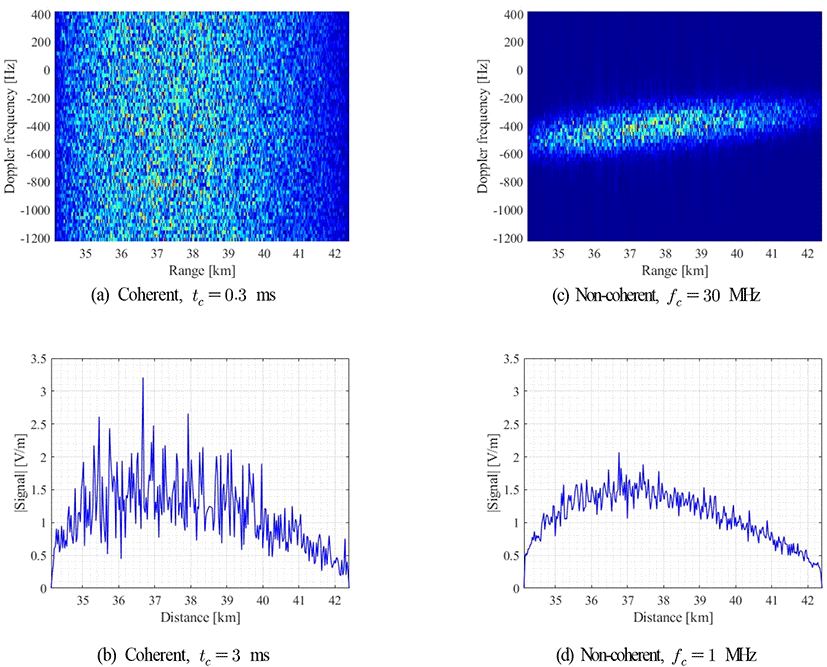
항공기 레이다가 지표면을 향할 때 지표면에 투영된 영역 내에는 다양한 클러터 환경이 존재할 수 있다. 그림 5의 항공기 기동과 빔 조향은 θp=0°, θr=45°, θ=110°, φ=0°이며, 신호 결합 방법에 따른 이종클러터와 반사도가 큰 물체를 고려한 합 신호 RD-map과 신호를 보여준다.
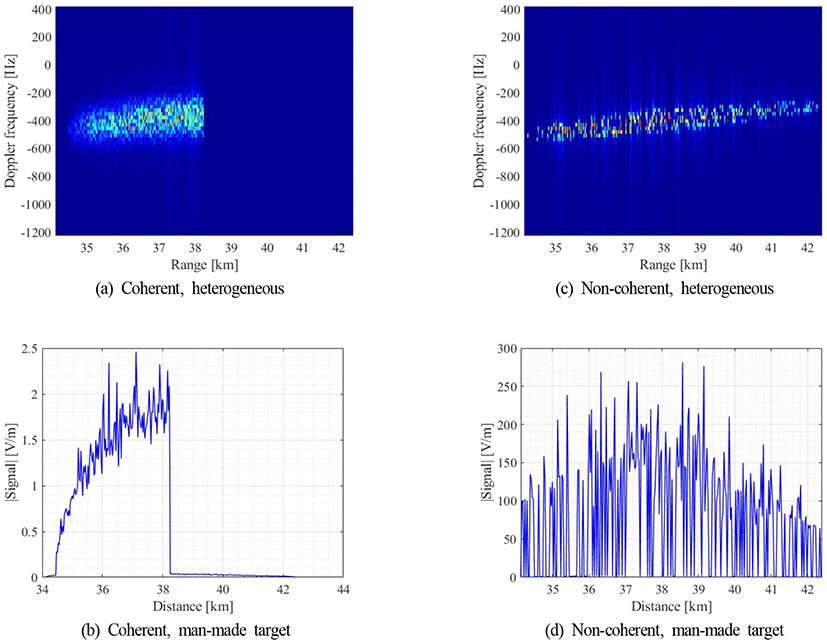
그림 5(a), 5(c)는 두 종류의 클러터가 존재하는 경우의 신호를 보여주고, 그림 5(b), 5(d)는 반사도가 큰 물체가 존재하는 경우 신호를 보여준다. 그림 5(a), 5(c)의 클러터 특징은 각각 tc=3 ms, fc=1 MHz이며, range≤38.2 km에서 투영영역의 평균 제곱근(root mean square: RMS) 높이(h)는 0.8 cm, 이외 영역은 0.01 cm로 가정하여 이종클러터를 생성하였다. 모노펄스 레이다로 지표면으로부터 수신되는 신호는 후방산란계수의 평균 제곱근 높이에 비례하므로[6], 그림 5(a), 5(c)는 다른 클러터에서 반사되는 레이다 수신 신호의 크기 차이를 명확하게 보여준다. 그림 5(b), 5(d)는 투영영역 내 TCR=13 dB인 물체 300개를 랜덤하게 배치시켰으며, 배치된 영역에서 레이다 반향 신호가 크게 발생하는 것을 확인할 수 있다. 또한, 항공기 도플러 효과를 반사도가 큰 물체 이후에 고려하므로 그림 5(b)의 RD-map에서 도플러 주파수 범위 내에 물체가 위치함을 알 수 있다. 이종클러터와 반사도가 큰 물체를 고려하면서 항공기 회전 기동에 따른 보정이 필요하다.
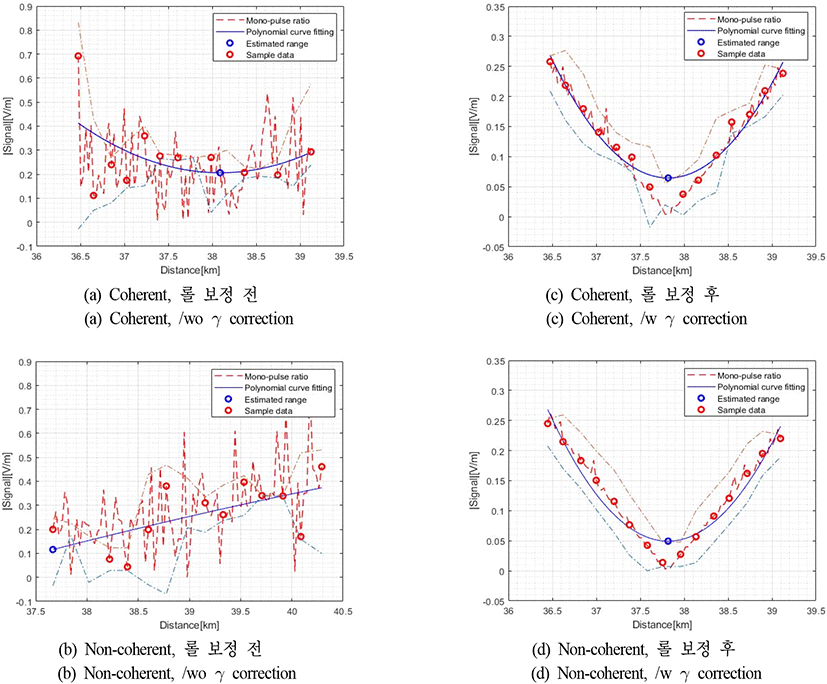
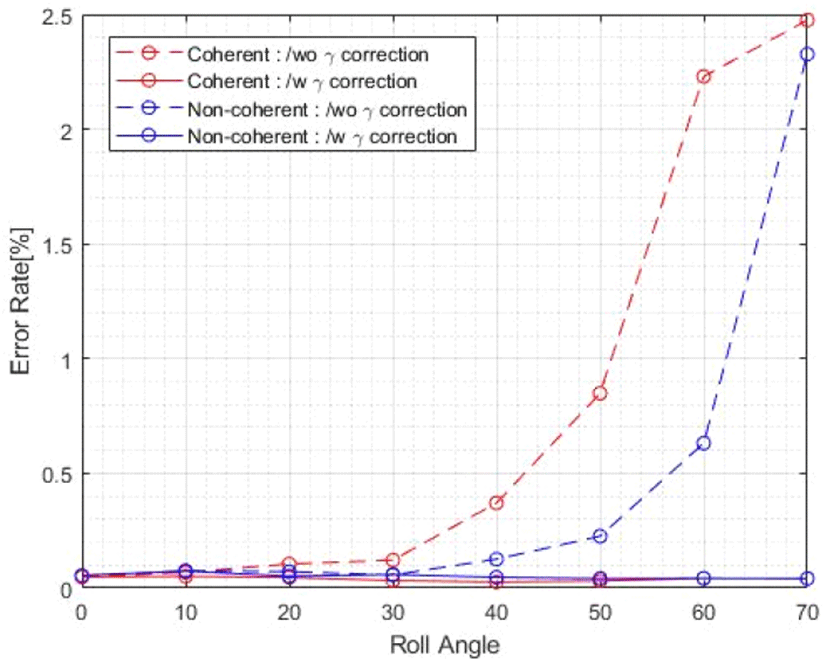
그림 6은 그림 5에서 제안된 이종클러터와 반사도가 큰 물체를 고려하며, lw=1, σ=1의 햄펄 필터를 적용한 15개의 데이터를 2차 다항식 곡선 접합한 γ 보정 전후 모노펄스 비를 보여준다. 항공기 기동과 빔 조향은 θp=0°, θr=45°, θ=110°, φ=0°이다. γ 보정 전에는 모노펄스 수평축이 지표면 수평축과 일치하지 않아, 차 신호가 크게 왜곡되어 모노펄스 비가 왜곡됨을 그림 6(a), 6(c)에서 확인할 수 있다. 이때 비의 최솟값을 찾을 수 없어 거리 추정에 오차가 생긴다. 그림 6(b), 6(d)는 γ 보정 후 모노펄스 비를 보여준다. 이 경우, 왜곡이 없어 최솟값을 효율적으로 찾을 수 있으므로 정확한 거리 추정이 가능하다. 실제 거리는 37,809 m이며, 추정된 거리는 각각 37,817 m, 37,859 m로 수치적으로 작은 오차를 보인다. 그림 6에서 일점쇄선은 햄펄 필터를 통한 이상 값 검출 범위를 나타내며, 실선과 점선은 2차 다항식과 실제 레이다 신호 결과이다. 모노펄스 시스템은 합 패턴 신호 송수신 후 3개의 신호를 생성하므로 지표면 클러터에 의한 랜덤 특성이 3개의 신호에서 동일하게 영향을 줘, 그림 6(b), 6(d)에서 보듯이 모노펄스 비는 크게 영향을 받지 않는다. 항공기 회전 각도에 따른 γ 보정 전/후 정확한 수치적 비교를 위해 그림 7은 회전 각도마다 100회의 몬테카를로 시뮬레이션 결과를 보여준다. 항공기 기동과 빔 조향은 θp=0°, θr=0°~70°, θ=110°, φ=0°이며, Δfreq, Δrange 는 각각 20 %, 7 %, 15개의 데이터와 2차 다항식 곡선 접합으로 수행하였다. Coherent와 non-coherent integration processing은 γ 보정 전에는 롤 각도가 증가함에 따라 거리 추정 오차율이 증가하지만, γ 보정 후 매우 적은 오차율을 보인다. 최대 오차율은 coherent 및 non-coherent인 경우, 각각 0.073 %, 0.051 %이며, 수치적으로 매우 적음을 알 수 있다.
Ⅴ. 결 론
본 논문에서는 지표면 클러터 환경을 고려한 모노펄스 레이다의 지표면 반사 신호 생성과 항공기 회전 기동에 따른 왜곡 보상 후 모노펄스 비에서 거리 추정 오차를 최소화하는 방법을 제안하였다. 실 운영과 같이 합 패턴 신호를 송수신하고, 세 가지 패턴 신호를 안테나 배열 가중치를 이용하여 합성하여, AESA 안테나의 빔 왜곡 특성 등을 정확하게 고려할 수 있다. 지표면 투영영역 내 다른 거칠기의 지표면과 일정한 영역에 반사도가 큰 물체가 존재하는 경우의 레이다 반사 신호를 생성하며, 이런 다양한 경우에 적용 가능한 공대지 거리측정 방법을 제안하였다. Coherent 또는 non-coherent 방법에 따른 반사 신호를 생성하고, 이의 일부분을 이용하여 모노펄스 비를 계산한다. 지표면 반향 신호의 랜덤 특성을 최소화하기 위해 햄펄 필터를 이용하며, 모노펄스 비를 2차 이상 다항식 곡선 접합한 후 최솟값을 찾는다. 제안된 방법에 영향을 미치는 인자들을 다양한 경우에 대해 시뮬레이션한 후 다항식의 차수는 2~3차, 다항식 곡선 접합에 사용하는 신호 범위 Δfreq, Δrange는 각각 20 %, 7 % 이상, 그리고 데이터 수는 15개 이상일 경우 공대지 거리측정 정확도에 크게 영향을 주지 않는 것으로 확인했다. 제안한 방법을 이종클러터 환경 및 반사도가 큰 물체의 경우에 대한 시뮬레이션을 바탕으로 정확도를 입증하였고, 이때 γ 보정이 거리 추정 정확도 및 강건성을 높여줌을 확인하였다.





