Ⅰ. 서 론
오늘날 컴퓨터 시스템 내에서 많은 양의 데이터를 고속으로 전송이 가능하도록 하는 방법에 대한 연구가 많이 이루어지고 있다. 최근 고속 메모리 인터페이스인 DDR (Double Data Rate)4나 DDR5에서 크로스토크는 데이터 전송의 주파수 대역 제한에 큰 영향을 미치고 있다. 각 메모리 인터페이스의 신호 전송 속도는 DDR4는 3.2 G~4.8 Gbps, DDR5는 4.8~6.4 Gbps로 굉장히 고속화되었으며, 신호선 개수 또한 증가함에 따라 집적도가 높아져 크로스토크가 신호 품질에 많은 영향을 주게 되었다. 이에 메모리 인터페이스 내부의 크로스토크 저감 방안에 대해 많은 연구가 진행되어 왔다[1]~[3].
하지만 지금까지 소개된 신호선의 크로스토크 감소를 위한 모델링 측면에서의 연구는 부가적인 구조를 통해 해결하거나[4], 비아 스텁(via stub)을 적용[1]하는 등의 구조의 복잡성 및 비용측면에서 효율이 낮다는 단점을 갖고 있었다. 또한 이러한 방법들은 전자기 시뮬레이션 해석 시간이 오래 소요되어 해석 및 분석 측면에서도 불리하였다.
이러한 문제점을 보완하기 위해 본 논문에서는 선로의 모드 분석 및 위상 지연 분석법을 활용하여 선로 간 크로스토크를 줄일 수 있는 비대칭 구조를 지닌 선로의 너비 및 폭을 수식을 통해 도출하는 방법에 대해 제안하였다. 이를 검증하기 위하여 전자기 해석 툴을 통해 결과를 얻고, 대칭 신호선의 크로스토크 분석 결과와 비교를 통해 제안한 방법의 타당성을 입증하고자 한다.
Ⅱ. 크로스토크 저감을 위한상호 커패시턴스 도입 설계기법
메모리 데이터 버스는 그림 1과 같이 DQ(Data Queue) 버스와 DQS(DQ Strobe) 그리고 메모리 컨트롤러로 이루어져 있다. 신호선인 DQ 버스는 32개 혹은 64개의 신호선으로 이루어진 단일종단 평행버스(single-ended parallel bus)이다. 본 연구에서는 DQ 버스의 단일종단 신호선에서의 고속 신호 전송 시 발생하는 크로스토크를 감소시키기 위한 방안에 대하여 연구하고자 한다. 이를 위해서 본 연구에서는 모드 간 위상 지연 감소에 초점을 두어 신호선 구조를 고안하였다.
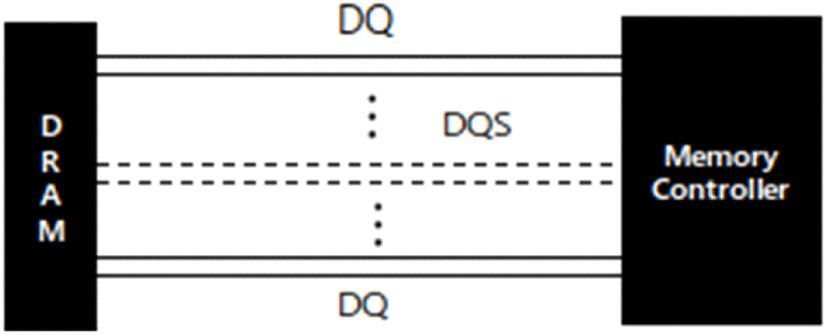
본 연구에서 사용한 3개의 도체로 이루어진 신호선 모델은 한 쌍의 신호선과 그라운드로 구성되어 있으며, 우수 모드와 기수 모드를 가진다. 각 모드의 파라미터는 두 신호선의 상호 인덕턴스 및 상호 커패시턴스와 자기 인덕턴스 및 자기 커패시턴스를 이용해 공식화할 수 있다.
본 장에서는 고속 메모리 인터페이스 내에서 제시된 신호 무결성을 만족하는 신호전달을 위해 수식을 기반으로 비대칭 전송선로의 설계방법을 설명하고자 한다. 먼저 한 쌍의 전송선로에서 형성되는 우수 모드와 기수 모드에 대한 커패시턴스와 인덕턴스 식을 소개하고, 본 연구진에 의해서 기 발표된 선로간의 상호 커패시턴스를 집중소자를 도입하여 증가시키는 방법[3]을 간략히 소개한다. 그리고 본 논문에서 제시하고자하는 비대칭 전송선로를 도입하여 크로스토크를 최소화시키는 새로운 설계방법을 제시하고자 한다.
선로에 신호가 전달될 때는 세 가지의 신호모드가 존재한다. 첫 번째로 신호가 이전 신호를 유지할 경우에는 스테이(stay), 두 번째로 이전 신호가 0에서 1로 변화할 경우에는 상승(rising), 세 번째로 이전 신호가 1에서 0으로 변화할 경우에는 하강(falling)이다. 신호 전달 모드 또한 세 가지로 나눌 수 있으며, 버스 내 한 쌍의 선로에 대해 신호가 같은 위상으로 전파 될 경우 우수 모드, 신호가 서로 반대 위상으로 전파될 경우 기수 모드, 그리고 정적(static) 모드가 있다. 이 때 우수 모드와 기수 모드는 각각 공통 모드와 차동 모드에 대응되는 개념이다[5],[6].
한 쌍의 전송선로 사이에 형성되는 등가 커패시턴스와 등가 인덕턴스를 그림 2에 나타내었다. 여기서 각 파라미터가 의미하는 것은 아래와 같다.
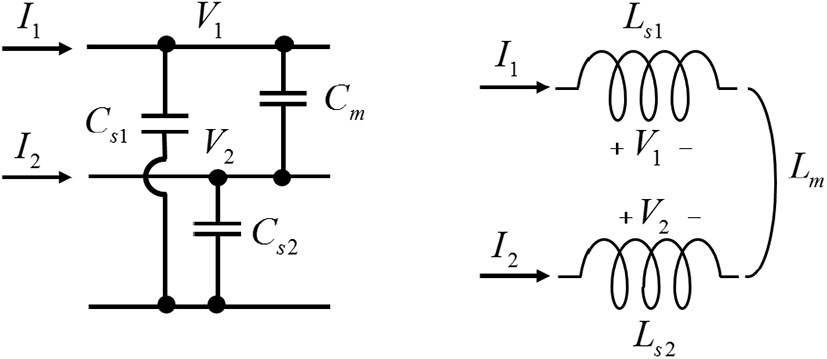
Cs1: 선로1과 그라운드 사이의 자기 커패시턴스 (F/m)
Cs2: 선로2와 그라운드 사이의 자기 커패시턴스(F/m)
Cm: 선로 1과 2 사이의 상호 커패시턴스 (F/m)
Ls1: 선로 1의 자기 인덕턴스 (H/m)
Ls2: 선로 2의 자기 인덕턴스 (H/m)
Lm: 선로 1과 2 사이의 상호 인덕턴스 (H/m)
* 위의 파라미터들은 모두 단위 길이 당 값에 해당함.
식 (1)~식 (3)은 각각 우수 모드에서의 단위 길이 당 커패시턴스와 인덕턴스, 그리고 전파 지연 차이(propagation delay difference)를 선로의 등가 정수소자로 나타낸 것이다. 우수 모드에서는 선로 축의 위치에 따라 동일한 전압을 형성하기 때문에 유효 커패시턴스는 상호 커패시턴스에 의해 감소하게 되며, 전류 또한 항상 같은 방향으로 흐르므로, 전체 인덕턴스는 상호 인덕턴스로 인하여 증가하게 된다.[6]
Ceven: 우수 모드의 단위 길이 당 커패시턴스 (F/m)
Leven: 우수 모드의 단위 길이당 인덕턴스 (H/m)
TDeven: 우수 모드의 단위 길이당 전파 지연 (s/m)
마찬가지로 식 (4)~식 (6)은 각각 기수 모드에서의 커패시턴스, 인덕턴스, 그리고 전파 지연을 선로의 등가 정수소자로 나타낸 것이다. 기수 모드에서 선로 사이의 전압차는 유효 커패시턴스를 상호 커패시턴스 값만큼 증가시키며, 전류는 반대 방향으로 흐르므로 전체 인덕턴스는 상호 인덕턴스로 인해 감소하게 된다.[6]
Codd: 기수 모드의 단위 길이 당 커패시턴스 (F/m)
Lodd: 기수 모드의 단위 길이 당 인덕턴스 (H/m)
TDodd: 기수 모드의 단위 길이 당 전파 지연 (s/m)
식 (3) 및 식 (4)를 통해서 우수 모드는 상호 커패시턴스로 인한 값의 변화가 일어나지 않고, 기수 모드는 상호 커패시턴스로 인해 값의 변화가 일어난다는 점을 알 수 있다. 이는 신호선 사이에 임의의 커패시턴스 성분을 도입하거나 또는 신호선의 구조를 변형하였을 때에 기수 모드의 전파 지연의 변화가 지배적으로 일어날 수 있다는 것을 의미한다.[3]
식 (7)은 두 모드의 전파 지연의 차이를 나타낸 것이다. 실제 선로 디자인에서 통상 가 보다 크기 때문에, 기수 모드의 신호가 우수 모드의 신호보다 먼저 수신단에 도착한다.
ltr: 전송선로의 길이 (m)
ΔTDmode: 단위 길이당 모드 사이의 지연차이 (s/m)
ΔTDtr: 전송선로 길이를 곱한 모드 간 지연차이 (s)
식 (9)는 한 쌍의 커플링(coupling)된 전송선로에서의 보상 커패시턴스에 대한 공식이다. 한 쌍의 전송선로에 단락 커패시턴스 불연속성(shunt capacitance discontinuity)이 존재하게 되면, 추가적인 지연이 존재하게 된다. 식 (9)는 모드 간 전파 지연 차이가 Zodd와 Cc(보상 커패시턴스)에 비례함을 나타냈다. 해당 식들을 사용하여 참고문헌 [3]에서는 한 쌍의 전송선로 사이에 보상 커패시턴스 값을 적용하여 모드 간 지연 차이를 감소시켰다.
주파수 영역에서의 모드 간 위상 차이(Δϕtr)는 식 (11)과 같이 모드 간 지연 차이(ΔTDtr)를 나타내며, 모드 간 지연 차이는 시간 영역에서의 지터(jitter)에 대응한다. 지터는 크로스토크를 유발하는 요인이며, 따라서 모드 간의 위상 차이를 감소시킴으로써 크로스토크를 저감할 수 있음을 알 수 있다. 아울러 주어진 시간영역에서의 지연 차이(ΔTDtr)에 대하여 주파수 영역에서의 위상 차이(Δϕtr)는 주파수가 증가하면 증가됨을 알 수 있다.
본 절에는 식 (9)에서의 보상 커패시턴스(Cc)를 실제 집중 소자(커패시턴스)로 대치하여 본 논문에서 제시하는 지연 차이(ΔTDtr)가 감소함을 확인하고자 한다. 이것에 대한 내용은 본 고가 작성 중인 현재, 아직 출판되지 않은 참고문헌 [3]에서 자세히 기술되어 있으며, 여기에서는 보상 커패시턴스의 유효함을 보이기 위해서 간략하게 이 내용을 소개한다.
그림 3은 크로스토크 저감을 위하여 선로 사이에 커패시터를 놓아 준 모델의 위에서 본 모습과 정면에서의 모습을 나타낸 것이다. 전체 PCB는 50 mm×35 mm의 사이즈를 가지는 기판이다. 또한 한 쌍의 선로(Line 1과 Line 2) 모두 마이크로스트립 선로로서 같은 너비와 두께를 가지며, 임피던스도 50 ohm으로 같다. w=0.335 mm, t=0.04 mm이다. Substrate는 FR-4로, ϵr은 4.3이며 기판 두께는 0.2 mm이다. d=선로 사이의 간격으로 0.295 mm이며, 두 선로 중앙 사이의 거리는 0.635 mm이다. 또한 참고문헌 [3]에서 구한 보상 커패시턴스(Cc) 값은 500 fF이다.
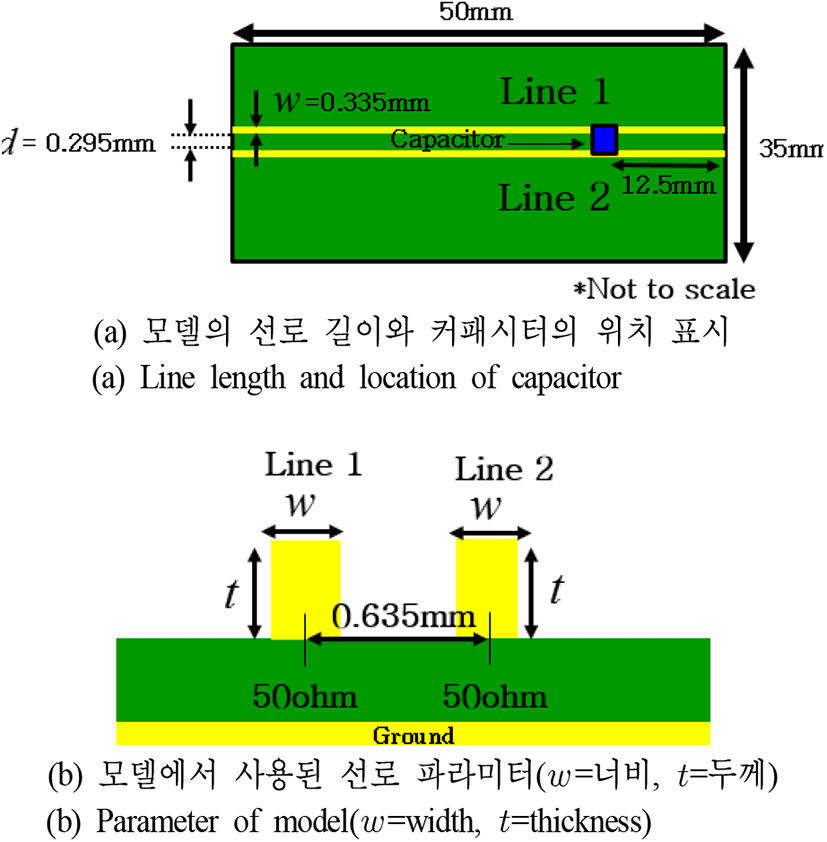
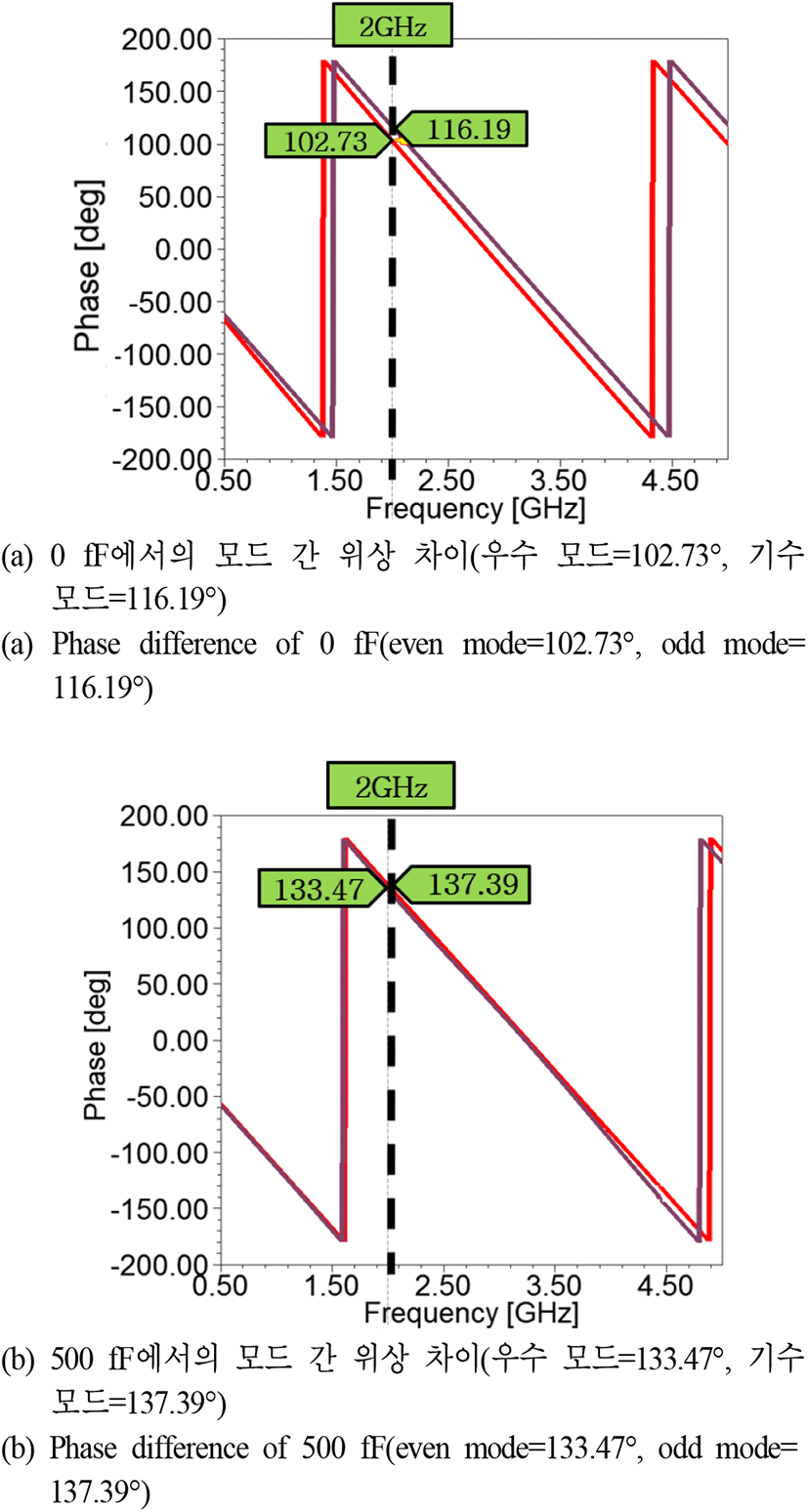
그림 4는 해당 모델의 커패시터 값에 따른 모드 간 위상 차이를 나타낸 전자기장 시뮬레이션 결과이다. 커패시터를 적용하지 않았을 때(0 fF)는 2 GHz에서 모드 간에 약 13.46° 가량의 위상 차이가 나타남을 알 수 있다. 그러나 500 fF의 보상 커패시터를 적용하였을 경우, 모드 간의 위상 차이가 2 GHz에서 3.92° 가량으로 확연히 줄어듦을 확인할 수 있다.
다음 Ⅲ장에서는 집중 커패시턴스 대신에 분포 커패시턴스를 이용하여 크로스토크를 절감시키는 전송선로 구조를 설계 및 시뮬레이션 결과를 보이고자 한다.
Ⅲ. 최적화 기법을 이용한 크로스토크 저감을 위한 비대칭 전송선로 설계
앞서 소개한 전송선로에서의 보상 커패시턴스 공식을 통하여 2-2에서는 한 쌍의 전송선로 사이에 추가적인 집중(lumped) 커패시턴스 값을 더하는 방식으로 크로스토크를 저감시킬 수 있었다. 이에 본 절에서는 분포(distributed) 커패시턴스 값을 더하여 크로스토크를 저감할 수 있는 선로 설계 방안을 제시하고자 한다.
식 (7)에서 알 수 있는 점은 과 의 차이를 줄이는 것이 모드 간 지연 차이를 줄일 수 있다는 것이다. 따라서 선로 간 Cm을 증가시킴으로써 크로스토크를 저감할 수 있다는 점에 착안하여 한 쌍의 커플링된 비대칭 선로를 설계할 수 있다. 이러한 조건을 만족시키는 비대칭 전송선로의 구조를 찾기 위하여 식 (7)의 최적화 과정을 진행하도록 한다.
또한, 구해진 너비에 맞추어 선로 간 임피던스가 깨지지 않도록 기준 선로와 유사한 임피던스를 갖게 하는 선로 두께를 구한다. 예를 들어, 기준 선로가 50옴이면 변경 선로도 50옴에 가까운 임피던스 값을 갖도록 한다.
제안한 비대칭 선로의 파라미터 설정 방법을 검증하기 위하여 Ⅲ에서는 전자기 시뮬레이션을 활용하여 최적화를 진행하고, 결과를 보이도록 하였다.
앞서 소개한 비대칭 선로의 크로스토크 저감 효과를 검증하기 위하여 먼저 대칭선로에 대한 2차원 해석 결과를 보이고자 한다. 대칭선로의 모델링 및 해석 결과와 모드 간 전파 지연 차이를 보이며, 크로스토크를 최소화하는 비대칭 선로를 설계 및 해석하여 두 결과를 비교하고자 한다.
본 절에서 모델링한 대칭선로는 2-2의 그림 3에서와 같은 너비와 높이가 같은 모델을 사용하였다. 해당 모델은 ANSYS 사의 Q2D를 통해 2차원 전자기 시뮬레이션을 수행하였고, 2 GHz에서의 결과를 출력하였다.
이에 대한 2차원 해석 결과를 표 1에 나타내었으며, 식 (7) 및 식 (11)에 표 2의 해석 결과와 선로 길이 50 mm를 대입하여 얻은 모드 간 전파 지연(ΔTDtr)의 결과는 25 ps이다.
| Inductance (nH/m) | Capacitance (pF/m) | |
|---|---|---|
| Ls1, Cs1 | 303.9 | 105.32 |
| Lm, Cm | 44.62 | 6.9 |
| Inductance (nH/m) | Capacitance (pF/m) | |
|---|---|---|
| Ls1, Cs1 | 315.79 | 102.66 |
| Lm, Cm | 43.09 | 7.66 |
크로스토크 저감을 위한 비대칭 선로 설계를 위하여 ANSYS 사의 HFSS에 내장되어 있는 전자기장 시뮬레이션과 연동하여 결과를 낼 수 있는 최적화 툴박스를 사용하여 최적화를 진행하였다.
최적화에 사용한 알고리즘은 연속 비선형 프로그래밍(sequential nonlinear programming: SNLP)이다. SNLP는 연속적이며, 최적화 상태를 가장 최신의 최적값으로 업데이트해 주고 그것을 반복하는 알고리즘이다[7].
최적화 시 설정한 조건을 정리하면 다음과 같다.
식 (7)의 ΔTDmode 값을 500 ps/m보다 작은 값을 갖도록 설정하였다. 대칭 선로의 ΔTDmode값이 500 ps/m 였기 때문에 그보다 더 작은 값을 갖도록 설정하였다.
한 쌍의 선로의 임피던스 모두 선로 간의 임피던스가 깨지지 않도록 50옴±3옴으로 설정하였다.
아울러 ΔTDmode 계산 시 사용한 식 (7)은 대칭 선로 적용이 되는 수식이나, 본 연구에서는 식 (7)이 미소한 비대칭인 경우에도 사용 가능하다는 가정하에 최적화를 진행하였다. 그림 5는 최적화 시에 사용한 파라미터들의 변수를 나타낸 것이다. w1,w2는 각 선로의 너비이고, t1,t2는 각 선로의 두께이다. 이 파라미터들을 변경시켜 최적의 ΔTDmode값을 가지는 선로의 너비와 두께를 선정하도록 하였다.
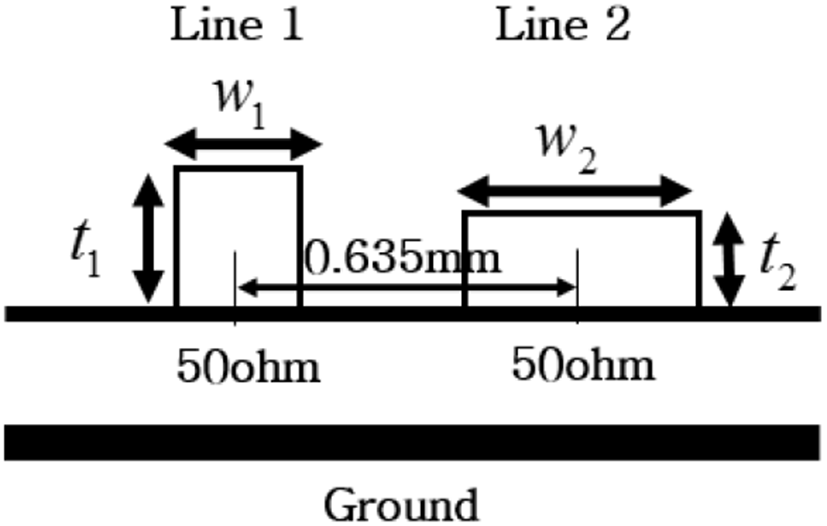
최적화 과정을 통해 w1=0.345 mm, w2=0.413 mm, t2=0.0158 mm, t2는 0.0136 mm가 얻어졌다. 이때 얻어진 ΔTDmode값은 400 ps/m이었고, 이와 같은 너비와 두께를 가지는 선로 임피던스는 각각 52, 47옴으로 확인되었다. 선로 길이(ltr)는 50 mm로 하였으며, 기판 물성과 두께 또한 3-2에서와 동일하게 설정하여 시뮬레이션을 수행하였다.
표 2에는 비대칭 마이크로스트립 선로의 2차원 해석 결과를 나타내었으며, 식 (7)과 식 (11)에 표 2의 해석 결과와 선로 길이 50 mm를 대입하여 얻은 모드 간 전파 지연의 결과(ΔTDtr)는 20 ps(=400 ps/m×0.05 m)이다.
앞서 해석한 대칭 신호선의 2 GHz에서의 모드 간 위상 지연 결과와 최적화된 비대칭 선로의 모드 간 위상 차이를 비교하였을 때, 약 5 ps의 전파 지연 차이(ΔTDtr)가 개선되었음을 확인할 수 있다.
Ⅳ. 크로스토크 저감을 위한 비대칭 전송선로의 3차원 전자기장 시뮬레이션
3-2에서는 Q2D를 이용한 2차원 최적화 과정으로 크로스토크 저감이 가능한 비대칭 전송선로의 구조를 설계하였다. 이제 이 구조를 3차원 모델에 적용하여 전자기장 시뮬레이션을 진행하였다.
비대칭 이론을 적용한 선로의 결과 이전에, 결과 비교를 위하여 대칭 선로의 시뮬레이션 결과를 먼저 보였다.
시뮬레이션에서 사용한 대칭 선로는 2-2의 그림 3에서 소개되었던 모델에서 커패시터만 빠지고 기판의 크기와 두께, 선로의 너비와 폭이 모두 같은 모델이다.
그림 6은 대칭 신호선 구조의 모드 간 지연 차이와 아이 다이어그램을 나타낸 것이다. 모드 간 지연 차이는 ANSYS 사의 HFSS를 사용하여 얻은 결과이며, 아이 다이어그램은 Agilent 사의 ADS 프로그램을 사용하여 나타내었다. 2 GHz에서 대칭 신호선 구조의 모드 간 위상 차이는 그림 4(a)에서와 같이 약 13.46°이며, 그림 7과 같이 지터는 23.7 ps임을 확인할 수 있다.
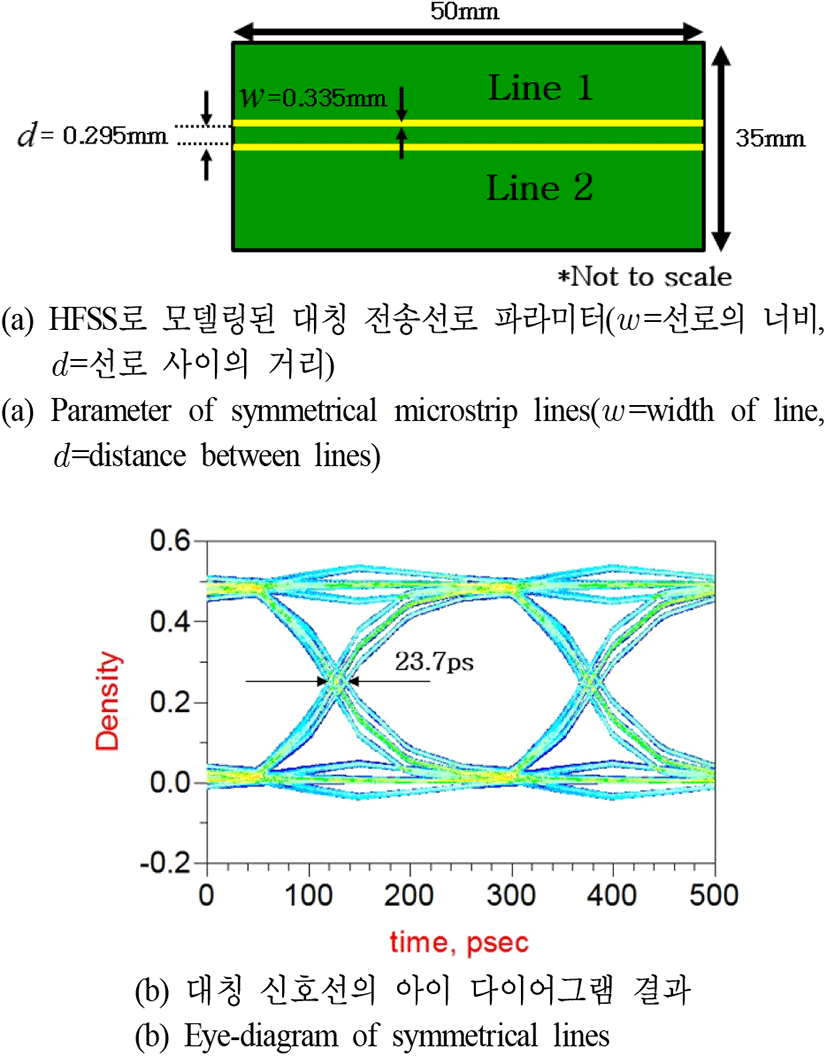
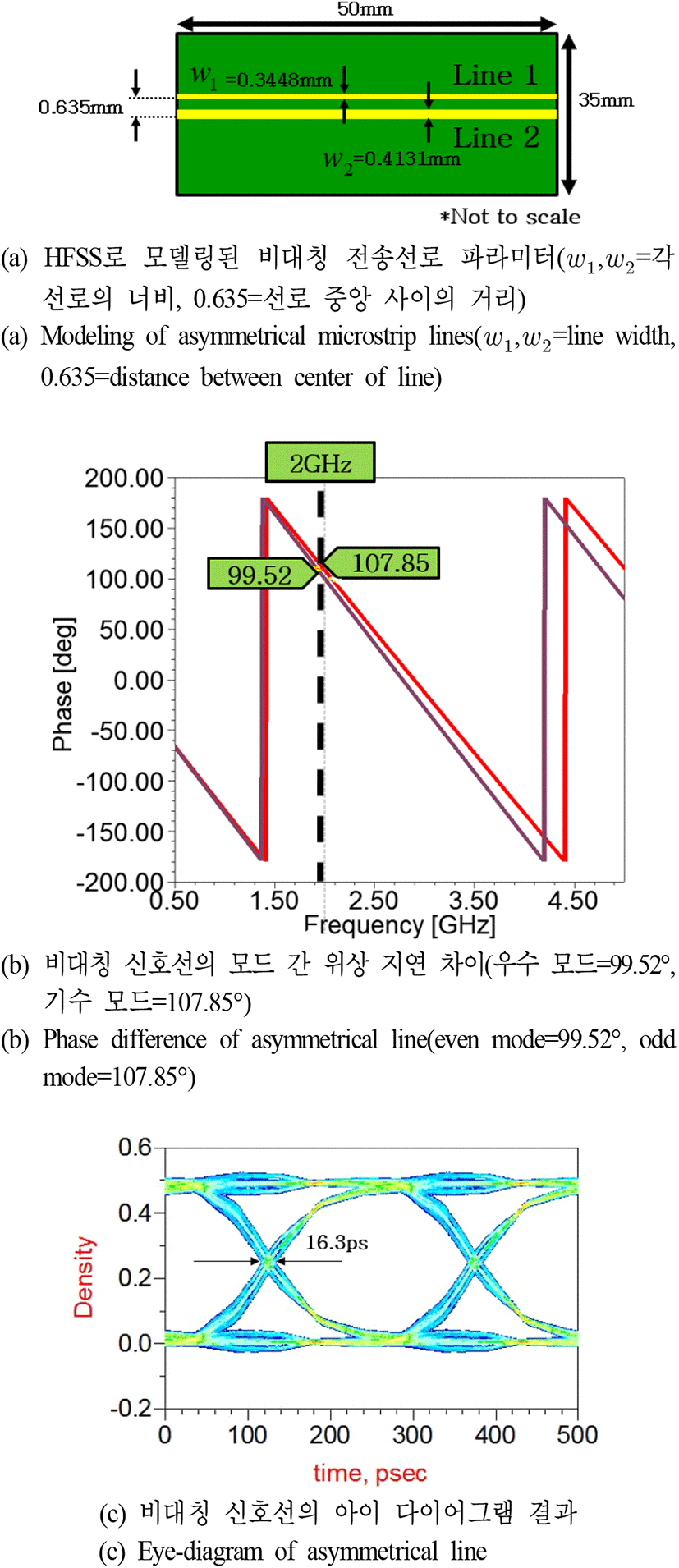
그림 7(a)는 3-2에서 제시한 비대칭 선로를 3차원 구조로 설계한 모델의 파라미터를 나타낸 것이다. 따라서 w1=0.345 mm, w2=0.413 mm, t2=0.0158 mm, t2는 0.0136 mm이며 기판의 가로길이와 세로길이는 그림 6(a)와 동일하다. 그림 6(b)는 본 논문에서 제시한 비대칭 신호선 구조의 모드 간 지연 차이이며, 약 8.33°인 것을 확인할 수 있다. 그림 6(c)는 해당 구조의 아이 다이어그램이며, 지터가 16.3 ps임을 확인할 수 있다.
그림 6과 그림 7의 비교 결과를 표 3에 정리하였다. 단 대칭 신호선 구조의 위상 지연 결과는 그림 4(a)와 같다. 표 3을 통해 비대칭 신호선 구조의 위상 지연 결과가 5.13°만큼 개선됨을 확인할 수 있다. 또한 대칭 신호선 구조일 때는 23.7 ps의 지터를 가지고, 비대칭 신호선 구조의 경우 16.3 ps으로 지터가 감소한다. 이를 통해 본 논문에서 제시한 비대칭 신호선 구조가 대칭 신호선 구조에서보다 개선된 신호 무결성을 가짐을 확인할 수 있다.
| Symmetrical | Asymmetrical | |
|---|---|---|
| Phase difference (°) | 13.46 | 8.33 |
| Jitter (ps) | 23.7 | 16.3 |
크로스토크 저감 효과를 직접적으로 보이기 위하여 본 논문에서 제시한 세 가지 구조인 집중소자를 이용한 구조, 대칭 전송선로, 비대칭 전송선로의 목표 주파수인 2 GHz에서의 FEXT(Far End Crosstalk)을 비교한 것을 그림에 나타내었다. 그림 8에서 확인할 수 있듯이, 비대칭 전송선로가 대칭 전송선로보다 개선된 크로스토크를 가짐을 알 수 있다. 집중소자를 이용한 구조가 가장 낮은 크로스토크를 가지며, 대칭 전송선로가 가장 높은 크로스토크를 가짐을 알 수 있다.
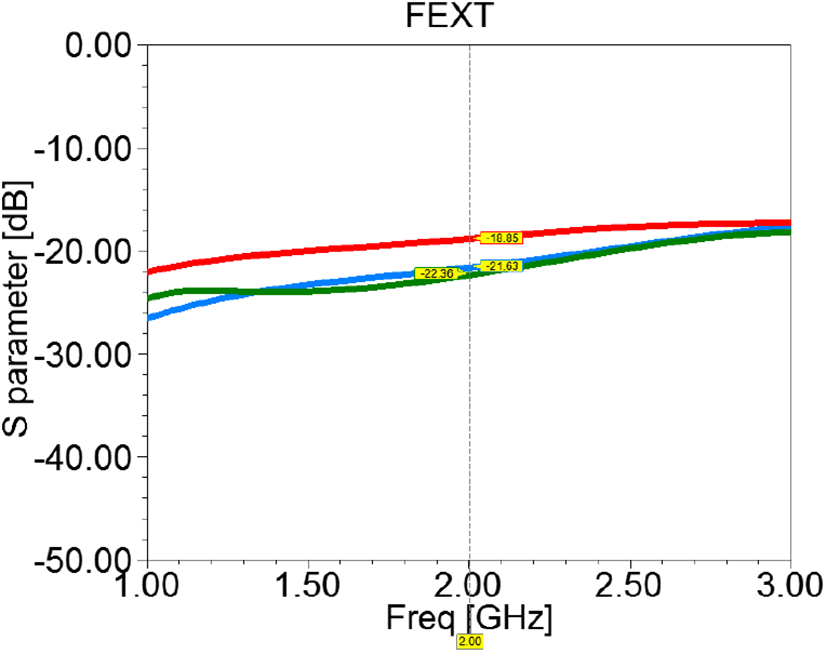
2 GHz에서의 각 구조별 산란계수 값을 표 4에 정리하였다. 대칭 전송선로는 −18.85 dB, 집중소자를 이용한 구조는 가장 낮은 −22.37 dB의 FEXT를 가지며, 본 논문에서 제시한 비대칭 전송선로는 −21.64dB의 FEXT를 가지는 것을 알 수 있다.
| Lumped capacitor | Symmetrical | Asymmetrical | |
|---|---|---|---|
| FEXT (dB) | −22.37 | −18.85 | −21.64 |
Ⅴ. 결 론
본 논문에서는 제안된 비대칭 전송선로 구조를 이용하여 모드 간의 위상 차이를 줄일 수 있음을 보였다. 즉, 기수 모드 신호 지연을 우수 모드의 신호 지연에 근접하게 함으로써 위상 차이가 줄어들게 된다. 이러한 위상차이의 최소화는 두 선로의 상호 커패시턴스 값을 증가시킴으로써 가능함을 보였다. 이러한 조건을 만족시키는 비대칭 전송선로의 구조를 찾기 위하여 ANSYS사의 HFSS 최적화 툴박스를 이용하였으며, 그 결과, 선로 너비와 두께는 w1=0.3448 mm, w2=0.4131 mm, t2=0.0158 mm, t2는 0.01356 mm를 얻었다. 또, 이러한 구조에서 각 선로의 특성 임피던스가 50옴±3옴 범위 내에 존재한다는 것도 확인하였다.
이와 같이 구한 선로의 너비와 두께를 적용한 모델을 3차원 시뮬레이션에 적용한 결과, 대칭 선로와 비교하였을 때 비대칭 전송선로가 모드 간 지연 차이에서는 약 13.46°에서 8.33°으로 감소함을 확인하였고, 또한 지터는 23.7 ps에서 16.3 ps로 약 7.4 ps만큼 개선된 것을 확인할 수 있었다. 이 결과를 통해서 본 논문에서 제시한 비대칭 전송선로 구조는 대칭 전송선로 구조보다 개선된 신호 품질을 가짐을 알 수 있었다.
메모리 버스의 PCB 상의 비대칭 선로의 실제 구현에 있어서 선로 두께를 조절하는 공정 기술이 중요한 점이라 할 수 있을 것이다. 제작 업체를 통하여 확인해 본 바 구리 층 두께를 다르게 하는 공정에는 추가 공정을 통하여 실제 제작이 가능함을 확인하였다. 다만 실제 제작에 필요한 공차를 고려해야 할 것이다. 기본적으로 크로스토크를 최소화하는 구조는 본 논문에서 제시하는 구조 이외에도 여러 개가 있을 수 있다고 사료되며(유일해가 아님), 추후에 제작이 가능하면서 크로스토크를 최소화하는 구조를 찾아내어 본 논문에서 제시한 방법의 타당성을 실험으로 보일 예정이다. 또한 이러한 개념은 3개 이상의 선로에서도 새로운 모드의 정의와 함께 확장되어 적용될 수 있을 것으로 사료된다.




