Ⅰ. 서 론
레이다의 개발 추세에 맞추어 최근에 개발되는 많은 레이다의 안테나는 능동 위상 평면 배열의 형태로 개발되고 있다. 이러한 능동 위상 평면 배열은 잘 알려진 바와 같이 개별적인 복사 소자와 이에 연결되어 있는 TRM (transmit-receive module)으로 구성되고, 그 뒷단이 모두 RF 급전기로 합쳐진 다음, 수신기와 ADC(analog to digital converter) 등이 차례로 연결되는 고전적인 형태부터, 전체 배열을 임의의 부분으로 나누어 각 부분을 RF 급전기로 묶어 형성된 여러 부배열에 각각의 수신기와 ADC를 연결하여 신호처리단에서 디지털 빔형성을 수행하는 하는 부배열 구조, 더 나아가서는 각 TRM 뒷단에 각각의 수신기와 ADC를 구성하여 각 소자별로 디지털 빔형성을 수행할 수 있는 디지털 레이다[1]~[3]. 구조로 발전해 가고 있다.
위에서 언급한 어떠한 형태의 능동위상배열 구조를 선택하더라도 빔형성의 관점에서 보면, 송신빔의 경우에는 대부분, 배열 전체에 동일한 출력의 TRM을 사용하여 균일 분포(uniform distribution)의 진폭 가중치가 얻어지고, 이에 따라 빔폭이 좁고 이득은 높지만 최대 부엽이 비교적 높은 빔이 형성되는데, 잘 알려져 있는 바와 같이 직사각형 평면의 경우 약 −13 dB, 원형 평면의 경우 약 −18dB의 최대 부엽 수준을 나타낸다[4]. 이러한 송신빔의 경우에, EIRP(effective isotropic radiated power)에 일부 손해를 감수하더라도 최대 부엽 수준을 낮추기 위해서는, 일부 모듈들의 출력을 off하여 평면 배열의 유효 면적(effective aperture)을 변화시켜 유효 진폭 분포를 최적화하는 thinned array를 구성하는 방법[5]과, 균일한 송신 출력에 따른 진폭 가중치는 변화시킬 수 없으므로, 각 배열소자채널의 위상을 최적화 하는 방법 등을 주로 사용하게 된다.
한편, 수신빔의 경우에는 위에서 언급한 어떠한 형태의 능동위상배열 구조를 취하든지 진폭과 위상을 모두 조정할 수 있기 때문에 빔형성의 자유도가 훨씬 높다. 물론 위에 언급한 구조에 따라 진폭과 위상을 조절하기 위해 RF 하드웨어(가변 감쇄기/위상변위기)를 사용하기도 하고, 또는 신호처리단에서의 디지털 빔형성으로 이를 구현할 수도 있어서 구현 방법과 성능에 있어서 차이는 있지만, 진폭과 위상을 모두 조정할 수 있는 이러한 자유도 때문에, 특히 수신빔의 경우에는 요구사항에 따라 특정영역에 null 또는 매우 낮은 부엽을 형성하거나, 특정 영역별로 다른 부엽 수준을 구현하도록 하는 등의 매우 다양하고 특수한 빔형성 기법들이 지속적으로 연구되어 왔다[5].
하지만, 일반적으로 레이다에서 사용하는 가장 기본이 되는 모드의 수신빔은 균일한 위상 분포에 최적의 진폭 분포를 통해 얻어지는 복사 패턴을 가지며, 그 최대 부엽 수준이 특정 수준을 넘지 않는 저부엽 펜슬빔으로 선정되는 경우가 많다. 이를 위해서 실제로 가장 많이 사용되는 진폭 가중치는 Taylor 가중치[5]이며, 직사각형 형상의 평면 배열인 경우, 진폭 가중치 분포를 수평/수직 방향 각각의 선배열 Taylor 가중치를 곱하여 사용하고, 형상이 원형인 평면 배열의 경우에는 원형 Taylor 분포를 통해 원하는 부엽 수준 성능을 구현할 수 있다.
그러나 실제 레이다 시스템에 사용하는 평면 배열을 개발하는 경우에는, 평면 배열 장착 공간의 제한 및 배열 구조를 구성하는 TRM의 모듈화, 제작/조립 및 방열, 실제 운용 및 정비 등 통합적 관점에서의 수많은 고려 사항 때문에, 직사각형 등의 정형화된 면 형상보다는 그림 1과 같이 변형된 형태의 평면 배열 면 형상(planar array aperture shape)을 가지는 경우가 많다. 대개 이러한 형상의 배열 면에도 위에서 언급한 바와 같은 일반적인 Taylor 진폭 가중치를 적용한다. 하지만, 이렇게 보통의 Taylor 진폭 가중치를 사용하면 배열 형상에 따라서는 전공간의 최대 부엽 수준이 설계하고자 하는 부엽 수준과 꽤 차이가 나고, 설계 수준 대비 상당히 높은 값을 나타내는 경우도 있다.

본 논문에서는 그림 1에서 보이는 바와 같이 종합적 요구사항을 고려하여 선정된 다양한 형상의 배열 면을 이용하여 수신빔을 형성할 때, 안테나 주빔 영역 이외의 전 공간에서 원하는 부엽 수준을 나타내는 최적의 진폭 분포를 구해내는 방법을 제시하였다. 참고문헌 [6]에서 제시한 선배열(linear array) 복소 가중치(complex weight)를 최적화 하는 방법을 응용하여, 임의의 형상이지만 수평/수직 선대칭인 면배열 및 임의의 형상이지만 면배열 중심에 대해 점대칭인 면배열 두 가지 경우에 대해, 복소 가중치가 아닌 원하는 진폭 가중치를 구하는 방법에 대해 기술하고, 각각의 경우에 대해 최적화한 진폭 가중치를 적용하여 얻어지는 빔패턴의 최대 부엽 수준을 보임으로써 제안한 방법의 타당성을 검증하였다.
Ⅱ. 부엽 수준 최적화 알고리즘
먼저 그림 1의 다양한 배열 형상에 대해 일반적으로 적용되는 Taylor 진폭 분포를 적용했을 때 나타나는 최대 부엽 수준에 대해 표 1에 정리하였다. 표 1에서 보듯이 원하는 부엽 수준을 달성하기 위한 일반적인 진폭 가중치인 Taylor 가중치를 적용했음에도 불구하고, 공간상에서 나타나는 최대 부엽 수준은 이보다 높은 수준임을 알 수 있다.
| 배열 형상 | 전공간 최대 부엽 수준 | 적용 가중치 |
|---|---|---|
| 배열#1 | −27.4 dB | Taylor 28 dB |
| 배열#2 | −22.3 dB | Taylor 23 dB |
| 배열#3 | −28.1 dB | Taylor 35 dB |
| 배열#4 | −28.2 dB | Taylor 35 dB |
| 배열#5 | −30.3 dB | Taylor 35 dB |
물론, 이러한 최대 부엽 수준을 낮추는 가장 쉬운 방법은 기준보다 더 낮은 부엽수준을 제공하는 Taylor 가중치를 사용하는 것이다. 그러나 이 경우, 필요 이상으로 주빔의 빔폭을 넓게 하고, 안테나 이득을 감소시키게 되는 단점이 있다. 이에 따라 본 논문에서는 원하는 부엽 수준 달성을 위해 일반적으로 적용하는 기준 진폭가중치를 가능한 변화시키지 않으면서, 목표로 하는 최대 부엽수준을 달성하는 최적화된 가중치 분포를 구하는 절차를 기술하고자 한다.
일단, 본 논문에서 고려하는 평면 배열은 기본적으로 참고문헌 [6]에서와 동일하게 다음과 같은 조건을 만족한다고 가정한다. 첫째로, 주어진 평면 배열은 좁은 상대 대역폭을 가지며, 둘째로, 복사소자(radiator)들 간의 상호 간섭(mutual coupling)은 없는 것으로 가정한다. 셋째로는, 각 복사소자들의 개별적인 방사 패턴은 동일하지 않아도 된다. 넷째로, 본 논문의 목적은 평면 배열의 최적 진폭 가중치를 구하는 데에 있으므로, 주빔의 방향은 배열 면에 수직 방향(boresight)으로 가정해도 일반성을 잃지 않는다.
이러한 조건을 바탕으로, U-V공간에서 특정 방향 (u,v)에서 입사하는 평면파에 대해 복소 가중치 w를 적용해서 얻어지는 평면배열의 수신 출력 s(u,v)는 다음과 같이 나타낼 수 있다.
식 (1)에서 a(u,v)는 (u,v)방향에서 입사하는 신호 벡터이며, H는 Hermitian transpose를 뜻한다. 여기서 신호 벡터 a(u,v)는 다음과 같이 나타낼 수 있다.
여기서 (xi,yi)는 평면 배열의 i번째 복사소자의 좌표이며, gi(u,v)는 i번째 복사소자 패턴이다. 식 (2)는 일반적으로 평면 배열에 입사하는 신호 벡터의 표현이지만, 평면 배열의 형상이 위에서 언급한 바와 같은 대칭성을 나타낼 경우 조금 더 간략한 형태로 나타낼 수 있다.
첫 번째로, 평면 배열이 임의의 형상을 취하고 있지만, 수평/수직 방향으로 각각 대칭인 면배열을 살펴 보기로 한다.
이 경우는 그림 2에서 보는 바와 같이 주로 사각 격자(rectangular grid) 구조를 가진 평면 배열로, 배열의 중심을 원점으로 놓았을 때, 제 1사분면에 좌표가 존재하는 복사소자와 그 좌표가 대칭되는 복사소자가 제 2, 3, 4사분면에 각각 존재하고, 이에 따라 좌표가 대칭인 복사소자들의 진폭 가중치를 동일하게 적용하는 것이 합리적이며, 해당 복사소자들의 소자 패턴(element pattern)은 동일하다 할 수 있다. 이러한 전제 하에 식 (1)과 식 (2)로 주어지는 평면 배열의 수신 출력은 다음과 같은 식 (3)으로 간략하게 나타낼 수 있다.

식 (3)에서 (xn,yn)은 제 1사분면에 존재하는 복사소자의 좌표이다. 만일 식 (3)에서 wn이 진폭 가중치이고, 복사소자 패턴 gn(u,v)를 실수로 가정하면, 전체 수신 출력 s(u,v) 역시 실수가 됨을 알 수 있다. 또한 복사소자 패턴 gn(u,v)가 U-V평면에서 U축, V축에 대해 모두 대칭이면, 수신 출력 s(u,v) 역시 U-V평면에서 U축, V축에 대해 모두 대칭임을 알 수 있다.
두 번째로는, 평면 배열이 임의의 형상을 취하고 있지만, 면배열 중심에 대해 점대칭인 면배열에 대해 살펴보기로 한다.
이 경우는 그림 3에서와 같이 주로 삼각 격자(triangular grid) 구조를 가진 평면 배열이 해당된다. 잘 알려진 바와 같이 삼각 격자 구조는 평면형 위상 배열에 요구되는 빔조향 범위를 달성하기 위한 배열 소자의 간격을 사각 격자보다 상대적으로 넓힐 수 있어서[7], 빔조향 범위가 커야 할 경우의 평면 배열 구조에서는 대부분 이러한 삼각 격자 구조가 사용된다. 배열 소자의 간격을 넓히는 것은 동일 면적에 필요한 TRM의 개수를 줄일 수 있고, 방열에 도움이 되는 등 여러 가지 장점이 많기 때문이다. 그림 3에서 보면, 이러한 격자 구조를 가지는 평면 배열은 제 1사분면에 좌표가 존재하는 복사소자와 그 좌표가 대칭되는 복사소자는 제 3사분면에, 제 2사분면에 좌표가 존재하는 복사소자와 그 좌표가 대칭되는 복사소자는 제 4 사분면에 존재함을 알 수 있다. 이를 이용하면 평면 배열의 수신 출력은 식 (4)와 같이 간략화할 수 있음을 알 수 있다.
식 (3)에서와 마찬가지로 식 (4)에서도, wn이 진폭 가중 치이고, 복사소자 패턴 gn(u,v)를 실수로 가정하면, 이 경 우의 전체 수신 출력 s(u,v) 역시 실수가 됨을 알 수 있다.
위에서 언급한 두 가지 대칭성을 지닌 평면 배열 형태에 대한 수신 출력의 수식 표현을 전제로, 원하는 부엽 수준 구현을 위해 진폭 가중치 최적화를 위한 절차를 기술하고자 한다.
먼저, 일반적으로 사용할 수 있는 Taylor 분포 등의 전형적인 진폭 가중치 w0을 적용하여, 식 (3) 또는 식 (4)를 통해 해당 평면 배열의 복사 패턴을 계산하고, 이로부터 전체 U-V 평면 상에서의 부엽 첨두치(peak)들의 값을 계산한다. 계산 결과 원하는 수준보다 높은 부엽 첨두치가 존재하면, 이를 낮추기 위해 원래의 진폭 가중치에 미소값을 가지는 추가 가중치 Δw를 더한다. 이 때, Δw가 만족해야 하는 조건은 참고문헌 [6]에 나타난 바와 같이 다음의 식 (5), 식 (6)과 같이 설정한다.
식 (5), 식 (6)에 대한 의미를 설명하기 전에, 일단 이 식들은 잘 알려진 선형 제약 최소 제곱 (linearly constrained least square)의 최소화 문제임을 알 수 있으며[8], 잘 알려진 바와 같이 이러한 문제의 해는 행렬을 이용한 해석적인 표현 및 풀이가 가능하다[6]. 먼저, 식 (5)는 공간 상에서 주빔을 제외한 부엽 영역에서 진폭 가중치 변화 Δw에 의한 전체 부엽 전력 증가 합을 최소화하기 위함이다. 이에 따라 식 (5)에서 은 부엽 영역을 균일하게 나누었을 때 l번째 부엽 방향 신호벡터를 나타낸다. 이 때 만족해야 하는 선형 제약 조건(linear constraints)들은 식 (6)으로 나타내었다. 식 (6)의 첫 번째 조건은 주빔의 빔조향 방향이 진폭 가중치 변화 Δw에 의해서 바뀌면 안 되기 때문에 주어진 조건이며, 이에 따라 as는 주빔 방향 신호벡터를 나타낸다. 두 번째 조건은 주빔의 빔조향 방향에서 패턴이 극대값을 가지도록 제약하는 조건[9]이므로, 및 는 각각 주빔 방향 신호벡터를 u,v 방향으로 편미분치를 취한 벡터가 된다. 한편, 식 (6)의 세 번째 조건이 원하는 바와 같이 부엽 수준을 감소시킬 수 있는 조건이 된다. 원하는 부엽 수준의 선형값을 ϵ이라 하면, 원래 가중치에 Δw을 더함으로써 ϵ을 넘는 부엽 첨두치들이 발생하는 방향에서 부엽 첨두치의 선형값이 ϵ이 되도록 한다. 즉, 원래 가중치에 의해 ϵ을 넘는 i번째 부엽첨두치를 나타내는 방향의 신호 벡터를 ai라 하고, 이 때의 복소 패턴 값을 ci라 하면 다음의 식 (7)을 만족해야 한다.
식 (7)을 수학적으로만 살펴보면 fi는 복소평면 상에서 중심이 −ci이고 반지름이 ϵ인 원위의 모든 값을 취할 수 있으나, 참고문헌 [6]에서 제시한 바와 같이 fi의 절대치가 가장 작도록 정하면 fi는 다음 식과 같이 표현할 수 있다.
한편, 이러한 식을 통해서 조절 가능한 부엽 첨두치의 개수 M은 주어진 선형 제약 조건의 개수가 3개이므로, Δw의 차원(dimension)을 N’ 이라 할 때 (N’ − 3) 이하이어야 함을 알 수 있다. 이에 따라 ϵ을 넘는 부엽 첨두치가 (N’ − 3)개를 초과하면 부엽 첨두치의 크기 순으로 (N’ − 3)개만 선택하여 Δw를 구해야 한다.
이러한 점에 유의하여 잘 알려진 해석적 방법에 의하여 식 (5)의 해 Δw를 구해내면, 새로운 가중치 w’ = w0 + Δw가 얻어진다. 그러나 이러한 새로운 가중치에 의해 얻어진 패턴은 원하는 값 대비 부엽 수준이 높았던 M개의 부엽 위치에서는 정확하게 원하는 부엽 수준을 만족하지만, 그 이외의 위치에서는 다른 부엽 수준을 나타낼 수 있다. 이 때문에 모든 부엽 영역에서 목표로 하는 부엽 수준을 만족시키기 위해서는 위와 같은 과정을 반복하여 수행해야 하고, 이러한 과정을 통해 결국에는 원하는 부엽수준을 제공하는 수렴한 최적 가중치를 얻을 수 있다[6].
여기에서 몇 가지 살펴봐야 할 점은 다음과 같다. 첫째로, 우리가 얻고자 하는 새로운 가중치는 진폭 가중치이므로, 위의 과정을 통해 얻어진 최종 최적화된 가중치가 실수값인지 확인해 볼 필요가 있다. 참고문헌 [6]에서와 같이 식 (1), 식 (2)를 그대로 사용해야 하는 일반적인 경우에는, 각 반복 과정에서 얻어지는 Δw는 당연히 복소값(complex value)을 가지게 된다.
만약 평면 배열의 형태가 대칭성이 전혀 없는 임의 형태의 비정형 면배열의 경우에는 식 (1), 식 (2)를 그대로 사용해야 하고, 이에 따라 Δw가 복소값을 가지게 되므로 각 반복 과정에서 Δw를 구한 다음, ± |Δw|값 중에 복소 Δw에 더 가까운 것을 원래 가중치에 더함으로써 새로운 진폭 가중치를 얻을 수 있다. 하지만 본 논문에서 제시한 것처럼 그림 2나 그림 3과 같은 대칭성을 지닌 평면 배열의 빔패턴은 식 (3)이나 식 (4)와 같이 주어지므로, 이 경우, 식(5), 식 (6), 식 (8)은 모두 실수로 구성된 식이 되고, 우리가 원하는 대로 Δw는 실수값으로 해가 주어짐을 알 수 있다.
두 번째로는, 참고문헌 [6]에 언급한 바와 마찬가지로, Δw를 구하기 위해서는 식 (5)의 행렬 Asl의 역행렬을 계산해야 하는데 이 때, 행렬 Asl의 조건수(condition number) 가 나빠질 수 있으므로, 행렬 Asl의 주대각 원소(diagonal element)에 적절한 양의 값을 더해주는 diagonal loading[10]을 적용하였다.
또한 반복적으로 식 (5)의 해를 구하면서, 식 (6)의 선형 조건을 적용함에 있어 각 조건들이 서로 독립적이어야 하는데, 그렇지 못한 경우 수치 계산 시 문제가 발생할 수 있으므로, 참고문헌 [6]에서 제시한 바와 같이 QR decomposition을 사용하여 중복된 조건을 삭제함으로써, 안정적으로 수치 계산을 수행할 수 있도록 하였다.
Ⅲ. 부엽 수준 최적화 시뮬레이션 결과 비교
그림 1의 다양한 배열 형상 및 구조에 대한 모든 패턴 계산 및 시뮬레이션은 MATLAB으로 구현하였으며, Ⅱ장에서 제시한 부엽 수준 최적화 알고리즘을 이용하여 최적화한 진폭 가중치 분포(Opt w)를 적용했을 때의 빔폭, 지향도, 최대 부엽 수준 등의 빔 특성을, 기준 가중치(w0) 및 최대 부엽 수준 규격을 달성하기 위해 과도한 테이퍼링(tapering) 가중치(w1)를 적용했을 때의 빔 특성과 비교하여 표 2에 정리하였다.
표 2에서 적용한 기준 가중치 w0은 원하는 부엽 수준에 해당하는 방위각, 고각 방향 Taylor 가중치에 의해 합성되는 2차원 진폭 가중치이며, 가중치 w1은 방위각, 고각 방향으로 좀 더 낮은 부엽 수준을 제공하는 Taylor 가중치를 2차원으로 합성한 것으로, 전 공간 최대 부엽 수준을 원하는 수준으로 맞출 수 있도록 한 가중치이다. 물론 Opt w는 본 논문에서 제시한 방법으로 최적화된 가중치를 나타낸다. 표 2에서 전 공간 최대 부엽 수준 항목을 살펴보면 w1과 Opt w 가중치를 적용했을 때, 원하는 부엽 수준(−28 dB, −23 dB, −35 dB, −35 dB, −35 dB)을 만족하고 있음을 알 수 있다. 이러한 전제 하에 방위각, 고각 빔폭 및 지향도 항목을 살펴보면 두 가중치를 적용한 결과에 차이가 있음을 알 수 있다. 이를 좀 더 쉽게 확인하기 위해 그림 4에서는 기준 가중치 w0을 적용했을 때의 빔폭 대비 w1과 Opt w 가중치를 적용했을 때의 빔폭의 증가율을 비교하였고, 그림 5에서는 기준 가중치 w0을 적용했을 때의 지향도에 비해 나머지 가중치를 적용했을 때의 지향도가 얼마나 감소했는지를 비교하기 위해 지향도 감소량을 dB값으로 나타내었다.
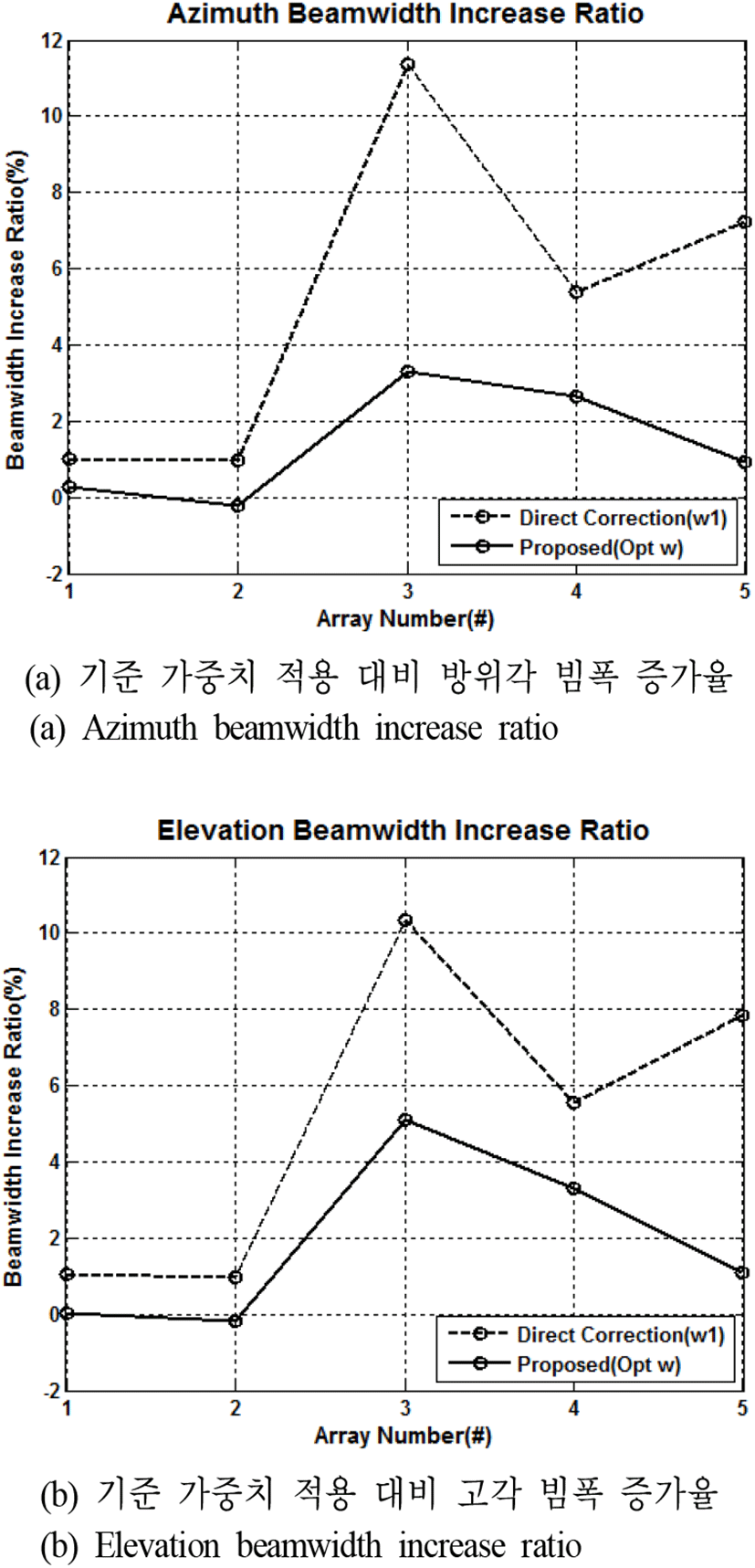
먼저, 그림 4에서 보면 5가지 종류의 모든 배열에 있어 본 논문에서 제시한 최적화 가중치 Opt w를 적용했을 때 빔폭 증가율이 작음을 알 수 있다. 동일한 부엽 수준을 나타내면서도 가능한 작은 빔폭을 가지는 것은 안테나 이득 측면에서 유리하고, 레이다 시스템에서 각도 정확도나 분해능 측면에서 조금 더 좋은 조건을 제공하므로, 위의 결과는 의미가 있다고 할 수 있다.
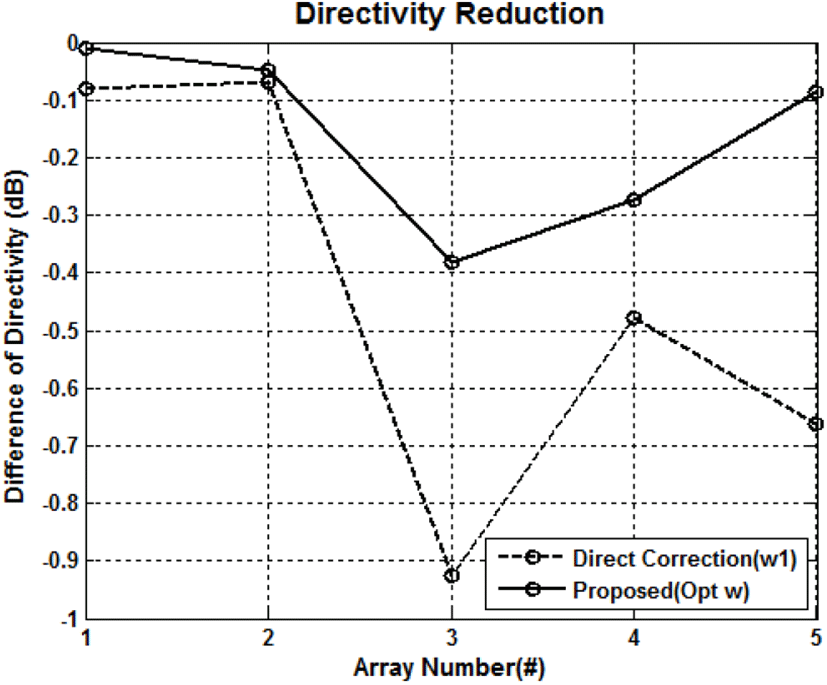
그림 5의 지향도 감소량은 안테나 이득에 직접적으로 관련되어 있으므로, 안테나 이득 측면에서 실제로 얼마나 유리한 지를 정량적으로 파악하기 위해 제시하였다. 그림 5에서 보면, 가중치 w1과 Opt w를 적용했을 때 두 경우 모두, 기준 가중치 w0를 적용한 것보다는 지향도가 감소함을 알 수 있는데, 이것은 당연한 결과로 부엽 수준을 낮추면서 그림 4의 결과와 같이 빔폭이 약간 넓어졌기 때문이다. 하지만, 그림 5에서 보듯이 원하는 부엽수준을 달성하기 위해 가중치의 테이퍼량을 직접 수정한 w1을 적용한 경우보다, 본 논문에서 제시한 방법을 통해 최적화 된 가중치 Opt w를 적용한 경우에 지향도 감소량이 더 적은 것을 확인할 수 있다. 물론, 목표로 하는 부엽수준이 −28 dB, −23 dB로 상대적으로 높고, 배열 형태가 정형화된 직사각형이나 원형(타원형 포함)에서 크게 벗어나지 않는 배열#1, 배열#2에서는, 지향도 감소량의 차이가 0.1 dB 이내의 무시할 수도 있는 정도이지만, 원하는 부엽 수준이 −35 dB로 더 낮고, 배열 형태가 정형화된 형태에서 꽤 벗어난 경우에는 0.5 dB 이상의 지향도 감소량에 대한 개선 효과가 있음을 확인할 수 있다.
그림 6에서는 지향도 감소량에 대한 차이가 0.5 dB 이상 차이나는 배열#3에 대해서, 기준가중치 및 최적화된 진폭 가중치의 배열면 분포를 나타내었다.
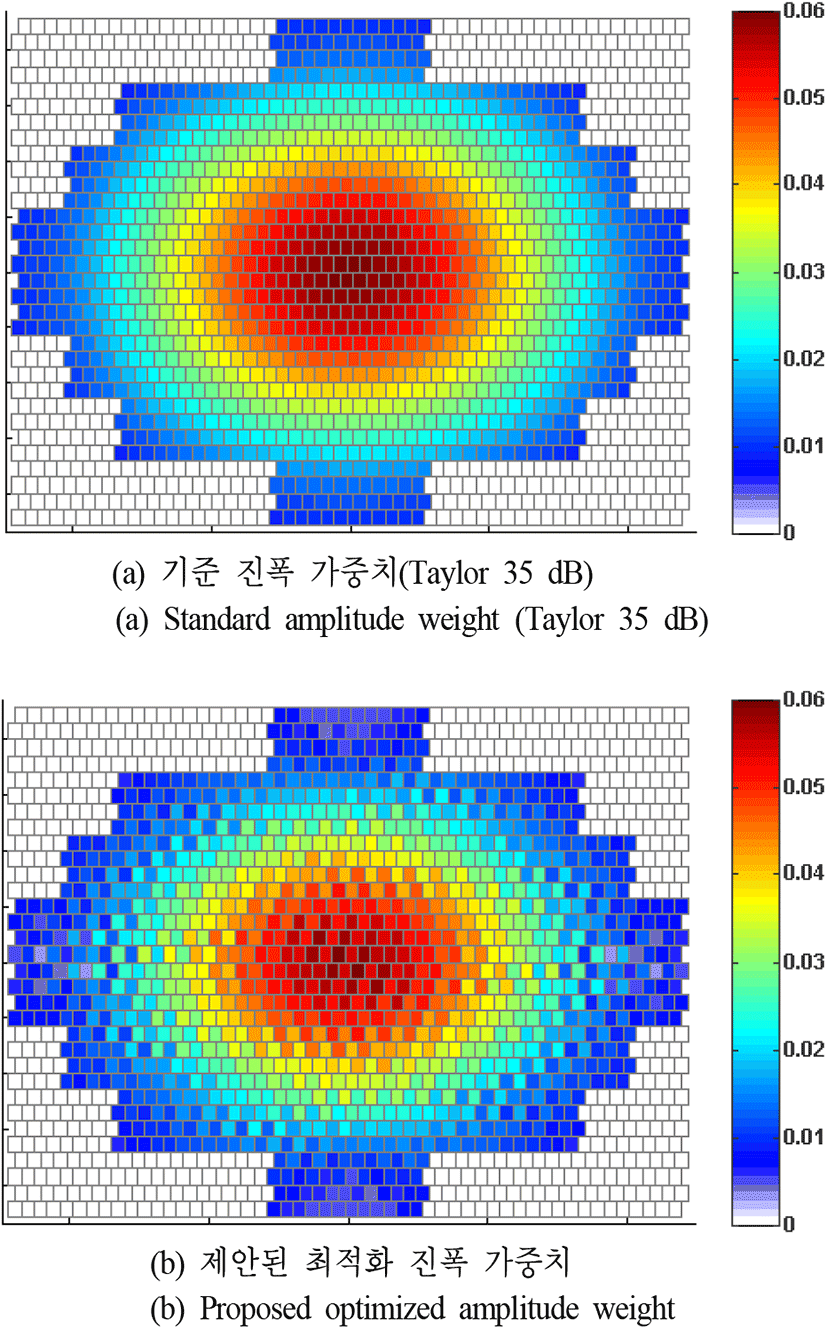
그림 6에서 보면 최적화된 진폭 가중치의 전체적인 경향은 기준 진폭 가중치를 따라서 형성되고 있지만, 소자별로 미세하게 크기가 조절되었음을 알 수 있다. 서론에서 언급하였듯이, 일반적인 능동위상배열에서 위와 같이 진폭 분포를 변화시키는 것은 수신빔에 대해서만 적용하며, 예전의 아날로그 방식의 능동위상배열의 경우에는 TRM의 감쇄기를 통해 위와 같은 진폭 분포를 구현할 수 있고, 최근의 디지털 레이다에서는 감쇄기의 양자화 오차(quantization error) 등 여러 가지 오차 요인 없이 더욱 유용하게 적용할 수 있다.
Ⅳ. 결 론
본 논문에서는 시스템의 종합적 요구사항을 고려하여 선정된 대칭성을 지닌 임의 형상 배열에 대해, 안테나 주빔 영역 이외의 전 공간에서 원하는 부엽 수준을 제공하는 최적의 진폭 가중치를 얻어 내는 방법을 제시하였다.
목표로 하는 부엽 수준을 구현하기 위해, 기준 진폭 가중치에 과도한 테이퍼를 제공하는 진폭 가중치에 비해, 본 논문에서 제시한 최적화된 진폭 가중치를 적용했을 때, 동일한 부엽 수준을 구현하면서도, 기준 진폭 가중치 적용 경우 대비한 빔폭 증가량 및 이에 따른 지향도 감소량을 상대적으로 작게 할 수 있음을 확인하였다.
본 논문에서 제안한 방법으로 얻어진 최적화된 진폭 가중치는, 전통적인 능동위상배열에서 사용되는 TRM 내부 감쇄기의 양자화 오차(quantization error) 등 여러 가지 오차 요인이 없는 최근의 디지털 레이다에서 더욱 유용하게 사용할 수 있을 것으로 판단된다.





