The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2020; 31(11):973-981

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2020.31.11.973

논문/REGULAR PAPERS

차량 탑재 바이스태틱 MIMO 레이다 시스템에서 도플러 전처리 기반 파라미터 추정 기법

이훈민¹

, 양훈기¹^,^*

Doppler-Preprocessing-Based Parameter Estimation in Automotive Bistatic MIMO Radar

Hun-Min Lee¹

, Hoon-Gee Yang¹^,^*

¹광운대학교 전자융합공학과

¹Department of Electronic Convergence Engineering, Kwangwoon University

^*Corresponding Author: Hoon-Gee Yang (e-mail: hgyang@kw.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 06, 2020; Revised: Sep 11, 2020; Accepted: Oct 21, 2020

Published Online: Nov 30, 2020

요약

도로환경에서 클러터에 의한 다중 경로 성분은 표적 차량의 DOD(direction of departure), DOA(direction of arrival) 및 도플러 주파수 추정오차를 유발한다. 본 논문에서는 다중 객체 환경에서 파라미터 추정 계산량을 줄이면서 페어링 문제를 해결할 수 있는 두 가지 ESPRIT 기반 바이스태틱 MIMO 레이다 알고리즘을 제안한다. 첫 번째로, 객체 부공간 알고리즘에서는 수신 신호로부터 객체 단위의 고유벡터를 추출해 프로세싱하는 것으로, 페어링 문제를 해결하지만 성능 열화가 발생함을 보인다. 두 번째, 도플러 전처리 알고리즘은 객체를 주파수 도메인에서 먼저 분리한 후 ESPRIT 알고리즘 및 필요시 객체 부공간 알고리즘을 추가 적용하는 방법으로, 제시한 방법이 페어링 문제뿐 아니라, 추정 오차를 줄일 수 있음을 보인다. 다중 객체, 다중 경로 환경을 시뮬레이션하여 두 제안 알고리즘의 (DOD, DOA, 도플러 주파수) 파라미터 추정 성능을 보인다.

Abstract

In a road environment, the clutter-induced multipath components cause errors in the estimations of the direction of departure (DOD), direction of arrival (DOA), and Doppler frequencies of nearby target vehicles. In this paper, two ESPRIT-based bistatic MIMO radar algorithms are proposed to solve the pairing problem while reducing the computational complexity in a multiobject environment. The first method, named the object subspace algorithm, solves the pairing problem by extracting and processing each object return on an eigenvector basis, but it is shown to exhibit performance degradation. In the second method, named the Doppler preprocessing algorithm, the object return is first separated in the frequency domain and the ESPRIT algorithm is then applied or the object subspace algorithm is reused, if necessary. Finally, the multiobject, multipath environment is simulated to show the parameter estimation (DOD, DOA, Doppler frequency) performances of the two proposed algorithms.

Keywords: Automotive Radar; MIMO; Bistatic; ESPRIT; DOA

Ⅰ. 서 론

차량용 레이다는 카메라, 라이다(Lidar), 초음파 센서 등과 더불어 첨단 운전자 보조 시스템(ADAS, advanced driver assistance systems) 및 자율주행 시스템에서 중추적인 역할을 하는 센서로, 주변 환경(기상조건, 도로환경 등)에 상관없이 차량, 보행자, 장애물 등의 객체를 탐지 할 수 있다는 장점이 존재해 적극적으로 활용되고 있다^[1].기존의 차량용 FMCW(frequency modulated continuous wave) 레이다는 거리와 속도만을 탐지해낼 수 있지만, 최근 들어서는 도심지 자율주행을 위해 도로 클러터들을 억제하면서 이동차량들에 대한 파라미터를 추출할 수 있는 단계로 발전하고 있다.

차량용 레이다 환경에서 객체탐지, 객체추적 및 자율주행을 위해 각각의 객체가 갖는 파라미터의 추출은 필수적이다. 차량용 레이다를 활용하여 추출 가능한 파라미터로는 DOD, DOA, 도플러 주파수 등이 있다. 만약 한 객체에서 추정한 DOD와 DOA가 같으면 표적, 서로 다르면 다중 경로 클러터라고 인지할 수 있으며, 각도 해상도를 높이기 위해 MIMO 레이다가 차량에 적용되고 있다^[1]. 특히 collocated MIMO 방식을 사용하면 개구면 크기를 작게 설계할 수 있어 차량 레이다 환경에 적합하며, virtual array를 형성해 각도 해상도를 향상시킬 수 있다는 장점이 있다^[2]. MIMO 레이다 환경에서는 각각의 수신 신호가 직교(orthogonal)해야 하므로, 파형 설계 및 최적화에 대한 연구 결과도 발표되었다.

객체 파라미터 추출 과정에서 오류를 일으키는 주요 원인 중 하나는 클러터이다. 특히 도로면이나 가로등과 같은 strong reflector 등이 다중 경로(multipath) 클러터 생성을 야기하며, 이를 억제하기 위해서 CFAR(constant false alarm rate) 알고리즘과 STAP(space time adaptive processing) 알고리즘 등이 적용되고 있다. CFAR 알고리즘으로는 CA-CFAR 외에도 OS-CFAR, Clutter map-CFAR 등이 적용되고 있다. STAP 알고리즘은 클러터를 억제하면서 이동표적을 탐지하는 적응필터 설계기술이 핵심이나, 도로환경에서는 직접 경로(direct path) 외에 다중 경로가 혼재되어 있으므로 MIMO 기술과 융합해 (DOD, DOA, 도플러 주파수)로 구성된 3차원 도메인에서 다중 경로 클러터를 효과적으로 억제하는 MIMO-STAP 기술로 발전하고 있다^[3].

MIMO-STAP을 적용하기 위해서는 매우 많은 양의 training data를 요구해 도로환경에서의 실시간 처리가 어려워 training 데이터를 줄이면서 STAP 알고리즘을 적용할 수 있는 partially adaptive MIMO-STAP 기법이 제안되었다^[4]. 이 논문에서는 strong reflector 성분 억제에 주안점을 두어 MIMO MVDR(minimum variance distortionless response) beamforming을 적용하여 DOD와 DOA가 같은 객체 성분만을 먼저 추출한 후, STAP 알고리즘을 적용하였다.

객체의 도플러 정보는 무시하고 bistatic MIMO 환경을 적용해서 DOD, DOA에 의한 위치정보를 찾으려는 연구 결과도 많이 발표되었다^[5]. 이들 방법들은 (DOD, DOA) 2차원 도메인에서 두 파라미터의 동시 추정에 목표를 두어 계산량 부담이 매우 큰 단점이 있다. 참고문헌 [6]에서는 ESPRIT 알고리즘을 사용하여 2개의 1차원 도메인에서 객체의 DOD와 DOA 정보를 추정함으로써 계산량을 획기적으로 줄였다. 두 개의 1차원 도메인 처리를 하는 경우 (DOD, DOA) 페어링 문제가 발생하며, 참고문헌 [7]에서는 matrix 변환을 이용해 페어링을 용이하게 하는 방법을 제안하였다. 위에서 언급한 대부분의 논문들은 모두 도플러 정보를 사용하지 않고 DOD, DOA를 추출하는 방법에 관한 내용이다.

본 논문에서는 DOD, DOA 파라미터 추정 알고리즘 제안 및 성능 개선을 위해 객체 도플러 정보를 적극 활용한 파라미터 추정을 하였다. 이를 위해 ESPRIT 알고리즘을 사용하고, 페어링 문제도 해결하면서 도플러 정보도 찾을 수 있는 두 가지 방법을 제안한다.

2장에서는 차량탑재 바이스태틱 MIMO 레이다 시스템을 모델링한 후, 제안 알고리즘 설명을 위해 기존 ESPRIT 알고리즘 연산 과정을 설명한다. 3장에서는 기존 알고리즘의 한계점을 보완하기 위한 객체 부공간 알고리즘을 소개한다. 또한 객체 부공간 알고리즘의 성능열화 요인을 간단한 예제를 통해 확인하고, 성능 열화를 보완한 도플러 전처리 알고리즘을 제시한다. 4장에서는 표적과 다중 경로 클러터가 존재하는 도로 환경에서의 시뮬레이션을 통해서 두 가지 제안 알고리즘의 성능을 보인다.

Ⅱ. 바이스태틱 MIMO 레이다 시스템 모델링 및 ESPRIT 각도추정 알고리즘

2-1 바이스태틱 MIMO 레이다 시스템 모델링

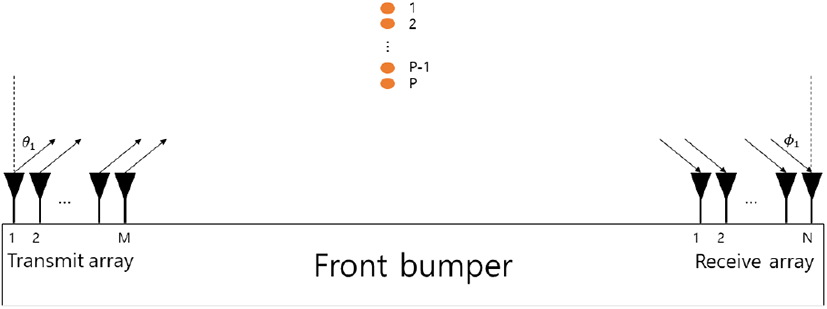
그림 1은 본 논문에서 고려하고 있는 차량탑재 바이스태틱 MIMO 레이다 시스템이다. 송신 안테나는 M개이며 각각의 안테나에서 전송되는 신호는 서로 직교한다. 수신 안테나는 N개로 각 안테나 수신부에는 M개의 정합필터를 이용해서 각 송신 안테나 신호를 분리시킬 수 있다. 객체 개수는 P개이며, p(p=1, … , P)번째 객체에 대한 DOD는 θ_p, DOA는 ϕ_p라 하자. 이 때 θ_p = ϕ_p이면 p번째 객체는 표적이고, θ_p ≠ ϕ_p이면 p번째 객체는 다중 경로 클러터에 의한 성분이다. 안테나와 객체 간에는 far-field 조건을 만족하며 안테나 간 간격은 캐리어 주파수의 반파장(d=λ/2)이다.

그림 1. | Fig. 1. 차량 탑재 바이스태틱 MIMO 레이다 모델 | Vehicle-mounted bistatic MIMO radar model.

Download Original Figure

p번째 객체에 대한 송신 안테나 조향벡터 a(θ_p)는 다음과 같이 나타낼 수 있다.

a (θ p) = [1, e − j 2 π f c d sin ϕ p c, …, e − j 2 π f c (M − 1) d sin θ p c] T

(1)

f_c는 캐리어 주파수, d는 안테나 간 간격, c는 전파 속도이다. p번째 객체에 대한 수신 안테나 조향벡터 b(ϕ_p)는 다음과 같이 나타낼 수 있다.

b (ϕ p) = [1, e − j 2 π f c d sin θ p c, …, e − j 2 π f c (N − 1) d sin ϕ p c] T

(2)

이때 p번째 객체의 (DOD, DOA) 조향 행렬 A는 다음과 같이 나타낼 수 있다.

A = [b (ϕ 1) ⊗ a (θ 1), b (ϕ 2) ⊗ a (θ 2), …, b (ϕ P) ⊗ a (θ P)]

(3)

⊗는 크로네커곱을 나타내고, A 크기는 MN×P이다.

하나의 송신 안테나에서 방사되어 하나의 수신 안테나에 수신된 시간축 수신 신호 벡터 S(t)는 다음과 같다.

S (t) = [s 1 (t), s 2 (t), …, s p (t), …, s p (t)] T

(4)

여기서 p번째 성분 s_p(t)는 다음과 같다.

s p (t) = η p e j 2 π f p t e − j 2 π (R p + α) λ

(5)

η_p는 반사계수, f_p는 바이스태틱 도플러 주파수를 나타낸다. R_p는 레이다 플랫폼과 p번째 객체의 초기 왕복 거리, α는 각 스냅샷(snapshot)마다 레이다와 표적간의 거리가 비선형적으로 변하는 것을 반영한 residual 랜덤 거리로, α≪νT (ν=플랫폼 속도, T=RPI)이다.

바이스태틱 레이다 환경에서 p번째 객체에 의한 도플러 주파수는 다음과 같다.

f D, p = 1 λ (v p − v v e h i c l e) ⋅ i t x, p + 1 λ (v p − v v e h i c l e) ⋅ i r x, p

(6)

v_p는 p번째 객체의 속도, v_vehicle은 자기차량의 속도를 나타내며, i_tx,p는 송신 배열안테나와 p번째 객체가 이루는 방향벡터, i_rx,p는 수신 배열안테나와 p번째 객체가 이루는 방향벡터를 나타낸다.

수신단 정합필터를 통과한 수신 배열안테나 수신 신호 벡터Y(t)는 다음과 같이 나타낼 수 있다.

Y (t) = A S (t) + N (t)

(7)

Y(t)의 크기는 MN×1이며, N(t)는 평균이 0이고, 공분산 행렬은 σ²I인 복소 백색 가우시안 잡음(complex AWGN)이다.

2-2 ESPRIT 각도 추정 알고리즘

본 절에서는 다음 장에서 제안하는 알고리즘 설명을 위해 필요한 기존 ESPRIT 알고리즘을 요약하였다^[6],[8]. 수신 신호의 공분산 행렬 R은 R = E[Y(t)Y(t)^H]이며, []^H는 켤레전치(Hermitian)를 의미한다. 공분산 행렬을 고유값 분해하여 신호 부공간과 잡음 부공간으로 나누면 다음과 같다.

R = U Λ U H = U s Λ s U s H + U n Λ n U n H

(8)

이때 U_s는 MN×P 행렬로 신호의 고유벡터이고, U_n은 잡음의 고유벡터를 나타낸다. U_s 행렬의 부분 행렬은 다음과 같다.

U t 1 = I N ⊗ [I M − 1 0] U s

(9)

U t 2 = I N ⊗ [I M − 1] U s

(10)

이때 I_N과 I_M−1은 각각 N차, M−1차 단위행렬을 의미한다. 식 (9)와 식 (10)에서 ‘0’은 길이가 M−1이고, 각각의 성분이 모두 0인 열벡터이다.

송신 안테나에 대한 신호 부공간 rotating operator ψ_t는 다음과 같이 쓸 수 있다.

ψ t = (U t 1 H U t 1) − 1 U t 1 H U t 2

(11)

ψ_t의 고유값 diag {ν₁, ν₂, …, ν_P}을 이용해 spatial frequency μ_p를 찾으면 DOD를 추정할 수 있으며, 아래의 관계식을 이용한다.

μ p = arg (v p), θ p = arcsin (− λ 2 π d μ p)

(12)

DOA 또한 식 (9)～식 (12)의 방법을 적용하여 추정할 수 있다.

ESPRIT 알고리즘을 활용한 각도추정 방법은 송신 신호와 수신 신호 벡터를 독립적으로 처리하므로 고유값 크기순으로 정렬해 객체의 (DOD, DOA) 페어링을 하는 경우 페어링 오류가 발생할 수 있다^[9],[10]. 다음 장에서는 페어링 오류를 해결하는 객체 부공간 알고리즘과 객체 부공간 알고리즘의 성능을 개선할 수 있는 도플러 전처리 알고리즘을 제시한다.

Ⅲ. 제안 알고리즘

3-1 객체 부공간 알고리즘

식 (8)의 U_s 행렬은 다음과 같이 객체 고유벡터들의 집합으로 나타낼 수 있다.

U s = [U s, 1, U s, 2, …, U s, p, …, U s, p]

(13)

U_s,p는 p번째 객체를 나타내는 MN×1 크기의 고유벡터이다. 첫 번째 객체의 고유벡터 U_s,1으로부터 다음과 같이 부분행렬U_t1,1, U_t2,1 을 만들 수 있다.

U t 1, 1 = I N ⊗ [I M − 1 0] U s, 1

(14)

U t 2, 1 = I N ⊗ [I M − 1] U s, 1

(15)

두 부분행렬을 이용해 송신 안테나에 대한 신호 부공간 rotating operator ψ_t,1는 다음과 같이 구할 수 있다.

ψ t, 1 = (U t 1, 1 H U t 1, 1) − 1 U t 1, 1 H U t 2, 1

(16)

식 (16)의 ψ_t,1는 첫 번째 객체의 신호 부공간 rotating operator 만을 나타내며, ψ_t,1의 고유값 diag {ν₁}을 이용해 공간 주파수 μ₁을 찾은 뒤 식 (12)에 대입하면 첫 번째 객체에 대한 DOD를 추정할 수 있다.

첫 번째 객체가 갖는 DOA의 추정을 위해서 U_s,1으로부터 다음과 같이 두 부분행렬을 구할 수 있다.

U r 1, 1 = [I N − 1 0] ⊗ I M U s, 1

(17)

U r 2, 1 = [I N − 1] ⊗ I M U s, 1

(18)

U_r1,1, U_r2,1을 이용해 ψ_r,1을 찾을 수 있으며, 위와 같은 과정을 통해 DOA도 추정할 수 있다.

각각의 객체 고유벡터들을 식 (13)～식 (18)에 따라 순차적으로 처리하여 P개의 (DOD, DOA) 순서쌍을 얻을 수 있다. 객체 부공간 프로세싱 알고리즘에 입력되는 고유벡터는 1개 객체에 대한 값이므로 각도 추정결과인 (DOD, DOA) 순서쌍은 1개 객체에 대한 값만 존재해, 페어링 오류는 발생하지 않는다.

모든 객체의 (DOD, DOA) 순서쌍을 추정한 후에는 A 행렬의 추정값 $A ˜$ 를 얻을 수 있으며, 따라서 Y(t)는 다음과 같이 근사화할 수 있다.

Y (t) = A ˜ S (t)

(19)

그러므로 S(t)의 추정값 $S ˜ (t)$ 는 다음과 같이 구할 수 있다.

S ¯ (t) ≃ A ¯ † Y (t)

(20)

여기서 $A ˜ †$ 는 $A ˜$ 의 의사 역행렬(pseudo-inverse) 이다. 추정한 $S ˜ (t)$ 를 퓨리에 변환하면 각각의 객체가 갖는 도플러 주파수를 얻어낼 수 있다.

객체 부공간 알고리즘을 적용하는 경우, (DOD, DOA) 순서쌍 추정값을 얻는 과정에서 오차 요인이 존재하며, 이에 대해서 다음의 예시를 통해 설명한다. N=2, M=3, P=2이며, 잡음이 없는 경우, t=T 에서의 수신 신호는 식 (21)과 같이 표현할 수 있다.

Y (t) | t = T = Y (T) = A S (T) = [η 1 e j 2 π f 1 T + η 2 e j 2 π f 2 T η 1 e j 2 π f 1 T e − j 2 π f c d sin θ 1 c + η 2 e j 2 π f 2 T e − j 2 π f c d sin θ 2 c η 1 e j 2 π f 1 T e − j 2 π f c 2 d sin θ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c 2 d sin θ 2 c η 1 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c d sin ϕ 2 c η 1 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c e − j 2 π f c d sin θ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c d sin ϕ 2 c e − j 2 π f c d sin θ 2 c η 1 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c e − j 2 π f c 2 d sin θ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c e − j 2 π f c 2 d sin θ 1 c] = [a b c d e f]

(21)

편의상 각각의 벡터성분을 알파벳으로 단순화 하여 나타내었으며, 이때 공분산 행렬은 아래와 같다.

R = Y (T) Y H (T) = [a a ¯ a b ¯ a c ¯ a d ¯ a e ¯ a f ¯ b a ¯ b b ¯ b c ¯ b d ¯ b e ¯ b f ¯ c a ¯ c d ¯ c c ¯ c d ¯ c e ¯ c f ¯ d a ¯ d b ¯ d c ¯ d d ¯ d e ¯ d f ¯ e a ¯ e b ¯ e c ¯ e d ¯ e e ¯ e f ¯ f a ¯ f b ¯ f c ¯ f d ¯ f e ¯ f f ¯]

(22)

$[¯]$ 연산자는 켤레복소수를 나타낸다. 식 (22)에서 대각성분(diagonal term) 및 비대각성분(off-diagonal term)을 각각 하나씩 샘플로 추출해서 값을 조사해 보자.

식 (22)에서 (5,4)에 위치한 비대각성분 $e d ¯$ 는 식 (23)과 같이 표현된다. 또한 식 (22)에서 (5, 5)에 위치한 대각성분 $e e ¯$ 값은 식 (24)와 같다.

식 (23), 식 (24)의 도플러 주파수 성분을 보면 f₁, f₂ 외에 각 도플러 주파수 값의 선형 조합(linear combination)인 새로운 도플러 주파수(f₂−f₁)가 발생하며, 객체 개수가 많아지면 무수히 복잡한 조합값을 갖는 새로운 도플러 주파수가 생성된다. 새로이 생성된 도플러 주파수 f₂−f₁은 고유값 분해를 하여도 f₁과 f₂로 각각 분리할 수 없으며, 잡음으로 작용한다. 즉, 각 객체의 고유벡터 U_s,p에서 자신의 도플러 주파수 외에 다른 도플러 주파수가 생성된다. 이는 (DOD, DOA) 추정 시 오차 증가 요인이 되며, 추가적으로 객체 도플러 주파수 추정 오차를 증가시킬 수 있다.

e d ¯ = {η 1 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c e − j 2 π f c d sin θ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c d sin ϕ 2 c e − j 2 π f c d sin θ 2 c} = η 12 e − j 2 π f c d sin θ 1 c + η 22 e − j 2 π f c d sin θ 1 c + η 1 η 2 e j 2 π (f 2 − f 1) T e − j 2 π f c d (sin θ 1 − sin ϕ 1 c) e − j 2 π f c d sin θ 2 c

(23)

e e ¯ = {η 1 e j 2 π f 1 T e − j 2 π f c d sin ϕ 1 c e − j 2 π f c d sin θ 1 c + η 2 e j 2 π f 1 T e − j 2 π f c d sin ϕ 2 c e − j 2 π f c d sin θ 2 c} = η 12 e − j 2 π f c d sin θ 1 c + η 22 e − j 2 π f c d sin θ 1 c + η 1 η 2 e j 2 π (f 2 − f 1) T e − j 2 π f c d (sin θ 1 − sin ϕ 1 c) e − j 2 π f c d sin θ 2 c

(24)

3-2 도플러 전처리 알고리즘

t=nT(n=0,1,…,snapshot number)인 순간 수신 배열안테나에서는 정합필터를 통해 송신 신호별 표적 산란 신호를 구분해서 Y(nT) 를 얻을 수 있다. MN×1 크기를 갖는 Y(nT) 의 성분 y_i,j(nT) 는 i번째 송신 안테나에 서 송신된 후 j번째 수신 안테나에 수신된 신호이다. Y(nT) 의 모든 성분에 대해 FFT(fast Fourier transform)를 이용해 파워 스펙트럼(PSD)을 얻을 수 있으며, 이들을 인코히어런트하게 더해서 객체에 대한 도플러 피크들을 검출할 수 있다. 즉, $∑ i, j | F F T [y i, j (t)] |$ 을 연산한 후 주파수 도메인에서 CFAR 알고리즘을 적용해 각 객체들의 도플러 주파수를 추정할 수 있다. 도플러 주파수를 추정한 후에는 각 주파수 성분을 추출할 수 있는 FIR 필터들을 설계한다. 이때 필터의 탭 간격(τ)을 충분히 작게 하여 $1 2 τ ≥ f D i$ 를 만족해야 하며, 탭의 개수에 따라 주파수 해상도가 결정된다. 예를 들어 W_D1[nT]가 도플러 주파수 f_D1을 추출하는 필터라 하자. Y(nT) 의 모든 성분 {y_i,j(nT)}에 대해 W_D1[nT]을 통과시키면 MN×1 크기를 갖는 {z_i,j(nT)}을 얻을 수 있다. 이때 {z_i,j(nT)}에 ESPRIT 알고리즘을 적용하면 도플러 주파수 f_D1을 갖는 객체에 대한 (DOD, DOA)를 추정할 수 있다.

ESPRIT 알고리즘의 수신 신호 공분산 행렬에서 dominant한 고유값이 두 개 이상 나오는 경우는 우연히 두 개 이상의 객체가 유사한 바이스태틱 도플러 주파수를 가진 것이므로, 3.1 절에서 설명한 객체 부공간 알고리즘을 적용해 각 객체에 대한 (DOD, DOA)를 분리하여 추정할 수 있다. 각 객체에 대한 (DOD, DOA)를 획득한 후에는 3.1 절의 식 (19), 식 (20)을 이용해 각 객체의 도플러 주파수를 찾을 수 있다.

이상의 내용을 정리하면 아래의 과정으로 나타낼 수 있다.

Step 1. $∑ i, j | F F T [y i, j (t)] |$ 에 의한 수신 신호의 PSD 계산

Step 2. PSD로 부터 CFAR 알고리즘에 의한 각 객체의 도플러 주파수 f_D추정

Step 3. f_D를 이용한 FIR 필터W_Dp[nT] 설계

Step 4. 필터 출력 {z_i,j(nT)}를 ESPRIT 알고리즘에 적용

Step 4-1. {z_i,j(nT)}의 공분산 행렬에서 dominant 고유 값이 1개 나오는 경우→ (DOD, DOA) 추정

Step 4-2. 공분산 행렬에서 dominant 고유값이 2개 이상나오는 경우→ 객체 부공간 알고리즘에 대입해 (DOD, DOA) 추정

Step 5. 추정 (DOD, DOA)를 이용한 의사역행렬 $A ˜ †$ 추정 및 객체 도플러 주파수 계산

Ⅳ. 시뮬레이션

표 1은 시뮬레이션에 사용된 차량 MIMO 레이다 파라미터이다. PRI가 0.1 m/sec이고, 펄스개수는 100개이므로, CPI 동안의 시간은 10 m/sec이다.

표 1. | Table 1. 시뮬레이션 파라미터 | Simulation parameter.

Parameter	Value
Carrier frequency	77 GHz
Number of TX antennas (M)	20
Number of RX antennas (N)	20
SNR	10 (dB)
Number of pulse	100
PRF	10 kHz
Ego velocity	18 m/s

Download Excel Table

그림 2는 표적과 다중 경로 클러터가 혼재하는 도로환경을 나타낸 것으로, 표적과 다중 경로 클러터 성분이 각각 3개씩 존재하도록 모델링하였다. 표적과는 달리 클러터 수신 신호 성분은 다중 경로에 의해 전파가 굴절되므로 DOD와 DOA가 다른 값을 가진다. 클러터 1, 2는 각각 표적 1, 2와 DOA가 같으며, 클러터 3은 표적 3과 DOD가 같도록 모델링하였다. 즉, 클러터 1과 클러터 2에 반사되어 수신된 신호는 송신 신호가 클러터에 의해 먼저 반사된 뒤 표적에 반사되어 돌아오는 것을 의미하며, 클러터 3에 의해 발생하는 수신 신호는 송신 신호가 표적에 먼저 반사된 뒤 클러터에 반사되어 돌아오는 것을 의미한다. 수신 신호 모델링을 위해 필요한 객체 파라미터는 아래의 표 2와 같이 요약할 수 있으며, 알고리즘 성능평가를 위해 의도적으로 표적과 클러터가 DOD나 DOA 중 한 값이 같도록 하였다.

그림 2. | Fig. 2. 표적과 다중 경로 클러터가 존재하는 도로환경 | Road environment with target and multipath clutter.

Download Original Figure

표 2. | Table 2. 객체 파라미터 | Object parameter.

	DOD	DOA	Reflection coefficient	Doppler frequency
Target 1	20°	20°	0.75	−482 Hz
Clutter 1	27°	20°	0.1	−4.36 kHz
Targer 2	5°	5°	0.7	1.53 kHz
Clutter 2	10°	5°	0.12	−3.78 kHz
Target 3	0°	0°	0.78	−385 Hz
Clutter 3	0°	8°	0.08	−4.81 kHz

Download Excel Table

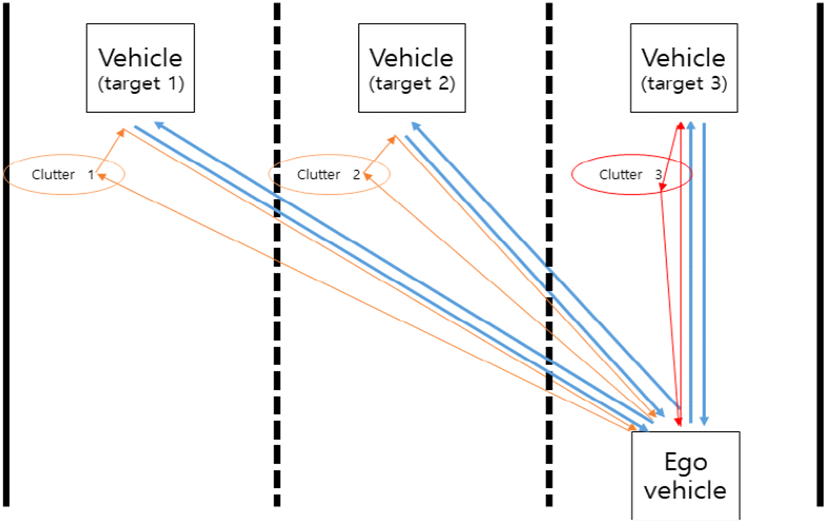
표 2에서, 차량 플랫폼이 바라보는 방향, 즉, 도로 진행방향을 0°로 기준하여 각 객체의 각도 (DOD, DOA)를 설정하였다. 클러터의 복소 반사계수는 다중 경로 환경에서 많은 감쇠가 일어나는 것을 고려해 표적의 반사계수에 비해 크기가 작게 모델링하였다. 또한 두 객체(표적 1, 표적 3)의 바이스태틱 도플러 주파수가 유사해지는 경우를 고려하기 위해 표적 1과 표적 3의 도플러 주파수 차이를 97 Hz로 설정하였으며, 이는 3.2 절에서 제시한 FIR 필터의 대역폭보다 작은 값이라고 가정하였다.

그림 3은 객체 부공간 프로세싱 알고리즘과 도플러 전처리 알고리즘에서의 PSD를 나타낸다. 두 가지 제안 알고리즘 모두에서 식 (19), 식 (20)을 활용해 도플러 주파수를 추정하였으며, 결과값은 표 3에서 확인할 수 있다.

그림 3. | Fig. 3. 각 객체의 도플러 주파수 추정 결과 | Doppler frequency estimation result of each object.

Download Original Figure

표 3. | Table 3. 제안 알고리즘을 적용한 객체 파라미터 추정결과 | Object parameter estimation results using the proposed algorithms.

		DOD		DOA		Doppler frequency
		Mean	Variance	Mean	Variance	Mean	Variance
Result 1	Target 1	18.4°	8.56×10⁻²	18.4°	8.52×10⁻²	−482 Hz	0.194
	Clutter 1	26.4°	2.26×10⁻²	19.7°	9.87×10⁻³	−4.36 kHz	0.220
	Target 2	5.03°	2.51×10⁻³	5.02°	2.51×10⁻³	1.53 kHz	1.00×10⁻²
	Clutter 2	9.94°	7.02×10⁻³	5.17°	3.08×10⁻³	−3.78 kHz	0.242
	Target 3	1.51°	7.16×10⁻²	1.52°	7.22×10⁻²	−385 Hz	0
	Clutter 3	0.510°	1.75×10⁻²	8.16°	6.84×10⁻³	−4.81 kHz	0.222
Result 2	Target 1	19.7°	1.20×10⁻⁴	19.7°	1.56×10⁻⁴	−482 Hz	0.149
	Clutter 1	26.9°	4.46×10⁻³	19.9°	2.74×10⁻³	−4.36 kHz	0.122
	Target 2	5.00°	2.73×10⁻⁵	5.00°	3.80×10⁻⁵	1.53 kHz	0
	Clutter 2	10.0°	1.96×10⁻³	5.04°	1.84×10⁻³	−3.78 kHz	6.58×10⁻²
	Target 3	0.648°	2.02×10⁻⁴	0.649°	2.00×10⁻⁴	−385 Hz	0
	Clutter 3	0.268°	5.19×10⁻³	8.01°	7.14×10⁻³	−4.81 kHz	0.179

Download Excel Table

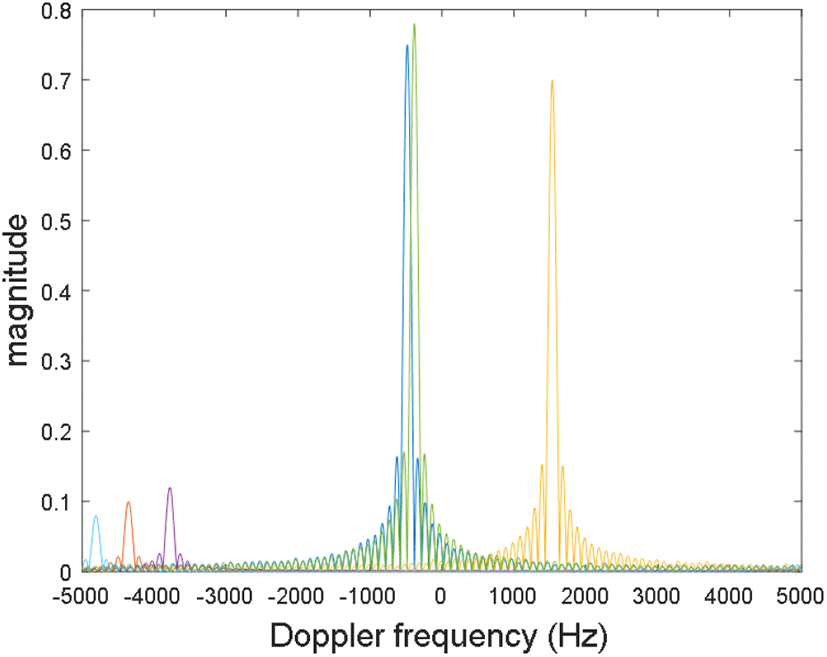
표 3은 제안 알고리즘 100회 시행에 대한 파라미터의 평균과 분산을 나타내며, 결과 1은 객체 부공간 알고리즘을, 결과 2는 도플러 전처리 알고리즘을 적용한 파라미터 추정 결과를 나타낸다. 결과 2에서의 각도정보 추정치 평균이 표 2의 값과 더 유사하며, 분산도 더 작았다. 추정한 (DOD, DOA)를 이용해서 $A ˜ †$ 을 구한 후 도플러 주파수를 추정했으며 도플러 주파수 값은 두 방법 모두 오차가 거의 없음을 확인할 수 있다. 표 4는 객체 파라미터 추정 결과에 대한 오차의 평균 및 오차항의 분산을 나타내며, 간단한 비교를 위해 표적에 대한 값만을 나타내었다. 결과 2에서의 평균과 분산 모두가 결과 1의 값들에 비해 더 작은 것을 확인할 수 있다.

표 4. | Table 4. 객체 파라미터 추정결과 오차의 평균과 오차항의 분산 | Mean of error and variance of error term about object parameter estimation results.

		DOD		DOA		Doppler frequency
		Mean	Variance	Mean	Variance	Mean	Variance
Result 1	Target 1	−1.63°	8.56×10⁻²	−1.63°	8.52×10⁻²	0.567 Hz	0.194
	Target 2	0.0263°	2.51×10⁻³	0.0224°	2.51×10⁻³	0.504 Hz	1.00×10⁻²
	Target 3	1.51°	7.16×10⁻²	1.52°	7.22×10⁻²	0.462 Hz	0
Result 2	Target 1	−0.311°	1.20×10⁻⁴	−0.310°	1.56×10⁻⁴	0.647 Hz	0.149
	Target 2	0.00373°	2.73×10⁻⁵	0.00381°	3.80×10⁻⁵	0.514 Hz	0
	Target 3	0.648°	2.02×10⁻⁴	0.649°	2.00×10⁻⁴	0.462 Hz	0

Download Excel Table

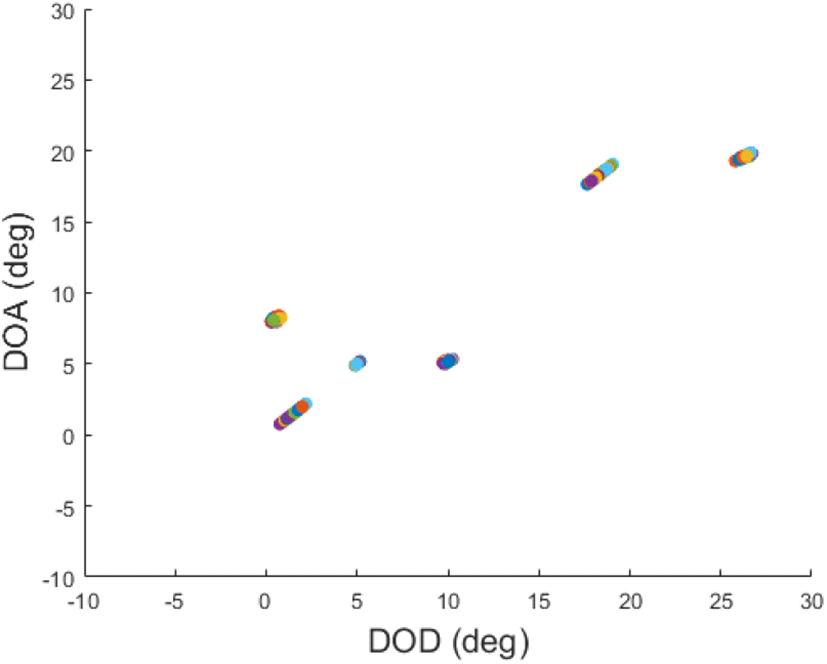
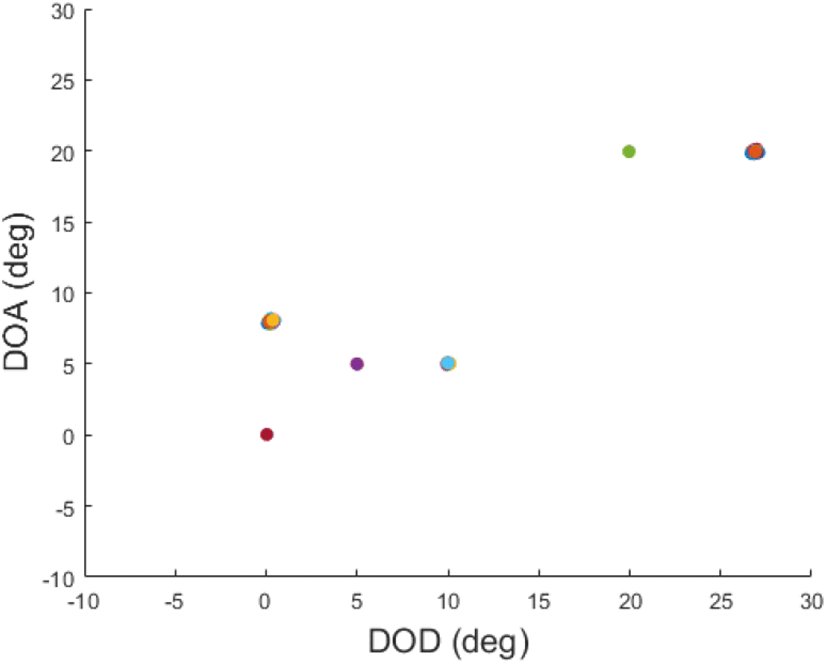
그림 4와 그림 5는 각각 표 3에서 결과 1, 결과 2의 (DOD, DOA) 추정 결과를 나타낸 것이다. 결과 2의 분산이 더 작은 것을 두 그림에서도 확인할 수 있다. 본 논문에서는 객체별 (DOD, DOA) 및 도플러 주파수 추정 알고리즘 및 추정 성능에 역점을 두었으나, 실제 시스템의 경우, 추정된 (DOD, DOA) 및 도플러 주파수 값은 이동 표적 및 strong reflector에 의한 클러터 분리, STAP 알고리즘 등에 의한 클러터 억제 등 후처리 과정에 활용될 것이다.

그림 4. | Fig. 4. 객체 부공간 알고리즘 (DOD, DOA) 추정 결과 | (DOD, DOA) estimation result from the object subspace algorithm.

Download Original Figure

그림 5. | Fig. 5. 도플러 전처리 알고리즘 (DOD, DOA) 추정 결과 | (DOD, DOA) estimation result from the Doppler preprocessing algorithm.

Download Original Figure

Ⅴ. 결 론

바이스태틱 MIMO 레이다 시스템에서 기존 ESPRIT 알고리즘은 작은 연산량을 요구해 차량 탑재 레이다 적용에 적합하나, 다중 객체 환경에서 페어링 문제를 야기한다. 본 논문에서는 페어링 문제 해결을 위해 기존 ESPRIT 알고리즘을 보완하는 두 가지 알고리즘을 제안하였다. 첫 번째로 제안한 객체 부공간 알고리즘은 페어링 문제는 해결되었으나, 고유벡터에 다른 객체의 도플러 주파수가 포함되어 추정 성능 열화가 발생함을 예시를 통해 분석하였다. 두 번째로 제안한 도플러 전처리 알고리즘에서는 주파수 도메인 전처리 과정에 의해 객체를 미리 분리하였으므로 페어링 문제 해결뿐 아니라, 추정 성능 열화를 줄일 수 있었으며, 객체들의 도플러 주파수가 유사한 경우에는 객체 부공간 알고리즘을 추가로 적용해 안정적인 파라미터 추정 결과를 얻을 수 있음을 보였다. 다중 객체 다중 경로 환경을 시뮬레이션하여 제안 알고리즘을 적용하였으며, 분석한 결과와 일치하는 추정 결과를 얻었다. 향후에는 본 논문에서 제안한 기법에 의해 추정한 파라미터를 객체추적 알고리즘에 적용하고자 한다.

References

[1].

S. M. Patole, M. Torlak, D. Wang, and M. Ali, “Automotive radars a review of signal processing techniques,” IEEE Signal Processing Magazine, vol. 34, no. 2, pp. 22-35, March. 2017.

[2].

S. Lutz, K. Baur, and T. Walter, “77 GHz lens-based multistatic MIMO radar with colocated antennas for automotive applications,” IEEE/MTT-S International Microwave Symposium Digest, Montreal, Canada, pp. 1-3, June. 2012.

[3].

G. Hickman, J. L. Krolik, “MIMO GMTI radar with multipath clutter suppression,” IEEE Sensor Array and Multichannel Signal Processing Workshop, Jerusalem, Israel, pp. 65-68, Oct. 2010.

[4].

J. Yu, J. Krolik, “MIMO multipath clutter mitigation for gmti automotive radar in urban environments,” IET International Conference on Radar Systems, Glasgow, UK, pp. 1-5, Oct. 2012.

[5].

H. Jiang, J. K. Zhang, and K. M. Wong, “Joint DOD and DOA estimation for bistatic MIMO radar in unknown correlated noise,” IEEE Transactions on Vehicular Technology, vol. 64, no. 11, pp. 5113-5125, Nov. 2015.

[6].

C. Duofang, C. Baixiao, and Q. Guodong, "Angle estimation using ESPRIT in MIMO radar,” ELECTRONICS LETTERS, vol. 44, no. 12, pp. 770-771, June. 2008.

[7].

C. Jinli, G. Hong, and S. Weimin, “Angle estimation using ESPRIT without pairing in MIMO radar,” Electronics Letters, vol. 44, no. 24, pp. 1422-1423, Nov. 2008.

[8].

Z. Chen, G. K. Gokeda, and Y. Yu, Introduction to Direction-of-Arrival Estimation, Artech house, pp. 81-92, 2010.

[9].

K. G. Yeo, Y. S. Chung, H. G. Yang, J. M. Kim, and W. Z. Chung, “Reduced-dimension DOD and DOA estimation through projection filtering in bistatic MIMO radar with jammer discrimination,” IET Radar, Sonar & Navigation, vol. 11, no. 8, pp. 1228-1234, Aug. 2017.

[10].

C. Yu, X. Zhang, Y. Bai, and Z. Du, “DOD-DOA estimation by exploiting signal cyclostationarity for bistatic MIMO radar,” IEEE International Conference on Signal Processing, Communication and Computing, KunMing, China, pp. 1-4, Aug. 2013.

Author Information

이 훈 민 [광운대학교/석사과정]

jkiees-31-11-973-i1

https://orcid.org/0000-0002-9747-5322
2019년 2월: 광운대학교 전자융합공학과 (공학사)
2019년 3월~현재: 광운대학교 전자융합공학과 석사과정
[주 관심분야] 무선통신 시스템, 레이다 신호처리, 객체 추적

양 훈 기 [광운대학교/교수]

jkiees-31-11-973-i2

https://orcid.org/0000-0001-8996-2561
1985년 2월: 연세대학교 전자공학과 (공학사)
1987년 5월: 미국 SUNY at Buffalo University 전기컴퓨터공학과 (공학석사)
1992년 4월: 미국 SUNY at Buffalo University 전기컴퓨터공학과 (공학박사)
1993년 3월～현재: 광운대학교 전자융합공학과 교수
[주 관심분야] 무선통신 시스템, UWB, RFID, 스펙트럼공학, 레이다 신호처리