The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2019; 30(7):573-582

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2019.30.7.573

논문/REGULAR PAPERS

기동하는 소형 무인기의 실측 데이터를 이용한 미세운동 특성 분석

강기봉^†

, 최인오

, 최재호

, 선선구^*

, 이정수^*

, 조병래^*

, 박상홍^**

, 김경태

Analysis of Micro-Motion Characteristics Caused by Maneuvering a Small Unmanned Aerial Vehicle Acquired from X-Band Radar

Ki-Bong Kang^†

, In-Oh Choi

, Jae-Ho Choi

, Sun-Gu Sun^*

, Jung-Soo Lee^*

, Byung-Lae Cho^*

, Sang-Hong Park^**

, Kyung-Tae Kim

포항공과대학교 전자공학과

^*국방과학연구소

^**부경대학교 전자공학과

Department of Electronic Engineering, Pohang University of Science and Technology

^*Agency of Defence Development

^**Department of Electronic Engineering, Pukyong National University

^†Corresponding Author: Ki-Bong Kang (e-mail: kkb131@postech.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 13, 2019; Revised: Mar 25, 2019; Accepted: Jul 01, 2019

Published Online: Jul 31, 2019

요약

소형 무인기 탐지 및 식별을 위해 미세운동 특성분석 연구가 활발하게 진행되고 있다. 하지만 소형무인기가 기동하는 경우 미세운동 성분뿐만 아니라, 병진운동 성분 역시 존재하며, 소형 무인기의 위치에 따라 레이다 관측각도가 변하게 된다. 이러한 병진운동 및 관측각도 성분은 미세운동 신호 특성에 영향을 준다. 따라서 각 성분들이 미세운동 신호 특성에 미치는 영향을 사전에 분석하는 연구가 수행되어야 한다. 본 논문에서는 실제 기동 환경을 고려하여 소형 무인기 신호 모델링을 수행하였으며, 미세운동 성분의 주파수 스펙트럼 및 스펙트로그램단 특성 분석을 수행하였다. 최종적으로 실측 데이터를 바탕으로 병진운동과 관측각도 성분이 미세운동 신호에 미치는 영향 분석을 성공적으로 수행하였다.

Abstract

Recently, feature analysis of micro-motion characteristics has been being actively studied for detecting and classifying small unmanned aerial vehicles(UAVs). However, small UAVs have translational motion(TM) as well as micro-motion in practical environments. Radar line of sight(LOS) can also be different for the position of a small UAV. The TM and LOS components cause changes of micro-motion properties, necessitating study on the effects of the TM and LOS on the micro-motion signal. In this study, we modeled signals of a maneuvering small UAV and analyzed the micro-motion signal by utilizing the frequency spectrum and spectrogram. Finally, we acquired measurement data of a small UAV having different TM and LOS to analyze their effects on the micro-motion signal.

Keywords: Radar Signal Processing; Micro-Doppler; Small UAV; Frequency Spectrum; Spectrogram

Ⅰ. 서 론

최근 소형 무인기의 조작이 간편해지고 가격이 저렴해지면서 많은 분야에 활용되고 있다. 소형 무인기의 초기 개발 목적인 국가안보뿐만 아니라, 소방차량 진입이 힘든 지형에서의 화재진압, 넓은 토지의 농작물 경작, 영화제작 등 광범위하게 활용되고 있으며, 개인 여가생활에도 이용되고 있다. 하지만 이런 긍정적인 요소와 함께 소형 무인기를 이용한 테러, 사생활 침해와 같은 각종 범죄에 악용될 우려가 함께 증가하고 있다. 따라서 사전에 소형 무인기를 탐지 및 식별하여 발생할 수 있는 문제를 예방하는 것이 매우 중요하다.

소형 무인기는 비행기 혹은 전투기 등의 기존 표적보다 레이다 단면적(radar cross-section: RCS)이 낮으며, 저고도 저속 비행을 한다. 따라서 기존의 탐지 및 식별 방식^[1]～^[3]과는 다른 형태의 연구가 요구된다. 소형 무인기는 로터(rotor)와 날개의 회전을 이용하여 기동하는데, 이런 회전 성분은 소형 무인기가 고유한 미세운동 성분을 갖게 한다. 따라서 소형 무인기의 고유 미세운동 성분을 이용한 탐지 및 식별 연구가 활발하게 진행되고 있다^[4-6].

하지만 미세운동 신호의 특성은 관측각도 변화와 병진운동 성분에 의해 변할 수 있다^[7]. 소형 무인기가 운용되는 실제 환경에서는 미세운동 성분뿐만 아니라, 병진운동 성분이 함께 존재하며, 관측각도 역시 가변할 수 있다. 따라서 미세운동 성분을 이용한 탐지 및 식별을 수행하기 이전에 병진운동과 관측각도 성분이 미세운동 신호에 미치는 영향을 분석하는 연구가 필수적으로 수행되어야 한다.

본 논문에서는 실측 데이터를 기반하여 미세운동 신호의 주요 특성들을 분석하고 나아가 병진운동과 관측각도 변화가 미세운동 신호에 미치는 영향을 분석하였다. 이를 위해 소형 무인기의 실제 기동 환경을 고려한 신호 모델링을 수행하였으며^[7],^[8], 높은 펄스 반복 주파수로(pulse repetition frequency: PRF)로 운용이 가능한 X밴드 레이다를 이용하여 다양한 시나리오에서 소형 무인기의 미세운동 성분을 측정하였다. 최종적으로 실측 데이터의 주파수 스펙트럼과 스펙트로그램을 획득하였으며, 이를 바탕으로 미세운동 신호 특성을 분석함으로써 병진운동과 관측각도가 미세운동 성분에 미치는 영향을 성공적으로 분석할 수 있었다.

Ⅱ. 실제 기동 환경을 고려한 소형 무인기 신호 모델

소형 무인기의 실제 기동 환경을 고려한 점산란원 기하 구조는 다음 그림 1과 같다. 점산란원 P는 z축을 중심으로 ω의 각속도로 회전하며, 이때 점산란원 P와 원점 O 사이의 거리는 r, 점 P의 초기위상은 φ₀이다. 레이다의 시선방향(line of sight: LOS)과 날개의 회전 평면 사이의 각도는 θ이고, 레이다와 원점 O사이의 거리는 R_T(t)이다. 레이다 시선방향의 벡터 성분을 xy평면에 정사영(projection)한 결과가 x축에 존재할 경우, 산란점 P와 레이다 사이의 거리는 다음과 같이 나타낼 수 있다^[8].

그림 1. | Fig. 1. 실제 환경을 고려한 점산란원 기하구조 | Geometry of pointer scatterer in the practical environment.

Download Original Figure

R (t) = R T (t) 2 + r 2 − 2 R T (t) r cos (θ) cos (ω t + ϕ 0)

(1)

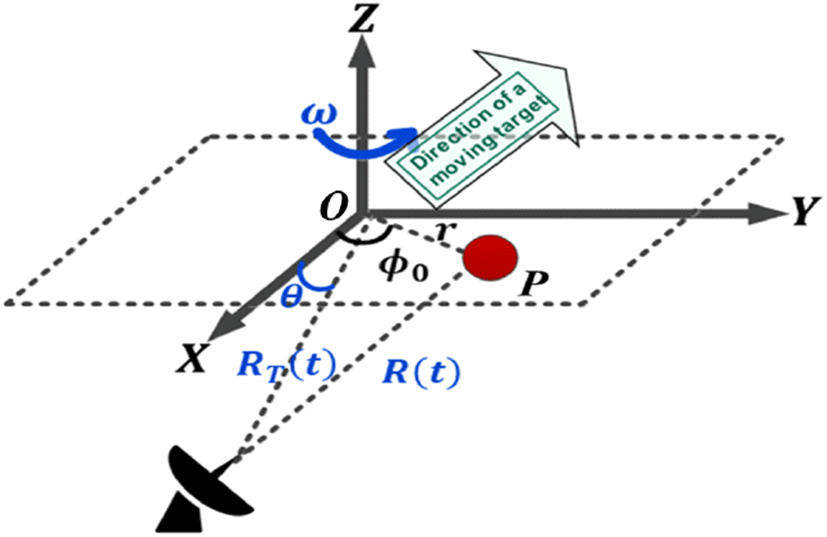
이때 R_T(t)≫r을 만족하는 경우, 식 (1)은 다음과 같이 표현될 수 있다.

R (t) ≈ R T (t) − r cos (θ) cos (ω t + ϕ 0)

(2)

여기서, R_T(t)는 병진운동 성분에 의해 결정되는 거리 값이며 rcos(θ)cos(ωt+φ₀)는 미세운동 성분과 레이다 관측각도에 의해 결정되는 거리 값이다. 즉, 산란점의 위치정보는 병진운동과 미세운동 성분의 선형결합으로 표현된다.

R (t) = R T (t) + R M (t)

(3)

위 식에서 R_T(t)와 R_M(t)는 다음과 같다.

R T (t) = R 0 + v t + 12 α t 2

(4)

R M (t) = − r cos (θ) cos (ω t + ϕ 0)

(5)

여기서, R₀는 레이다와 원점 O사이의 초기 거리이며, v와 α는 각각 레이다 시선벡터 방향의 속도 및 가속도 성분이다.

소형 무인기의 강체(rigid body), 로터(rotor) 그리고 단일 로터에 연결된 날개의 개수가 각각 K, L 그리고 N개 일 때 병진운동과 미세운동을 고려한 소형 무인기의 수신 신호는 다음과 같이 나타낼 수 있다.

s (t) = ∑ k = 1 K A k exp (− j 4 π λ R T ⋅ k (t)) + ∑ l = 1 L ∑ n = − 1 N B l ⋅ n exp [− j 4 π λ {R T ⋅ l (t) + R M l ⋅ n (t)}]

(6)

여기서 A_k는 k번째 강체 산란점의 크기, B_l.n은 l번째 로터에 달려있는 n번째 날개의 산란점 크기 정보이다. R_T.k(t)와 R_T.l(t)는 병진운동에 의해 결정되는 각 산란점의 위치정보이며, $R M l ⋅ n (t)$ 는 각 산란점의 미세운동에 의해 결정되는 위치정보이다.

Ⅲ. 미세운동 신호 특성 분석

3-1 주파수 스펙트럼 분포 특성 분석

병진운동 성분에 의해 결정되는 위상정보는 식 (4)와 식 (6)을 이용하여 다음과 같이 나타낼 수 있다.

s T (t) = exp {− j 4 π λ (v t + 12 α t 2)}

(7)

위 식에서 시간 t에 대해 상수인 성분은 생략하였다. 식 (7)의 푸리에 변환은 다음과 같이 나타낼 수 있다.

S T (f) = δ (f − 2 v λ) * F T [exp (j 2 π λ α t 2)]

(8)

여기서 δ( )는 델타함수, *는 컨볼루션 연산을 나타내며, FT는 푸리에 변환을 나타낸다. 위 식에서 확인할 수 있는 바와 같이 병진운동의 속도성분은 주파수 스펙트럼단에서 주파수 이동을 발생시키는 성분이다. 이에 반해 가속도 정보는 주파수 정보를 퍼지게 하는 성분이다^[9].

식 (5)와 식 (6)을 이용하여 나타낸 미세운동 성분의 위상정보는 다음과 같다.

s M (t) = exp {4 π λ (r cos (θ) cos (ω t + ϕ))}

(9)

위 식의 푸리에 변환은 다음과 같다^[10].

S M (f) = ∑ p = − ∞ ∞ J k (β) δ (f − N ω 2 π p)

(10)

여기서 J_k(β)는 k번째 제 1종 베셀함수이고, β는 4 πrcos(θ)/λ이다. 만약 β≫1이라면 미세운동 신호는 넓은 영역에 에너지가 분포하게 된다. 이때 주파수 밴드의 범위는 다음과 같다^[10].

[f d . min, f d . max] = [− β ω / (2 π), β ω / (2 π)]

(11)

위 결과에서 확인할 수 있는 바와 같이 주파수 밴드의 범위는 날개의 회전속도 ω와 관측각도 θ값에 의해 결정되며, 병진운동 성분은 영향을 받지 않는 것을 확인할 수 있다. 또한 미세운동 신호는 넓은 주파수 범위에 특정 주파수 간격으로 하모닉하게 분포함을 확인할 수 있다. 여기서 하모닉 신호의 기본(fundamental) 주파수인 쵸핑주파수(chopping)는 다음과 같다.

Chopping frequency = N ω 2 π

(12)

쵸핑 주파수는 병진운동 성분과 관측각도에 영향을 받지 않으며, 날개의 개수와 날개의 회전 속도에만 영향을 받는 것을 확인할 수 있다.

식 (7)과 식 (9)를 식 (6)에 대입하면 소형 무인기의 신호는 다음과 같이 나타낼 수 있다.

s (t) = ∑ k = 1 K A k s T . k (t) + ∑ l = 1 L ∑ n = 1 N B l . n s T . l (t) s M . l . n (t)

(13)

식 (13)의 푸리에 변환 결과는 다음과 같이 표현될 수 있다.

s (t) = ∑ k = 1 K A k S T (f) + ∑ l = 1 L ∑ n = 1 N B l . n S T . l (f) * S M l . n (f)

(14)

날개의 산란점은 병진운동 성분과 미세운동 성분의 컨볼루션 형태로 분포함을 확인할 수 있다.

3-2 스펙트로그램 분포 특성 분석

스펙트로그램은 식 (15)와 같이 정의된다.

S T F T (t, f) = | ∫ − ∞ ∞ w (τ − t) s (τ) exp (− j 2 π f τ) d τ |

(15)

여기서 w(τ-t)는 윈도우 함수이고, s(τ)는 소형무인기로부터 수신된 신호이다. 스펙트로그램은 시간-주파수 영상을 획득하기 위해 가장 널리 쓰이는 방법으로 시간 변화에 따른 도플러 주파수 변화를 확인할 수 있다. 위 식 (7)과 (9)에 나타나 있는 병진운동과 미세운동 신호에 위상 편차를 수행하여 획득한 시간 변화에 따른 도플러 주파수는 각각 다음과 같다.

f d . T (t) = 2 λ {v + 12 α t}

(16)

f d . M = − 2 λ {ω r cos (θ) sin (ω t + ϕ 0)}

(17)

병진운동 성분에 의해 형성되는 도플러 주파수는 위 식 (16)에서 볼 수 있는 바와 같이 레이다 시선방향의 속도성분에 의해 상수값을 가지고 가속도 성분에 의해 시간에 따라 선형적으로 변하는 것을 확인할 수 있다. 미세운동 신호로부터 획득한 도플러 주파수는 식 (17)에서 보여지는 바와 같이 날개의 각속도 ω에 의해 결정되는 정현파임을 확인할 수 있다. 최대 도플러 주파수는 sin(ωt+φ₀)가 최대가 되는 경우이며, 이때의 결과는 (11)과 동일함을 확인할 수 있다. 최종적으로 식 (13)에서 확인할 수 있는 바와 같이 강체의 미세 도플러 신호는 병진운동 성분에 의해 결정되며, 날개의 미세 도플러 신호는 병진운동과 미세운동의 합으로 나타남을 확인할 수 있다.

Ⅳ. 실제 측정 데이터를 이용한 미세운동 성분 분석

주파수 스펙트럼과 스펙트로그램단의 미세운동 신호의 특성은 소형 무인기 탐지 및 식별에 활용될 수 있는 중요한 요소이다. 따라서 본 절에서는 실측 데이터를 바탕으로 미세운동 특성을 분석하고, 나아가 병진운동 및 관측각도 성분이 미세운동 신호에 미치는 영향을 분석하였다.

소형 무인기의 실측 데이터 확보를 위해 X밴드 레이다 시스템(그림 2, 표 1)을 구축하였으며, 본 레이다는 첩(chirp) 레이다 시스템으로 송/수신된 신호에 정합필터링(matched filtering) 과정을 수행하여 레인지 프로파일을 획득하였다^[9]. 이후 표적이 존재하는 레인지 빈을 선택하여 주파수 스펙트럼 및 스펙트로그램을 획득하였다. 소형 무인기 날개의 회전 속도는 최대 8,000 RPM으로 알려져 있다. 이를 고려하여 펄스 반복 주파수(pulse repeatition frequency: PRF)는 20 kHz로 설계하였으며, 총 0.1 s 동안 측정하였다. Atmega 128 마이크로 프로세서를 이용한 트리거 신호를 이용하여 임의파형 발생기(abitrary waveform generator: AWG)를 통해 형성된 아날로그 신호부터 수신단을 거쳐 최종적으로 저장되는 디지털 신호의 동기화를 맞추었으며, 임의파형 발생기 내부 클락(clock)을 이용하여 각 펄스들의 동기를 맞추었다.

그림 2. | Fig. 2. 레이다 장비 및 블록다이어그램 | Radar device and block digram.

Download Original Figure

표 1. | Table 1. 레이다 스펙 | Specification of the radar.

Center frequency	10 GHz
Bandwidth	20 MHz
Pulse repetition frequency	20 kHz
Measured time	0.2 sec
Sampling frequency	65 MHz
Transmission power	29.8 dBm(max)
Antenna beam width	20°
Antenna gain	20 dB

Download Excel Table

먼저 관측각도 θ가 0°이고, 제자리 비행(hovering)하는 고정익을 측정하여 이상적인 경우 미세운동 성분 특성 분석을 수행하였다(그림 3). 측정 데이터 획득을 위해 이용된 회전익의 기종은 DJI社의 팬텀 4로 로터의 개수는 네 개이며, 각 로터에는 위상이 반대인 두 개의 날개가 달려있는 기종이다. 회전익 날개의 길이는 12 cm이며, 회전익이 저고도에서 제자리 비행을 할 때 비접촉식 회전계를 이용하여 측정한 날개의 회전 횟수는 약 4,800 RPM(ω=503 rad/s)이었다. 이때 자기상관함수^[11], 임계값 설정 기법^[12],^[13]을 이용하여 주파수 스펙트럼과 스펙트로그램단 특성 분석을 수행하였다. 먼저 자기상관함수기법은 잡음 대비 신호의 세기를 높이기 위해 수행하였으며, 잡음이 존재하는 환경에서 각 파라미터를 추정하기 위해 임계값 설정 기법^[12]을 이용하였다. 본 논문에서는 오 경보율이 10⁻⁴인 경우 형성되는 임계값을 이용하여 임계값이 넘은 신호의 최대 범위를 최대 도플러 주파수, 임계값을 넘은 신호의 간격을 쵸핑 주파수 및 주기 신호로 추정하였다.

그림 3. | Fig. 3. 회전익 측정 환경 | Measurement setup to small UAV.

Download Original Figure

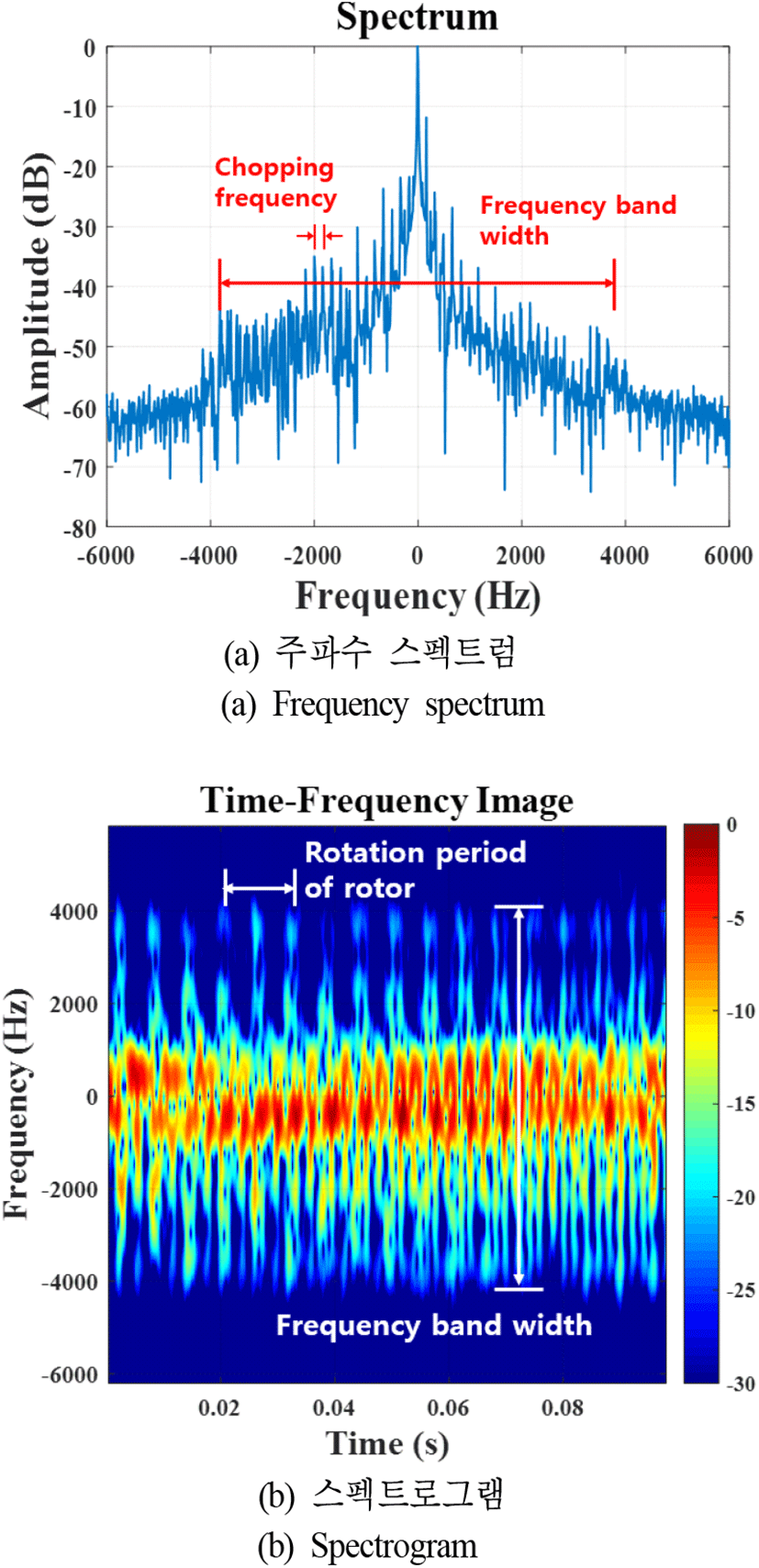
먼저 제자리 비행을 하는 경우의 주파수 스펙트럼(그림 4(a))은 임펄스 신호가 주기적으로 형성되며, 넓은 주파수 영역에 걸쳐 분포하는 것을 확인할 수 있다. 이는 Ⅲ절에서 유도한 주파수 스펙트럼 특성과 일치한다. 강체의 신호는 0 Hz에 형성되었고, 미세운동에 의해 형성된 주파수 밴드의 영역은 [-3,800 Hz, 3,800 Hz]이고, 임펄스 신호의 간격은 170 Hz였다. 이론값을 확인하기 위해 식 (11)에 변수들을 대입하여 획득한 주파수 밴드 영역은 [-4,024 Hz, 4,024 Hz]이고, 식 (12)을 이용하여 획득한 쵸핑 주파수는 160 Hz으로 측정값과 이론값의 오차는 각각 5.6 %와 6 %였다. 스펙트로그램 단에서 형성된 미세운동 신호는 그림 4(b)와 같다. 이때 미세 도플러 신호는 특정 시점에서 넓은 주파수 영역에 분포하며, 이러한 신호가 주기적으로 나타남을 확인할 수 있었다. 이는 최대 도플러 주파 수가 최대일 때 날개의 레이다 단면적이 가장 크기 때문으로 예상할 수 있다^[14]. 스펙트로그램 단에서 동일 날개로부터 획득된 신호의 주기는 0.0115 s(ω=546 rad/s)였으며, 이론값과의 오차는 약 7 %였다. 또한 최대 도플러 주파수는 3,900 Hz로 약 2.5 %의 오차로 매우 정확하게 추정되었다. 각 파라미터의 이론값과 오차값의 발생 원인으로는 비접촉식 회전계의 측정 오차, 레이다와 소형 무인기의 관측각도에 의해 발생하는 오차, 잡음신호에 의해 발생하는 추정 오차 등으로 생각할 수 있다. 하지만 물리적인 원인에 의한 오차를 고려할 경우 각 파라미터의 추정 결과는 신뢰할 수 있는 수준으로 판단할 수 있다. 하지만 표적의 속도 또는 관측각도 변화에 따라 각각의 파라미터 특성이 변할 수 있기 때문에 이를 고려한 분석이 필요하다.

그림 4. | Fig. 4. 미세운동 특성 분석: θ=0°, v=0 m/s, α=0 m/s² | Micro-motion characteristic analysis: θ=0°, v=0 m/s, α=0 m/s².

Download Original Figure

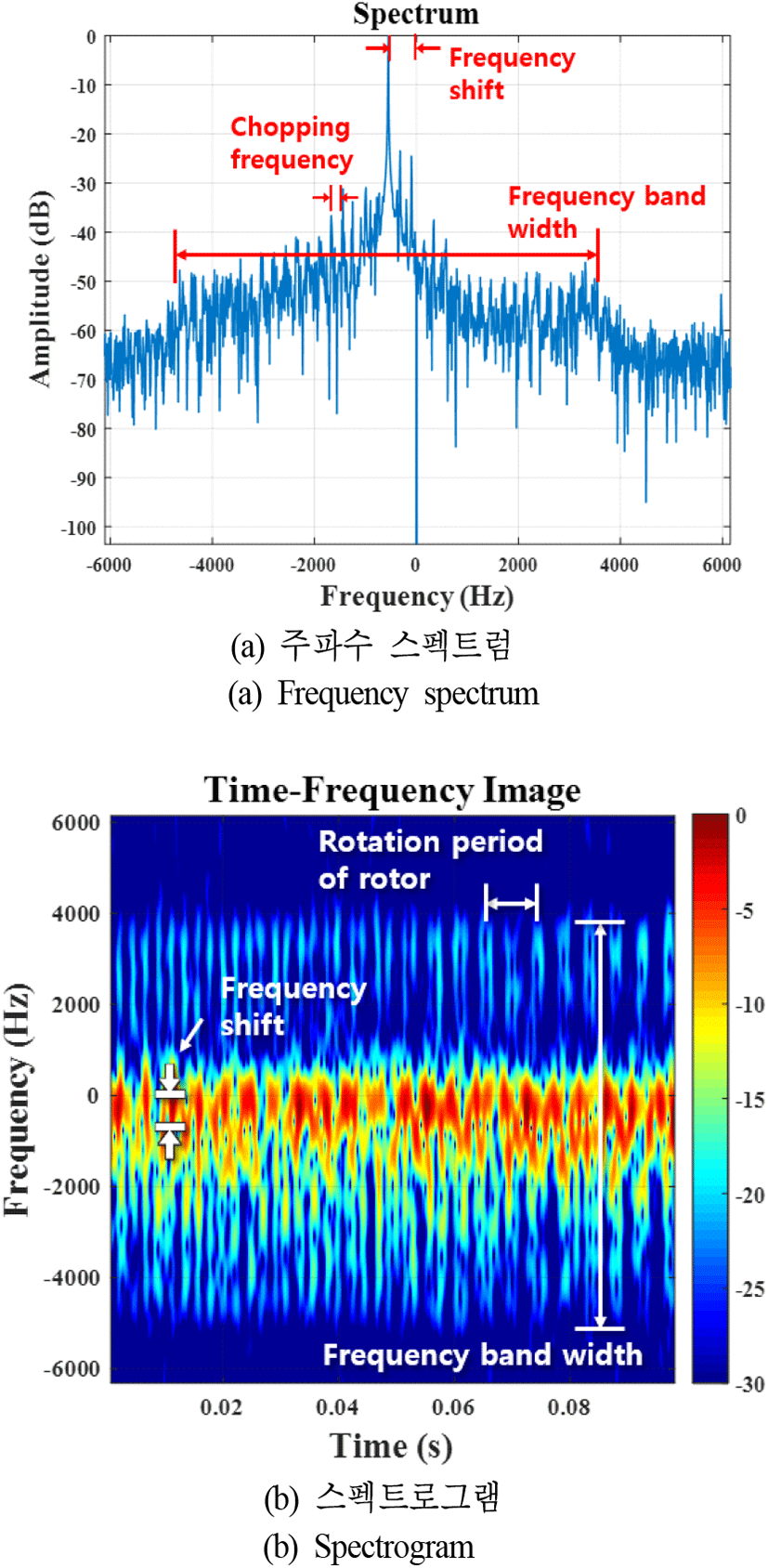
먼저 병진운동 성분이 미세운동 신호 특성에 미치는 영향을 분석하였다. 속도 및 가속도는 DJI社에서 제공하는 기본 앱을 이용하여 측정하였으며, 측정 시 회전익의 속도는 -8 m/s이고, 가속도는 -2 m/s였다. 병진운동 성분이 존재할 경우, 주파수 스펙트럼 및 스펙트로그램의 결과는 그림 5와 같다. 먼저 주파수 스펙트럼(그림 5(a))단에서 강체의 신호는 -550 Hz에 위치하였으며, 이를 중심으로 미세운동 성분이 임펄스 형태로 넓은 주파수 영역에 분포함을 확인할 수 있었다. 이때 주파수 밴드의 범위는 [-4,580 Hz, 3,310 Hz]로 주파수 이동 현상을 제외하면 병진운동 성분이 존재하지 않는 경우 그림 4(a)와 유사한 것을 확인할 수 있었다. 또한 식 (16)을 이용하여 획득한 주파수 이동 값은 -533 Hz로 측정값 -550 Hz와의 오차는 약 3 %였다. 가속도가 2 m/s2이고 측정 시간이 0.1 s인 경우, 식 (16)에서 보여지는 바와 같이 주파수 퍼짐은 약 13 Hz로 매우 낮다. 따라서 위 시나리오와 같이 가속도 성분이 크지 않고 측정 시간에 매우 짧을 경우 그림 4(a)에서 확인할 수 있는 바와 같이 가속도 성분에 의한 퍼짐이 매우 적음을 확인할 수 있었다. 스펙트로그램(그림 4(b)) 결과, 역시 속도 성분에 의해 주파수 이동이 발생하였으며, 이때 주파수 밴드의 범위는 [-4,609 Hz, 3,600 Hz]였고, 중심 주파수는 -504 Hz로 각각 2 %와 2 5 %의 오차값을 가졌다. 하지만 가속도 성분에 의한 기울기 현상은 확인할 수 없었다. 또한 그림 4(b)와 마찬가지로 주기적인 신호가 나타나는 것을 확인할 수 있었으며, 날개의 회전 주기 신호는 약 0.011 s(ω=571 rad/s)로 오차는 약 13 %였다.

그림 5. | Fig. 5. 미세운동 특성 분석: θ=0°, v=-8 m/s, α=-2 m/s² | Micro-motion characteristic analysis: θ=0°, v=-8 m/s, α=-2 m/s².

Download Original Figure

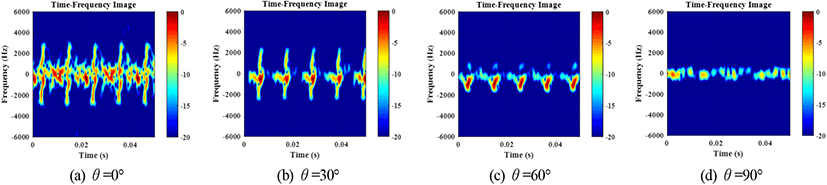
마지막으로 관측각도 변화에 따른 미세운동 성분 특성 분석을 위해 유전율이 공기와 유사한 스티로폼 위에 고정익을 올려둔 다음 고정익의 시선방향을 30°씩 옮겨가며 측정하였다(그림 6). 이때 고정익의 시선방향을 바꾸기 위해 각도가 그려진 나무 원판을 이용하였다. 고정익 날개의 길이는 15 cm였으며, 비접촉식 회전계를 이용하여 측정된 로터의 RPM은 대략 2,700번(ω=283 rad/s)이었다. 고정익을 이용하여 획득한 주파수 스펙트럼(그림 7)은 회전익의 측정 결과와 마찬가지로 넓은 주파수 영역에 걸쳐 임펄스 신호가 형성됨을 확인할 수 있었다. 관측각도 θ가 90°인 경우 임펄스 신호를 확인할 수 없었으며, 이를 제외한 결과에서 쵸핑 주파수는 모두 96 Hz(ω=302 rad/s)로 측정되었으며, 이론값과의 오차는 약 7 %였다. 스펙트로그램(그림 8)단 역시 관측각도 θ가 90°인 경우 미세 도플러 성분을 확인할 수 없었으며, 이를 제외한 경우 주기는 모두 0.021 s(ω=302 rad/s)로 측정되었으며, 이론값과의 오차는 약 6 %였다. 즉, 주파수 스펙트럼단의 쵸핑 주파수값과 스펙트로그램단의 도플러 신호의 주기는 관측각도에 상관없이 동일함을 확인할 수 있었다. 관측각도 변화에 따른 주파수 밴드 영역의 변화는 표 2와 같다. 이때 식 (11)1을 이용하여 이론값을 결정하였으며, 주파수 스펙트럼과 스펙트로그램 영상 각각의 결과를 이용하여 측정값을 획득하였다. 이론값과 측정값 모두 관측각도 θ가 0°인 경우 최대 도플러 주파수 값이 가장 큰 것 을 확인할 수 있다. 또한 관측각도 θ값이 커짐에 따라 최대 도플러 주파수가 작아지는 것을 확인할 수 있었는데, 이는 식 (11)에서 확인할 수 있는 바와 같이 최대 도플러 주파수 값이 cos(θ)값만큼 조정(scaling)되기 때문으로 예측할 수 있다. 관측 각도 θ값이 90°인 경우 표 1에서 확인할 수 있는바와 같이 주파수 밴드의 이론값은 0 Hz이지만, 주파수 스펙트럼의 측정값은 320 Hz, 스펙트로그램의 측정값은 450 Hz였다. 이는 관측각도의 오차 혹은 날개의 기하구조에 의한 것으로 보인다. 하지만 관측각도 θ의 변화에 따른 미세 운동 측정 결과, 주파수 밴드의 범위의 변화는 식 (11)과 유사한 형태로 변화함을 확인할 수 있었다.

그림 6. | Fig. 6. 고정익 측정 환경 | Measurement setup to small fixed-wing UAV.

Download Original Figure

그림 7. | Fig. 7. 관측각도 변화에 따른 주파수 스펙트럼 | Frequency spectrum caused by aspect angle.

Download Original Figure

그림 8. | Fig. 8. 관측각도 변화에 따른 스펙트로그램 | Frequency spectrogram caused by aspect angle.

Download Original Figure

표 2. | Table 2. 알고리즘 비교 분석 결과 | Estimated information between genetic algorithm and propoesd algorithm.

Degree(°)	Theoretical value(Hz)	Measured value (Hz)	Error(%)	Measured value (Hz)	Error(%)
Degree(°)	Theoretical value(Hz)	Frequency spectrum		Spectrogram
0	2,827	2,640	6.6	2,650	6.2
30	2,449	2,322	5.2	2,250	8.1
60	1,414	1,470	4.0	1,500	6.1
90	0	320	-	450	-

Download Excel Table

Ⅴ. 결 론

본 논문에서는 실측 데이터를 바탕으로 미세운동 신호의 특성을 분석하고, 나아가 병진운동과 관측각도 성분이 미세운동 신호에 미치는 영향을 분석하였다. 먼저 실제 기동환경을 고려하여 소형 무인기 신호 모델링을 수행하였으며, 주파수 스펙트럼 및 스펙트로그램단에서 나타나는 미세운동 신호 특성을 분석하였다. 최종적으로 실제 측정 데이터를 바탕으로 병진운동과 관측각도 성분이 미세운동 신호 특성에 미치는 영향 분석을 주파수 스펙트럼 및 스펙트로그램 단에서 성공적으로 수행하였다.

본 연구를 통해 소형 무인기의 실제 기동 환경을 고려하여 미세운동 신호를 성공적으로 획득할 수 있었다. 이러한 결과를 이용하여 기존에 존재하는 탐지 및 식별 기법에 적용할 경우 예상하지 못한 결과가 발생할 수 있다. 따라서 본 연구자들은 추후 본 측정 결과를 바탕으로 탐지 및 식별 알고리즘에 적용하여 결과를 도출할 예정이며, 추후 발생하는 문제점을 분석 및 보완할 예정이다.

Acknowledgements

「이 연구는 국방과학연구소가 지원하는 위협표적 모델링 및 특성분석 사업의 일환으로 수행되었습니다.」

References

[1].

W. Y. Song, S. H. Rho, C. H. Jung, and Y. K. Kwag, “Synthetic aperture radar target detection using multi-cell averaging CFAR scheme,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 21, no. 2, pp. 164-169, Feb. 2010.

[2].

M. A. Richards, Fundamentals of Radar Signal Processing, Chicago, McGraw-Hill, pp. 347-381, 2005.

[3].

F. C. Robey, D. R. Fuhrmann, E. J. Kelly, and R. Nitzberg, “A CFAR adaptive matched filter detector,” in IEEE Transactions on Aerospace and Electronic Systems, vol. 28, no. 1, pp. 208-216, Jan 1992.

[4].

P. Molchanov, R. I. A. Harmanny, J. J. M. de Wit, K. Egiazarian, and J. Astola, “Classification of small UAVs and birds by micro-Doppler signatures,” in 2013 European Radar Conference, Nuremberg, 2013, pp. 172-175.

[5].

P. Zhang, L. Yang, G. Chen, and G. Li, “Classification of drones based on micro-Doppler signatures with dual-band radar sensors,” in 2017 Progress in Electromagnetics Research Symposium - Fall (PIERS - FALL), Singapore, 2017, pp. 638-643.

[6].

W. Zhang, G. Li, “Detection of multiple micro-drones via cadence velocity diagram analysis,” in Electronics Letters, vol. 54, no. 7, pp. 441-443, Apr. 2018.

[7].

K. B. Kang, S. G. Sun, J. S. Lee, B. R. Jo, S. H. Park, and K. T. Kim., “Analysis of micro motion signal characteristics of small UAV based on actual data,” in 2018 The Korean Institute of Electromagnetic Engineering and Science(KIEES) SummerConference, Aug. 2018, vol. 6, no. 1.

[8].

A. Xiaofeng, Z. Xiaohai, Y. Jianhua, L. Jin, and L. Yongzhen, “Feature extraction of rotating target based on bistatic micro-Doppler analysis,” in Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, Oct. 2011, pp. 609-612.

[9].

C. Ozdemir, Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms, Hoboken, NJ, John Wiley & Sons, pp. 133-139, 2012.

[10].

M. R. Bell, R. A. Grubbs, “JEM modeling and measurement for radar target identification,” IEEE Transactions on Aerospace and Electronic Systems, vol. 29, no. 1, pp. 73-87, Jan. 1993.

[11].

P. Tait, Introduction to Radar Target Recognition, The Institution of Engineering and Technology, pp. 183-218, 2006.

[12].

M. A. Richards, Fundamentals of Radar Signal Processing, Chicago, IL, McGraw-Hill, pp. 347-383, 2005.

[13].

L. Du, L. Li, B. Wang, and J. Xiao, “Micro-Doppler feature extraction based on time-frequency spectrogram for ground moving targets classification with low-resolution radar,” IEEE Sensors Journal, vol. 16, no. 10, pp. 3756-3763, May 2016.

[14].

V. C. Chen, The Micro-Doppler Effect in Radar, Boston, MA, Artech House, pp. 93-143, 2011.