The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2019; 30(6):507-517

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2019.30.6.507

논문/REGULAR PAPERS

다기능 레이다를 이용한 저 RCS 해상표적 탐지성능 분석

이명준

, 김지은

, 이상민

, 전현무^*

, 양우용^*

, 김경태^†

Detection of Low-RCS Targets in Sea-Clutter using Multi-Function Radar

Myung-Jun Lee

, Ji-eun Kim

, Sang-Min Lee

, Hyeon-Mu Jeon^*

, Woo-Yong Yang^*

, Kyung-Tae Kim^†

한국방송통신전파진흥원 전파자원개발팀

¹한화시스템

Spectrum Refarming Team, Korea Communications Agency

¹Hanwha System

^†Corresponding Author: Kyung-Tae Kim (e-mail: kkt@postech.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: May 14, 2019; Revised: Jun 07, 2019; Accepted: Jun 14, 2019

Published Online: Jun 30, 2019

요약

다기능 레이다(multi-function radar: MFR)는 탐지, 추적, 식별 등 다양한 기능을 동시에 수행하는 레이다 시스템이다. 이러한 MFR은 여러 기능을 실시간 내에 수행해야 하기 때문에, 탐지 모드를 위한 측정 시간이 매우 짧은 특징을 갖고 있다. 또한, 저 레이다 단면적(radar cross section: RCS)을 갖는 해상표적을 탐지하기 위해 개발된 기존의 다양한 탐지기법들이 존재하며, 해당 기법들을 MFR 탐지모드에도 사용할 수 있다. 그러나 기존에 연구된 많은 해상표적 탐지기법은 상대적으로 긴 시간 측정된 해상 신호에 대해 효과적 해상표적 탐지가 가능하도록 개발되었기 때문에, 매우 짧은 측정 시간을 갖는 MFR 탐지 모드에는 적합하지 않은 부분이 있다. 본 논문에서는 MFR 탐지 모드의 짧은 측정 시간을 고려한 해상클러터 모델링 방법을 제시하고, 이를 이용하여 해상 클러터 신호를 생성하였다. 또한 해상표적 RCS를 수치해석 기법을 이용하여 계산하고, 앞에서 계산된 클러터 신호와 결합하였다. 이렇게 생성된 최종 레이다 수신 신호를 이용하여 기존에 개발된 4가지 서로 다른 해상표적 탐지기법을 적용하고, 탐지성능을 분석하였다.

Abstract

Multi-function radar(MFR) is a system that uses various functions such as detection, tracking, and classification. To operate the functions in real-time, the detection stage in MFR usually uses radar signals for short measurement time. We can utilize several conventional detectors in the MFR system to detect low radar cross section maritime targets in the sea-clutter; however, the detectors, which have been developed to be effective for radar signals measured for a longer time, may be inappropriate for MFR. In this study, we proposed a modelling technique of sea-clutter short measurement time. We combined the modeled sea-clutter signal with the maritime-target signal, which was obtained by the numerical analysis method. Using this combined model, we exploited four independent detectors and analyzed the detection performances.

Keywords: CA-CFAR; EMD; Fractal; MFR; Sea Clutter Model

Ⅰ. 서 론

해상표적 탐지는 해수면 위의 위협체 및 비상상황 관측을 목적으로 사용되고 있으며^[1], 파도와 같은 해상 클러터는 지상 클러터와는 다르게, 시간에 따른 유동성이 존재하는 특성이 있다. 위와 같은 특성들로 인해 지상표적 탐지기법은 해상클러터 내의 표적 탐지에는 불리하며, 이를 극복하기 위하여 해상 표적 탐지에 적합한 많은 탐지기법들^[1]～^[3]이 개발되었다. 특히, 해상클러터를 억제하여 해상표적을 탐지하기 위하여 개발된 탐지기법들은 해상클러터에 대하여 긴 시간 동안(일반적으로 1초 이상) 측정된 레이다 신호에 적합하도록 개발되었다.

레이다 기술이 발전함에 따라 최신 레이다들은 탐지, 추적, 식별 등의 여러 기능들이 하나의 시스템에서 구동되며, 이를 다기능 레이다(multi-function radar: MFR)라고 명칭한다^[4]. 특히, MFR은 다른 기능보다 선행되는 탐지단계의 측정시간을 짧게(일반적으로 0.1초 이하) 갖도록 요구하여 효율적 자원관리를 통한 실시간 운용이 가능하도록 한다. 그러므로, 측정시간이 짧은 MFR 탐지모드에서는 기존에 개발된 해상표적 탐지기법이 적합하지 않을 것으로 예상할 수 있다. 따라서 MFR 탐지모드에 적합한 해상표적 탐지기법 개발에 앞서, MFR 탐지모드에 적용된 기존기법들의 탐지성능 분석이 필요하다. 본 논문에서는 MFR 탐지 시나리오에 적합한 해상클러터 모델링 방법을 제시하고, 수치해석을 통해 획득된 해상 표적 신호를 결합한다. 결합된 레이다 신호에 대하여 기존 4가지 탐지기법을 적용하고, 탐지성능을 분석하였다.

Ⅱ. MFR 탐지에 적합한 해상 클러터 모델링

2-1 해상클러터 특성

일반적으로 해상클러터를 모델링하기 위해 고려하는 해상클러터 특성은 반사도 분포와 도플러 스펙트럼이다. 해수면에는 해상 스파이크가 존재하여 레이다 반사 면적(radar cross section: RCS)이 상대적으로 큰 해상 영역이 존재하며, 특정 레인지 빈에서 레이다 수신 신호의 크기가 큰 값을 갖는다. 해상 스파이크가 많은 클러터일수록 크기분포의 꼬리쪽 비율이 높은 분포로 모델링되며, 모델링된 분포의 모습은 해상상황에 따라서 차이가 있다^[5],^[6].

동시에, 해상 클러터는 바람과 조류의 영향으로 이동하는 특성을 가지고 있으며, 이로부터 각 레인지 빈에 대해서 도플러 신호의 중심축이 0이 아닌 값을 갖는다^[7]. 중심축 위치는 파도의 레이다 가시선 방향(radar line of sight: RLOS)으로의 속도와 연관되며, 이를 모델링함으로써 파도 이동 방향과 속도를 고려한 해상 클러터 모델링이 가능하다.

기존의 두 가지 특성뿐만 아니라, MFR 탐지 시나리오에서 측정되는 해상 클러터 신호는 파도의 파장에 대한 특성이 고려되어야 한다. 일반적으로 파도의 마루에서 측정되는 레이다 단면적 크기는 골에서 측정되는 레이다 단면적보다 큰 값을 지닌다^[8]. 따라서 MFR 탐지 시나리오에 적합한 해상클러터를 모델링하기 위해서는 해상 파도의 파장을 고려해야 한다.

세 가지 해상클러터 특성 (신호 크기분포, 도플러스펙트럼, 해상 파도 파장)을 고려한 모델링 흐름도는 그림 1과 같다. 신호 크기분포와 해상 파도 파장 특성을 고려한 단일 펄스 해상 클러터를 모델링하고, 이를 이용하여 도플러 스펙트럼 특성을 고려한 MFR 탐지모드에서 수신되는 다중 펄스 해상 클러터를 모델링한다.

2-2 해상클러터 모델링–단일 펄스(Single Pulse)

기존의 해상 클러터 모델링은 주로 특정 레인지 빈에서 수신되는 시간 축 데이터를 모델링한다. 그러나, MFR 탐지모드는 수신시간이 짧기 때문에, 해당 시간 동안에 수 신되는 신호의 시간에 따른 크기 변화가 작다^[3]. 따라서, MFR 탐지 시나리오에 적합한 해상 클러터 모델링을 위해서는 넓은 해상 클러터 영역에 대해서 수신되는 단일 펄스 수신 신호를 모델링하는 것이 우선적으로 중요하다.

그림 1. | Fig. 1. 해상 클러터 모델링 흐름도 | Flowchart of sea clutter modeling.

Download Original Figure

해상 클러터 신호의 크기분포 모델링에 대해서 많은 연구가 수행되어 왔다^[6]. K분포는 해상 클러터의 크기분포 모델링 중에 한가지로, 그림 2에서 다른 분포 (Weibull 및 log-normal 분포)와 비교하였을 때, K 분포가 실측 해상 클러터 데이터인 IPIX 데이터를 가장 유사하게 모델링한 것을 볼 수 있다.

f x (x) = 2 b π Γ (v) (b 2 π x) v K v − 1 (π b x)

(1)

f_x(x)는 K분포이며, Γ()는 감마(Gamma) 함수, K_α ()는 차수가 α인 베셀(Bessel) 함수를 의미한다. ν는 K분포의 모양(shape) 매개변수이고, b는 K분포의 크기(scale) 매개변수이다.

해상 클러터는 텍스쳐(texture) 성분과 스펙클(speckle) 성분으로 이루어져 있으며, 텍스쳐 성분은 평균세기를 나타내는 중력파(gravity wave)와 연관된 성분이다. 스페클 성분은 도플러 특성을 반영하는 표면 장력파(capillary wave)와 연관된 성분이다^[9],^[10]. K분포의 해상 클러터를 구성하고 있는 텍스쳐 성분, f_y(y)의 루트 감마(root-Gamma) 분포와 스페클 성분, f(x|y)의 레일리(Rayleigh) 분포는 다 음과 같다.

그림 2. | Fig. 2. 해상클러터 신호 크기 분포 모델링 비교^[6] | Comparison of amplitude statics^[6].

Download Original Figure

f y (y) = g (y), g (y) = 2 b 2 v Γ (v) y 2 v − 1 exp (− b 2 y 2)

(2)

f (x | y) = π x 2 y 2 exp (− π x 2 4 y 2)

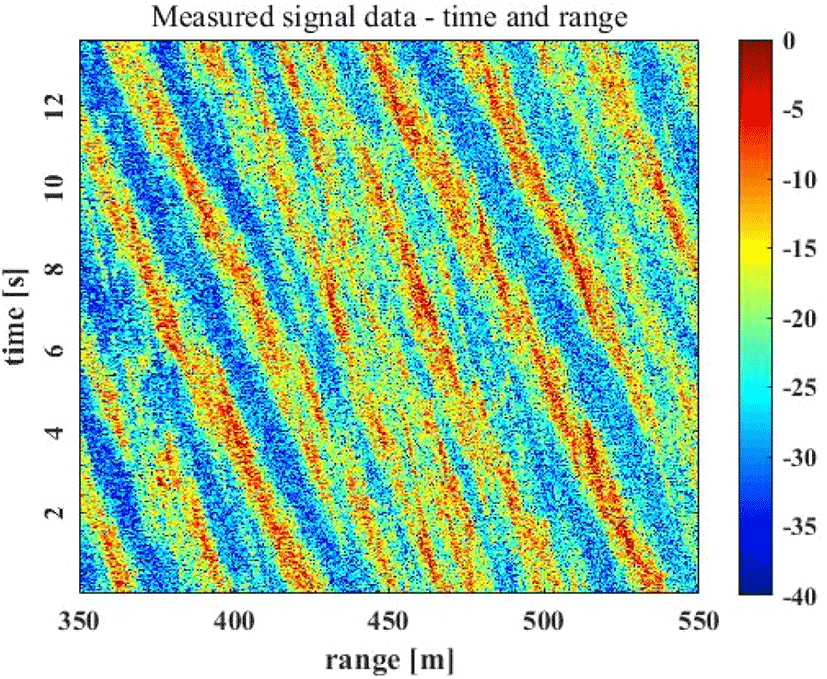
파도의 모습이 해상 클러터 수신신호 모습과 관계가 있음을 그림 3에서 볼 수 있다^[8]. 해상 파도의 주기정보를 포함한 시간 축 해상클러터 모델링을 위해서는 특정 레인지 빈에서의 해상클러터 수신 데이터의 자기상관함수(auto-correlation function: ACF)를 이용하여 모델링이 필요하다^[7]. 반면, MFR 탐지모드에 적합한 해상클러터 모델링을 위해서는 해상 파도의 파장에 대한 정보가 필요하기 때문에, 거리축 해상클러터 수신신호에 대한 ACF 추출이 필요하다. 그러나, 넓은 주파수 대역을 갖는 레이다의 고해상도 거리 프로파일(range profile)에서 관측되는 해상클러터 신호는 파도의 파장 모습뿐만 아니라, 많은 스페클 성분들이 포함되어 있는 것을 그림 4(a)에서 볼 수 있다. 따라서, 저대역 필터를 통과한 해상클러터 신호(그림 4(b))를 이용하여 스페클이 제거된 해상클러터 신호를 획득하고, 이를 이용하여 파도의 파장 정보를 갖는 ACF를 추출할 수 있다.

그림 3. | Fig. 3. 해상클러터에서 보이는 파도 모습 | Shape of sea waves in sea clutter signal.

Download Original Figure

그림 4. | Fig. 4. 해상클러터 신호 거리 프로파일 | Range profile of sea clutter.

Download Original Figure

무기억 비선형 변환(memoryless non-linear transform: MNLT) 기법을 이용해 감마 분포를 갖는 g(y)를 모델링할 수 있으며^[7],^[11], 이를 위해서는 모양 매개변수, υ와 크기 매개변수, b을 고려한 감마 누적분포함수(cumulative distribuiton function: CDF)와 앞서 추출한 거리축 해상 클러터의 ACF를 이용한다. 상기과정을 통해 획득한 감마 분포, g(y)에 제곱근을 적용하여 $g (y)$ 의 해상클러터 텍스쳐성분을 모델링할 수 있다.

스페클 성분은 신호의 실수부와 허수부가 각각 표준편차 $1 / 2$ 를 갖는 가우시안 분포를 가지기 때문에, 신호의 절대값은 레일리분포를 갖는다^[7]. 상기 방법을 통해 모델링된 텍스쳐 성분과 스펙클 성분의 곱을 통해서 거리 축 단일펄스 해상클러터 모델링을 획득할 수 있다.

2-3 해상클러터 모델링–다중 펄스(Multiple Pulses)

MFR 탐지모드에서는 짧은 시간 측정된 레이다 신호를 사용하기 때문에, 적은 개수의 레이다 수신 신호를 이용하게 된다. 수신되는 신호들의 크기는 짧은 시간 동안에 변화가 거의 없기 때문에, 거의 동일한 크기를 갖는 것으로 가정할 수 있다^[8]. 하지만, 각 펄스 간 위상정보 차이는 존재하며, 이로부터 해상클러터에 존재하는 파도의 움직임에 대한 정보가 도플러 스펙트럼의 형태로 표현된다.

파도의 움직임으로부터 발생되는 도플러 스펙트럼 모델링을 위해서는 레인지 빈에서 측정되는 도플러 스펙트럼의 모양을 결정해야 하는데, 해당 모양은 가우시안 모양이라고 가정할 수 있다^[7].

G (f, x, s) = x 2 π s exp [− (f − m f) 2 2 s 2]

(4)

f는 도플러 주파수, m_f는 도플러주파수의 평균, x는 신호의 크기, s는 가우시안 모습 스펙트럼의 표준편차를 의미한다. 따라서 m_f와 s를 추정하고, 해상클러터의 모든 레인지 빈이 해당 스펙트럼을 갖도록 모델링한다.

Ⅲ. 저 RCS 해상 표적 모델링

탐지 성능 분석을 위해서 해상 클러터 내에 존재하는 저 RCS 해상 표적 모델링이 필요하며, 이를 위해 계단식 주파수 파형에 대한 전자파 산란신호, E^s(f)를 수치해석을 통해 획득 후(식 5), 역 고속 푸리에 변환(inverse fast Fourier transfoam: IFFT)을 통해 표적 신호에 대한 거리 프로파일 E^s(x)을 획득할 수 있다^[12](식 6).

E s (f) = ∑ i = 1 N A i e − j 2 k x i = ∑ i = 1 N A i e − j 2 π (2 f c) x i

E s (x) = ∑ i = 1 N A i ⋅ e − j 2 k c (x − x i) sin c (2 B c (x − x i))

획득된 해상표적의 거리 프로파일, E^s(x)이 해상클러터 모델링 내에 존재하도록 결합하기 위해 표적 대 클러터 신호비(signal to clutter ratio: SCR)^[13]를 고려한 E^s(x)의 크기변화(scaling)가 필요하다.

S C R = σ t σ c = σ t σ t S c l u t t e r = P t P c

(7)

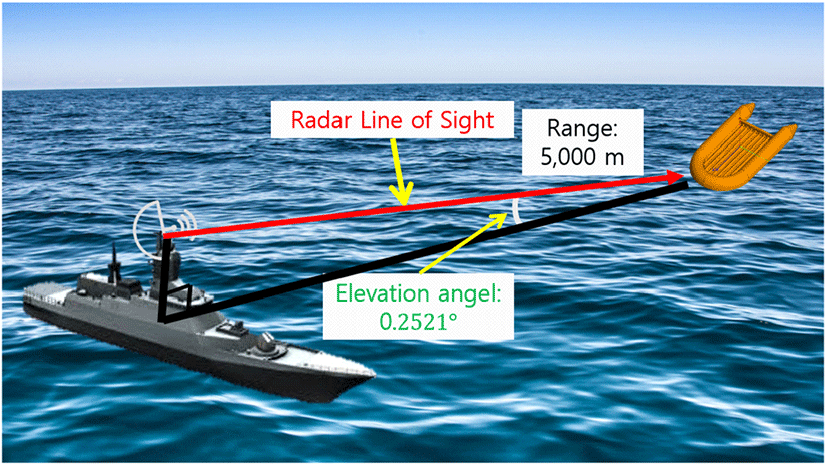
P_t와 P_c는 표적과 클러터 신호의 전력, σ_t와 σ_c는 표적과 클러터의 RCS를 의미한다. 특히, σ_c는 해상 클러터의 단위면적당 후방산란계수인 σ₀와 반사면적인 S_clutter의 곱으로 계산 가능하다. σ_t는 수치해석을 통해서 획득할 수 있으며, σ₀는 Technology Service Corporation(TCS) 모델로부터 획득한다^[14]. S_clutter는 그림 5와 식 (8)을 통해 획득할 수 있으며, 이를 통해 SCR을 계산할 수 있다.

S c l u t t e r = R max 2 − R min 2 2 θ

(8)

P t = S C R × P c = σ t σ c × P c

(9)

그림 5. | Fig. 5. 레이다 해상 클러터 반사 면적 | Reflected surface of radar.

Download Original Figure

R_max와 R_min은 수신 레인지 빈의 최대 및 최소거리, θ는 방위각 방향의 레이다 3 dB 빔 폭을 의미한다. 앞서 모델링된 해상 클러터 신호로부터 계산된 P_c와 SCR로부터 식 (9)을 통해 획득되는 P_t를 갖도록 E^s(x)의 크기변화를 수행하여 해상클러터 모델링과 결합한다.

Ⅳ. 표적 탐지 기법

본 연구에서는 Ⅱ와 Ⅲ에서 제시된 해상클러터 및 해상표적 모델링이 결합된 신호에 대해 기존의 해상표적 탐지기법을 적용하여 탐지성능을 분석한다. 사용된 기법 은 일정오경보율(constant false alarm rate: CFAR)^[15] 탐지기법, 프렉탈(Fractal)^[3] 특성을 이용한 탐지기법, 단일 함수 분해(emperical mode decomposition: EMD)^[1],^[16] 과정을 이용한 탐지기법, 방사형 기본 함수(radial basis function: RBF)를 이용한 신경망 회로(neural network: NN)^[2],^[17] 탐지기법이며, 각각의 추출된 특징 벡터를 이용하여 탐지를 수행한다.

4-1 일정오경보율 기법

CFAR는 일정한 오경보를 갖도록 문턱 값을 설정하여 탐지하는 기법으로 셀 평균 (cell-average: CA) CFAR 탐지기법의 문턱값 설정을 위한 관계는 다음과 같다^[15].

T = β P n

P n = 1 N r ∑ n = 1 N r x n, β = N r (P F A − 1 / N r − 1)

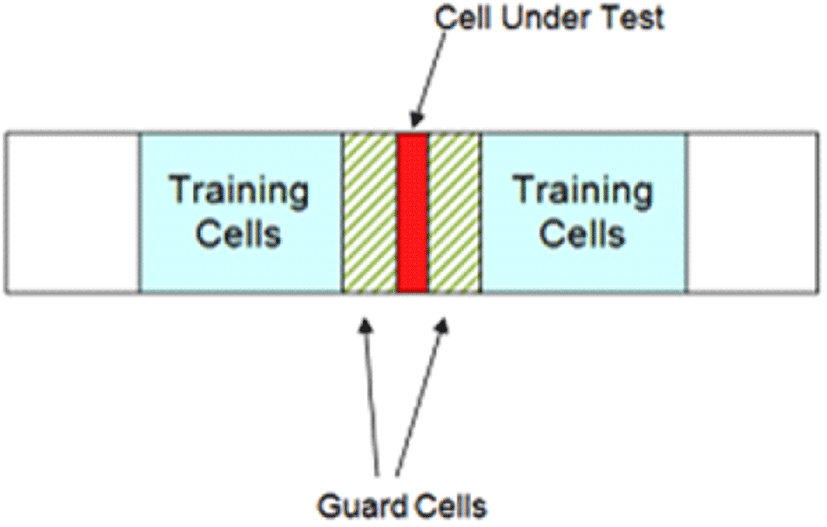
T는 시험 레인지 빈에 설정되는 문턱값, N_r은 훈련 레인지 빈의 개수를 의미하고, x_n은 n번째 훈련 레인지 빈에 수신되는 레이다 신호의 크기, P_FA는 미리 지정된 일정 오경보율이다. 그림 6에서 시험 레인지 빈에 대해서 가드 레인지 빈과 훈련 레인지 빈이 양쪽에 존재하여 해당 훈련 레인지 빈에 수신되는 신호의 크기를 사용하여 시험 레인지 빈에 문턱 값을 설정한다.

그림 6. | Fig. 6. 1차원 일정오경보율 탐지기 구조 | Structure of 1-dimensional CFAR detector.

Download Original Figure

4-2 프랙탈 기법

프랙탈은 부분과 전체가 똑같은 모양을 하고 있다는 자기 유사성 개념을 기하학적 구조를 의미한다. 이런 구조는 자연계의 모습에서 확인할 수 있으며, 해상 클러터가 존재하는 레인지 빈에서 측정되는 레이다신호에서는 프랙탈 특성이 많이 관측되고, 표적이 존재하는 레인지 빈의 수신축 레이다 신호에서는 프랙탈 특성이 상대적으로 적게 관측이 된다. 이를 분석하기 위해서 다중 프랙탈(multi-fractal) 분석기법^[3]을 사용하며, 프랙탈 특성 정량화를 위해 허스트(Hurst) 매개변수를 획득하며, 해당 매개변수는 다음 식 (12)～식 (15)를 통해서 얻는다.

x i = X − μ

(12)

y (n) = ∑ i = 1 n x i

(13)

F q (m) = 〈 | y (n + m) − y (n) | q 〉 1 / q

(14)

H (q) = log m F (q) (m)

(15)

허스트 매개변수는 H(2)를 의미하며, X_i는 시간축 수신 신호크기, μ는 해당 시간배열 레이다 신호 크기의 평균, 〈〉는 평균화 부호, ||는 절대값 부호를 의미한다. 프랙탈 특성이 적은 해상표적에서 허스트 매개변수는 큰 값으로 표현된다.

4-3 단일 함수 분해 기법

반사되어 수신되는 시간 축 레이다 신호는 일반적으로 다양한 주파수의 성분들로 구성되어 있다. 다중 주파수 성분으로 이루어진 신호를 여러 개의 단일 성분 신호(intrinsic mode function: IMF) 로 분해할 때, 최종적으로 존재하는 나머지 함수, 추세함수(trend function)를 이용하면 해상클러터와 해상표적을 분리할 수 있다^[1]. IMF와 추세함수로 이루어진 레이다 신호를 표현하면 다음 식 (16)과 같다^[16]. 초기 최대 신호 크기의 α배 이하의 추세함수 신호 크기를 갖도록 반복한다.

S (t) = ∑ i = 1 n c i (t) + r (t)

(16)

상기 식에서의 S(t)는 시간배열의 레이다 신호, c_i(t)는 n번 수행된 EMD 기법을 통해서 추출되는 각각의 IMF이며, r(t)는 EMD기법을 통해 추출되는 추세함수를 의미한다. 표적신호의 추세함수가 해상 클러터의 추세함수 보다 큰 크기를 가지며, 해당 특징벡터를 이용하여 표적 탐지를 수행할 수 있다.

그림 7. | Fig. 7. 단일 함수 분해 기법 블록 다이어그램^[14] | Block-diagram of EMD^[14].

Download Original Figure

4-4 RBF을 이용한 신경망회로 기법

해상 클러터의 특징에 대한 차원(demension) 정의가 어렵고, 각각 다른 해상 상황에 대한 모델 지정이 어렵기 때문에^[17] 해상 클러터 레이다 신호는 혼돈(chaotic) 특성을 지닌다^[18]. 따라서 혼돈특성인 해상 클러터에 존재하는 해상표적을 탐지하기 위해서 신경망회로 탐지기법을 사용할 수 있으며, 이를 통해 해상클러터의 특징을 비선형적으로 추정할 수 있다.

비선형적 시스템에 적합한 RBF를 활성함수로 갖는 신경망 회로 구성을 위해 필요한 사상함수(mapping function)는 다음 식 (17)과 같이 획득할 수 있다.

R k (x (t − 1)) = exp [− ‖ x (t − 1) − c k ‖ σ k 2]

σ k 2 = d 2 / k

R_k는 K개의 히든 유닛 가운데 k번째 히든 유닛에서 사용되는 사상함수이고, x(t)는 정규화된 t번째 시간에서의 시간배열 클러터 신호이다. c_k는 입력된 훈련 시간배열 클러터 신호가운데 임의의 신호, σ_k는 k번째 히든 유닛에서의 클러터신호의 표준편차, d는 선정된 c_k들 간에 최대거리를 의미한다. 훈련 해상 클러터 신호들을 이용하여 k번째 히든 유닛의 가중치, w_k를 신경망회로를 통하여 학습하고, 이로부터 예측값 $x^(t)$ 를 다음과 같이 획득할 수 있다.

x^(t) = ∑ k = 1 K w k R k (x (t − 1))

(19)

획득된 예측값 $x^(t)$ 와 측정된 수신된 레이다 신호 x(t)의 오차인 ɛ(t)를 계산하며 해상표적일 경우 ɛ(t)가 해상클러터와 비교하여 상대적으로 큰 값을 갖는다.

Ⅴ. 탐지성능 분석 결과

본 논문에서는 해상 클러터와 해상 표적(구명보트)의 레이다 반사 신호를 모델링하고, 해당 레이다 신호에 적용한 서로 다른 네 가지 탐지기법들의 탐지성능을 분석하였다. 시뮬레이션에서 사용한 클러터 및 표적, 레이다, 탐지기법 관련 매개변수는 각각 표 1～표 3 및 그림 8과 같다.

표 1. | Table 1. 시뮬레이션에서 사용한 클러터, 표적 매개변수 | Simulation clutter & target parameters.

Parameter	Value
Range of sea clutter	1,000 m
Information of measured data-location/date	Yeong-duk, South-Korea/24.09.2014
LPF to extract sea clutter waves	Hamming window
Target	Lifeboat
Range of radar to clutter center	5,000 m
CAD tool	VIRAF
Elevation view angle to target	0.2521°
Azimuth view angle to target	−180°～180°
signal-to-noise ratio (SNR)	15 dB
Iteration	100 times

Download Excel Table

표 2. | Table 2. 시뮬레이션에서 사용한 레이다 매개변수 | Simulation radar parameters.

Parameter	Value
Carrier frequency	X-band
Bandwidth	300 MHz
Sampling frequency	750 MHz
Pulse repetition frequency (PRF)	1 kHz
Pulse width	20 μs
# of pulse	32

Download Excel Table

표 3. | Table 3. 시뮬레이션에서 사용한 탐지기법 매개변수 | Simulation detector parameters.

Parameter	Value
Fractal
m	2
EMD
α	10⁻¹⁰
RBF-NN
# of input layer neurons	5
# of hidden layer neurons	15
CA-CFAR
# of guard cells	10
# of training cells	32

Download Excel Table

그림 8. | Fig. 8. 해상 표적 탐지 시뮬레이션 시나리오 | Simulation of marine target detection.

Download Original Figure

실제 측정된 해상 클러터 거리-시간 데이터로부터 ν= 0.3812, b=0.9903으로 추정하였다. 또한, 해밍(Hamming) 윈도우의 저대역 필터를 통과해서 획득한 해상 클러터 신호는 파도의 파장정보를 가지고 있기에 해당 신호로부터 ACF를 그림 9와 같이 획득하였다. 이로부터 단일 펄스 해상 클러터 모델링을 그림 10과 같이 모델링하였다. 신호 대 잡음비(signal to noise ratio: SNR)를 고려한 다중펄스들에 대해서, 추정된 m_f=175 Hz와 s=50 Hz를 갖도록 다중펄스 간의 위상을 설정하였다. 다중 펄스 해상 클러터 모델링은 그림 11과 같다.

그림 9. | Fig. 9. 텍스쳐 모델링을 위한 자기 상관 함수 | ACF for texture modeling.

Download Original Figure

그림 10. | Fig. 10. 단일 펄스 해상 클러터 모델링 | Sea clutter modeling of single pulse.

Download Original Figure

그림 11. | Fig. 11. 다중 펄스 해상 클러터 모델링 | Sea clutter modeling of multi pulses.

Download Original Figure

모델링된 클러터의 σ₀=1.39×10^-5 m²/m² 및 S_clutter=26,173 m2로부터, σ_c=3.64×10-1 m2를 계산할 수 있으며, 100회의 반복 수행 동안에 표적에 대한 관측 방위각 (azimuth view angle)은 무작위로 선정된다. 예를 들어, 구명보트의 관측 방위각 3°의 신호 (σ_t=1.7×10^-3 m²)가 수신되는 경우는 식 (7)에 의해 SCR=-33.3 dB이다. 식 (6)과 식 (9)를 통해 크기 변환된 해상표적 신호를 해상클러터 신호에 결합하고, 해당 결합신호에 탐지기법을 적용한다.

표 3의 매개변수가 고려된 탐지기법들을 적용하여 각 기법의 성능을 도출했다. 각 기법의 탐지성능 비교를 위해서 Receiver Operating Characteristic(ROC) 커브(그림 12)를 계산하였다. 탐지율과 오경보율에 대한 정의는 다음 식 (20)과 같다.

P D = N det e c t N o p e r, P F = N d c N c

그림 12. | Fig. 12. 탐지성능비교를 위한 ROC 커브 | ROC curve of detection performance.

Download Original Figure

탐지율, P_D는 전체 반복 수행횟수, N_oper중에서 1개 이상의 표적 레인지 빈이 탐지된 수행 횟수, N_detect의 비율을 의미한다. 오경보율 P_F는 전체 클러터 레인지 빈 개수 N_dc중에서 탐지된 클러터 레인지 빈 개수 N_c의 비율이다.

그림 12의 ROC 커브는 다양한 문턱값 (CA-CFAR의 경우 P_FA)에서의 각 기법이 갖는 탐지율 및 오경보율을 나타내고 있다. 프랙탈, EMD, RBF-NN 기법이 CA-CFAR 기법보다 동일 오경보율에 대하여 낮은 탐지율을 지니며, 이것은 MFR 탐지모드에서 해당 탐지기법들이 CA-CFAR보다 저 RCS 해상표적탐지에 불리함을 의미한다.

프랙탈 기법을 이용하여 해상표적을 탐지하는 경우, 신호의 크기와 상관없이 프랙탈 특성에 의존하여 탐지를 수행하기 때문에 안정인 탐지 성능을 갖는다고 연구되어 왔다. 그러나 MFR 시스템의 탐지모드에서는 프랙탈 특성 추출에 필요한 시간축 신호가 부족하기 때문에, 프랙탈 차원에 대한 신호분석이 어렵다. 이로 인해 표적과 해상클러터간의 허스트 파라미터 값 차이가 작아져 탐지성능이 저하된다.

EMD 기법은 반복 단일함수 추출로 인해 실행시간이 길지만, 우수한 탐지성능을 기대할 수 있는 기법으로 알려져 있다. 그러나 MFR 탐지모드에서는 짧은 측정시간으로 인해 수신 데이터들의 크기 변화가 적고, 따라서, 단일함수 추출에 불리하다. 추세함수의 크기를 이용해서 탐지하는 EMD 기법의 특성상, 단일함수 추출이 제대로 수행되지 않는 MFR 탐지모드에서는 탐지기법의 탐지성능이 저하된다.

RBF-NN 탐지기법은 기존의 신경망회로를 이용한 탐지방법과 비교하여 빠른 학습시간과 일반화 능력이 우수하다. 이를 위해 다수의 뉴런을 포함한 신경망회로를 이용하여 혼돈상태의 해상클러터에 대한 비선형적 학습을 수행해야 한다. 그러나, 적은 수신 펄스 개수로 인해 입력뉴런의 개수가 적어 혼돈상황의 해상 클러터에 대해 사상함수 및 가중치에 대한 정확한 학습이 어렵고, 따라서 저하된 해상표적 탐지성능을 갖는다.

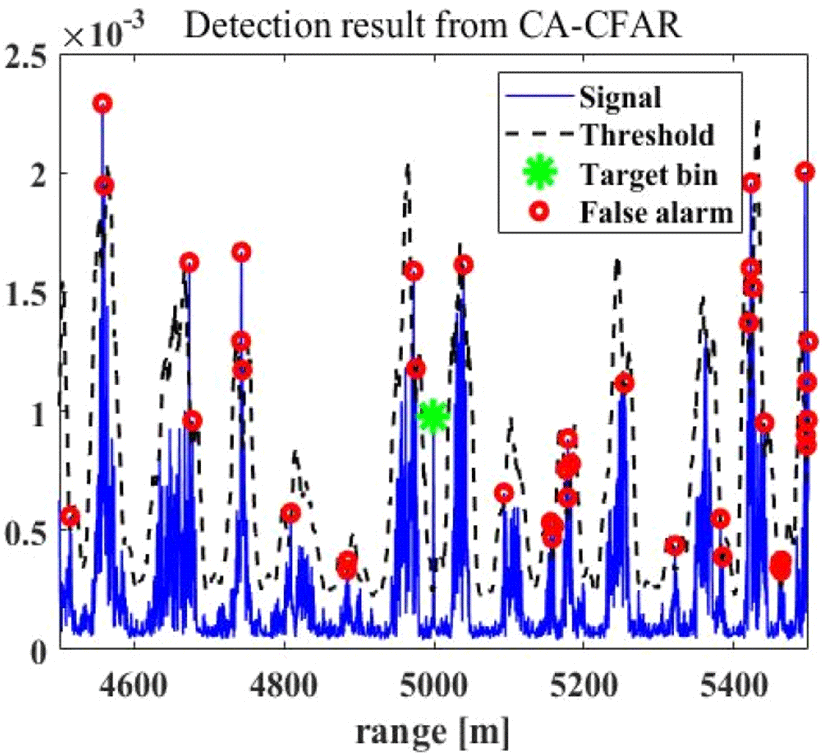
CA-CFAR 기법은 상기 기법들과 달리 거리축 해상 클러터 데이터에 대하여 탐지를 수행하는 기법으로 빠른 수행시간을 갖는다. 그러나, 표적의 신호가 주변 해상클러터보다 큰 경우에만 표적탐지가 가능하며, CA-CFAR 탐지기법의 특성상 연속적으로 분포된 레인지 빈에 존재하는 표적에 대해서는 탐지성능이 저하될 수 있다. 그림 12와 같이 CA-CFAR 탐지기법은 프랙탈, EMD, RBF-NN 탐지기법보다는 우수한 탐지성능을 갖지만, 일반적으로 그림 13처럼 해상표적 신호뿐만 아니라, 해상 스파이크 신호도 동시에 탐지된다. 탐지된 해상 스파이크 신호는 오경보이며, CA-CFAR 탐지기법을 저 RCS 해상표적 탐지에 사용하는 것은 여전히 많은 오경보를 발생시키므로 표적을 해상 스파이크로부터 변별할 수 있는 기능이 추가로 필요하다.

그림 13. | Fig. 13. P_FA=5×10^-2의 CA-CFAR로 인한 오경보 | False alarms from CA-CFAR with P_FA=5×10^-2.

Download Original Figure

Ⅵ. 결론 및 향후 연구 방향

본 논문에서는 MFR 시스템에서의 기존 해상표적 탐지기법 성능을 분석하기 위해 MFR 탐지모드에서 측정되는 해상클러터 모델링 방법을 제안 및 수행하고, 수치해석을 통해 획득한 표적신호와 결합하였다. 결합된 신호에 대해 기존 탐지기법의 탐지율과 오경보율을 ROC 커브를 통해 비교하였다. 프랙탈, EMD 및 RBF-NN 기법은 각각의 특성벡터를 추출하기 위해서 오랜 시간 측정된 데이터가 필요하기 때문에, 짧은 시간 동안에만 운용되는 MFR 탐지모드에는 부적합하다. CA-CFAR 탐지기법은 다른 탐지기법 대비 상대적으로 높은 탐지성능을 가지고 있지만, 여전히 많은 오경보가 발생하는 한계가 존재한다. 따라서, 이를 극복할 향후 탐지기법은 짧은 시간에도 구분되는 특징 벡터를 이용하여 표적과 해상 스파이크를 변별할 수 있어야 하며, 이를 통해 오경보율이 감소하도록 개발해야 한다.

Acknowledgement

본 연구를 위해 지원을 해주신 한화 시스템에 감사를 드립니다.

References

[1].

X. Chunsheng, C. Hao, and X. Dong, "Sea clutter characteristics analysis and target detection based on HHT," in 2011 International Conference on Consumer Electronics, Communications and Networks(CECNet), XianNing, Apr. 2011, pp. 694-697.

[2].

G. Hennessey, H. Leung, A. Drosopoulos, and P. C. Yip, "Sea-clutter modeling using a radial-basis-function neural network," IEEE Journal of Oceanic Engineering, vol. 26, no. 3, pp. 358-372, Jul. 2001.

[3].

J. Hu, W. W. Tung, and J. Gao, "Detection of low observable targets within sea clutter by structure function based multifractal analysis," IEEE Transaction on Antennas and Propagation, vol. 54, no. 1, pp. 136-143, Jan. 2006.

[4].

S. Miranda, C. Baker, K. Woodbridge, and H. Griffiths, "Knowledge-based resouce management for multifunciton radar: A look at scheduling and task prioritization," IEEE Signal Processing Magazine, vol. 23, no. 1, pp. 66-76, Feb. 2006.

[5].

I. Antipov, "Statistical analysis of Northern Australian coastline sea clutter data," Australian Government Department of Defence Science and Technology, DSTO-TR-1236, 2002.

[6].

X. Li, X. Xu, "A statistical model for correlated K-distributed sea clutter," in 2008 Congress on Image and Signal Processing, Sanya, Hainan, May 2008, pp. 408-412.

[7].

S. Watts, "Modeling and simulation of coherent sea clutter," IEEE Transactions on Aerospace and Electronic Systems, vol. 48, no. 4, pp. 3303-3317, Oct. 2012.

[8].

H. W. Melief, H. Greidanus, P. van Genderen, and P. Hoogeboom, "Analysis of sea spikes in radar sea clutter data," IEEE Transactions on Geoscience and Remote Sensing, vol. 44, no. 4, pp. 985-993, Apr. 2006

[9].

A. Farina, F. Ginin, M. V. Greco, and L. Verranzzani, "High resolution sea clutter data: Statistical analysis of recorded live data," in IEE Proceedings-Radar, Sonar and Navigation, Jun. 1997, vol. 144, no. 3, pp. 121-130.

[10].

S. H. Choi, J. M. Song, H. M. Jeon, Y. S. Chung, J. M. Kim, and S. W. Hong, et al., "Simulation of low-grazing-angle coherent sea clutter," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 8, pp. 615-623, Aug. 2018.

[11].

K. D. Ward, R. J. A. Tough, and S. Watts, Sea Clutter: Scattering, the K Distribution and Radar Performance, London, Institution of Engineering and Technology, 2006.

[12].

C. Ozdemir, Inverse Synthetic Aperture Radar Imaging with Matlab Algorithm, Mersin, John Wiley & Sons, 2012.

[13].

B. R. Mahafza, Radar Systems Analysis and Design Using Matlab, 2nd ed. New York, NY, CRC, 2005.

[14].

I. Antipov, "Simulation of sea clutter returns," Australian Government Department of Defence Science and Technology, DSTO-TR-0679, 1998.

[15].

M. A. Richards, Fundamentals of Radar Signal Processing, 2nd ed. Chicago, IL, McGraw-Hill, 2005.

[16].

Y. Yang, J. Deng, "Empirical mode decomposition as a tree-structured filter: A tutorial view," in 2010 International Conference on Biomedical Engineering and Computer Science, Wuhan, Apr. 2010, pp. 1-4.

[17].

L. Yujie, W. Wenguang, and S. Jinping, "Research of small target detection within sea clutter based on chaos," in 2009 International Conference on Environmental Science and Information Application Technology, Wuhan, Jul. 2009, pp. 469-472.

[18].

H. Leung, "Experimental modeling of electromagetic wave scattering from an ocean surface based on chaotic theory," Chaos, Solitons & Fractals, vol. 2, no. 1, pp. 25-43, Jan.-Feb. 1992.