The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2019; 30(6):487-497

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2019.30.6.487

논문/REGULAR PAPERS

비행 단계별 특성벡터 융합을 통한 효과적인 탄두 식별방법

최인오

, 김시호^*

, 정주호^**

, 김경태

, 박상홍^***^,^†

Efficient Recognition Method for Ballistic Warheads by the Fusion of Feature Vectors Based on Flight Phase

In-Oh Choi

, Si-Ho Kim^*

, Joo-Ho Jung^**

, Kyung-Tae Kim

, Sang-Hong Park^***^,^†

포항공과대학교 전자전기공학과

¹국방과학연구소

²포항공과대학교 기계공학과

³부경대학교 전자공학과

Department of Electrical Engineering, Pohang University of Science and Technology

¹3rd R&D Institute, Agency for Defence Development

²Department of Mechanical Engineering, Pohang University of Science and Technology

³Department of Electronic Engineering, Pukyong National University

^†Corresponding Author: Sang-Hong Park (e-mail: radar@pknu.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 09, 2019; Revised: Jun 08, 2019; Accepted: Jun 10, 2019

Published Online: Jun 30, 2019

요약

탄도미사일은 작은 레이다 단면적 및 빠른 기동 특성으로 인하여 탐지가 매우 힘들며, 또한 탄도미사일의 각 비행단계에서 탄두와 유사한 운동 변수로 기동하는 연료탱크 및 기만체의 존재로 인하여 탄두의 식별 및 요격이 매우 어렵다. 따라서 비행 단계에 따라 표적의 기동 및 미세운동을 이용한 특성벡터가 필요하며, 또한 이를 적절히 융합하여 비행 단계에 상관없이 식별하는 방법이 요구된다. 본 연구에서는 탄도미사일의 비행단계에 따른 유용한 특성벡터를 소개하고, 이를 특성벡터 및 구분기 레벨에서 융합하는 효과적인 기법을 제안한다. CAD 모델들을 사용하여 예측된 레이다 신호들로 시뮬레이션을 수행한 결과, 구분기 레벨 융합을 통하여 잡음환경 내에서 비행단계에 상관없이 종말 단계로 갈수록 보다 향상된 탄두 식별이 가능하였다.

Abstract

It is very difficult to detect ballistic missiles because of small cross-sections of the radar and the high maneuverability of the missiles. In addition, it is very difficult to recognize and intercept warheads because of the existence of debris and decoy with similar motion parameters in each flight phase. Therefore, feature vectors based on the maneuver, the micro-motion according to flight phase are needed, and the two types of features must be fused for the efficient recognition of ballistic warhead regardless of the flight phase. In this paper, we introduce feature vectors appropriate for each flight phase and an effective method to fuse them at the feature vector-level and classifier-level. According to the classification simulations using the radar signals predicted by the CAD models, the closer the warhead was to the final destination, the more improved was the classification performance. This was achieved by the classifier-level fusion, regardless of the flight phase in a noisy environment.

Keywords: Missile Recognition; Micro-Doppler; 3DFV; Ballistic Factor; Feature Fusion

Ⅰ. 서 론

제 2차 세계대전 기간에 독일에 의해서 탄도미사일 V1이 처음 사용된 이후, 이와 관련된 다양한 연구가 개발되어 왔다. 그 결과, 현재 다수의 국가에서 대륙간 탄도미사일을 보유하게 되었으며, 이는 각국의 국가 안보에 큰 위협이 되고 있다. 이를 해결하기 위하여 레이다를 사용한 탄도미사일의 사전 탐지 및 요격 연구가 최근까지 활발히 수행되어 왔다^[1]. 하지만, 그림 1(a)와 같이 탄도미사일에서 분리되는 연료 탱크(debris) 혹은 기만체(decoy)들은 탄도미사일의 탄두(warhead)에 대한 사전 탐지 및 요격을 방해하기 때문에 레이다를 통하여 탄두를 보다 정확하게 변별하기 위한 연구가 반드시 필요하다. 이때 연료 탱크와 기만체는 일반적으로 탄도미사일의 비행 단계에 따라 각각 다른 시점에서 분리되기 때문에 효과적인 변별을 위해서는 비행 단계마다 적합한 고유 특성들이 필요하다.

그림 1. | Fig. 1. 탄도미사일 구성요소 및 비행 단계 | Elements and flight stage of the ballistic missile.

Download Original Figure

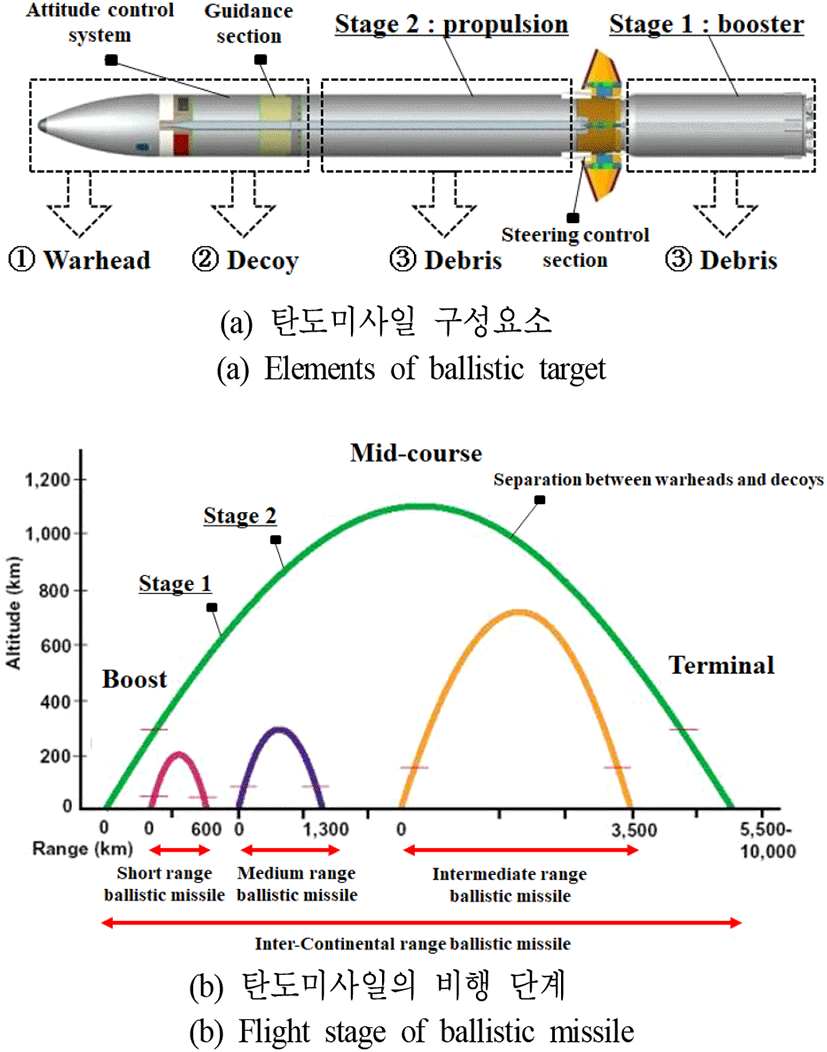
탄도미사일의 비행 단계는 크게 1) 추진(boost) 단계, 2) 중간(mid-course) 및 3) 종착(terminal) 단계로 구성된다^[2](그림 1(b)). 먼저 추진 단계는 탄도미사일 내 추진체의 연료 소모 및 발사각도 조절을 통한 상승 단계이다. 일반적으로 이 단계에서는 연료를 모두 소모하고, 1차 및 2차 분리되는 연료 탱크들이 탄도미사일의 사전 탐지를 방해하지만^[2], 이들의 속도 변화는 탄도미사일과 비교하여 빠르지 않기 때문에 거리(range)-시간(slow time) 영상 내 고해상도 거리측면도(high-resolution range profile: HRRP)들에서 나타나는 기동궤적을 통해 변별을 수행할 수 있다. 하지만 추진 단계 이후, 탄도미사일은 더 이상 추가적인 추진력 없이, 대기밀도가 매우 희박한 외기권 내에서 중력에 의하여 순항하는 중간 단계에 진입한다. 특히, 이 시점에서 탄도미사일은 레이다에 쉽게 노출되기 때문에 기만체들을 분리시켜 레이다를 기만시킨다^[2]^～^[6]. 이러한 기만체들은 보통 탄두와 유사한 형상을 가지기 때문에 대기밀도가 매우 희박한 외기권 내에서 탄두와 매우 유사한 기동 특성을 가진다^[4]. 따라서 중간 단계에서는 더 이상 HRRP들에서 나타나는 기동특성을 변별에 사용할 수 없기 때문에 탄두와 기만체간의 고유 미세운동(micro-motion) 차이로 인한 변별이 바람직하다^[5]^,^[6]. 마지막으로 종착 단계는 대기권 재진입 후, 중력과 더불어 항력의 영향으로 탄착지점까지 비행하는 단계이다. 이 시점에서는 대기밀도가 기하급수적으로 증가하기 때문에 항력가속도 차이에 의해 탄두와 기만체간의 기동궤적 차이가 크게 나타나며, 이를 효과적으로 추출할 경우 보다 효과적인 변별이 가능하다^[4]. 표 1은 탄두, 기만체 및 연료 탱크의 개별 특성들을 간략하게 보여준다.

표 1. | Table 1. 탄두, 기만체 및 연료 탱크의 특징 | Characteristics for warhead, decoy, and debris.

	Warhead	Decoy	Debris
Flight stage	Boost, mid-course, terminal	Mid-course, terminal	Boost
Maneuver	After boot-phase, they are in free-fall by both gravity and drag force
Micro-motion	Precession and nutation	Tumble or wobble	Wobble

Download Excel Table

본 논문에서는 기존에 저자들이 탄두와 기만체 간의 변별을 위하여 제안하였던 고유 특성벡터들(e.g. 기동기반 특성벡터^[2] 및 미세운동기반 특성벡터^[3])을 사용하여, 비행 단계에 상관없이 탄두를 효과적으로 변별하기 위한 새로운 시스템을 제안한다. 이때 제안된 시스템의 가장 큰 기여도는 고도에 따라 기동기반 특성벡터와 미세운동기반 특성벡터를 특성벡터 및 구분기 레벨에서 융합하여 비행 단계에 상관없이 높은 변별 성능을 달성한 것이다. 특히, 특성벡터 및 구분기 레벨에서의 융합 기법은 최근 다양한 레이다 분야에서 매우 활발히 사용되는 추세이다^[7]^,^[8]. 본 논문에서는 제안된 시스템의 성능 검증을 위하여 탄두 및 기만체의 computer-aided design(CAD) 모형들에 대한 물리광학(physical optics: PO) 및 물리회절학(physical theory of diffraction: PTD) 기반의 전자기 수치해석 데이터를 사용하였다. 이를 사용한 시뮬레이션 결과, 구분기 레벨 융합을 통해 비행단계에 상관없이 향상된 구분 성능을 달성할 수 있었다.

Ⅱ. 비행 단계별 특성벡터 추출 및 제안된 기법

Ⅱ장에서는 각 비행 단계에 따라 탄두를 효율적으로 변별하기 위해 필요한 특성벡터들의 소개 및 이를 활용한 새로운 변별 시스템에 대하여 서술한다.

2-1 추진 단계

서론에서 언급한 바와 같이, 추진 단계에서는 탄도미사일에서 1차 및 2차 분리되는 연료 탱크가 레이다를 통한 사전 탐지를 방해한다^[2]. 하지만, 탄도 미사일은 기존의 추진력을 통해 더 높은 고도로 올라가는 반면에 상대적으로 무거운 연료 탱크들은 떨림 운동과 함께 그대로 자유낙하 한다^[2]. 그 결과, 그림 2와 같이 분리 후에 HRRP들에서 나타나는 기동궤적을 이용하여 탄도미사일과 연료 탱크들 간의 간단한 변별이 가능하게 된다. 이때 HRRP는 처프 신호의 정합 필터링(matched-filtering)을 이용하여 얻을 수 있다^[9]. 만약 분리 전 시간 t=0～T 동안 HRRP들에서 사전 탐지된 탄도미사일의 기동궤적 r_traj(t)≈v_mt 이 일정한 속도 v_m 으로 변화한다고 가정할 경우, 분리 후 t= T～2T 동안의 탄도미사일 궤적 $r^t r a j (t) ≈ v^m t$ 는 간단한 선형 외삽(extrapolation)으로 속도 $v^m$ 을 추정하여 그림 2와 같이 예측할 수 있다. 이때 예측된 기동궤적 $r^t r a j (t)$ 를 사용하여 식 (1)과 같이 거리(range) 축에서 형성된 가 우시안 커널 g(r) 을 구성한 후, 실제 수신된 HRRP들에 적용하여 상대적으로 크게 벗어나는 연료탱크의 기동궤적을 제거한다(그림 2).

그림 2. | Fig. 2. 추진단계에서 탄도미사일과 연료탱크간의 변별 시나리오 | Discrimination scenario between ballistic missile and debris at boost phase.

Download Original Figure

g (r) = 1 2 π σ r 2 exp {− 1 2 σ r 2 (r − r^t r a j (t)) 2},

(1)

여기서 $σ r 2$ 는 탄도미사일의 궤적만 포함시키기 위한 거리 축에서의 분산이다.

2-2 중간 단계

탄도미사일은 고도 100 km 이상의 외기권에 진입한 후, 더 이상 추가적인 추진력이 없이 중력에 의해서만 낙하하는 중간 단계에 진입한다. 이때 레이다에 의한 사전 요격을 피하기 위해 탄두가 기만체와 함께 분리되며, 이 표적들은 공기 밀도가 매우 희박한 진공에 가까운 상태에서 기동하기 때문에 자유 낙하하는 기동궤적이 매우 유사하다^[4]. 따라서 중간단계에서는 탄두와 기만체간의 미세운동 차이를 이용하여 구분한다^[2]^,^[5]^,^[6]^,^[10]^,^[11].

중간 단계에서 원뿔 형상 탄두의 미세운동은 그림 3(a)에서 보는 바와 같이 기동궤적이 사전에 보상되고, z축을 기동방향이라고 가정할 경우, 회전운동(spinning), 원추운동(coning) 및 장동운동(nutation)으로 구성된다. 하지만, 이때 매끄러운 표면의 원뿔에서 나타나는 산란원들은 항 상 원뿔 바닥의 법선벡터와 레이다 시선방향벡터(radar line- of-sight: RLOS) $r → R L O S$ 가 이루는 평면에서 존재하기 때문에^[2], 회전운동은 존재하지 않는다. 이때 원추 및 장동운동은 로드리게스 회전공식으로 모델링이 가능하며^[5]^,^[6], 원뿔 형상 탄두에 대한 기저대역 continuous wave(CW) 기반의 레이다 수신신호는 다음과 같이 정의된다.

그림 3. | Fig. 3. 중간단계에서 탄두와 기만체간의 미세운동 | Micro-motion for warhead and decoy at mid-course phase.

Download Original Figure

s w (t) = ∑ m = 1 3 σ c o n (θ w) h m (t) × exp (j 4 π → T λ r w, m (t) ⋅ r → R L O S)

(2)

여기서 α_con (θ_a)는 원뿔 형상 탄두의 radar cross section (RCS), θ_w는 원추 및 장동운동에 의한 관측각도, h_m(t)는 m번째 effective 산란원의 가려짐 효과를 표현하기 위한 함수^[2], 그리고 $r → w, m (t)$ 는 원추 및 장동운동을 가지 는 m번째 산란점 P_m에 대한 실시간 위치벡터이다.

중간 단계에서 원뿔 기만체는 그림 2(b)와 같은 떨림 운동을 하며^[5]^,^[6], 원뿔 형상 기만체의 CW 레이다 수신신호는 다음과 같이 표현된다.

s d (t) = ∑ m = 1 3 σ c o n (θ m) p m (t) × exp (j 4 π → T λ r d, m (t) ⋅ r → R L O S),

(3)

여기서 θ_d는 떨림운동에 의한 관측각도, p_m(t)는 원뿔 형상 기만체에 대한 m번째 effective 산란원의 가려짐 효과를 표현하기 위한 함수^[2], 그리고 $r → d, m (t)$ 는 떨림운동을 가지는 m번째 산란점 P_m에 대한 실시간 위치벡터이다.

탄두와 기만체간의 미세운동의 차이점은 이들로부터 수신된 레이다 신호들(e.g. 식 (2) 및 식 (3)) 내 RCS 및 위상 차이를 야기한다. 본 논문에서는 이러한 차이를 효율적으 로 추출하기 위하여 최근 본 저자들에 의해서 제안된 3DFV(3-dimensional feature vector)^[5] $f → 3 D F V = [F 1, F 2, F 3] T$ 을 사용한다. 이 특성벡터를 추출하기 위해서는 레이다 수신신호에서 생성된 시간-주파수 영상 I_tf(t,f)을 주파수-주파수 영상 $I f f (f ′, f)$ 로 변환해야 한다^[5](그림 4). 이때 F₁은 $I f f (f ′, f)$ 의 1사분면에서 가장 큰 첫 번째 주 파수 성분이며, 미세운동의 주기성을 의미한다. F₂는 주파수가 0인 지점에서의 대역폭(bandwidth)을 나타내며, 미세운동에 의한 움직임 변화 폭울 의미한다. F₃는 본 저자들이 새롭게 정의한 다음 기저 함수를 이용하여 형성된다.

그림 4. | Fig. 4. 탄두와 기만체에 대한

I f f (f ′, f)

의 예시들^[5] | Examples of

I f f (f ′, f)

for warhead and decoy^[5].

Download Original Figure

b (t) = exp (F 2 j 2 π sin (2 π F 1 t)),

(4)

여기서 F₁ 및 F₂는 앞서 추출된 특징 값들이다. 식 (4)를 사용한 주파수-주파수 영역의 기저영상은 다음과 같다.

B (f ′, f) = | F t [T F [b (t)]] |,

(5)

여기서 F_t는 시간 t에서의 푸리에 변환이며, TF는 시간 영역의 신호 s_basis(t)에 대한 시간-주파수 영역으로의 변환이다. 최종적으로 F₃는 다음 식과 같이 정규화된 $I f f (f ′, f)$ 와 기저영상 $B (f ′, f)$ 의 투영으로 정의된다.

F 3 = ∑ f ′ ∑ f [B (f ′, f) ∑ f ′ ∑ f B (f ′, f) ⊗ I f f (f ′, f) ∑ f ′ ∑ f I f f (f ′, f)],

(6)

여기서 ⊗은 Hadamard 연산자이다. 여기서 주목할 점은 F₃를 추출할 때 탄두 고유 미세운동 특징을 나타내는 기 저영상 $B (f ′, f)$ 을 사용하기 때문에(그림 5), 기존 영상모멘트 추출기법들에 비하여 매우 적은 차원으로 높은 변별 특성을 획득할 수 있다^[5].

그림 5. | Fig. 5. F₃를 위한 기저영상

B (f ′, f)

^[5] | Basis image

B (f ′, f)

for F₃^[5].

Download Original Figure

2-3 종착 단계

대기권에 진입하는 종착 단계의 경우, 급격한 대기밀도 증가로 인해 탄두와 기만체간의 항력가속도 차이가 크게 발생하기 시작한다^[4]. 항력가속도 차이는 주로 표적의 물리적 특징인 질량 m, 표면적 S 및 항력계수 C_D로 인해 발생되며, 이때 이 3가지 변수들을 이용하여 탄도계수(ballistic factor) γ를 다음과 같이 정의할 수 있다^[4].

γ = C D S m = 2 a^D ρ (H^) v^m 2,

(7)

여기서 $a^D$ , $v^m$ 및 $H^$ 는 칼만필터(Kalman-Filter: KF)로 추정된 항력가속도, 속도 및 고도이며, $ρ (H^)$ 는 $H^$ 에서의 대기밀도이다^[4]. 탄두는 기만체에 비하여 상대적으로 무거운 물질들로 구성되기 때문에 탄두의 탄도계수는 기만체 보다 작은 값을 가지며, 이를 이용하여 탄두와 기만체를 효과적으로 구분할 수 있다(그림 6). 게다가 탄도계수 γ는 미세운동 특성에 기반한 특성벡터 3DFV $f → 3 D F V$ 와 독립적으로 기동 특성으로부터 추출 가능하기 때문에 이들 간의 융합을 통한 변별이 가능하다.

그림 6. | Fig. 6. 종착단계에서 탄도계수추정 알고리즘 및 예시^[4] | Algorithm and examples for ballistic factor estimation at terminal phase^[4].

Download Original Figure

2-4 제안된 융합 기법

추진 단계의 경우, HRRP에 나타나는 기동궤적 차이를 이용하여 비교적 쉽게 연료 탱크에 대한 구분이 가능하므로, 본 연구에서는 중간단계 및 종착단계에서 탄두와 기만체간의 보다 효율적인 변별을 위한 1) 특성벡터 융합 및 2) 구분기 융합 기법을 제안한다.

특성벡터 융합의 경우, 2-2에서 언급한 바와 같이 중간단계(e.g. H > 100 km)에서는 진공에 가까운 대기 특성으로 인하여 탄두 및 기만체가 유사한 기동궤적을 가지므로 미세운동 기반특성벡터 $f → 3 D F V = [F 1, F 2, F 3] T$ 가 적합하며, 종착 단계(e.g. H < 100 km)에서는 목적지에 근접 한 탄두로 인하여 빠른 변별과정이 필요하므로 식 (7)의 기동기반 특성 γ가 적합하다. 따라서 특성벡터 융합에서는 KF로 추정된 고도 $H^$ 에 따른 미세운동기반 특성벡터 가중치 $W m i c r o (H^)$ 와 기동기반 특성 가중치 $W m a c r o (H^)$ 를 이용하여 다음과 같은 새로운 4차원 특성벡터를 구성한다.

f → 4 D = [W m i c r o (H^) f → 3 D F V, W m a c r o (H^) γ] T,

(8)

여기서

W m i c r o (H^) = 0.2 tanh ((π 20) H^− 5 π) + 0.6,

(9)

W m i c r o (H^) = 0.2 tanh (− (π 20) H^+ 5 π) + 0.4.

(10)

그림 7은 고도 정보(e.g. 0 km < H < 200 km)에 따른 제안된 가중치 함수들의 변화를 보여준다. 최종적으로 식 (8)의 융합된 특성벡터는 간단한 nearest neighbor(NN) 구분기를 통해 구분된다.

그림 7. | Fig. 7. 제안된 가중치 함수들 | Proposed weight functions.

Download Original Figure

구분기 레벨의 융합은 특성벡터 융합의 경우와 같이 중간 및 종착단계에서 사용되는 특성벡터(i.e. $f → 3 D F V$ 및 γ)는 동일하지만, 특성벡터 융합과 달리 각 특성벡터 및 NN 구분기를 사용한 구분결과들을 융합한다. 이를 위하 여 특성벡터 $f → 3 D F V$ 와 γ를 사용한 구분결과들의 1×2 순위(ranking) 벡터를 각각 $R → m i c r o$ 와 $R → m a c r o$ 로 정의한다. 예를 들어, 특성벡터 $f → 3 D F V$ 를 사용하여 결정된 가장 높은 순위의 클래스가 탄두일 경우, $R → m a c r o = [1, 2] T$ 으로, 반면에 가장 높은 순위가 기만체일 경우, $R → m a c r o = [2, 1] T$ 이다. 마찬가지로 γ를 통한 순위벡터 $R → m a c r o$ 도 동일한 방식으로 정의되며, 이때 구분기 레벨 융합을 통해 재정의 되는 1×2순위 벡터의 i번째 값 $R → f u s i o n (i) (i = 1, 2)$ 는 식 (9) 및 (10)의 가중치 함수를 사용하여 다음과 같이 정의된다.

R → f u s i o n (i) = W m i c r o (H^) R → m i c r o (i) + W m a c r o (H^) R → m a c r o (i) .

(11)

최종적으로 식 (11)을 통해 정의된 1×2순위 벡터 $R → f u s i o n$ 에서 i=1번째가 가장 큰 값을 가질 경우(i.e. $R → f u s i o n (1) ≻ R → f u s i o n (2),$ ), 표적 클래스는 탄두로, 반면에 i=2번째가 가장 큰 값을 가질 경우, 기만체로 구분한다.

Ⅲ. 시뮬레이션 결과

Ⅲ장에서는 제안된 시스템의 성능 검증을 위하여 탄두와 기만체의 CAD 표적들(그림 8)과 PO + PTD 기반의 전자기 수치해석 도구를 사용하였다. 이때 탄두와 기만체의 기동특성에 의한 비행궤적 모델링^[4]을 위한 변수는 표 2 및 표 3과 같다. 게다가 이 표적들의 고유 미세운동 및 레 이다 수신신호 모델링^[5]^,^[6]을 위한 변수는 표 4와 같다.

그림 8. | Fig. 8. 탄두와 기만체의 CAD 모델들 | CAD models for warhead and decoy.

Download Original Figure

표 2. | Table 2. 탄두와 기만체의 규격^[4] | Specifications for warhead and decoy^[4].

	Cone-shaped warhead	Cone-shaped decoy	Cylinder-shaped decoy
Mass [kg]	700	200	400
Surface [m²]	0.6079	0.6079	0.6079
Drag coefficient	0.21	0.21	0.45
Height [m]	1	1	1
Diameter [m]	0.75	0.75	0.75

Download Excel Table

표 3. | Table 3. 기동 관련 실험 변수들^[4] | Simulation parameters for maneuver^[4].

Gravity acceleration [m²/s]	9.81
Radius of earth [km]	6.378
Initial angle of fire [deg.]	45
Total maneuvering time [sec]	421.75

Download Excel Table

표 4. | Table 4. 미세운동 관련 실험 변수들 | Simulation parameters for micro-motion.

Carrier frequency [GHz]	10
Observation time [sec]	0.5
Sampling frequency [kHz]	2
Wave length [m]	0.03
Aspect-angle [deg.]	−90～90
Coning frequency [Hz]	5, 6, 7
Coning angle [deg.]	6, 8, 10
Wobbling frequency [Hz]	5, 6, 7
Wobbling angle amplitude [deg.]	0～90
Polarization	HH

Download Excel Table

본 연구에서는 추진 단계에서 연료탱크에 대한 구분 성능 검증 실험을 3-1에서 먼저 수행한 후, 중간 및 종착단계에서 특성벡터 및 구분기 레벨 융합기법에 대한 성능 검증을 순차적으로 3-2에서 수행한다.

3-1 추진 단계

추진 단계에서 탄도미사일의 기동 궤적 모델링은 표 2 및 표 3의 조건으로 수행되었으며, 연료탱크의 경우는 원통 기만체의 조건으로 모델링되었다. 이때 각 레이다 수신신호는 중심주파수 10 GHz, 대역폭 100 MHz, 관측시간 1 sec 및 펄스반복주파수(pulse repetition frequency: PRF) 20 Hz의 조건으로 모델링되었으며, 그 결과 그림 9(a)와 같이 HRRP들을 획득할 수 있었다. 이때 분리 시점은 T= 0.5초로 가정하였으며, 그 결과 T=0.5～1초에서는 분리된 연료탱크에 의하여 정확한 탄도미사일 탐지가 어려움을 알 수 있었다. 이때 2-1에서 제안된 기법을 사용할 경우, 그림 9(b)와 같이 탄도미사일의 기동궤적만 정확히 탐지 할 수 있음을 확인할 수 있었다. 하지만, 식 (1)의 α_r값이 225 m까지 증가할 경우, 가우시안 커널이 연료탱크의 기동궤적까지 모두 포함하기 때문에 정확한 분리가 힘들었다(그림 9(c)). 따라서 α_r=225 m 이하의 값을 설정할 경우, 추진 단계에서 HRRP에 나타나는 기동궤적 차이를 이용하여 비교적 쉽게 연료 탱크에 대한 구분이 가능함을 확인할 수 있었다.

그림 9. | Fig. 9. 추진단계에서의 변별 결과 | Discrimination results at boost phase.

Download Original Figure

3-2 중간 및 종착 단계

중간 및 종착 단계에서는 추진 단계와 달리 학습데이터 기반의 식별 과정이 필요하다. 이때 잡음 환경에서 제안된 기법의 성능 검증을 수행하기 위하여 백색 가우시안 잡음을 신호 대 잡음비(signal-to-noise ratio: SNR)에 따라 시험데이터에 추가하였으며, 본 연구에서는 SNR=10, 20 dB의 조건에서 시뮬레이션을 수행하였다.

먼저 기동 특성의 학습데이터를 구성하기 위하여 탄두의 질량은 700, 710, …, 750 kg으로, 원뿔 기만체와 원통 기만체는 각각 100, 110, …, 150 kg 및 300, 310, …, 350 kg으로 설정하였다. 게다가 원뿔 기만체와 원통 기만체의 직경은 각각 0.88, 0.98, …, 1.38 m 및 1.28, 1.38, …, 1.78 m로, 이 표적들의 항력계수는 각각 0.21, 0.31, …, 0.71 및 0.45, 0.55, …, 0.95로 설정하였다. 반면에 시험데이터는 학습데이터를 구성하기 위한 변수 범위의 최대, 최소 값 사이에서 임의로 표적 당 50개씩 선택하여 구성된다.

다음으로 미세운동 특성의 학습데이터 구성 방법은 표 4와 같으며, 시험데이터는 표 4의 최대, 최소 값 사이에서 임의로 표적당 50개씩 선택하여 구성된다^[5].

탄두와 기만체 간의 변별 성능은 전체 시험데이터 개수와 정확히 클래스를 변별한 시험데이터 개수의 비(i.e. probability of correct classification: Pc)로 판단되며, 보다 신뢰성 있는 결과 분석을 위해 50번의 Monte Carlo 시뮬레이션을 통한 Pc들의 평균값을 성능 검증 도구로 사용하였다.

그림 10은 중간 및 종착단계(e.g. t=224.45～400초)에서 기동(maneuver), 미세운동(micro-motion), 특성벡터 융합(feature-level fusion) 및 구분기 융합(classifier-level fusion)에 따른 실시간 Pc들을 보여준다. 먼저 검은색 선의 탄도계수를 사용한 기동기반의 구분 성능은 종착단계(e.g. t=370～400초)에서 급격히 성능이 향상됨을 볼 수 있다. 이는 고도가 낮아짐에 따라 대기밀도가 증가하고, 그 결과 탄두와 기만체간의 항력가속도 차이가 증가하기 때문이다. 하지만 탄도계수는 잡음에 따른 KF의 성능에 매우 의존적이기 때문에 그림 10(b)와 같이 SNR이 감소할 경우, 변별 성능이 저하됨을 보였다. 반면에 빨간색선의 미세운동기반 특성은 전반적으로 Pc=80 % 부근에서 나타났다. 이러한 이유는 모든 관측각도에서 데이터베이스를 구성하여, 탄두와 기만체간의 유사한 일부 레이다 수신신호들이 존재하게 되고, 이 신호들이 미세운동기반의 변별 성능을 떨어뜨리기 때문이다. 하지만 파란색 선의 제안된 특성벡터 융합기법의 경우, 그림 10에서 보는 바와 같이 기동 및 미세운동 특성에 기반한 결과들보다 성능이 향상됨을 보였다. 게다가 초록색 선의 구분기 융합기법은 SNR= 10 및 20 dB 환경에서 고도 100 km 부근(e.g. t=360초)을 제외할 경우, 비행단계에 상관없이 매우 향상된 구분결과를 보여준다.

그림 10. | Fig. 10. 중간 및 종착 단계에서의 변별 결과. | Discrimination results at mid-course and terminal phase.

Download Original Figure

Ⅳ. 결 론

본 논문에서는 비행단계에 상관없이 탄두의 높은 식별 성능을 달성하기 위한 새로운 시스템을 제안하였다. 이를 위하여 아래와 같이 각 비행단계별로 최적의 특성벡터들을 사용하였으며, 고도에 따른 새로운 융합 기법을 개발하였다.

1) 추진 단계: HRRP들에 나타나는 기동궤적의 차이를 바탕으로 탄도미사일과 연료탱크들의 분리 수행

2) 중간 및 종착 단계: 고도에 따른 새로운 가중치 함수들을 구성하여 기동 및 미세운동기반의 특성벡터들에 대한 특성벡터 및 구분기 레벨 융합 수행

CAD 모델 및 전자기 수치해석 도구를 사용한 시뮬레이션 결과, 제안된 구분기 레벨 융합을 수행할 경우, 비행단계에 상관없이 향상된 구분성능을 달성할 수 있었다.

Acknowledgements

「본 연구는 방위사업청과 국방과학연구소가 지원하는 레이다/IR 표적식별 특화연구실 사업의 일환 및 2018년도 정부(교육과학기술부)의 재원으로 한국연구재단의 기초연구사업(2018R1D1A1B07044981) 지원을 받아 수행되었습니다.」

References

[1].

G. N. Lewis, T. A. Postol, "Future challenges to ballistic missile defence," IEEE Spectrum, vol. 34, no. 9, pp. 60-68, Sep. 1997.

[2].

A. R. Persico, C. Clemente, D. Gaglione, C. V. Ilioudis, J. Cao, and L. Pallotta, et al., "On model, algorithms, and experiment for micro-Doppler-based recognition of ballistic targets," IEEE Transactions on Aerosapce and Electronic Systems, vol. 53, no. 3, pp. 1088-1108, Jun. 2017.

[3].

Y. J. Choi, I. S. Choi, J. Shin, and M. Chung, "Classification of the front body of a missile and debris in boosting part separation phase using periodic and statistical properties of dynamics RCS," Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 7, pp. 540-549, Jul. 2018.

[4].

I. O. Choi, K. B. Kang, S. H. Kim, J. H. Jung, K. T. Kim, and S. H. Park, "Performance analysis of the discrimination between space-targets using the maneuvering," Journal of Korean Institute of Information Technology, vol. 15, no. 11, pp. 55-63, Nov. 2017.

[5].

I. O. Choi, J. H. Jung, K. T. Kim, L. Riggs, S. H. Kim, and S. H. Park, "Efficient 3DFV for improved discrimination of ballistic warhead," Electronics Letters, vol. 54, no. 25, pp. 1452-1454, Dec. 2018.

[6].

I. O Choi, S. H. Kim, J. H. Jung, K. T. Kim, and S. H. Park, "An efficient method to extract the micro-motion parameter of the missile using the time-frequency image," Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 27, no. 6, pp. 557-565, Jun. 2016.

[7].

C. Guo, H. Wang, T. Jian, Y. He, and X. Zhang, "Radar target recognition based on feature Pyramid fusion lightweight CNN," IEEE Access, vol. 7, pp. 51140-51149, Apr. 2019.

[8].

Y. J. Choi, I. S. Choi, and D. Y. Chae, "Decision-level fusion scheme of SVM and naive Bayes classifier for radar target recognition," in 2018 International Symposium on Antennas and Propagation(ISAP), Busan, Oct. 2018, pp. 1-2.

[9].

S. H. Kim, S. I. Lee, and D. Y. Chae, "Aircraft classification with fusion of HRRP and JEM based on the confidence of a classifier," Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 28, no. 3, pp. 217-224, Mar. 2017.

[10].

H. Gao, L. Xie, S. Wen, and Y. Kuang, "Micro-Doppler signature extraction from ballistic target with micro-motions," IEEE Transactions on Aerospace and Electronic Systems, vol. 46, no. 4, pp. 1969-1982, Oct. 2010.

[11].

L. Liu, D. McLernon, M. Ghogho, W. Hu, and J. Huang, "Ballistic missile detection via micro-Doppler frequency estimation from radar return," Digital Signal Processing, vol. 22, no. 1, pp. 87-95, Jan. 2012.