Ⅰ. 서 론
항공기용 레이다는 항공기의 전 방향에서 접근 및 퇴각하는 표적을 탐지/추적하기 위하여 MPRF(Medium Pulse Repetition Frequency) 파형을 사용한다[1],[5]. MPRF 파형은 전 방향의 표적을 탐지할 수 있는 이점은 있지만, 클러터 환경에 취약하며, 낮은 항공기 고도 등의 상황에서 표적 탐지거리가 현저히 줄어든다[2]. HPRF(High Pulse Repetition Frequency) 파형은 MPRF 파형처럼 전 방위의 표적에 대해 고른 탐지능력을 가지는 것은 아니지만, 낮은 항공기 고도 등의 상황에서도 클러터 제약을 받지 않고, 전방의 먼 거리에서 빠르게 접근하는 표적을 속도의 모호성이 없이 탐지할 수 있다[1],[5]. 그래서 항공기 레이다에서는 먼 거리에서 전방으로 빠르게 접근하는 표적을 신속하게 탐지/추적하기 위한 모드를 운용하기 위하여 HPRF 파형을 사용하기도 한다. 그러나 HPRF 파형은 거리 방향으로 모호성이 극심하여 표적의 거리를 추출하기 힘들며, 보통 탐지된 표적의 속도 정보만을 사용해야 하는 단점이 있다[1]. 먼 거리에서 HPRF 파형으로 탐지된 표적에 대해 표적의 거리 정보를 이용한 표적 추적을 형성하기 위해서는 충분히 적은 오차로 표적 거리 정보를 추출할 수 있어야 하지만, 알려진 FM(Frequency Modulation) ranging 방법 등의 거리 추출 방법은 거리 측정값의 불확실성이 수 km까지 달한다[1]. 그러므로 HPRF 파형으로 표적을 탐지/추적하기 위해서는 표적 추적을 형성할 만한 적은 오차로 거리를 추출하는 방법을 고안해야 한다. 그리고 더불어 원하는 거리 및 속도 영역에서 표적을 최적으로 탐지/추적할 수 있는 HPRF 운용 파형 및 신호처리, 그리고 추적 파형 운용 설계 등이 이루어져야 한다.
본 연구에서 설계한 AESA(Active Electronically Scanned Array) 레이다는 아주 짧은 펄스 단위로는 전자식 빔 조향을 하지 않고 펄스 단위보다는 비교적 긴 시간 단위인 버스트(burst) 단위로 전자식 빔 조향 제어를 한다. 그리고 전자식 빔 조향이므로 어느 방향에서든지 즉각적인 빔 조향이 가능하다. 이러한 AESA 레이다의 빔 운용 특징을 고려하여, 본 논문에서는 AESA 레이다를 이용한 전방 고속표적 탐지에 적합한 HPRF 파형운용과 표적 탐지/추적 처리 흐름, 그리고 처리 단계별 신호처리 알고리즘을 제시한다.
본 논문에서 제시한 방법으로 비행 시험을 통해 획득한 시험 결과를 제시한다. AESA 레이다를 수송기(cargo aircraft)의 램프도어에 설치하고, 램프도어 개방 상태에서 후방으로 송신 신호 방사하여 시험을 하였다. 표적기로서 전투기가 사용되었다. 이런 수송기 탑재 비행 시험이라는 특수한 상황에서도, AESA 레이다를 이용한 비행시험을 통해 HPRF 파형을 사용하여 구현한 전방 고속표적 탐지/추적 모드의 기능이 잘 동작함을 확인하였다.
Ⅱ. HPRF 파형과 표적탐지
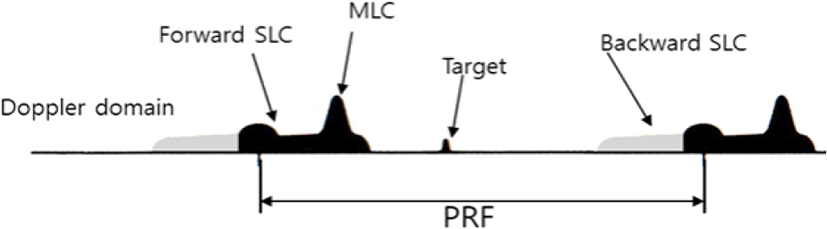
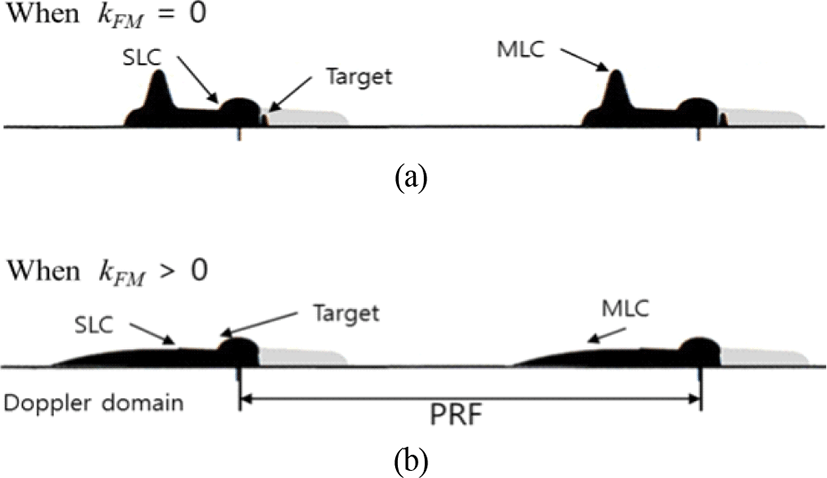
HPRF 파형은 표적의 관심 도플러 속도 영역이 모호성 없이 탐지 및 추출이 되도록 하는 PRF(Pulse Repetition Frequency) 범위를 사용하는 파형이다. 만약 관심 도플러 속도가 10 m/s에서 1,000 m/s 범위라고 한다면, 운용할 PRF의 값은 (2×1000/λ) 이상의 값이어야 한다. 여기서 λ는 송신파장을 나타낸다. 그리고 전방에서 빠르게 접근하는 표적을 클러터가 완전히 존재하지 않는 도플러 영역에서 탐지할 수 있도록 하기 위해서는 PRF를 관심 도플러 속도 최대치와 플랫폼 속도를 더한 도플러 값 이상이 되도록 해야 한다. 이는 부엽클러터 등을 완전히 배제한 도플러 영역에서 접근하는 표적을 탐지하기 위함이다. 즉, PRF > (2×1000+vp)/λ이다. 그림 1은 도플러 영역에서 HPRF 파형의 PRF 값과 표적 및 MLC(주엽클러터, Main Lobe Clutter), SLC(부엽클러터, Side Lobe Clutter)의 위치 관계를 표현한 것이다. 그림 1에서 Forward SLC는 안테나 전방 방향에서 안테나 부엽으로 들어오는 부엽클러터를 나타내고, Backward SLC는 안테나 후방 방향에서 안테나 부엽으로 들어오는 부엽클러터를 나타낸다. 보통 안테나 후방 방향에서 들어오는 부엽클러터의 전력은 아주 작아서 클러터 영향을 무시할 수 있으며, 그림 1에서 연한 회색으로 표현하였다. 플랫폼의 속도가 높을수록 그림 1 에서 부엽클러터 영역이 넓어진다. 그러므로 고정된 PRF 값으로 HPRF 파형을 운영한다면 플랫폼 속도의 최대치를 고려하여 PRF 값을 선정하여야 할 것이다.
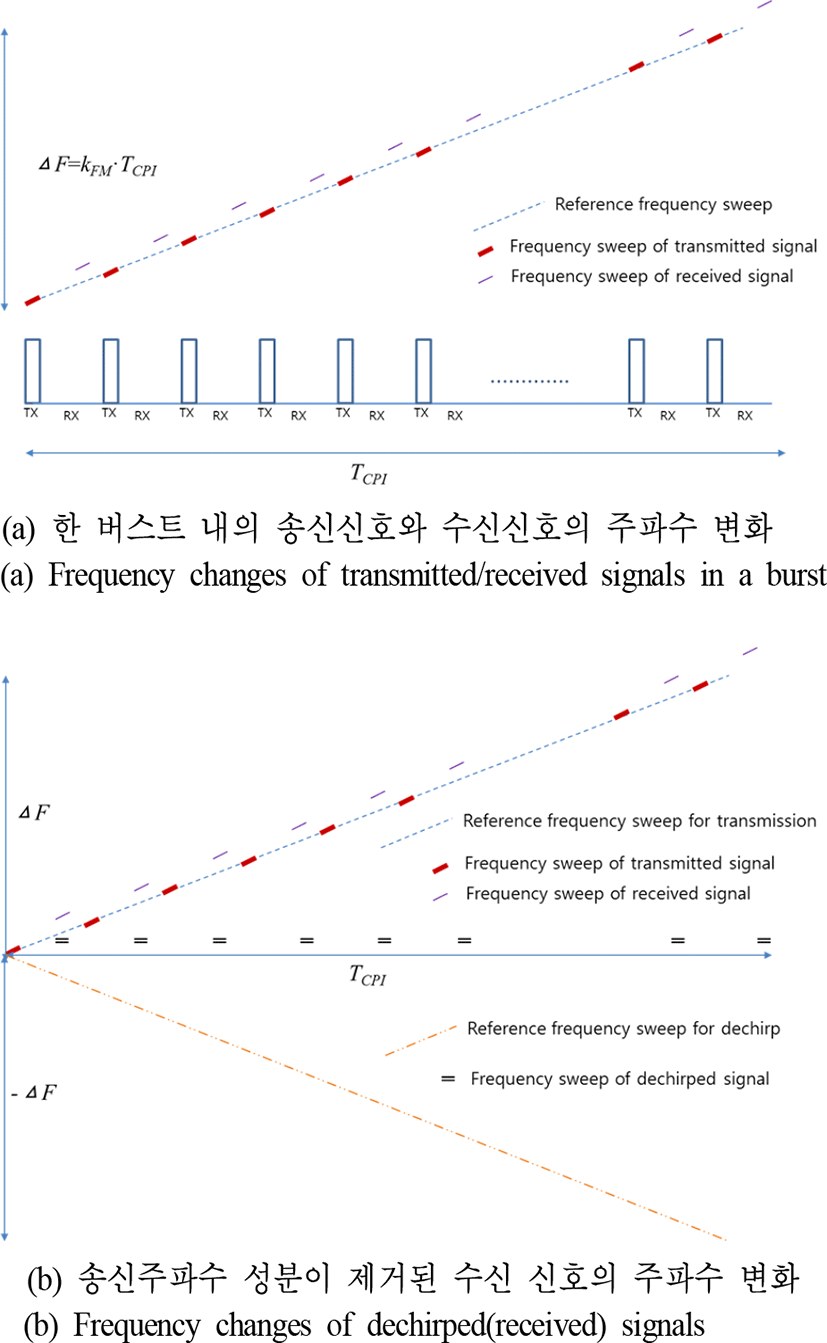
HPRF 파형의 탐색(search) 빔으로 스캔하면서 표적을 최초 탐지한 이후 지속적으로 해당 표적을 탐지하기 위한 추적을 형성하기 위해서는 표적 최초 탐지 이후에 빠르게 다시 표적이 탐지되었던 방향으로 표적을 확인(confirm)하는 빔을 운용하여야 한다. 본 논문의 HPRF 파형의 탐색 빔은 하나의 버스트로 되며, 탐색 빔 만으로는 표적 방향으로의 표적의 속도만 알 수 있고 모호성 없는 실제 거리는 알 수 없다. 그래서 다음 몇 초 후에(비교적 긴 시간 이후에) 표적의 위치를 예상할 수 없고, 빠른 속도의 표적이 파형의 블라인드(blind) 영역에 들어가서 표적을 탐지 못할 가능성이 커지므로 표적의 방향 위치와 속도가 변하기 전에 가능한 빠르게 다시 표적이 탐지되었던 방향으로 표적을 확인하는 과정이 필요하다. 표적을 확인하는 빔은 표적을 탐색하는 빔과 같은 PRF를 가지는 HPRF 파형을 사용할 수 있으며, 표적의 거리 추적을 형성하기 위해서 표적 거리를 추출할 수 있어야 한다. 최초 표적 탐지이후 빠른 확인 빔 운용이 가능하도록 하려면 빠른 신호처리 시간을 요구하므로 빠른 처리 및 응답 속도를 위한 신호처리 구현 설계가 필요하다. 본 논문에서는 확인 빔에서 FM ranging 기법을 이용하여 표적 거리를 추출[1]한다. 그리고 FM ranging 기법으로 추출한 표적 거리의 오차를 줄이고, 표적 추적이 형성할 수 있을 정도로 더 작은 오차의 표적 거리를 추출하는 추가적인 후처리를 한다[3]. FM ranging 기법은 3개의 버스트(burst)를 운영하여 표적 거리를 추출하는데, 버스트별로 서로 다른 비율로 송신주파수를 선형적으로 변화시켜서 각 버스트에서 레이다 반사 신호를 획득한다[1]. 각 버스트에서 획득한 레이다 반사파 신호에서 각 버스트의 송신주파수 성분을 제거하고 획득되는 표적의 비트(beat) 주파수들을 이용하여 모호성 없는 표적의 거리를 추출한다. 그림 2(a)는 FM ranging을 위한 한 버스트 송신할 때의 송/수신 신호의 주파수 변화를 나타낸다. 그림 2(a)에서 가로 축은 시간축이며, TCPI는 한 버스트 시간을 나타낸다. 그리고 세로축은 주파수축이며, kFM은 단위시간 당 주파수 변화율을 나타낸다. 그러므로 kFMTCPI는 한 버스트 시간에서 송신주 파수의 변화량을 나타낸다. 그림 2(a)에서 보듯이 펄스 송신 주기에 시간에 따라 kFM의 비율로 주파수가 증가하는 기준신호(reference of frequency sweep)에 따라 송신신호를 생성한다. 즉, 송신신호도 기준신호의 주파수 변화(frequency sweep of transmitted signal)를 따라가면서 전송된다. 레이다 수신신호는 송신신호를 반사한 물체의 거리에 따라 송신신호가 지연된 형태로 수신된다. 수신신호는 송신신호와 같은 주파수 변화(frequency sweep of received signal)를 보이지만, 단지 시간적으로 지연된 신호이다. 즉, 기준신호와 수신신호의 주파수 차이가 지연시간과 관련이 있음을 알 수 있다. 그림 2(b)는 수신신호에서 송신 때 들어간 시간에 따라 변하는 주파수 성분을 제거(dechirp)하기 위해 기준신호의 주파수 변화의 음의 방향으로 주파수가 변하는(reference frequency sweep for dechirp) 신호를 사용한 결과를 보여준다. 수신신호와 기준신호의 주파수 변화의 음의 방향으로 주파수가 변하는 신호를 곱하여 송신 때 주파수 변화 성분이 제거된(frequency sweep for dechirped signal) 신호를 얻는다. 이 신호에는 표적의 거리에 따른 시간 지연 정보와 표적의 도플러 정보가 섞여서 들어 있다. 이 신호를 도플러 처리하여 획득한 표적의 비트 주파수는 fd−kFMtr의 값을 가진다. 여기서 f_d는 표적의 도플러를 나타내고, tr은 표적의 거리에 의한 송신과 레이다 반사 수신신호 사이의 시간지연으로 C×tr/2는 표적 거리를 나타내게 된다(C는 광속도). 서로 다르게 주파수가 변하는 3개의 버스트를 운용하고, 3개의 버스트에서의 정보를 조합하여 고스트 등의 문제를 감소시켜 표적의 거리를 추출한다. 참고문헌 [1]에서도 언급하였듯이 송신주파수가 감소하는 방향으로 주파수를 선형적으로 변화시키면서 비트 주파수를 획득하면 클러터 영역이 표적을 탐지하는 영역까지 확장되어 표적 탐지를 방해할 수 있다. 그림 3은 표적의 비트 주파수를 획득하기 위해서 송신주파수를 감소하는 방향과 증가하는 방향으로 선형적으로 변화시켰을 때 클러터가 확장되는 영역을 비교 설명한 그림이다. 그림 3(a)는 송신주파수를 변화시키지 않고 일정하게 한 경우이며, 송신주파수 성분을 제거하고 기저대역으로 레이다 반사 신호 성분들을 이동시키면, 표적을 탐색하는 버스트 빔과 같은 형태로 클러터와 표적 분포를 보인다. 그림 3(b)는 송신주파수가 한 버스트 빔을 송신하는 동안 음수인 kFM 값의 비율로 선형적으로 변하는 경우이며, 송신주파수 성분을 송신주파수와 반대 방향의 비율로 변하는 신호를 이용하여 제거하고, 기저대역으로 레이다 반사 신호 성분들을 이동시키면, 클러터 반사체의 거리 값에 비례하여 클러터가 도플러 영역에서 양의 방향으로 이동하여 번져나가게 되어 원래 클러터가 없던 깨끗한 영역에 까지 클러터가 확장되어 존재하게 된다. 즉, 그림 3(b)에서 보듯이 클러터가 표적을 가려서 탐지를 어렵게 할 가능성이 커진다. 참고로 표적도 표적 거리에 비례하여 도플러 영역에서 양의 방향으로 이동하여 위치하고 있다. 그림 3(c)는 송신주파수가 한 버스트 빔을 송신하는 동안 양수인 kFM 값의 비율로 선형적으로 변하는 경우이며, 송신주파수 성분을 송신주파수와 반대 방향의 비율로 변하는 신호를 이용하여 제거하고, 기저대역으로 레이다 반사 신호 성분들을 이동시키면, 클러터 반사체의 거리 값에 비례하여 클러터가 도플러 영역에서 음의 방향으로 이동하여 번져나가게 된다. 그림 3(c)는 그림 3(b)와는 달리 접근하는 표적이 존재하는 도플러 영역이 클러터가 없는 깨끗한 영역으로 유지되고 있음을 볼 수 있다. 즉, 빠르게 접근하는 표적을 탐지한다는 목적에 부합하여 표적을 탐지할 수 있다. 참고로 표적도 표적 거리에 비례하여 도플러 영역에서 음의 방향으로 이동하여 위치하고 있다. 그림 3에서 알 수 있듯이 FM ranging을 이용해 빠르게 접근하는 표적을 탐지 및 거리 값을 추출하기 위해서 송신주파수가 증가하는 방향으로 주파수를 선형적으로 변화시키면서 운용하도록 하는 것이 유리하고, 본 논문의 표적 확인 빔에서는 송신주파수가 선형적으로 증가하도록 하여 운영한다. 확인 빔에서 FM ranging으로 추출한 측정오차(Δte)는 Δte= DBW3dB/kFM이다[1]. 여기서 DBW3dB 는 도플러 처리 후 도플러 해상도(resolution)을 나타내는 것으로 DBW3dB=PRF/NFFT이다. NFFT는 도플러 필터의 개수를 나타낸다. HPRF 파형의 PRF 및 NFFT로 Δte에 따른 거리 측정오차(Δte×C/2)는 수백 m에서 수 km에 이른다. 이런 거리 추출 정확도로는 추적 필터에서 표적 추적을 형성하기 어렵다. 참고문헌 [3]은 디지털 샘플링 해상도 정도의 오차로 표적 거리 값을 추출하는 방법을 제시한다. 본 논문은 참고문헌 [3]의 방법을 활용하여 표적 거리 추출 정확도를 높였다. 참고문헌 [3]의 방법이 제대로 동작하기 위해서는 Δte < PRI/2이라는 조건이 만족해야 하며(여기서, PRI=1/PRF), 이 조건과 앞에서 설명한 PRF 범위 조건 등을 반영하면 PRF는 다음과 같은 조건을 만족해야 한다.

여기서 vtm는 관심 표적의 최대 속도, vpm는 플랫폼의 최대속도이다. 식 (1)을 만족하는 PRF가 존재하려면 표적의 최소 탐지 속도 등을 고려하여 적절한 kFM을 선정해야 한다. NFFT는 표적의 탐지 거리에 의해 결정되는 버스트 시간에 의해 결정된다. 본 논문에서 제시한 표적 확인 빔에서 표적 거리를 추출하는 방법은 다음 장에서 더 자세히 설명한다.
표적 확인 빔에서 표적이 확인되고, 표적의 거리를 추출하여 추적 형성이 시작되었다면(추적이 형성되려면 몇 번의 확인 빔을 운영하여 몇 번의 표적 거리가 추출되어야 한다), 표적 추적에 특화된 추적 빔을 사용할 수 있다. 표적 추적이 시작되면 표적의 거리 및 속도를 예상할 수 있으므로, 예상되는 표적이 깨끗하게 탐지될 수 있도록 최적의 PRF를 선택하고, 예상되는 거리의 표적이 충분한 수신 전력으로 탐지될 수 있도록 버스트 시간을 선정할 수 있다. 본 논문에서는 단일 버스트 빔을 이용하는 추적 빔을 운용하고, 참고문헌 [2]에 제시한 방법으로 PRF를 선택하였으며, 표적 거리 별로 빔의 버스트 시간을 미리 선정한 값으로 사용하였다.
Ⅲ. 전방 고속표적 탐지/추적 단계 및 알고리즘 설계
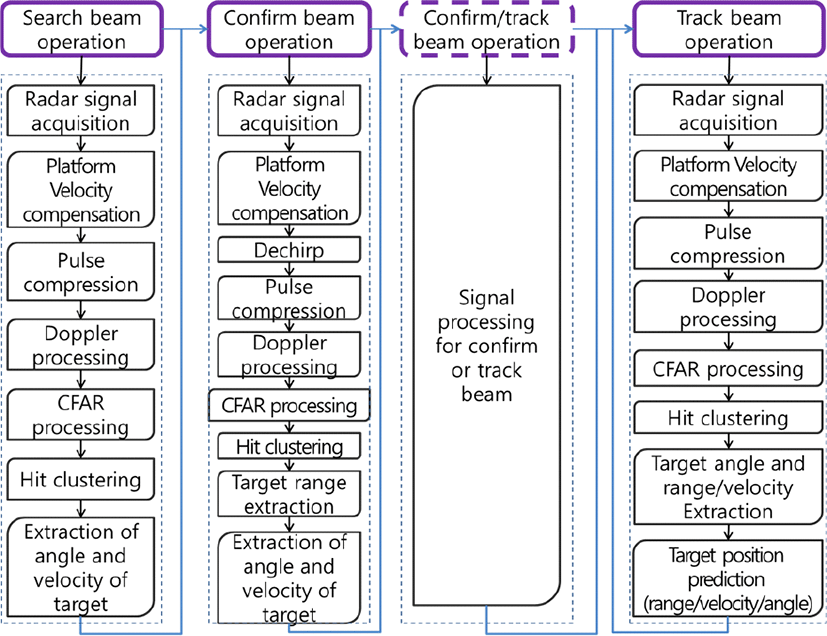
이 장에서는 AESA 레이다를 이용한 전방 고속표적 탐지/추적 모드의 표적 탐지/추적 처리 흐름을 제시하고, 각 단계의 기능 및 신호처리 알고리즘 설계를 기술한다. 그림 4는 전방 고속표적 탐지/추적 처리 흐름이다. 그림 4의 상단은 빔 운용을 나타낸다. 그림 4의 상단에서 확인 또는 추적 빔 운용 부분을 점선으로 표기한 것은 해당 단계에서 빔 운용은 확인 빔 또는 추적 빔을 선택 또는 혼용해서 사용할 수 있음을 표현한 것이다.
그림 4에서 표적 탐색 빔에 대한 신호처리 흐름을 그림 상단의 탐색 빔 운용 아래로 표현하였다. 탐색 빔을 운영하여 레이다 반사 신호를 획득하고, 레이다 반사 신호에서 플랫폼 속도를 보상한다. 플랫폼 속도 보상은 레이다 반사 신호에서 플랫폼 속도에 의한 도플러 성분을 없애는 것으로, 각 버스트에 대해서 안테나 빔 중심 방향(빔 조향 방향)에 대한 플랫폼의 속도 성분에 의한 도플러가 제로(zero)가 되도록 보상하는 것이다. 이것은 플랫폼 속도에 의한 도플러에 해당하는 매 펄스마다의 위상변화량을 레이다 획득 신호의 매 펄스마다 빼줌으로써 구현된다. 플랫폼 속도 보상 처리의 목적은 레이다 반사 신호에서 빔 조향 방향으로의 표적의 절대 속도를 획득하여 처리하기 위해서이다. 펄스 압축은 경사 거리 해상도를 높이기 위함이다[4]. 도플러 처리는 버스트 단위로 행하는 것이며, 펄스들의 동일 거리 셀의 샘플링 데이터들에 대하여 FFT(Fast Fourier Transform) 처리를 함으로써 구현된다[4]. CFAR(Constant False Alarm Rate) 처리 및 Hit 클러스터링 처리로 거리/도플러 맵에서 표적의 탐지 위치(Hit)를 추출한다. 표적 방향각 및 속도 추출은 추출된 표적 위치(Hit)들에 대해 빔 조향각 정보 및 모노펄스 처리를 통해 표적 방향각(표적의 고각 및 방위각)을 추출하고, 표적 Hit의 도플러 정보를 이용해 모호성 없는 표적 속도 값을 추출한다. 이렇게 표적 탐색 빔에서 추출한 표적 정보를 이용해서 표적 확인 빔을 생성하고 운용한다.
그림 4에서 표적 확인 빔에 대한 신호처리 흐름을 그림 상단의 확인 빔 운용 아래에 표현하였다. 레이다 신호 획득 및 플랫폼 속도 보상은 탐색 빔에서의 과정과 같은 처리 과정이다. 본 논문은 FM ranging 기법을 이용한 표적 거리 추출을 위하여 다음과 같은 3가지의 각기 다른 chirp을 기준신호로 하여 송신 신호를 형성한 3개의 버스트로 구성된 확인 빔을 운용한다.
여기서 t는 시간(second) 변수, fc는 주파수 상수 값, 그리고 kFM1, kFM2, kFM3은 (n+1)kFM1=nkFM2 및 kFM3=0의 관계를 가지는 상수 값이며, n 은 양의 정수, kFM1과 kFM2는 모두 양의 실수 값이다. Dechirp은 그림 2에서 설명하였듯이 송신 때에 사용된 시간에 따라 변하는 송신 주파수 변화의 음의 방향으로 주파수가 변하는 신호를 수신신호에 곱하여 송신 때 송신 주파수 변화 성분을 제거하는 과정이다. 펄스 압축, 도플러 처리, CFAR 처리, 그리고 Hit 클러스터링 과정은 탐색 빔에서의 처리와 동일한 처리를 하는 과정이다. 표적 거리 추출은 2장에서 설명한 FM ranging 기법을 이용한 표적 거리 추출과 그 추출한 거리 값의 오차를 줄이는 추가적인 후처리 과정이다. 식 (2)의 마지막 행의 기준신호로 운영한 버스트에 대해서 추출한 표적의 비트 주파수는 표적의 도플러 주파수 fd를 나타낸다. 그리고 식 (2)의 첫 번째와 두 번째 행의 기준신호로 운영한 각 버스트에 대해서 추출한 표적의 비트 주파수 fb1과 fb2는 각각 fb1=fd−kFM1tr 및 fb2=fd−kFM2tr과 같은 관계식을 가진다(tr은 표적 거리에 의한 송신과 수신 사이의 시간지연). 그러므로 하나의 표적에 대해 확인 빔의 각 버스트에 추출한 비트 주파수들은 다음과 같은 식을 만족한다.
식 (3)의 관계식을 만족하는 각 버스트의 표적 Hit를 하나씩 가지는 트리오(trio)들을 ((n+1) fb1−nfb2−fd)의 값을 이용해 찾아보자. (((n+1) fb1−nfb2−fd)≺Cws)의 조건을 만족하는 트리오들을 찾는다면, 이런 트리오들은 오표적 및 고스트 표적이 아닌 실제 표적이 형성한 트리오가 될 것이다. 즉, 오표적 및 고스트 표적을 배제한 실제 표적의 모호성 없는 거리를 추출할 수 있을 것이다. 여기서 Cws는 도플러 측정오차 및 표적의 움직임 등을 고려하여 도플러 해상도의 2에서 4배 정도의 값으로 설정할 수 있을 것이다. Cws의 값이 작으면 오표적 및 고스트 표적을 배제하는 효과가 커질 것이지만, 실 표적을 배제할 가능성도 커질 것이다. Cws의 값이 크면 오표적 및 고스트 표적을 추출할 가능성이 커지지만 실 표적도 놓치지 않고 추출할 가능성이 커진다. 그러므로 적절한 Cws의 값 설정이 필요하다. 표적 거리를 나타내는 시간지연은 식 tr=(fd−fb1)/kFM1을 이용하여 계산한다. 본 논문의 연구에서 구현한 확인 빔에서 FM ranging 기법에 기반한 표적의 시간지연(표적 거리)을 추출하는 처리 과정을 부록에 자세히 설명하였다. 앞에서 언급했듯이 이렇게 계산한 표적의 시간지연은 오차가 크다. 그래서 참고문헌 [3]에서 설명한 오차를 줄이는 방법을 활용하여 본 논문의 연구에서 표적의 시간지연 추출 정확도를 높이는 처리를 구현했다. 먼저 추출한 표적의 시간지연 값들(T)과 확인 빔의 세 번째 버스트에서 추출된 표적 Hit들의 모호성 있는 표적 거리 값들(Ra3) 및 PRI 값(TPRI)을 이용하여 T의 각 원소들(T(i))에 대해 Tr(i)의 값을 계산한다. 여기서 Tr(i)=mTPRI+2Ra3(idx3)/C, i는 T의 원소에 대한 색인(index, 즉 i는 확인 빔에서 탐지한 표적들의 색인), 그리고 m=floor(T(i)/TPRI)이다. 그리고 floor(a)는 실수 a 값에서 소수점 이하 자리 숫자를 버리고 만든 정수를 나타내며, idx3는 i번째 탐지 표적에 해당하는 세 번째 버스트에서 추출한 표적 Hit의 색인이다(idx3에 대한 자세한 설명은 부록을 참고). 그 다음 (T(i)−Tr(i))의 값에 따라 Tr(i)의 값이 T(i)의 측정오차 값 범위 안에 들어가도록 Tr(i)의 값을 다음 식과 같이 조정한다.
여기서 T(i)의 측정오차 값이 (TPRI/2)의 값보다 작다는 전제 조건을 필히 만족해야 한다. 즉, 식 (1)의 우측 항의 조건을 만족하는 PRI를 운용해야 한다. 본 논문의 연구에서 구현한 확인 빔에서 표적의 시간지연 추출 정확도를 높이는 처리 과정에 대한 자세한 설명은 부록에 기술되어 있다. 이렇게 계산한 Tr로부터 측정오차를 줄인 표적 거리 R=C/2×Tr을 구할 수 있다. 표적의 거리 추출 이후 표적 방향각 및 속도 추출은 탐색 빔에서의 과정과 같은 처리 과정이며, 이렇게 추출한 표적 정보를 이용해서 다음의 추적 빔 또는 확인 빔을 생성하여 운용한다.
그림 4 상단의 추적 빔 운용 아래에 표적 추적 빔에 대한 신호처리 흐름을 표현하였다. 레이다 신호 획득, 플랫폼 속도 보상, 펄스 압축, 그리고 도플러 처리는 탐색 빔에서의 과정과 같은 처리 과정이다. 앞에서 언급하였듯이 추적 빔은 추적하고 있는 표적을 최적으로 탐지할 수 있는 파형을 선정하여 운영한다. 그러므로 추적 빔에서의 PRF가 MPRF의 범위이거나, HPRF의 범위일 수도 있다. 그래서 추적 빔에서의 CFAR 처리는 탐색 및 확인 빔에서의 과정과 같으나, MPRF를 사용하느냐, HPRF를 사용하느냐에 따라 보다 특화된 방법들을 선택하여 사용할 수 있다[4]. Hit 클러스터링 및 표적 방향각 추출은 탐색 빔에서의 과정과 같은 처리 과정이며, 표적 거리/속도 추출은 추적 필터로부터 예측한 표적의 거리/속도 값을 이용하여 모호성을 해결한 거리/속도를 구해내는 과정이다. 추적 빔에서 모호성 해결한 거리/속도 추출은 참고문헌 [2]에서 설명한 방법을 사용하였다. 이렇게 구해진 표적 정보(표적의 방향각, 거리, 속도 정보)가 추적 필터에 전달된다. 그 다음 추적 필터로부터의 정보를 이용하여 다음번 해당 표적에 대한 추적 빔을 방사할 때에 표적의 위치를 예측하고, 예측된 위치의 해당 표적을 최적으로 탐지할 수 있는 추적 빔을 운용한다.
본 논문에서 설계한 방법으로 표적을 탐지/추적하기 위해서는 앞에서 언급하였듯이 탐색과 확인 빔 사이에 빠른 전개가 이루어져야 한다. 즉, 신호처리 시간이 짧아야 한다. 빠른 신호처리 시간을 위해 대용량의 데이터를 처리하는 과정들(플랫폼 속도 보상, Dechirp, 펄스 압축, 도플러 처리, CFAR 처리)에서 다중 코어(core)를 이용한 병렬처리를 하여 처리시간을 줄였다.
Ⅳ. 수송기 탑재 시험 환경과 전방 고속표적 탐지
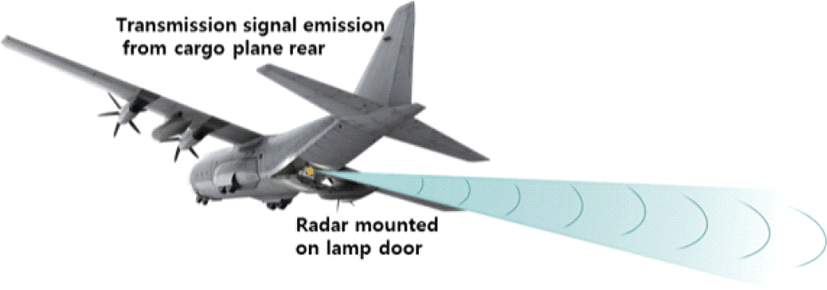
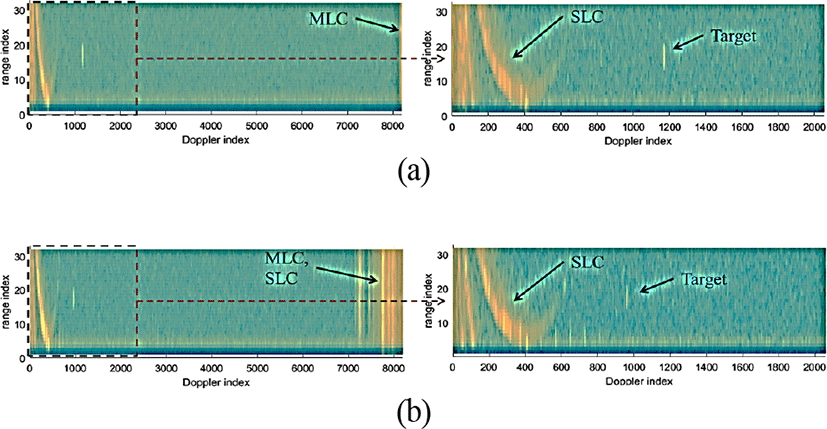
AESA 레이다에 기반한 전방 고속표적 탐지/추적 모드을 위해 본 논문에서 제시한 파형 및 신호처리 알고리즘 설계에 따라 기능을 구현하고, 비행시험을 통해 구현한 기능을 확인하였다. AESA 레이다를 수송기의 램프도어에 설치하고 램프도어 개방 상태에서 후방으로 송신 신호를 방사했다. 그리고 표적기로서 전투기가 사용되었다. 수송기의 특성상 플랫폼의 고도는 대체로 낮았으며, 플랫폼의 기동은 적었다. 그림 5는 본 논문에서의 비행시험 환경을 표현한 그림이다. 일반적으로 항공기 레이다는 항 공기의 앞 쪽에 장착되어 항공기가 이동하는 방향으로 빔을 방사하지만(전방 방사), 본 논문의 비행시험은 수송기의 뒤쪽으로 빔을 방사하면서(후방 방사) 획득하므로 비행기의 이동방향과 빔의 방사방향이 반대가 되는 특수한 상황이 된다. 이런 수송기 탑재 비행시험 환경에서 고려해야할 사항은 항공기 후방으로 빔을 방사하면 항공기 의 앞 쪽으로 빔을 방사할 때와는 반대로 지면 반사 신호의 도플러가 형성된다는 점이다. 영(zero) 도플러 또는 주엽 클러터 중심 도플러를 기준으로 지면 반사 신호의 도플러가 전방 방사 때와는 반대로 형성된다. 그림 3(a)와 그림 3(c)을 본 논문의 수송기 탑재 시험 환경을 기준으로 다시 그리면 그림 6과 같다. 그림 3(a)와 그림 6(a)를 서로 비교해 볼 수 있으며, 주엽클러터(MLC) 및 부엽클러터(SLC)의 위치가 서로 반대임을 볼 수 있다. 그리고 그림 3과 그림 6에서 표적의 절대속도가 같다고 가정했을 때 표적의 도플러 위치가 그려져 있다. 그림 3(c)와 그림 6(b)를 서로 비교해 볼 수 있다. 그림 3과 그림 6의 비교로 알 수 있듯이 안테나 전방에서 접근하는 표적을 탐지할 때, 후방 방사의 경우는 전방 방사보다 클러터 영향 없이 깨끗하게 탐지할 수 있는 영역이 줄어든 것을 볼 수 있다. 수송기 탑재 시험 환경은 안테나 전방에서 접근하는 표적을 클러터 영향 없이 탐지할 수 있는 최저 탐지 속도 면에서 상당히 손해 보는 것을 알 수 있다. 그리고 그림 6(b)에서 보듯이 먼 거리의 표적은 클러터 영역으로 표적이 들어갈 가능성이 커져서 표적 탐지 거리 면에서도 상당히 손해 보는 것을 알 수 있다. 즉, 수송기 탑재 시험 환경인 후방 방사는 일반적인 전방 방사보다 표적의 최저 탐지 속도 및 최대 탐지 거리의 측면에서 성능 저하가 발생함을 예상할 수 있다. 그림 7은 본 논문의 비행시험에서 획득한 레이다 반사 신호로부터 구한 거리/도플러 맵 을 보여준다. 그림 7의 거리/도플러 맵들에서 가로축은 도플러(Doppler) 색인, 세로축은 거리(range) 색인을 나타낸다. 그림 7(a)는 그림 6(a)와 같은 파형의 버스트를 운영하여 획득한 거리/도플러 맵의 예로, 그림 4의 탐색 빔 운용 아래에 있는 신호처리 과정 들인 플랫폼 속도보상, 펄스 압축, 도플러 처리를 거친 후의 거리/도플러 맵이다. 그림 7(a)의 좌측 거리/도플러 맵에서 점선 사각 영역을 확대하여 표현한 것이 그림 7(a)의 우측 그림이다. 그림 7(a)에서 주엽클러터, 부엽클러터, 표적 위치를 그림 6(a)와 비교하여 확인해 볼 수 있다. 주엽클러터의 중심은 플랫폼 속도 보상 처리 때문에 영 도플러에 위치해 있다. 표적은 안테나 전방에서 빠른 속도로 접근하는 표적이다. 그림 7(b)는 그림 6(b)와 같은 파형의 버스트를 운영하여 획득한 거리/도플러 맵의 예로, 그림 4의 확인 빔 운용 아래에 있는 신호처리 과정 들인 플랫폼 속도보상, Dechirp, 펄스 압축, 도플러 처리를 거친 후의 거리/도플러 맵이다. 그림 7(b)에서 표적 위치는 표적의 거리에 의해 그림 7(a)의 표적 위치보다 더 낮은 도플러 주파수 위치에 있다. 그림 7(b)의 주엽 및 부엽클러터도 지면 반사 지점들의 거리에 의해 클러터들이 낮은 도플러 위치로 퍼져 이동한 것이 폴딩되어(folded), 높은 도플러 색인 위치(색인 7200에서 8192까지의 영역)로 나타난 것을 볼 수 있다.
Ⅴ. 전방 고속표적 탐지/추적 시험 결과
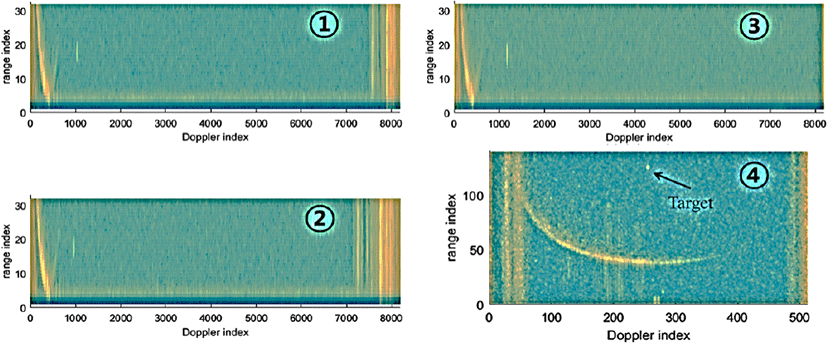
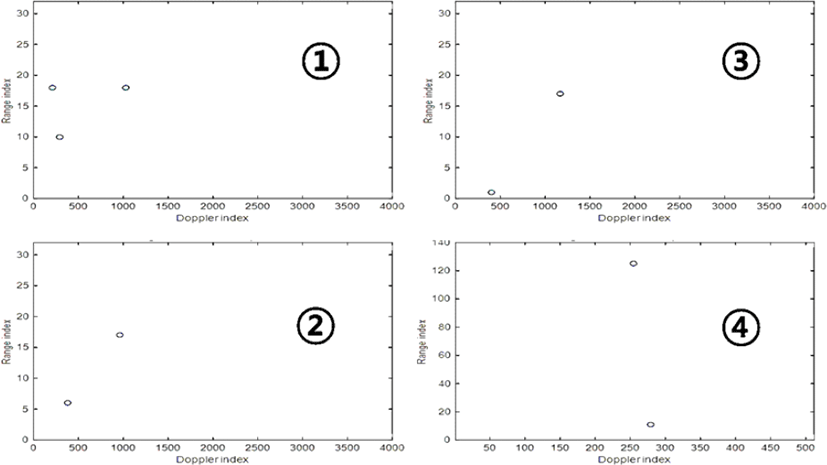
이 절에서는 제시한 방법으로 AESA 레이다의 수송기 탑재 비행 시험을 통해 획득한 결과를 제시한다. 그림 8은 전방 고속표적 탐지/추적을 위한 빔을 운용하여 획득한 거리/도플러 맵 데이터이다. 그림 8의 ①번 거리/도플러 맵은 본 논문에서 사용한 확인 빔의 파형에서 첫 번째 버스트로부터 획득한 것이다. 그림 8의 ②번과 ③번의 거리/도플러 맵은 본 논문에서 사용한 확인 빔의 파형에서 각각 두 번째와 세 번째 버스트로부터 획득한 것이다. 확인 빔을 구성하는 그림 8의 ①, ②, ③번 거리/도플러 맵 데이터로부터 추출한 정보로 표적의 거리 및 도플러, 방향각을 추출한다. 그림 8의 ④번 거리/도플러 맵 데이터는 그림 8의 ①, ②, ③번으로 구성되는 확인 빔에서 추출된 한 표적을 추적하는 추적 빔 버스트로부터 회득한 것이다(참고로 추적 빔은 단일 버스트로 구성된다). 그림 8의 ④번 거리/도플러 맵에서 추적하고 있는 표적의 거리/도플러 셀 위치를 잘 확인할 수 있다. 즉 추적하고 있는 표적을 클러터 영향 없이 최적으로 탐지할 수 있는 파형이 운영된 것을 확인할 수 있다(주엽과 부엽클러터 없는 깨끗한 영역에 표적이 위치하고 있다). 그림 9는 그림 8의 거리/도플러 맵 데이터들에서 CFAR와 Hit 클러스터링 과정을 거친 후의 결과인 표적 Hit 들의 거리 및 도플러 셀 위치를 표현한 것이다. 그림 9의 ①, ②, ③, ④ 그림들은 차례로 그림 8의 거리/도플러 맵 데이터 ①, ②, ③, ④로 부터 나온 결과들이다. 그림 9의 ①, ②, ③의 표적 Hit들의 결과에서 표적의 모호성 없는 거리/도플러의 값을 본 논문에서 제시한 방법으로 추출하게 된다. 이렇게 탐지한 표적을 추적하는 파형을 운영하여 획득한 것이 표적 Hit들의 결과가 그림 9의 ④번 그림이다. 그림 8의 ④번과 그림 9 ④번을 비교해 보면 알 수 있듯이 그림 9의 ④번 그림에서 상단 위치에 추적하고 있는 표적의 Hit가 잘 나타남을 확인할 수 있다. 그림 10은 본 논문에서 설명한 비행시험을 통해 표적 탐색 빔, 확인 빔 및 추적 빔을 운영하여 획득한 데이터들을 신호처리 하여 최종적으로 획득한 탐지된 표적의 정보들을 예로서 나타낸 것이다. 그림 10(a)는 탐색 빔을 운영하여 탐지된 표적의 추출된 정보의 예이다. 그림 10(a)의 첫 행은 빔 조향각 및 탐지된 표적의 모노펄스 각도 값(빔 조향각 중심 대비 표적 위치의 고각 및 방위각 차이)을 나타낸다. 두 개의 표적이 탐지되었으며, 그 중에 하나의 표적에 대한 값을 표시하고 있다. 그림 10(a)의 둘째 행은 탐지된 표적의 상대속도 및 거리를 나타낸다. 두 개의 탐지된 표적 중에서 하나의 표적에 대한 값을 표시하였으며, 그 값은 179.3 m/s 및 0.89 km이다. 탐색 빔에서 추출된 상대속도는 모호성이 없는 실제 값이며, 거리는 모호성이 있는 실제 표적의 거리 값이 아니다. 그림 10(b)는 그림 10(a)에서 탐지된 하나의 표적(그림 10(a)에서 거리 및 속도를 표시했던 표적)에 대해 확인 빔을 운영하여 탐지된 표적의 추출된 정보의 예이다. 추출된 모노펄스 값 및 상대속도, 거리 값 등을 그림 10(a)와 같은 방식으로 나타내고 있다. 하나의 표적만 거리모호성이 해결되어 추출되었고 그 추출된 표적 정보를 표시했으며, 상대속도는 179.1 m/s로 거리는 79.86 km로 추출되었다. 동일 표적에 대해 추출된 정보이므로 확인 빔과 탐색 빔의 상대속도가 비슷하게 추출되었으며, 거리는 확인 빔에서 모호성이 해결되어 추출되었다. 확인 빔 등에서 추출된 표적의 방향각 (조향각과 모노펄스 각도) 및 상대속도, 거리 값을 바탕으로 파형을 결정[2]하여 운영한 추적 빔에서 탐지된 표적의 추출된 정보의 예가 그림 10(c)이다. 추출된 모노펄스 값 및 상대속도, 거리 값 등을 그림 10(b)와 같은 방식으로 나타내고 있다. 그림 10(b)에서 상대속도와 거리가 179.1 m/s와 79.86 m인 표적을 추적하려고 운영한 추적 빔에서 탐지된 표적들을 표시한 것이 그림 10(c)이다. 그림 10(c)에서 탐지된 표적 2개 중에서 그림 10(b)의 속도와 거리가 179.1 m/s와 79.86 km인 표 적과 연관성이 높은 표적에 대해 그 추출된 표적 정보를 표시하였다. 그 상대속도와 거리는 178.5 m/s와 79.66 km로 추출되었다. 즉 목적한 표적을 추적 빔이 잘 탐지한 것을 확인할 수 있다. 본 논문에서 그림 10(c)의 탐지된 표적 정보는 추적 필터로 전달되며, 추적 필터에서는 그림 10(c)에서 탐지된 2개의 표적 중(또는 다수의 표적 중)에서 추적하고 있던 표적의 이전 표적 정보와의 연관성을 조사하여 하나 만을 목적한 실제 표적으로 선택하고, 나머지 표적들은 버린다(만약 탐지된 표적들 모두가 추적 중인 표적과 연관성이 없다면 모두 버린다).
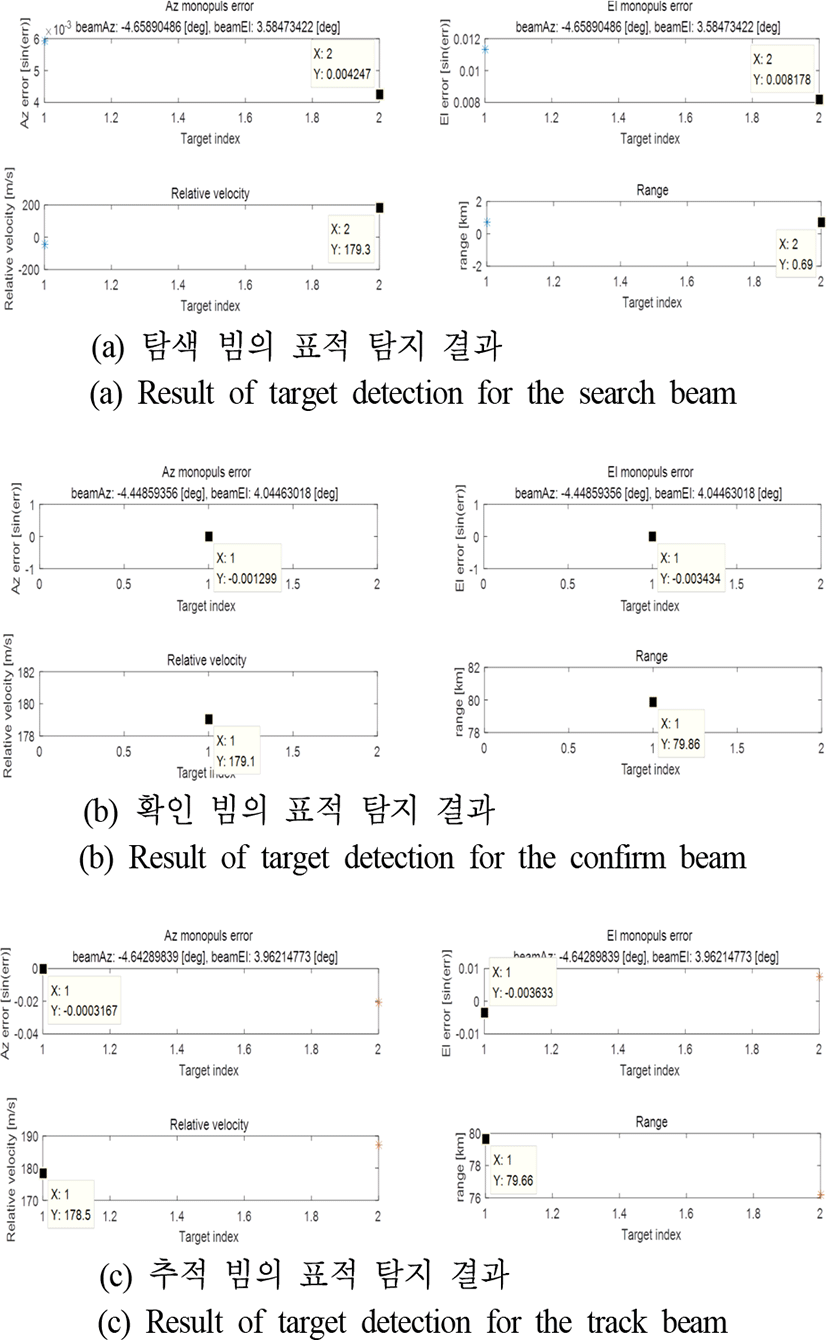
이 절에서 보여준 비행시험 결과들로부터 본 논문에서 제시한 HPRF 파형을 기반으로 하는 전방 고속표적 탐지/추적 방법이 잘 동작함을 확인할 수 있다. 수송기 탑재 비행시험에서, 실제로 탐색 빔에서 상대속도 약 179 m/s인 표적을 탐지하고, 해당 표적을 약 80 km부터 시작하여 근거리까지 추적을 유지하며 표적을 탐지/추적하였다.
Ⅵ. 결 론
AESA 레이다를 이용한 전방 고속표적 탐지모드를 위하여 HPRF 파형의 설계 방법 및 표적 탐지/추적을 위한 파형 운용 방법과 신호처리 알고리즘 설계를 제시하였다. 본 논문에서 제시한 방법으로 전방 고속표적 탐지 기능을 AESA 레이다를 수송기에 탑재한 특수한 시험환경에서 비행시험을 통해 확인하였다. 본 논문의 시험환경의 특수성을 설명하였으며, 비행시험 결과로부터 고속으로 접근하는 전투기 표적을 효과적으로 탐지/추적함을 확인하였다. 즉, 제시한 방법에 의한 전방 고속표적 탐지 기능이 동작함을 확인하였다. 플랫폼의 롤(roll) 기동 등이 심한 상태에서도 제시한 방법이 잘 동작하는지 확인을 위해 추가적인 비행시험이 필요하다.
부 록
이 부록에서는 본 논문의 연구에서 구현한 확인 빔에서 FM ranging 기법에 기반한 표적의 시간지연(표적 거리)을 추출하는 처리 및 이 값의 정확도를 높이는 처리 과정에 대해 자세한 기술한다. 그림 11은 식 (3)을 이용하여 표적 거리를 추출하는 처리 과정을 설명한 것이다. 그림 11에서 보듯이 확인 빔을 이루는 3개의 버스트에서의 표적 Hit정보들이 버스트 순서로 입력되면 해당 버스트에 따른 처리를 한다. 그림 11의 중간 빈 공간 부분(※ 표시 부분)에 각 처리 과정에서 사용되는 상수 및 변수, 함수에 대한 설명을 첨가하였다. 먼저 첫 번째 버스트에 대한 ①번 과정은 첫 번째 버스트에서 획득한 표적 Hit들의 비트 주파수를 관련 배열 변수 F1에 저장하는 과정이다. Nhit1은 첫 번째 버스트에서 획득한 표적 Hit들의 개수이다. ②번 과정은 두 번째 버스트에서 획득한 표적 Hit들의 비트 주파수를 관련 배열 변수 F2에 저장하고(Nhit2은 두 번째 버스트에서 획득한 표적 Hit들의 개수이다), ③번 과정은 식 (3)의 좌측 변에 있는 식에 기반하여 첫 번째와 두 번째 버스트들의 표적 Hit들을 모든 경우의 방법으로 서로 짝지어 식 (3)의 좌측 변에 있는 식에 해당하는 값을 구해 행렬 변수 D에 저장한 것이다. 여기서 n은 (n+1)/n=kFM2/kFM1을 만족한다. ④번 과정은 세 번째 버스트에서 획득한 표적 Hit들의 비트 주파수를 관련 배열 변수 F3에 저장하는 과정이다. Nhit3은 세 번째 버스트에서 획득한 표적 Hit들의 개수이다. ⑤번 과정은 D에 저장된 개별 원소와 F3에 저장된 개별 원소를 모든 경우의 방법으로 서로 짝지어 D의 원소에서 F3의 원소를 뺀 값을 배열 변수 S에 저장하는 과정이다. 배열 변수 S의 원소는 식 (3)의 관계식을 만족하는 각 버스트의 표적 Hit를 하나씩 가지는 트리오(trio)들을 찾기 위해서 ((n+1) fb1−n fb2−fd)의 값을 저장하고 있는 것이다. S에서 ((n+1) fb1−n fb2−fd)≺Cws 의 조건을 만족하는 이런 트리오들을 찾는다면, 이런 트리오들은 오표적 및 고스트 표적이 아닌 실제 표적이 형성한 트리오가 된다. 즉, 오표적 및 고스트 표적을 배제한 실제 표적의 모호성 없는 거리를 추출할 수 있을 것이다. ⑥번 과정은 앞에서 설명한 트리오들을 빠르게 찾기 위해 S의 원소들을 오름차순 정렬하여 배열 변수 P에 저장하고 그 정렬된 S 원소들의 색인 순서를 배열 변수 I 에 저장하는 과정이다. 참고로 배열 S의 한 원소가 3개 버스트의 어떤 표적 Hit들의 조합으로 이루어졌는지를 찾고 싶으면 식 (5)를 이용하면 된다.
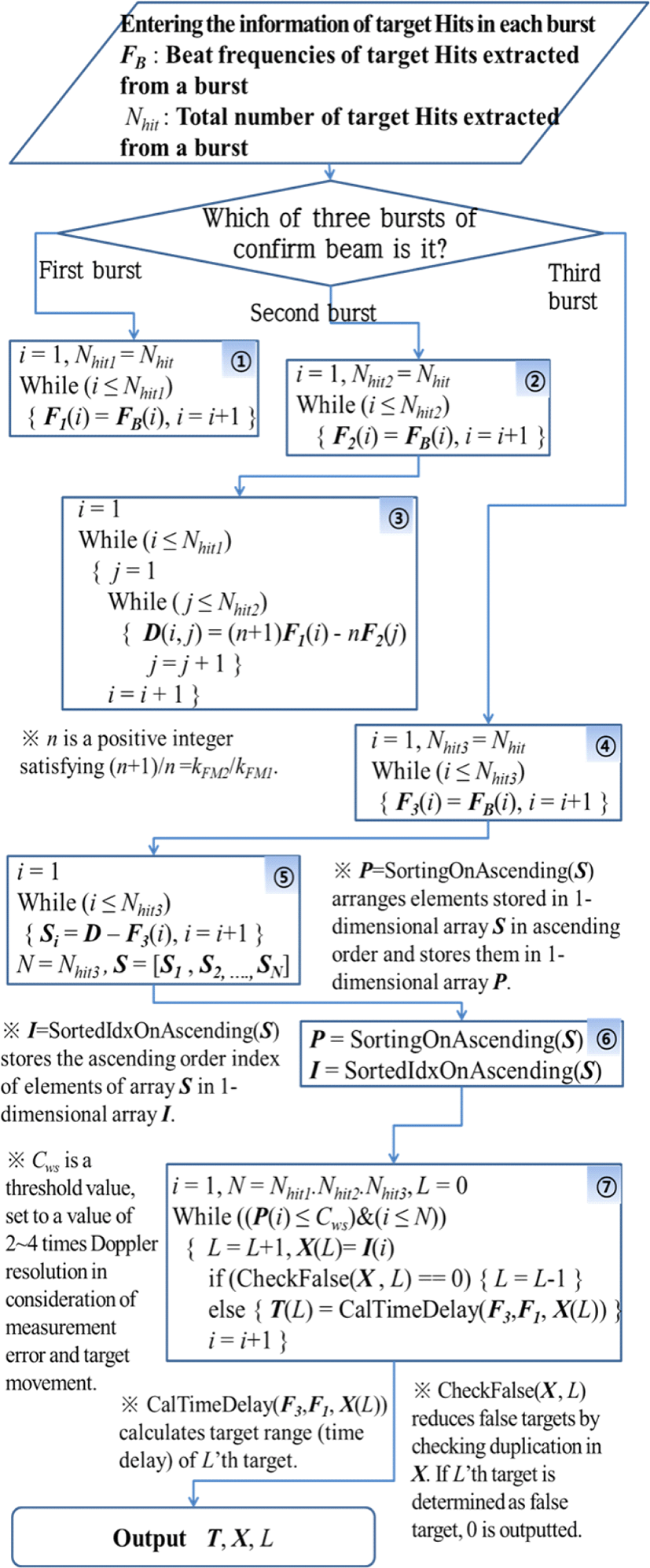
식 (5)에서 Hitidx1, Hitidx2, 그리고 Hitidx3은 각각 차례로 첫 번째, 두 번째, 그리고 세 번째 버스트에서 표적 Hit에 대한 색인이다. 그리고 sidx는 S의 원소들의 색인, floor(a)는 실수 a 값에서 소수점 이하 자리 숫자를 버리고 만든 정수, 그리고 mod(a,b)는 a−b(floor(a/b)) 값을 나타낸다. tempidx=mod((sidx−1)/(Nhit1Nhit2))+1 이다. ⑦번 과정은 표적의 거리를 나타내는 표적에 대한 송신과 수신 사이의 시간지연을 찾는 과정이다. P의 원소에서 ((n+1) fb1−n fb2−fd)≺Cws 조건을 만족하는 원소를 찾고, 그 원소와 같은 색인 위치의 I 의 원소 값으로 이미 추출한 표적에 대한 트리오에 속한 버스트 별 표적 Hit들이 존재하는지를 검사하여 오표적 및 고스트 표적 인지 점검(CheckFlase())한 후 실제 표적만 시간지연 값을 계산(CalTimeDelay())하여 배열 변수 T에 저장한다. 그림 12는 그림 11에서 추출한 트리오가 오표적 및 고스트 표적 인지 점검하는 CheckFalse()에 대한 기능과 추출한 트리오로부터 표적의 시간지연을 계산하는 CalTimeDelay()에 대한 기능을 설명한 처리과정을 나태난 그림이다. 그림 12에서 표적의 시간지연은 식 tr=(fd−fb1)/kFM1을 이용하여 계산하고 있다.

참고문헌 [3]의 측정 오차를 줄이는 방법을 활용하여 본 논문에서 구현한 표적의 시간지연 추출 정확도를 높이는 과정은 그림 13에 제시되어 있다. 먼저 그림 11의 과정에서 추출한 표적의 시간지연 값들(T)과 세 번째 버스트에서 추출된 표적 Hit들의 모호성 있는 표적 거리 값들(Ra3) 및 PRI 값(TPRI) 등을 입력받고, Tr(i)=floor(T(i)/ TPRI)×TPRI+2/C×Ra3 (idx3)을 계산한다. 여기서 i는 T의 원소에 대한 색인이며 idx3는 식 (5)의 Hitidx3와 같은 의미의 값을 가진다. 그 다음 (T(i)−Tr (i))의 값 조건에 따라 Tr(i)의 값이 T(i)의 측정오차 값 범위 안에 들어가도록 Tr(i)의 값을 조정한다. 그림 13의 과정으로 계산한 출력 Tr로부터 측정오차를 줄인 표적 거리 R=C/2×Tr을 구할 수 있다.







