PN 유도 기반 능동 RF 탐색기 조우 시나리오에서 반복형 능동 유인체 대응에 따른 공중 플랫폼 생존성 분석

Ⅰ. 서 론

공중 플랫폼에 접근하는 RF 탐색기로부터 플랫폼의 생존성을 확보하는 것은 매우 중요하다. RF 탐색기로부터 플랫폼을 보호하기 위한 하나의 방법으로 전자방해책(Electronic Counter Measure: ECM)이 사용되어 왔다. ECM 기법 중 하나인 반복형 능동 유인체(active decoy)는 플랫폼으로부터 사출되어 RF 탐색기에서 수신된 신호를 증폭하여 재방사하는 물체로 RF 탐색기에 재밍 공격을 가하여 적 레이다를 기만하며 저렴한 비용과 높은 효율성으로 각광받아왔다^[1]. 유인체의 운용에 따른 RF 탐색기에 대한 기만 효과를 분석하기 위해서는 현실성을 반영한 여러 조우 시나리오에서 해석이 가능한 M&S(Modeling & Simulation) 접근법이 필요하다. 이를 위해 플랫폼의 편파에 따른 2D RCS(Radar Cross Section), 플랫폼 운동에 따른 유인체 정확한 궤적 및 자세각, 탐색기 및 유인체의 편파, 방사 패턴, 안테나 이득 등의 RF 제원(spec), 탐색기의 레이다 신호처리 모듈 모사 등과 같은 고려사항이 요구되며, 이는 최종 시뮬레이션 결과에 큰 영향을 미친다. 최근 위 기술한 사항들을 고려하여 유인체의 성능을 분석하기 위한 이론적인 M&S 접근법이 제안되었다^[2],^[3]. 그러나 이는 플랫폼에 접근하는 RF 탐색기가 아닌 지상 추적 레이다에 대한 유인체의 성능 분석으로 국한된다.

본 논문에서는 RF 탐색기에 대한 유인체의 기만 효과 및 플랫폼 생존성 분석을 다룬다. RF 탐색기의 운동으로는 간편한 하드웨어 구현(hardware implementation)으로 많은 RF 탐색기에 보편적으로 사용되는 비례항법(Propotional Navigation: PN) 유도 법칙을 고려한다. Ⅱ절에서 제안하는 M&S 접근법 및 모델링 방법을 기술하며 Ⅲ 절에서는 RF 탐색기 모델링 방법에 대해 기술한다. Ⅳ절에서는 여러 조우시나리오에서 RF 탐색기에 대한 플랫폼의 생존 영역을 도출하며 이에 대한 분석을 제시한다.

Ⅱ. M & S 접근법

그림 1은 조우 시나리오에서 M&S 접근법에 대한 요약을 나타낸다. RF 탐색기는 안테나 빔을 플랫폼의 위치로 조향하고 플랫폼의 예상요격지점으로 발사되며 플랫폼은 유인체를 사출하고 기동을 수행한다. 플랫폼의 기동은 유인체의 공력과 모멘트에 영향을 주기 때문에 유인체의 운동에 영향을 미친다. 따라서 정확한 유인체의 궤적 해석을 위해, 전산유체역학(Computational Fluid Dynamics: CFD) 해석을 통해 유인체의 간섭유동장 데이터베이스를 구축하고, 이를 기반으로 6 자유도(Degree of Freedom: DOF) 방정식의 해를 구해야 한다^[4]. RF 탐색기는 매 펄스 반복 시간(Pulse Repetition Time: PRT)마다 chirp 신호를 송/수신한 후 레이다 신호 처리를 통해 표적(플랫폼 혹은 유인체) 위치를 추정하며, 유도 법칙에 따라 추정된 표적 위치로 유도된다. 이 때, 두 물체로부터 수신되는 신호를 계산하기 위해서는 플랫폼의 편파에 따른 2D 모노스태틱 레이다 시그니처 데이터베이스가 필요하며 유인체의 RF 제원을 고려하여야 한다. 매 PRT 동안 두 물체의 움직임은 무시할 수 있으며, 탐색기의 안테나 주엽(main lobe)은 공중에 위치한 두 물체를 향하며 지상 표면에 의한 반사에 의해 부엽(side lobe)에 수신되는 신호의 크기는 매우 작기 때문에 무시 가능하다. 따라서 두 물체로부터 반사되어 탐색기에서 수신되는 시간 영역(time-domain) 전력은 자유 공간(free space) Friis 전송 방정식^[5]을 통해 계산이 가능하다. 위에 기술한 플랫폼 기동에 따른 유인체의 운동 해석 방법과 시간 영역 전력 계산을 위한 방법은 참고문헌 [2]에 자세히 기술되어 있으며, 본 논문에서는 이와 동일한 모델링을 고려한다. RF 탐색기의 레이다 신호 처리 및 유도에 대한 모델링은 다음 절에 자세히 기술한다.

그림 1. | Fig. 1. M&S 접근법 요약 | Summary of M&S approach.

Download Original Figure

Ⅲ. 능동 RF 탐색기 모델링

RF 탐색기에서 송신되는 chirp 신호는 다음과 같다.

여기서 w는 캐리어 각주파수(angular frequency)이고, μ는 chirp rate [Hz/sec]이며 rect(·)는 사각 윈도우(rectangular window)를 나타낸다. 유인체로부터 수신되는 재밍 전력을 J, 플랫폼으로부터 반사되는 전력을 S라 할 때, n번째 PRT에 수신 chirp 신호는 다음과 같다.

여기서 ARF_p와 ARF_d는 플랫폼과 유인체에 대한 탐색기 안테나의 배열계수(array factor)를 나타낸다. 또한 R_p와 R_d는 각각 탐색기로부터 플랫폼과 유인체까지의 거리를 나타내며 c는 빛의 속도를 나타낸다. S⁽ⁿ⁾과 J⁽ⁿ⁾은 Friis 전송 방정식을 기반으로 계산이 가능하며 자세한 절차는 참고문헌 [2]에 기술되어 있다. 안테나 배열계수 ARF는 탐색기 안테나의 지역좌표계(local coordinates)에 정의되며 안테나 요소들의 가중치(weight)에 의해 합(sum) 패턴 Σ과 차(difference) 패턴 Δ_el, Δ_az로 계산할 수 있다^[6]. 여기서 Δ_el과 Δ_az는 각각 고각 및 방위각 방향으로의 차 패턴을 나타낸다. 합 패턴 및 차 패턴을 고려하여 기저대역(baseband)에서 샘플링된 신호 $s^{\Sigma }\left[k\right],s_{el}^{\Delta }\left[k\right],s_{az}^{\Delta }\left[k\right]$를 계산할 수 있다. 이들은 펄스압축(pulse compression)^[7] 후 $s_c^{\Sigma }\left[k\right],s_c^{{\Delta }_{el}}\left[k\right],s_c^{{\Delta }_{as}}\left[k\right]$로 계산되며, 합 패턴 신호 s^Σ[k]를 thresholding 처리하여 표적 거리 $\tilde{R}$를 추정한다. 추정된 표적 거리의 range bin k_max에서 모노펄스 비율은 다음과 같다^[6].

본 논문에서는 크기 비교 모노펄스(amplitude-comparison monopulse) 시스템을 고려한다^[6]. 식 (3)으로부터 탐색기의 안테나 빔 조향각도 ${\theta }_0^{\left(n\right)},{\varphi }_0^{\left(n\right)}$으로부터 벗어난 표적의 각도 정보를 다음과 같이 추정할 수 있다.

탐색기의 지역좌표계 ${\widehat{x}}_m,{\widehat{y}}_m,{\widehat{z}}_m$에서 추정된 표적 정보는 전역좌표계로 변환되며, 이는 다음과 같다.

위 n번째 PRT에서 관측된(observed) 표적 3D 위치 정보는 예측(prediction)과 스무딩(smoothing)을 위해 추적필터(tracking filter)를 거치며, 본 논문에서는 αβγ필터를 고려한다. n번째 관측 후 스무딩된 표적의 위치 ${\overrightarrow{r}}_s$, 속도 ${\overrightarrow{v}}_s$, 가속도 ${\overrightarrow{a}}_s$는 αβγ 필터를 통해 다음과 같이 계산된다^[8].

여기서 ${\overrightarrow{r}}_p$는 예측된 3D 표적 위치를 나타내며, T는 PRT를 나타낸다. 또한 식 (5)의 초기조건은 다음과 같다. ${\overrightarrow{r}}_s^{\left(1\right)}={\overrightarrow{r}}_p^{\left(2\right)}={\overrightarrow{r}}_0^{\left(0\right)},{\overrightarrow{v}}_s^{\left(1\right)}={\overrightarrow{a}}_p^{\left(2\right)}=0$. α, β, γ는 스무딩 계수(smoothing coefficient) η에 의해 다음과 같이 계산된다.: α=1-η³, β=1.5(1-η)² (1+η), γ=(1-η)³, 0≤η≤1. 본 논문에서는 잡음에 의한 추정 오차를 최소화하기 위한 레이다 모델을 고려하여^[8] 높은 스무딩 계수인 η=0.99를 가정한다. 식 (5)로부터 계산된 스무딩 표적의 위치와 속도를 기반으로 탐색기의 자세를 표적 방향으로 유도한다. PN 유도 법칙^[9]은 탐색기의 속도 벡터를 LOS(Line-Of-Sight)의 회전율(rotation rate)에 비례하여 회전한다(그림 2 참조). 표적의 위치, 속도를 ${\overrightarrow{R}}_t\left(={\overrightarrow{r}}_s\right),{\overrightarrow{V}}_t\left(={\overrightarrow{v}}_s\right)$, 탐색기의 위치 속도를 ${\overrightarrow{R}}_m,{\overrightarrow{V}}_m$로 표기할 때, PN 유도 법칙을 기반으로 탐색기의 가속 명령 벡터(acceleration command vector)는 다음과 같다.

그림 2. | Fig. 2. RF 탐색기 및 표적 전개 기하학 | RF seeker-target engagement geometry.

Download Original Figure

여기서 ${\overrightarrow{R}}_{mt}={\overrightarrow{R}}_t-{\overrightarrow{R}}_m,{\overrightarrow{V}}_{mt}={\overrightarrow{V}}_t-{\overrightarrow{V}}_m$이다. N_p는 비례 상수이며, 일반적으로 3과 5사이의 양의 실수 값으로 설계되며^[9], 본 논문에서는 평균값인 N_p=4를 가정한다. 또한 $\overrightarrow{\Omega }=\left({\overrightarrow{R}}_{mt}\times {\overrightarrow{V}}_{mt}\right)/\left({\overrightarrow{R}}_{mt}·{\overrightarrow{R}}_{mt}\right)$는 회전 벡터를 나타낸다. 식 (6)에서 계산된 가속 명령 벡터는 매 PRT마다 반복적으로 표적 방향으로 유도(guide)되며, 반복절차는 다음과 같다.

식 (6)의 가속 명령 벡터의 크기(부하율: load factor)는 일반적으로 제한되며 본 논문에서는 $\max \left(\left|{\overrightarrow{n}}_c\right|\right)=12g\left(g=9.18m/s^2\right)$로 고려한다^[9].

Ⅳ. 시뮬레이션 결과 및 분석

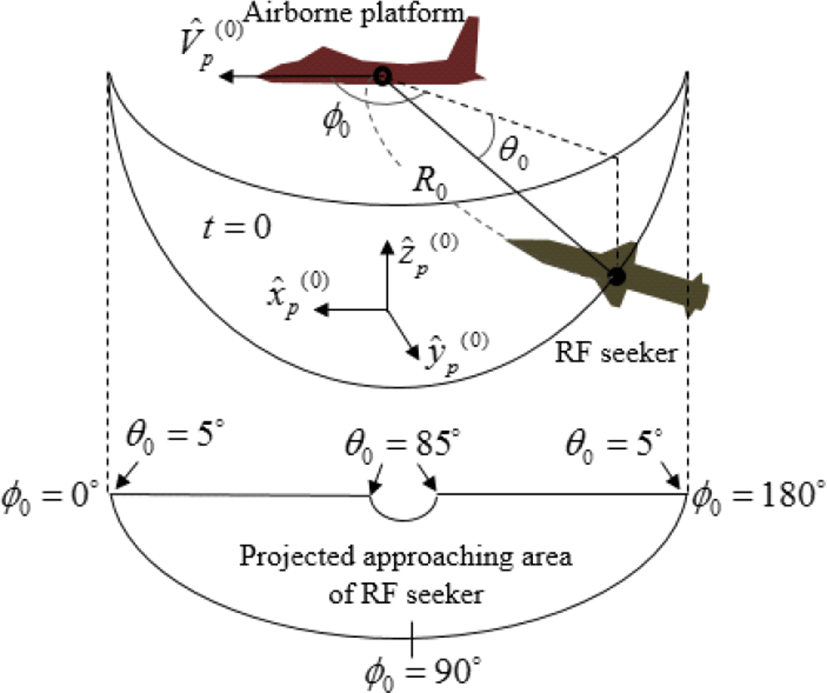
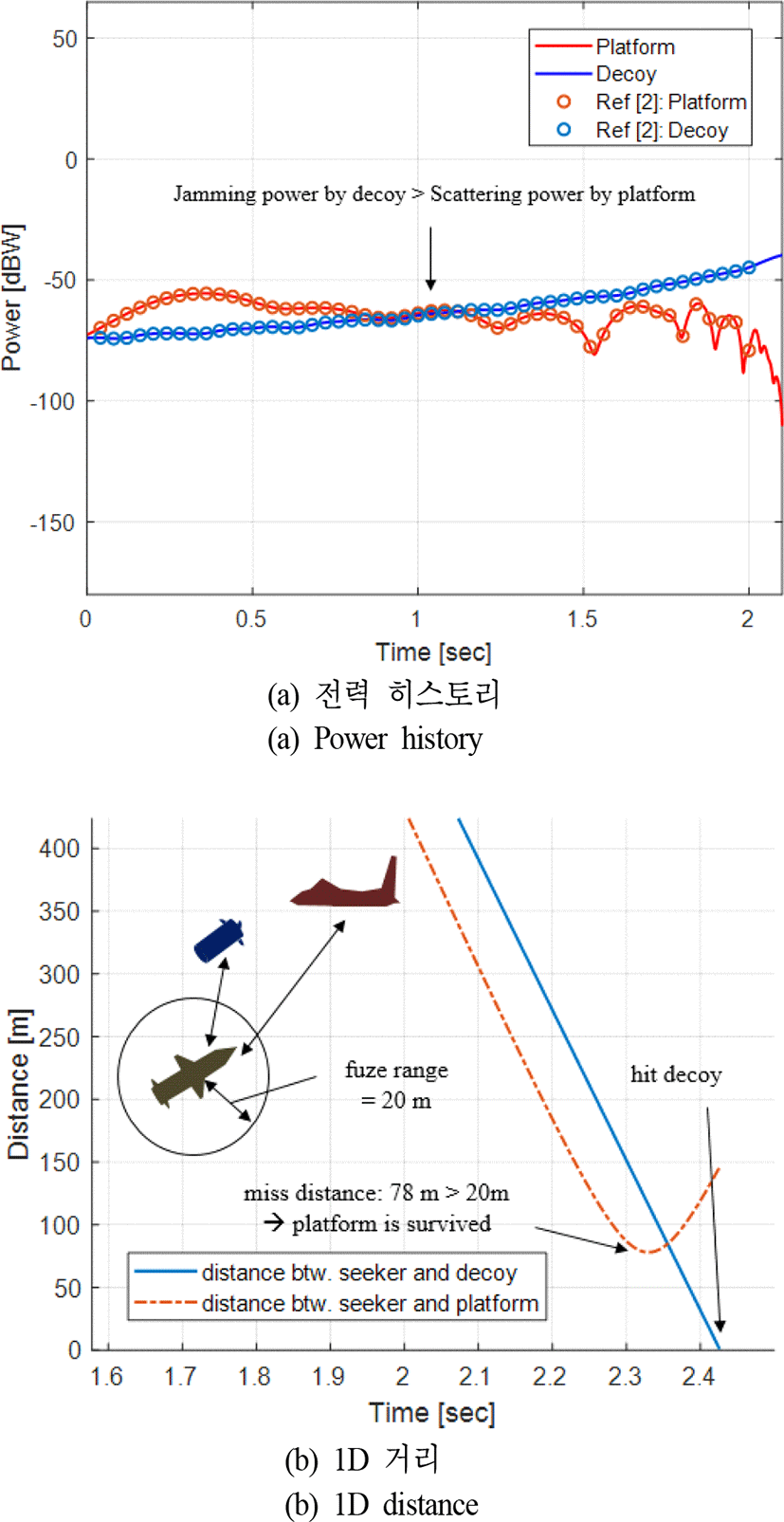
그림 3은 동적 시뮬레이션 순서도를 나타낸다. 플랫폼, 유인체, 탐색기의 초기조건을 설정한 후 탐색기의 PRT마다 각 물체들은 위치를 갱신한다. 추정된 표적 정보(위치 및 속도)를 기반으로 탐색기는 속도벡터를 갱신하며 표적의 요격 혹은 누락(missing) 시 시뮬레이션은 종료되며 플랫폼에 대한 탐색기의 miss distance를 계산한다. 표적(플랫폼 혹은 유인체)가 탐색기의 근접신관거리(proximity fuze range)^[10] 내에 위치할 경우 요격되었다고 판별한다. 플랫폼의 기동 및 속도는 플랫폼의 생존성에 영향을 미치는 중요한 요소이다^[9]. 따라서 본 논문에서는 이에 대한 효과를 분석하기 위해 고려하는 플랫폼 및 유인체의 동적 시나리오는 표 1과 같다^[2]. 유인체의 사출 위치와 각도는 플랫폼의 지역좌표계에서 정의된다(참고문헌 [2] 참고). 플랫폼의 기동(선회비행 혹은 직선비행) 및 플랫폼의 기동 속도(0.4 Mach 혹은 0.8 Mach)의 조건 변화에 따라 유인체를 운용하는 시나리오에서 플랫폼의 생존성을 확인한다. RF 탐색기의 여러 접근 거리 및 방향에 대해 유인체의 재밍에 따른 플랫폼 생존성을 분석하기 위해 미사일의 초기 접근 위치를 플랫폼의 초기 지역좌표계 ${\widehat{x}}_p,{\widehat{y}}_p,{\widehat{z}}_p$에서 그림 4와 같이 정의한다. 시뮬레이션 파라미터 및 초기 조건은 표 2에 요약되어 있다^[11]. RF 탐색기의 성능 검증을 위해 먼저 단일 고정 위치(R₀=3 km, θ₀=15°, ϕ₀=0°)에서 발사된 초기조건 하에 시나리오 1에서 플랫폼과 유인체로부터 수신된 전력 히스토리 및 궤적을 분석하면 그림 5와 같다. 그림 5에서 볼 수 있듯이 플랫폼과 유인체로부터 반사되어 RF 탐색기의 수신되는 전력은 참고문헌 [2]에 제안된 방법의 결과와 동일함을 확인할 수 있고, 탐색기는 이 전력을 기반으로 표적을 지속적으로 추적한다. 이 시나리오에서 유인체는 탐색기의 근접신관거리 내에 들어와 소실되며 플랫폼은 2.33초에 RF 탐색기와 플랫폼의 최소거리, 즉 miss distance가 78 m가 되며, 근접신관거리 반경 밖에 놓여 생존성이 보장된다(그림 5(b)). 이는 대략 1.1초 이후부터 유인체로부터 탐색기에 전달되는 재밍 전력이 플랫폼의 산란 전력보다 커지기 시작하여 RF 탐색기가 최대 전력이 수신되는 유인체 방향으로 유도되기 때문이다(그림 5(a)의 수신 전력 히스토리 참조).

그림 3. | Fig. 3. 동적 시뮬레이션 순서도 | Flow chart of dynamic simulation.

Download Original Figure

그림 4. | Fig. 4. 플랫폼 지역좌표계에서 능동 RF 탐색기의 초기 접근 위치 | Initial approaching location of active RF seeker in local coordinates of platform.

Download Original Figure

그림 5. | Fig. 5. RF 탐색기 수신 전력 히스토리, 3D 궤적 및 탐색기와 플랫폼, 유인체 사이의 거리 (시나리오 1) | Power history received by RF seeker, 3D trajectory, and distance between seeker-platform and seeker-decoy (scenario 1).

Download Original Figure

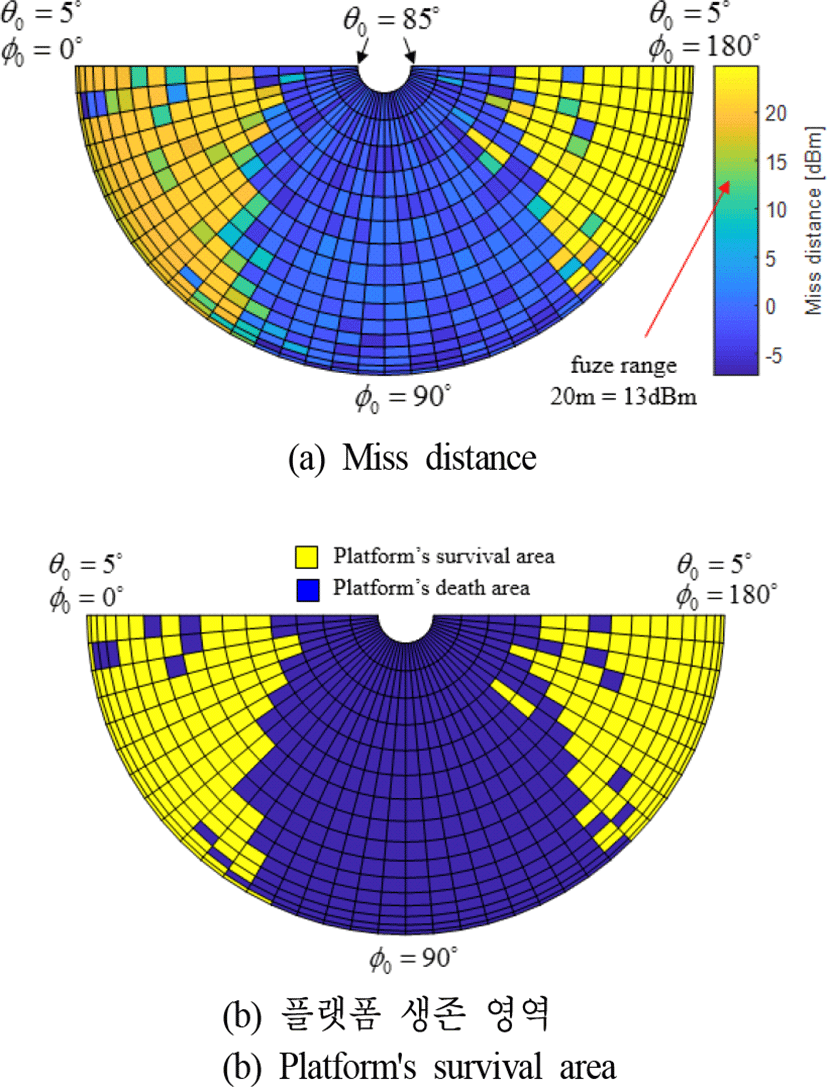
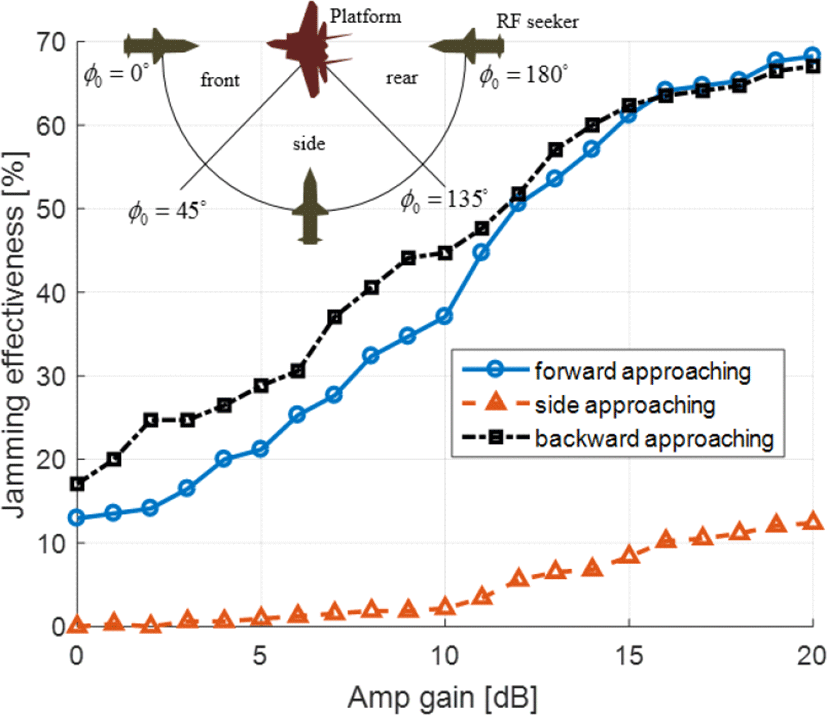
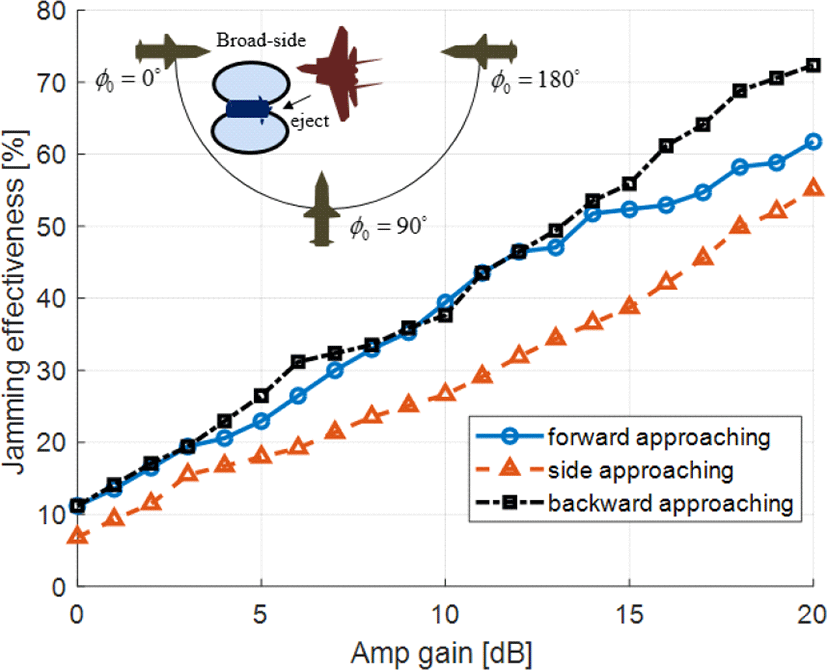
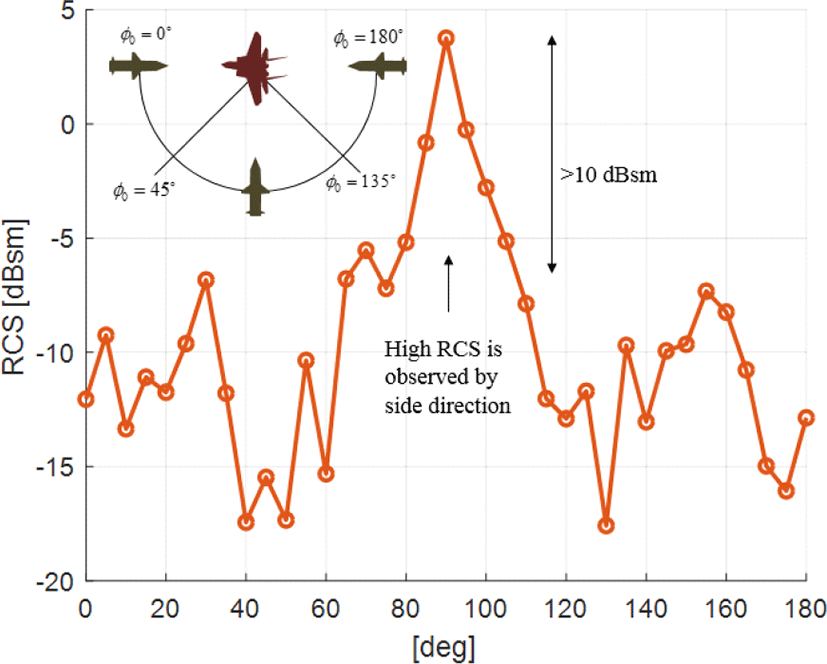
플랫폼의 생존성을 확보하기 위해 유인체의 효율적인 재밍 영역을 찾는 것은 중요하다^[3]. 따라서 본 논문에서는 그림 4에 나타난 RF 탐색기의 여러 접근 시나리오에서 유인체의 재밍이 존재할 경우 플랫폼에 대한 탐색기의 miss distance를 계산하여 플랫폼 생존 영역을 계산하며 이는 그림 6(a)와 같다. RF 탐색기의 접근 거리는 R₀=3 km이며 접근 각도 ϕ₀과 θ₀은 모두 5° 간격으로 샘플링 되었으며, 샘플링 범위는 각각 ϕ₀=0～180°와 θ₀= 5～85°이다. Miss distance가 근접신관거리 20 m(=13 dBm) 내/외에 위치한 경우 플랫폼은 소실/생존하였다고 판별하며, 이를 기반으로 플랫폼의 생존 영역을 표시하면 그림 6(b)와 같다. 유인체의 방사패턴은 end-fire이므로 LOS 축 방향(ϕ₀=0°)과 반대 방향(ϕ₀=180°)으로 재밍 전력이 방사되기 때문에 그림 6(b)에서 볼 수 있듯이 정면과 후면에서 접근하는 탐색기에 대해 플랫폼의 생존 영역이 형성된다. 그림 6(b)는 유인체의 전력증폭이득이 15 dB일 때의 결과이며, 전력증폭이득에 따른 플랫폼의 생존 영역을 분석하면 그림 7과 같다. 유인체의 재밍에 의한 플랫폼 생존 영역을 정량화하기 위해 전체 영역과 플랫폼 생존 영역의 비(ratio)로써 재밍 효과도(jamming effectiveness)을 수치화한다. RF 탐색기의 접근 방향을 정면(ϕ₀=0～45°), 측면(ϕ₀=45～135°), 후면(ϕ₀=135～180°)으로 나누어 각 영역에서 유인체의 전력증폭이득에 따른 재밍 효과도를 계산하면 그림 8과 같다. 정면과 후면에 접근하는 탐색기에 대해 20 dB의 전력증폭이득으로 68 %의 재밍 실효성을 확보할 수 있음을 확인할 수 있으며, 전력증폭이득이 증가함에 따라 재밍 효과도는 점진적으로 증가한다. 25 dB의 증폭이득 시 대략 70 %의 재밍 효과도를 도출해낼 수 있다. 측면에 접근하는 RF 탐색기에 대한 재밍 효과도의 변화는 미미하며, 이는 유인체의 빔 패턴이 end-fire이므로 측면으로 방사되는 에너지의 변화가 작기 때문이다. Broad-side 빔 패턴을 갖는 유인체의 전력증폭 이득에 따른 재밍 효과도를 나타내면 그림 9와 같다. 주엽의 방향인 측면으로 재밍 전력이 가장 크게 전달됨에도 불구하고, 옆면에서 접근하는 미사일에 대한 재밍 효과가 정면/측면에서 접근하는 미사일에 대한 재밍 효과보다 떨어지며, amp gain이 15 dB일 때 재밍 효과도가 대략 15 % 더 낮은 것을 확인할 수 있다. 이를 분석하기 위해 RF 탐색기 접근 방향이 방위각 ϕ₀ 방향으로 변할 때 플랫폼의 RCS를 나타내면 그림 10과 같다. 플랫폼의 측면의 유효 반사 면적이 넓고, 이에 따라 RCS(Radar Cross Section)가 정/후면의 RCS에 비해 높기 때문에 측면으로 접근하는 탐색기에 대해 J/S 비 (jamming-to-signal ratio)가 낮다. 따라서 측면에서 접근하는 RF 탐색기에 대한 기만 효과가 정면/후면에서 접근하는 탐색기에 대한 기만 효과보다 비교적 낮게 나타난다. 다음은 RF 탐색기의 초기 접근 거리에 대해 플랫폼 생존성을 분석하면 그림 11과 같다. 플랫폼은 선회비행(2 g)하며 속도는 0.8 Mach(시나리오 1)와 0.4 Mach(시나리오 2)일 때의 결과 비교를 나타내며 플랫폼 기동 속도가 생존성에 미치는 영향을 분석한다.

그림 6. | Fig. 6. RF 탐색기의 접근 위치에 따른 miss distance 및 플랫폼 생존 영역 (시나리오 1) | Miss distance and platform survival area for various RF seeker approaching locations (scenario 1).

Download Original Figure

그림 7. | Fig. 7. 유인체 전력증폭이득에 따른 플랫폼 생존 영역 (시나리오 1) | Platform’s survival area with respect to power amplifier gain of decoy(scenario 1).

Download Original Figure

그림 8. | Fig. 8. 전력증폭이득에 따른 재밍 효과도(end-fire) | Jamming effectiveness of decoy for amp gain(end-fire).

Download Original Figure

그림 9. | Fig. 9. 전력증폭이득에 따른 재밍 효과도(broad-side): 시나리오 1 | Jamming effectiveness of decoy for amp gain(broad-side): scenario 1.

Download Original Figure

그림 10. | Fig. 10. RF 탐색기 접근 방향에 따른 플랫폼 RCS: 시나리오 1 | Platform’s RCS for RF seeker approaching angle: scenario 1.

Download Original Figure

그림 11. | Fig. 11. RF 탐색기 초기 접근 거리 및 플랫폼 속도에 따른 플랫폼 생존성 | Platform survivability for initial RF seeker approaching range and platform velocity.

Download Original Figure

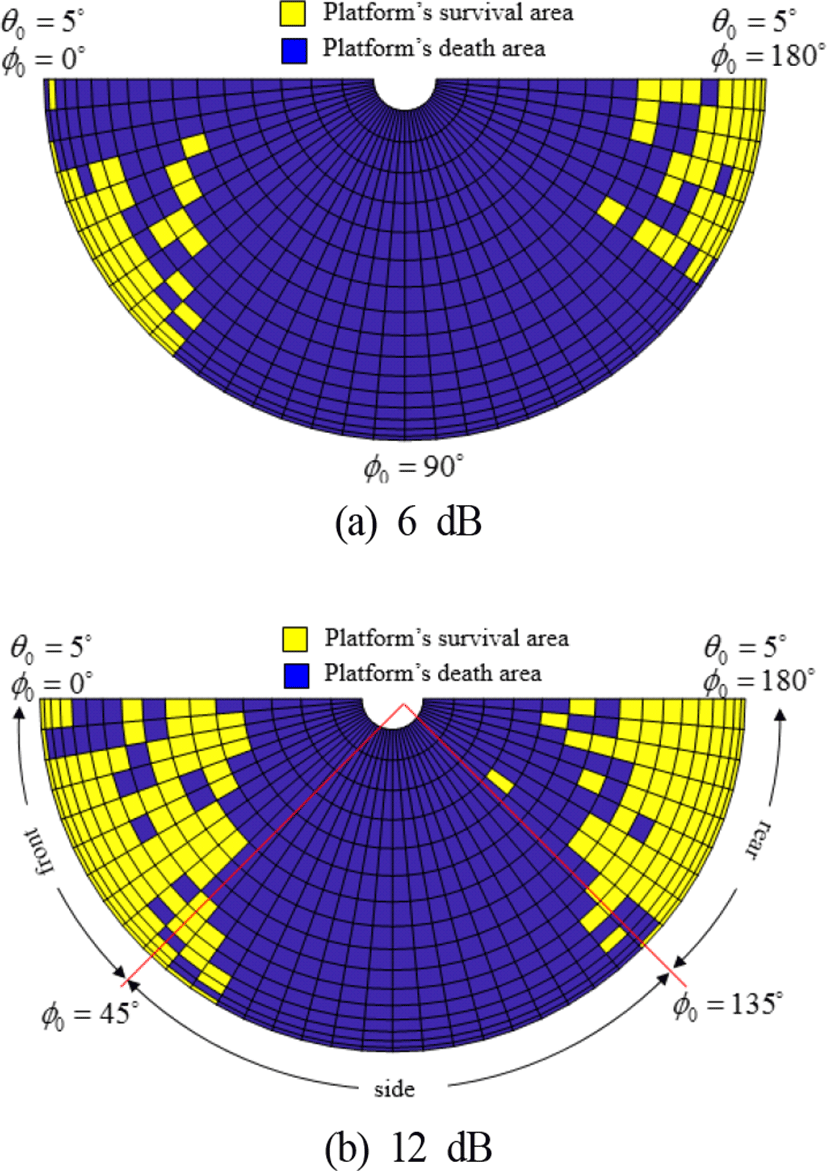
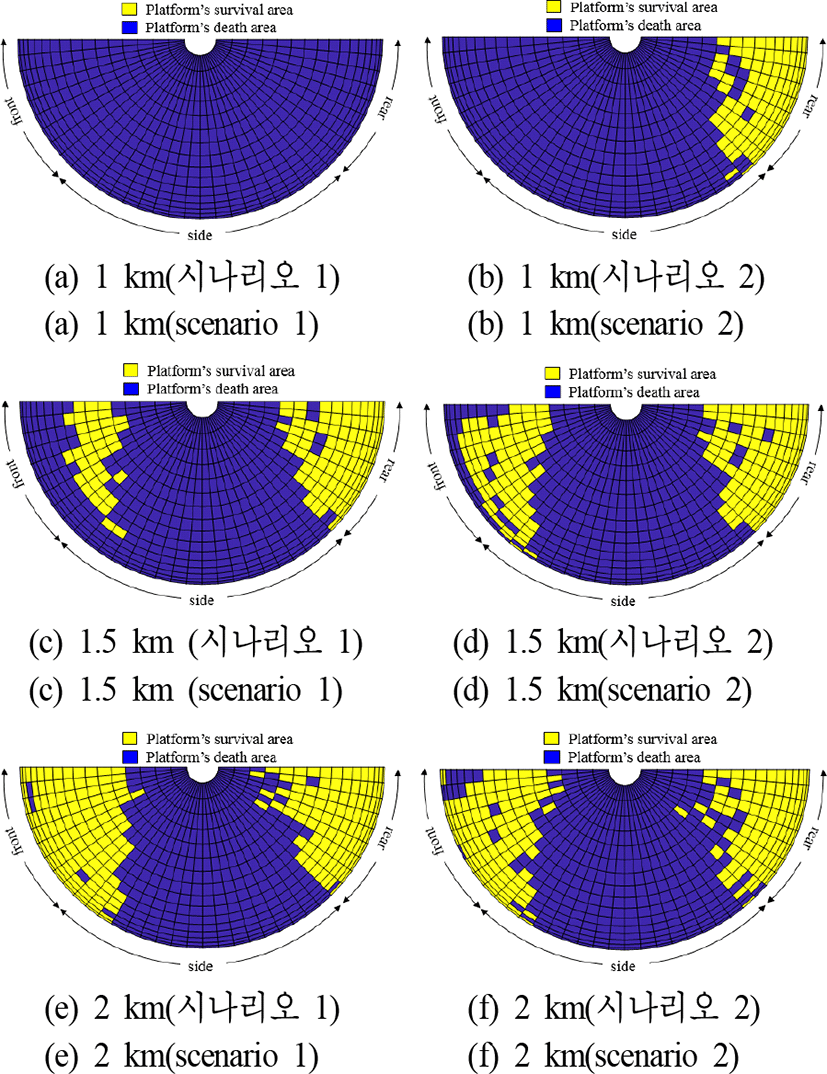
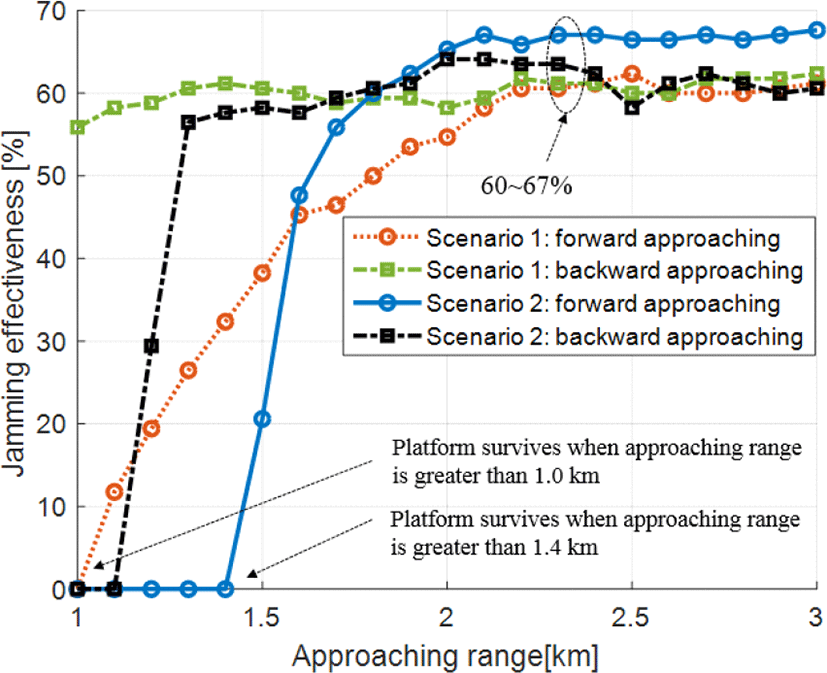
탐색기 접근거리 1 km에서 플랫폼이 0.4 Mach로 기동하는 경우, 플랫폼의 생존영역은 존재하지 않으며 0.8 Mach로 기동하는 경우, 후면 접근 탐색기에 대해 접근 영역에 대해 플랫폼의 생존성이 존재한다. 탐색기의 초기 접근 거리가 증가함에 따라 플랫폼의 생존성이 증가하는 것을 확인할 수 있다. 이를 자세히 분석하기 위해 탐색기 초기 접근 거리에 대한 재밍 효과도를 분석하면 그림 12와 같다. 0.8 Mach의 기동으로 정면 1.0 km 이상 거리에서 접근하는 탐색기에 대해 플랫폼 생존성이 보장되며 0.4 Mach 기동으로는 1.4 km 이상 거리에서 접근하는 탐색기에 대해 플랫폼의 생존성이 보장된다. 2 km 이상에서 접근하는 탐색기에 대해서는 정/후면 60～67 %의 재밍 효과도로 수렴한다. 이는 플랫폼과 유인체의 이격 거리로부터 기인한다. 플랫폼이 0.4 Mach로 기동하는 경우 두 물체의 격리 거리가 0.8 Mach로 기동하는 경우에 비해 느리게 증가한다. 0.4 Mach 기동 시 탐색기 접근거리 1.4 km부터 격리 거리가 근접신관거리인 20 m 이상이 되고 0.8 Mach 기동 시에는 1 km 탐색기 접근거리에 대해 20 m 이상이 되며, 이는 그림 12에 나타난 정면 접근 탐색기접근거리에 대한 플랫폼 생존 시작 지점과 일치한다. 즉, 탐색기에 대한 기만이 효과적으로 이루어져 탐색기가 유인체 방향으로 유도되어도 플랫폼과의 격리 거리가 충분히 확보되지 못하여 플랫폼이 탐색기의 근접신관거리 내에 위치하여 생존성이 보장되지 않는다. 따라서 플랫폼은 탐색기가 2 km 이하로 접근하기 이전에 미리 유인체를 사출하여 이격 시간을 확보하여야 생존성을 증대시킬 수 있다.

그림 12. | Fig. 12. RF 탐색기 초기 접근 거리에 따른 재밍 효과도 (시나리오 1 vs 시나리오 2) | Jamming effectiveness for initial RF seeker approaching range (scenario 1 vs scenario 2).

Download Original Figure

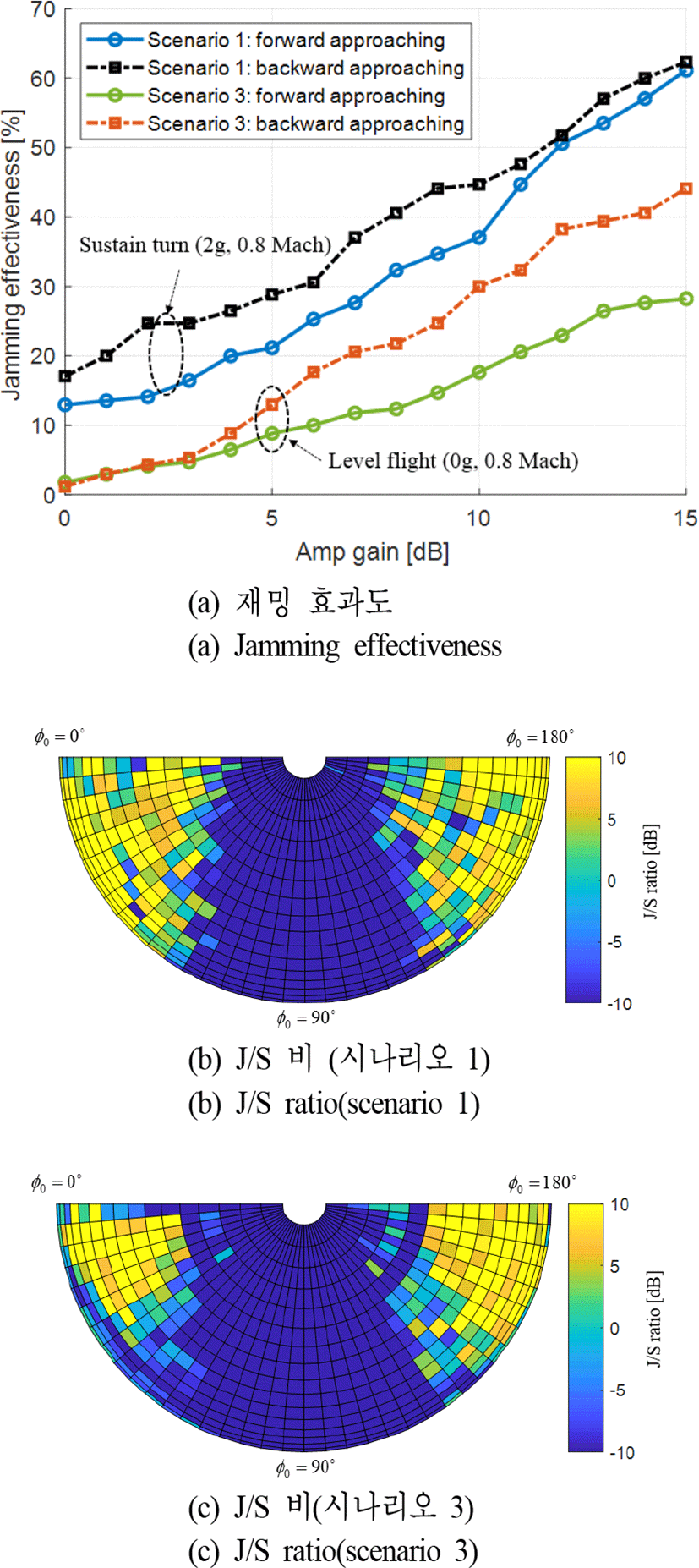
플랫폼의 기동은 탐색기의 유도에 영향을 미치는 요인 중 하나이다^[9]. 따라서 플랫폼 기동이 플랫폼 생존영역에 미치는 영향을 분석하며 이를 위해 표 1의 선회비행(시나리오 1)과 직선비행(시나리오 3)를 고려한다. 유인체의 빔 패턴은 end-fire이고 안테나 이득은 10 dB이며 RF 탐색기는 3 km의 거리에서 전 방향에서 접근하며 정/후면에서 전력증폭이득에 따른 재밍 효과도를 나타내면 그림 13(a)와 같다. 플랫폼이 선회 비행하는 시나리오의 결과가 직선비행 시나리오의 결과에 비해 정면 접근 탐색기에 대해 대략 15～20 %, 후면 접근 탐색기에 대해 10～15 % 더 높은 재밍 효과도를 갖는다. 이는 선회비행을 하는 경우 직선비행을 하는 경우에 비해 탐색기에서 관측되는 플랫폼 RCS를 낮추어 높은 J/S 비를 이끌어 낼 수 있기 때문이다(그림 13(b), (c)).

그림 13. | Fig. 13. 플랫폼 선회비행 및 직선비행 시 유인체 증폭 이득에 따른 재밍 효과도 (시나리오 1 vs 시나리오 3) | Jamming effectiveness for amplifier gain of active decoy when platform follows level flight or sustain turn maneuvering(scenario 1 vs scenario 3).

Download Original Figure

Ⅴ. 결론 및 향후 계획

본 논문에서는 PN 유도 기반 능동 RF 탐색기의 조우 시나리오에서 반복형 능동 유인체의 재밍/기만 효과에 의한 공중 플랫폼의 생존성을 분석하였다. 플랫폼의 기동, 유인체의 RF 제원(spec), 탐색기의 접근 거리 및 방향 등 여러 다른 조건의 시나리오에서 플랫폼에 대한 탐색기의 miss distance를 계산하였고 이를 근접신관거리와 비교하여 플랫폼의 생존 여부를 판별하였다. 몇몇 조우 시나리오에서 플랫폼의 생존영역을 기반으로 정/측/후면에서 접근하는 탐색기에 대한 플랫폼의 생존영역을 도출하였으며 이에 대한 원인 분석을 수행하였다. 유인체가 End-fire 빔 패턴으로 전파를 방사할 때 정/후면 접근하는 RF 탐색기에 대해 높은 기만 효과를 분석하였다. 또한 동일한 안테나 이득을 갖는 조건하에서 유인체가 Broad-side 빔 패턴으로 전파를 방사할 때의 기만효과를 분석한 결과 End-fire의 빔이 Broad-side 빔보다 측면에서 접근하는 RF 탐색기에 대한 높은 기만 효과가 높음을 확인할 수 있었다. 이는 플랫폼의 측면의 유효 반사 면적이 넓어 RCS가 크고 이에 따라 탐색기를 기만하기 위해 더 많은 재밍 전력이 요구되었기 때문이다. 플랫폼이 선회 비행하는 경우 플랫폼의 속도(0.4 Mach vs 0.8 Mach)가 생존성에 미치는 영향을 분석한 결과 플랫폼의 속도가 빠를수록 근거리에서 접근하는 탐색기에 대해 높은 생존성을 확보할 수 있었다. 이는 빠른 기동으로 플랫폼과 유인체의 격리 거리를 탐색기의 근접신관거리보다 크게 확보할 수 있었기 때문이다. 플랫폼의 속도가 느릴 경우 탐색기가 접근 거리가 가까우면 유인체에 의한 기만으로 탐색기가 유인체로 접근하더라도 근접신관거리 내에 플랫폼도 위치하기 때문에 생존성 확보가 어려움을 확인하였다. 또한 플랫폼의 기동이 플랫폼의 생존성에 미치는 영향을 분석한 결과, 플랫폼이 선회비행을 하는 경우 직선비행을 하는 경우에 비해 RCS 감소 효과로 RF 탐색기에 대해 높은 J/S 비를 확보하여 RF 탐색기에 대해 10～20% 높은 재밍 효과도를 이끌어 낼 수 있음을 확인하였다.

본 논문에서 제안된 플랫폼 생존 영역 도출 시뮬레이션을 기반으로 임의의 조우 시나리오에서 플랫폼의 생존성을 극대화하기 위한 주요 인자에 대한 분석을 수행할 수 있다. 나아가 분석된 인자들의 최적의(optimal) 조건들을 도출하여 공중 플랫폼에 접근하는 적 탐색기 레이다에 대한 효율적 기만을 도모할 수 있다.