The Journal of Korean Institute of Electc Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2017; 28(6):459-469

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2017.28.6.459

논문/REGULAR PAPERS

밀리미터파(W 밴드) FMCW SAR 기반 전방의 이동지상표적 탐지 및 위치와 속도 추정

이혁중¹^,^†, 전주환¹, 전주환^*

Forward-Looking GMTI and Estimation of Position and Velocity Based on Millimeter-Wave(W-Band) FMCW SAR

Hyukjung Lee¹^,^†, Joohwan Chun¹, Sungchan Song^*

¹한국과학기술원 전기 및 전자공학부

^*한화시스템

¹Department of Electronic Engineering, KAIST

^*Hanwha Systems

^†Corresponding Author: Hyukjung Lee (e-mail: wooa@kaist.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 12, 2016; Revised: Jun 21, 2016; Accepted: May 23, 2017

Published Online: Jun 30, 2017

요약

지상의 주력전차를 격추시키기 위한 공대지 유도미사일은 지상을 탐색하여 움직이는 표적을 탐지한 다음 위치를 추정하여 표적을 향해 나아가야 한다. 본 논문에서는 미사일이 향하는 전방의 지상을 좁은 빔 폭을 가진 빔을 기계적으로 좌우로 조향함으로써 일정한 지상구간을 탐색하며 Frequency Modulated Continuous Wave(FMCW)를 활용하여 이동하는 표적을 탐지하고 합성개구레이다(synthetic aperture radar: SAR)를 통해 위치를 추정한다. 또한 최대우도추정(maximum likelihood estimation: MLE) 기법을 통해 이동표적의 상대속도를 추정하여 레이다와 가까워지는 혹은 멀어지는 정도를 알 수 있으며 상대속도가 고려된 위상기록(phase history)을 통해 보정된 정합필터로 레이다 이미지(image)를 형성한다.

Abstract

An air-to-ground guidance missile aimed to hit a main battle tank(MBT) should detect a ground moving target and estimate the target position to guide. In this paper, we detect a front ground moving target by using FMCW(Frequency Modulated Continuous Wave) and estimate the position by forward-looking SAR(Synthetic Aperture Radar) via scanning certain front ground section by steering a beam with narrow beamwidth left to right mechanically. Also, by MLE(Maximum Likelihood Estimation), degree of how fast the target approach or recede from the radar can be figured out from the estimated radial velocity of the moving target. Subsequently, we generate a radar image via corrected matched filter from phase history including the radial velocity.

Keywords: FMCW; SAR; GMTI; MLE; Phase History; Guidance Missile

Ⅰ. 서 론

유도미사일은 목표한 표적을 보다 정밀하게 타격하여 효과적인 전투를 수행할 수 있도록 하였으며, 유도를 위한 레이다 탐색기에 고해상도 FMCW(Frequency Modulated Continuous Wave)를 활용한 가장 성공적 사례로 brimstone 미사일을 꼽을 수 있다^[1]. Brimstone 미사일은 그림 1과 같이 비행방향의 앞쪽 지면을 빔(beam) 폭이 좁은 빔으로 좌에서부터 우로 조향하며 탐색하는 방식을 가지며, 주요 목표물은 지상에서 이동하는 주력전차이다. 본 논문은 그 림 1과 같은 운용방식으로 전방의 이동표적에 대한 위치와 속도를 보다 정밀하게 추정하는 데에 목표가 있다. 유도가 정상적으로 이루어지기 위해서는 목표한 지점으로부터 약 1 km전부터 탐색하기 시작해야 하며, 낮은 고도와 작은 θ_s를 가지면 바닥의 조사되는 빔의 풋프린트(footprint)는 넓어지므로 거리해상도뿐만 아니라, 방위각의 해상도도 얻어야 표적의 정확한 위치를 알 수 있다. 본 논문에서는 거리해상도뿐 아니라 방위각 해상도도 얻기 위해 합성개구레이다(SAR: Synthetic Aperture Radar)를 사용했으며, 이는 거리 및 방위각의 해상도를 얻기 위한 대표적인 레이다 이미징 기법으로 잘 알려져 있고, FMCW를 활용한 FMCW SAR 역시 연구된 바 있다^[2]~^[6]. 그러나 합성개구레이다 이미지는 움직이는 표적에 대해서는 정확한 위치에 압축이 되지 않는 왜곡이 일어나므로 이에 대한 보상이 필요하다. 이동표적을 탐지하기 위한 기법^[1],^[7],^[8] 중 FMCW의 주파수를 상승하는 구간과 더불어 하강하는 구간을 이어 붙여서 만든 삼각펄스를 송수신한 다음 둘의 거리 측면도 간의 차이를 통해 이동표적을 탐지하는 기법^[1]을 사용하였으며 최대우도 추정을 통해 상대속도를 추정할 수 있을 뿐만 아니라, 보정된 위상기록(phase history)으로 정합필터를 재구성함으로써 영상왜곡을 보정하였다. 그 밖에도 거리 빈(range bin) 천이 현상과 거리 위상 오류보정을 수행하여 보다 정확한 위치추정을 할 수 있도록 하였다. 거리 위상 오류는 기존의 주파수 추정에 사용된 기법들 중 피크(peak) 주변의 세 값을 이용하는 방식^[9]를 통해 보정하였다. 본 논문에서는 FMCW SAR기법이 앞의 지면을 탐색하는 구조에 적용될 수 있도록 기존의 위상 기록 식의 근사를 보다 세밀하게 하였으며, 움직이는 표적을 탐지하고 상대속도를 추정함으로써 영상왜곡보정 및 지상표적을 탐지하는 일련의 과정을 모의실험을 통해 확인하였다.

그림 1. | Fig. 1. 앞의 지면을 탐색하는 구조 | Forward-looking SAR geometry.

Download Original Figure

Ⅱ. 모의실험 원시 데이터 생성

그림 1과 같이 θ_s, ϕ_s만큼 기계적으로 빔을 조향하여 비행방향의 앞쪽 지면을 탐색하며, 일정한 펄스 반복 주기마다 펄스를 송수신하여 축적한 데이터를 원시 데이터라고 한다. 그림에서 h는 레이다 탑재체의 높이, x축은 비행체의 진행방향, y축은 지면과 평행하고 진행방향에 수직한 방향, z축은 지면을 향하는 방향을 나타내며 빔이 조향되는 시선(line of sight)의 방향을 나타내는 $k → = cos θ s cos ϕ s x → + sin ϕ s y → + sin θ s cos ϕ s z →$ 와 같이 표현된다. 이때 그림 2와 같이 빔 폭 ϕ_b, θ_b에 의해 바닥에 조사되는 풋프린트의 크기가 결정되며, 모의실험 시 빔의 조향 각에 따라 빔의 안에 존재하는 표적에 의해 반사되는 신호만을 고려하였다. 따라서 본 절에서는 빔 폭에 의해 결정되는 풋 프린트 내부를 나타내는 부등식을 얻는다.

그림 2. | Fig. 2. 빔 폭과 바닥에 조사되는 풋프린트(a) 및 조사방향과 풋프린트 너비와의 관계(b) | Footprint for constant beam width(a) and relation between line of sight of radar and footprint length(b).

Download Original Figure

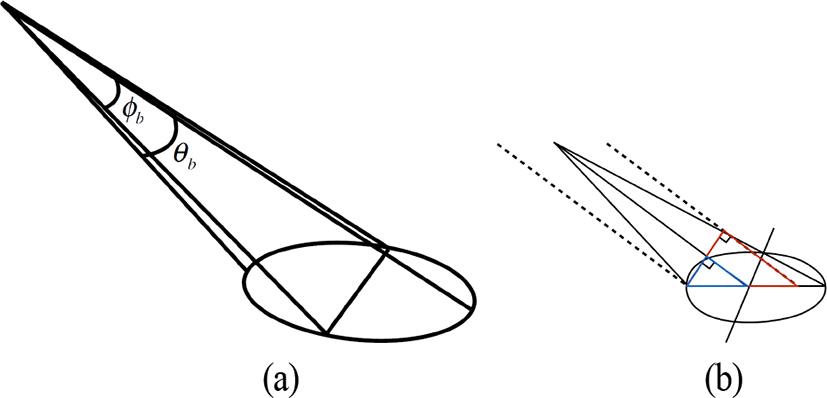
그림 2의 우측을 통해 레이다가 조사하는 시선과 평행한 보조선(점선)을 그리면 그 시선이 바닥에 닿는 지점으로부터 풋프린트의 아래 끝점과 위 끝점까지 거리가 다름을 알 수 있다. 본 논문에서는 풋프린트를 시선이 바닥에 닿는 지점을 원점으로 하여 그림 3과 같이 단축을 공유하고, 장축이 다른 두 개의 타원이 합쳐진 도형으로 가정하였다. 이 때, 기계적으로 ϕ_s만큼 조향된 x′, y′축 상에서

y ′ 2 a 2 + x ′ 2 b 2, x ′ >__0 y ′ 2 a 2 + x ′ 2 c 2, x ′ <__0

(1)

를 만족하면 그 표적은 빔 안에 존재하는 지상표적이라고 할 수 있다. 에서 a,b,c는 와 같이 θ_s, ϕ_s의 각도로 조향했을 때 두 개의 평면상에 나타나는 직각삼각형을 이용하면 다음과 같이 구해진다.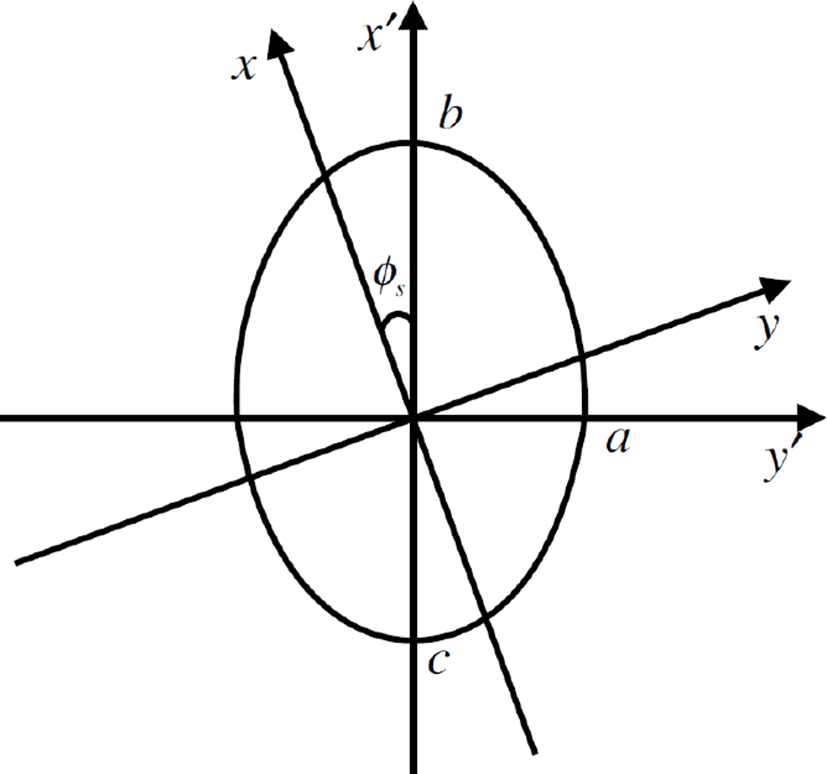

그림 3. | Fig. 3. 단축을 공유하고 장축이 서로 다른 두 개의 타원이 합쳐진 도형 및 ϕ_s만큼 회전된 축 x′, y′ | Combined ellipse in rotated axises.

Download Original Figure

그림 4. | Fig. 4. 상단 그림(a)의 첫 번째, 두 번째 평면에서 나타나는 장축 및 단축 | Major and minor axis of ellipse from 1^st, 2^nd plane in upper figure.

Download Original Figure

a = R tan ϕ b

(2)

b = h tan (φ + θ b) − h tan φ,

(3)

c = h tan φ − h tan (φ − θ b) .

(4)

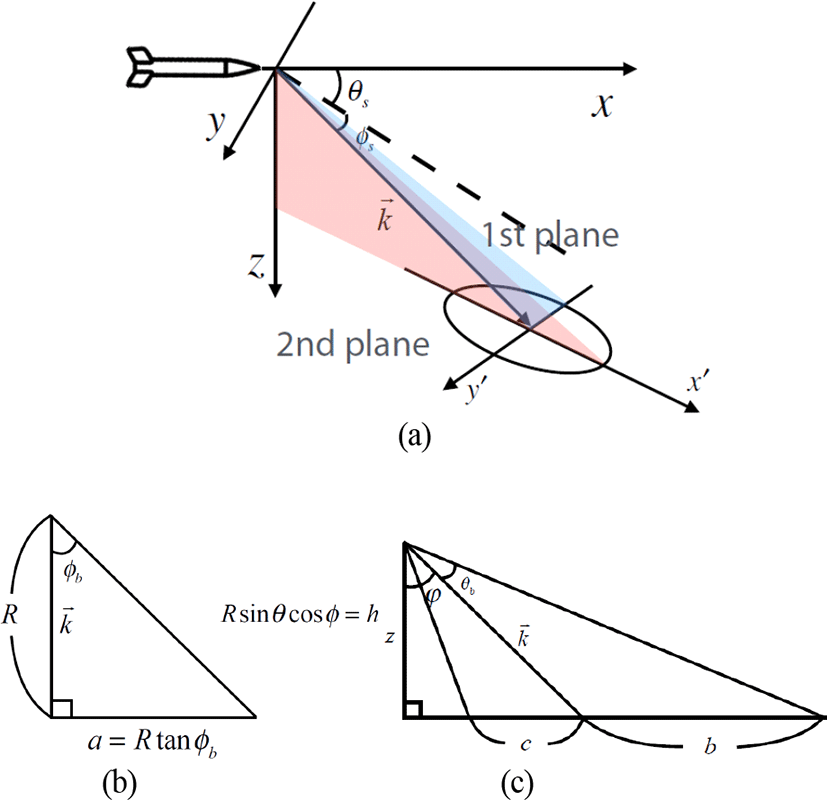
위에서 R은 데이터가 조사하는 방향으로 닿는 바닥과의 직선거리를 의미하며, φ = cos⁻¹(sinθ_scosϕ_s)와 같이 구해진다. 식 (1)의 부등식을 활용하기 위해서는 x,y 좌표평면 상에 존재하는 표적의 좌표를 원점이동 및 회전이동을 통해 가정한 타원의 중심을 원점으로 하는 x′,y′ 좌표평면으로 변환시켜야 한다. 즉, 레이다의 고각 및 방위각으로 결정되는 조향 각 θ_s,ϕ_s에 의해 정해진 중심은 (R sinϕ_s,R cosθ_s cosϕ_s)임을 이용하면 와 같이 좌표변환을 할 수 있다.

[y ′ x ′] = [cos ϕ s − sin ϕ s sin ϕ s cos ϕ s] [y − R sin ϕ s x − R cos ϕ s cos ϕ s]

(5)

Ⅲ. FMCW 신호 분석

본 논문에서 사용되는 FMCW 펄스의 파형은 그림 5와 같다. 움직이는 지상표적을 탐지하기 위해 주파수가 증가하는 구간뿐만 아니라, 감소하는 구간이 합쳐진 형태로 삼각펄스 형태를 가지며, 펄스의 폭은 1 ms, 대역폭은 300 MHz, 반송 주파수는 94 GHz로 정하였다^[1]. 펄스반복주기(pulse repetition interval)를 1 ms로 한다면 그림 5와 같은 펄스를 이어 붙여 계속해서 송신하는 것으로 이해할 수 있다. 본 절에서는 수신되는 신호를 빠른 시간(fast-time) 및 느린 시간(slow-time) 두 가지 관점으로 나눠서 분석한다. 즉, 펄스를 하나 송수신했을 때 수신된 신호를 분석하고, 펄스반복주기로 신호를 쌓았을 때 피크 값의 위상정보를 분석한다. 주파수가 하강하는 구간은 상승하는 구간 과 비슷하게 식을 유도할 수 있기 때문에 본 논문에서는 상승하는 구간에 대해서만 신호를 분석하였다.

그림 5. | Fig. 5. 본 논문에서 사용되는 FMCW 펄스의 파형 | FMCW pulse representation.

Download Original Figure

3-1 빠른 시간(Fast-Time) 분석

먼저 송신되는 FMCW 신호 s(t)는 다음과 같이 주어진다.

s (t) = exp [j (2 π f c t + π K t 2)], 0 <__t < S .

(6)

위에서 f_c는 반송 주파수, K는 주파수 증가 기울기를 의미하며, S는 증가하는 구간의 시간길이(500 us)를 의미한다. 반사율이 1인 단일의 점표적이 존재한다고 했을 때 빔이 표적을 조사했을 경우, 수신되는 신호는 τ만큼 시간지연을 가지게 된다. 따라서 수신된 신호는

s (t − τ) = exp [j (2 π f c (t − τ) + π K (t − τ) 2)], τ <__t < S + τ

(7)

와 같다. FMCW의 신호처리 특징으로 수신한 신호를 송신한 신호와 켤레복소수(conjugate) 곱을 하게 된다. 곱셈기를 통과한 신호는 다음과 같다.

s (t) s * (t − τ) = {exp [j (2 π K τ t + 2 π f c τ − π K τ 2)], τ <__t < S 0, 0 <__t < τ

(8)

이때, 레이다 탑재체의 이동속도가 빠르다면 시간지연은 더 이상 상수가 아닌 시간의 함수가 된다. 따라서 τ를 빠른 시간 t의 함수로 나타내면 다음과 같다.

τ = 2 R (t) c ≅ 2 c (R (0) + R ˙ (0) t + 12 R ¨ (0) t 2)

(9)

위에서 표적과 레이다와의 거리 R(t)를 다항함수로 표현하기 위해서 테일러급수(Taylor series)를 사용하였다.

빠른 시간의 함수로 표현된 τ를 곱셈기를 통과한 식 (8)에 대입한 다음 상대적으로 값이 작아 주파수 혹은 위상에 대한 영향이 무시할 정도로 작은 항은 1로 근사하였다. 근사한 결과는 다음과 같다.

exp [j (2 π K τ t + 2 π f c τ − π K τ 2)] ≅ exp [j (2 π f c τ 0 − π K τ 02)] ⋅ exp [j (2 π f b t − 2 π f D t)] ⋅ exp (π 4 K R ˙ (0) c t 2)

(10)

위에서 $τ 0 = 2 c R (0), f D = − 2 R ˙ (0) λ, f b = K τ 0$ 를 의미한다. t²에 의한 항을 보상한다면 위의 결과는 f_b−f_D인 단일주파수를 가지는 정현파 신호가 된다. 보상하는 과정은 도플러 주파수를 보상하는 절에서 자세히 다룬다. 정현파 신호를 푸리에 변환(Fourier transform)한 결과 중 피크 값의 위상 값은 0이므로 $exp [j (2 π f c τ 0 − π K τ 02)]$ 항이 피크의 위상 값이 된다.

3-2 느린 시간(Slow-Time) 분석

기존의 합성개구레이다기법과 마찬가지로 동일한 펄스를 여러 번 송수신하여 거리 측면도 데이터를 모음으로써 같은 표적으로부터 수신된 위상기록을 얻을 수 있고, 이는 움직이는 탑재체의 운동에 의한 상대거리 변화를 펄스반복주기로 샘플링한 것과 같다. 이 위상기록은 표적의 위치정보를 담고 있기 때문에 정합필터를 이용하면 진행방향으로의 위치를 구별해 낼 수 있다^[10],^[11]. FMCW의 곱셈기를 통과한 신호를 푸리에 변환한 결과 중 피크 값의 위상은 다음과 같다.

exp [j (2 π f c τ 0 − π K τ 02)] exp [j (2 π (f b − f D) t s t a r t)]

(11)

위에서 t_start는 빠른 시간상에서 샘플링(sampling)하기 시작한 시간을 의미하며 레이다가 조사하는 바닥 중 거리가 가장 먼 곳을 기준으로 샘플링해야 곱셈기를 통과한 신호에 모든 표적에 대한 정보가 담겨 있으므로 가장 먼 위치의 거리 R_max를 기준으로 $t s t a r t = 2 R max c$ 와 같 이 정한다. 이때 느린 시간(slow-time) 상에서는 펄스반복주기마다 위상의 값은 변하게 된다. 즉, τ₀ 및 f_b, f_D의 값도 느린 시간 t_s의 함수가 된다. 빠른 시간 분석의 방법과 비슷하게 테일러급수를 이용하면

τ 0 (t s) = 2 R (t s) c ≅ 2 c (R (0) + R ˙ (0) t s + 12 R ¨ (0) t s 2)

(12)

f b (t s) = K τ 0 (t s)

(13)

f D (t s) = − 2 (R ˙ (0) + R ¨ (0) t s) λ

(14)

와 같이 표현된다. R(0)는 거리 압축을 통해, $R ˙ (0)$ 은 빔의 중심 도플러를 통해 알 수 있으며, $R ¨ (0) = V 2 R 2 (0) − R 2 (0) R 2 (0)$ 와 같이 계산된다. 결론적으로, 식 (12)～(14)를 식 (11)에 대입하면 피크의 위상기록을 얻을 수 있으며 이 위상기록을 통해 진행방향으로의 압축 즉, 합성개구레이다기법의 적용이 가능하다.

Ⅳ. 거리 빈 천이 현상 및 위상 오류 보정

곱셈기를 통과한 신호는 f_b−f_D의 주파수를 가지는 정현파 신호인데, 표적과 레이다 간의 거리정보는 f_b에 담겨 있기 때문에 f_D만큼 보상해 줘야 거리를 제대로 측정할 수 있다. 즉, f_D의 영향이 주파수 해상도 Δf보다 크면 보정이 필요하며

Δ f <__f D max

(15)

의 조건을 만족하면 보상과정이 필요하다. 위에서 f_Dmax는 레이다의 빔 폭이 허락하는 범위 안에서 가장 큰 도플러 주파수의 크기를 의미한다. 또한 본 논문에서는 펄스 폭 만큼의 펄스반복주기를 가지고 연속해서 FMCW 신호를 송수신하기 때문에, 레이다 탑재체의 속도가 빠르다면 펄스반복주기마다 거리 빈의 위치가 밀리는 거리 빈 천이 현상이 나타난다. 빈 천이 현상은 다음과 같은 조건 하에서 발생한다.

Δ R <__V r ⋅ P R I ⋅ N o P

(16)

위에서 ΔR은 거리 분해능을 나타내며, V_r은 표적과 레이다 간의 상대속도, NoP는 표적이 레이다 빔에 조사되는 동안 모이는 펄스의 수를 의미하고, 빔의 회전속도, 빔 폭, 탑재체의 속도에 의해 결정된다^[12]. 도플러 주파수 보상방법은 다음과 같다. 레이다의 빔 폭이 충분히 작고, 빔의 중심에서 나타나는 도플러 주파수와의 차이의 최댓값이 Δf보다 작다면 거리측정에 주는 오차가 최대 1빈이기 때문에 크지 않다고 보고, 다음과 같은 중심 도플러로 보상해준다.

f D C = 2 V cos θ s cos ϕ s λ

(17)

위에서 θ_s, ϕ_s는 빔의 조향 각을 의미하며, V는 레이다 탑재체의 진행방향으로의 속도를 의미한다. 본 논문에서 사용하는 파라미터에 의하면 f_D−f_DC ≦ Δf를 만족한다. 다음으로 거리 빈 천이 현상은 상대속도에 의해 벗어나는 빈의 정도를 k번째 펄스에 대해서 다음과 같이 계산할 수 있다.

N o f s h i f t = V r (k − 1) P R I Δ R

(18)

위에서 V_r=−V cosθ_s cosϕ_s로 표적의 위치에 따라 상대적인 속도는 다르기 때문에 도플러 주파수를 보상할 때와 마찬가지로 중심도플러에 의해 나타나는 상대속도를 사용하였다. 벗어나는 빈 수의 소수점은 반올림하여 처리한다.

단일주파수신호의 주파수를 DFT(Discrete Fourier Transform)를 활용하여 찾고자 할 때 피크 지점이 정확하지 않으면 위상오차가 발생한다. 그림 6에서 신호가 가진 실제 주파수를 나타내는 m은 정수가 아니지만, DFT 인덱스(index) k는 정수이므로 실제 피크지점과 오차가 존재한다.

그림 6. | Fig. 6. DFT(Discrete Fourier Transform)(막대)와 DTFT 결과(실선) 및 실제 피크지점 m과 DFT했을 때의 피크지점 k | Comparison of DFT and DTFT respect to peak position.

Download Original Figure

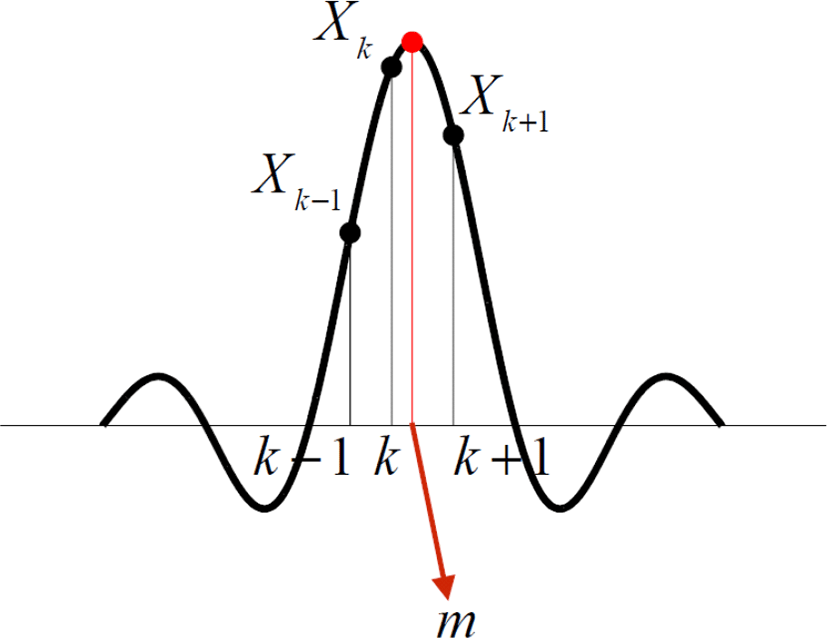
이 때 X_k가 가지는 위상은 $exp (− j π (k N − m N) (N − 1))$ 과 같고, N은 시간 축에서 신호를 샘플링한 개수를 의미한다. 이 때 m은 DFT 결과의 피크를 포함한 세 개의 값을 이용하여 다음과 같이 계산된다^[9].

m = k − Re [X k + 1 − X k − 1 2 X k − X k − 1 − X k + 1]

(19)

따라서 위상 오류 보정은 DFT 결과의 피크 값에 대해 다음과 같은 처리를 해줌으로써 수행한다.

X k ⋅ exp (j π (k − m) N − 1 N) .

(20)

Ⅴ. 움직이는 지상표적 탐지

FMCW의 증가하는 구간과 더불어 감소하는 구간을 이 용하여 지상에 움직이는 표적이 있는지 탐지할 수 있다. 움직이는 표적에 의한 도플러 주파수를 $f D t = − 2 V t r λ$ (V_tr 은 표적의 움직임으로 인한 레이다와 표적의 상대속도) 라고 하면 식 (10)에서 f_b−f_D는 f_b−f_D−f_Dt와 같이 표적에 의한 도플러 주파수만큼 감소하게 된다. 감소하는 구간의 수신신호 역시 같은 방식으로 이끌어 내면 주파수는 f_b+f_D+f_Dt와 같이 증가하게 된다. 이때 레이다 탑재체의 속도에 의해 발생한 도플러 f_D는 f_DC로 보상하면 지상표적이 존재할 때만 속도에 의해서 증가, 감소 구간의 거리 빈이 밀리게 된다. 예를 들어 본 논문에서 사용한 파라미터에 따르면 V_tr = 50 km/h인 경우 f_Dt ≅ −8.7 kHz로 Δf ≅ 2 kHz일 때 거리 축으로 4개의 빈이 오른쪽으로 밀리게 된다. 감소하는 구간의 데이터는 왼쪽으로 밀리므로 각각의 피크위치가 여덟 빈 차이가 나타나게 된다. f_D−f_DC에 의한 오차는 1빈 이내이므로 f_Dt = 0인 경우, 피크 값의 거리 빈 최대 차이는 1빈이기 때문에 탐지 문턱 값은 2빈으로 정하였다.

움직이는 표적이 존재하면 식 (11)의 위상기록에도 영향을 미치므로 표적의 상대속도를 고려해야 레이다 이미지 압축이 정상적으로 이뤄진다. 상승과 하강 구간의 거리 축 데이터의 피크 값의 거리로 대략적인 상대속도를 알아낸 다음 최대우도 추정기법으로 상세한 값을 추정하여 레이다 이미지를 보정한다. 그 이유는 최대우도 추정기법에서는 상대속도의 값에 따라 피크 값이 다수 발생하는 모호성이 있기 때문이다. 최대화해야 하는 우도함수는 다음과 같다.

1 π det (R) exp [(z − b a (V t r)) H R − 1 (z − b a (V t r))]

(21)

위에서 (·)^H는 켤레복소수 전치를 의미하고, z는 펄스를 NoP개 송수신했을 때 거리 축의 피크 값들을 벡터로 쌓은 측정값(measurement) z=ba(V_tr)+n이며, n은 잡음을, R은 그 잡음의 공분산 행렬을 나타낸다. 위는 잘 알려진 우도함수의 형태로 b는 신호의 크기로써 nuisance 파라미터이므로 우도함수를 일반화하기 위해 $b^= a H (V t r) R − 1 z a H (V t r) R − 1 a (V t r)$ 와 같이 우도함수의 정류점 값으로 추정한다. $b^$ 을 식 (21)에 대입한 다음, 동등하게 최대화해야 하는 우도함수는 다음과 같이 정리된다.

L (z | V t r) = | a H (V t r) R − 1 z | 2 a H (V t r) R − 1 a (V t r)

(22)

위에서

a (V t r) = exp [j (2 π f c τ 0 (t s, V t r) − π K τ 02 (t s, V t r))] . exp [j (2 π (f b (t s, V t r) − f D (t s, V t r)) t * t)]

(23)

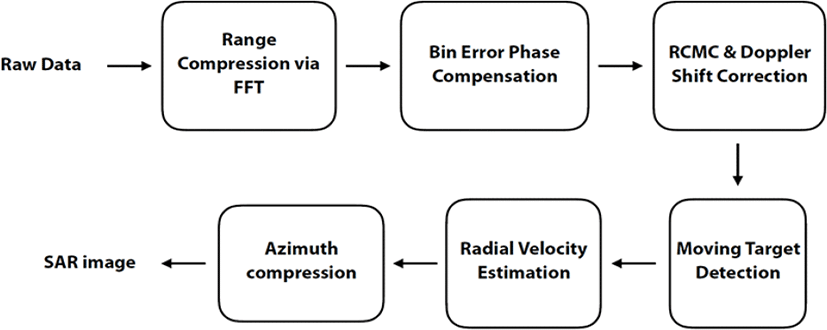
로 상대속도가 포함된 위상기록을 벡터형태로 나타낸 것이다. 위에서

τ 0 (t s) = 2 R (t s) c ≅ 2 c (R (0) + (R ˙ (0) + V t r) t s + 12 R ¨ (0) t s 2)

(24)

f b (t s, V t r) = K τ 0 (t s, V t r)

(25)

f D (t s, V t r) = − 2 ((R ˙ (0) + V t r) + R ¨ (0) t s) λ

(26)

을 나타낸다.

본 논문에서 제안하는 전체적인 기법을 종합하여 그림 7과 같은 신호처리 블록도를 따라 보정된 SAR 이미지 및 상대속도를 얻을 수 있다. 먼저 원시 데이터를 FMCW 신호를 송수신함으로써 얻은 다음 FFT를 이용해 거리압축을 수행한 후 위상오류를 보정하고, 레이다 탑재체의 이동에 의한 거리 빈 천이 현상 및 도플러 현상에 의한 도플러 주파수 천이를 보정한다. 이와 같은 과정을 거치면 보다 개선된 거리추정 결과를 얻게 된다. FMCW의 상승 및 하강 펄스에 의해 얻어낸 거리 측면도의 차이를 통해 움직이는 표적의 유무를 가려내고, 여러 번 쏘아 받아낸 진행방향 축으로의 위상기록 정보로 MLE 기법을 적용함으로써 움직이는 표적의 상대속도를 추정할 수 있다. 움직이는 표적은 움직이지 않은 표적과 다른 위상기록을 가지기 때문에 상대속도를 고려한 보정된 진행방향 압축을 통해 왜곡이 보상된 SAR 이미지를 최종적으로 얻을 수 있다. 즉, 본 논문에서 목표한 표적의 위치 및 상대속도에 대한 추정이 완료된다.

그림 7. | Fig. 7. 본 논문이 제안하는 전체적인 신호처리 블록도 | Block diagram of overall process.

Download Original Figure

Ⅵ. 모의실험 결과

모의실험에 쓰인 파라미터는 표 1과 같다^[1]. 단일 점표적에 대해 모의실험을 수행하기 위해 레이다가 (0,0,0)에 존재한다고 했을 때 (878, −130, −h)[m]의 위치에 반사율이 1인 지상의 점표적이 있다고 가정하였으며 빔 폭 θ_b, ϕ_b를 가지고 기계적 조향으로 −9°부터 9°까지 $ϕ ˙ s$ 의 속도로 200 ms 동안 조사되는 빔의 풋프린트를 16 ms간격으로 그림 8에 나타냈다. 그림 8과 같이 본 논문에 서 제안하는 레이다는 레이다로부터 약 800 m 떨어진 앞쪽 지면 중 330×300 m에 해당하는 지역을 탐색하는 것을 알 수 있으며, 합성개구레이다 기법과 움직이는 지상표적탐지 알고리즘을 통해 움직이는 표적의 위치와 속도를 추정하는 데에 목표가 있다.

표 1. | Table 1. 모의실험 파라미터 | Simulation parameters.

Parameters	Values
Height of the vahicle h	50 m
Steering angle θ_s	3.56°
Elevation beamwidth θ_b	1.4°
Azimuth beamwidth ϕ_b	1.4°
Velocity of the vehicle ν	450 m/s
Sampling frequency f_s	10 MHz
PRI	1 ms
Bandwidth	300 MHz
Range resolution	0.5304 m

Download Excel Table

그림 8. | Fig. 8. 점표적과 200 ms 동안의 빔 풋프린트 | Point target and footprints during 200 ms.

Download Original Figure

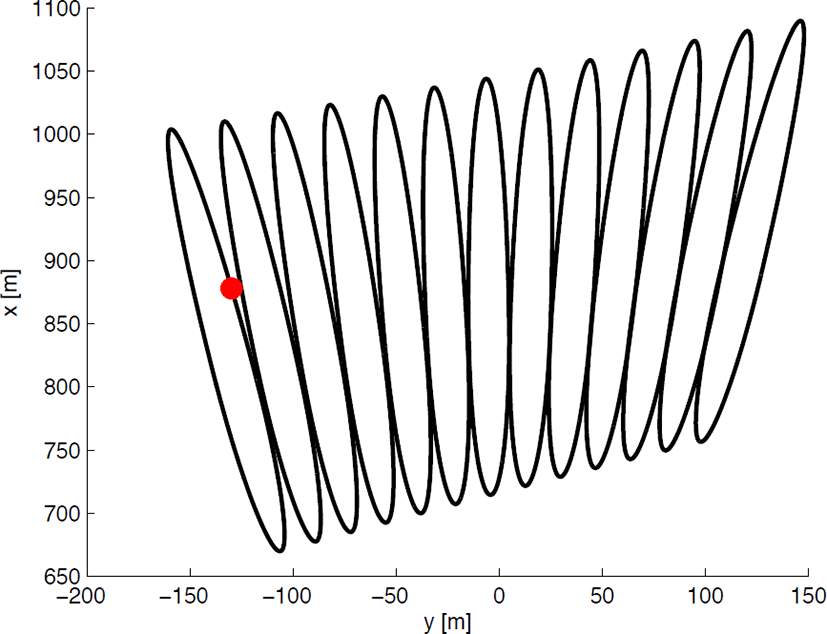
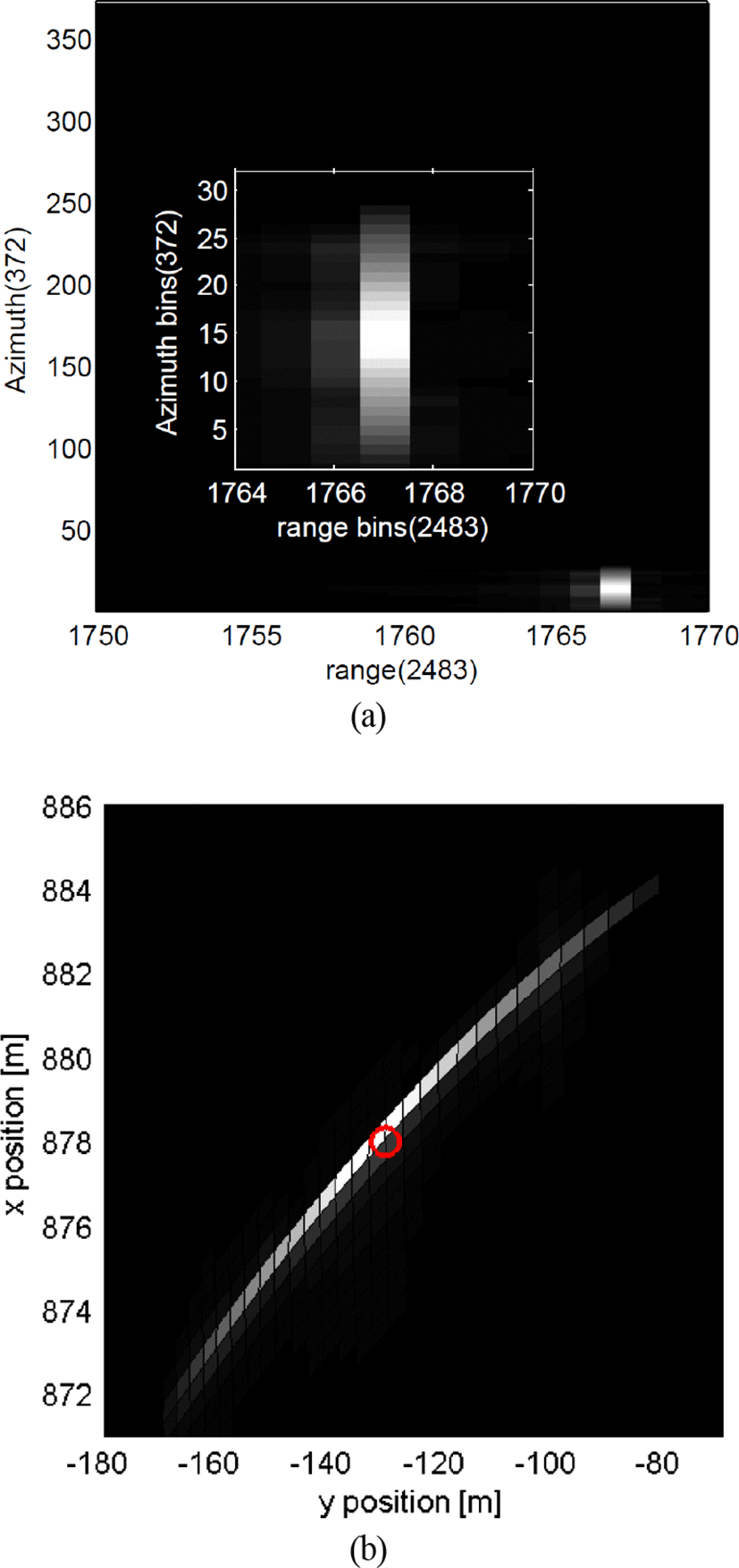
그림 9는 FMCW의 증가구간을 송수신하여 곱셈기를 통과한 원시 데이터에 FFT(Fast Fourier Transform)를 수행한 다음, 거리 빈 천이현상 및 위상오류를 보정한 후 절대 값 크기에 비례하는 밝기로 나타낸 거리압축 결과이다. 세로축은 펄스 반복 주기로 데이터를 쌓은 개수를 나타내며, 가로 축은 거리 빈의 수를 의미한다. 또한 그림 중심에 확대된 모습도 같이 나타냈다. 그림 8과 같이 좁은 빔 폭을 가진 빔을 회전시키면 표적을 13 ms 동안만 조사하게 되므로 어느 정도 표적간의 구별이 가능하지만, 13개의 펄스 내에서는 구분이 되지 않는 것을 볼 수 있다.

또한 피크가 나타난 1767빈 수에 의해 계산된 거리는 889.00 m이고, 실제 거리 $8782 + 1302 + 502 = 888.98 m$ 임 을 통해 오차가 거리 빈 내로 들어오는 것을 확인할 수 있다.

그림 9. | Fig. 9. 거리압축 결과 | Results of range compression.

Download Original Figure

그림 10은 그림 9에서 진행방향 압축을 한 결과이다. 정합필터를 적용했기 때문에 길이가 길어졌지만 그림 9와는 달리 압축된 것을 볼 수 있다. 위치 정보를 제대로 추정했는지를 알기 위하여 값을 x,y축에 나타내었고, 마찬가지로 밝은 부분이 크기가 큰 부분이다. 원으로 표시된 부분이 실제 위치이며, 이미지 상에서 피크의 x, y 위치는 (878.06, −130.04)으로 나타났다.

그림 10. | Fig. 10. 진행방향압축 결과(a) 및 x, y 좌표로 나타낸 그림(b) | Azimuth compression result(a) and image on x, y axis(b).

Download Original Figure

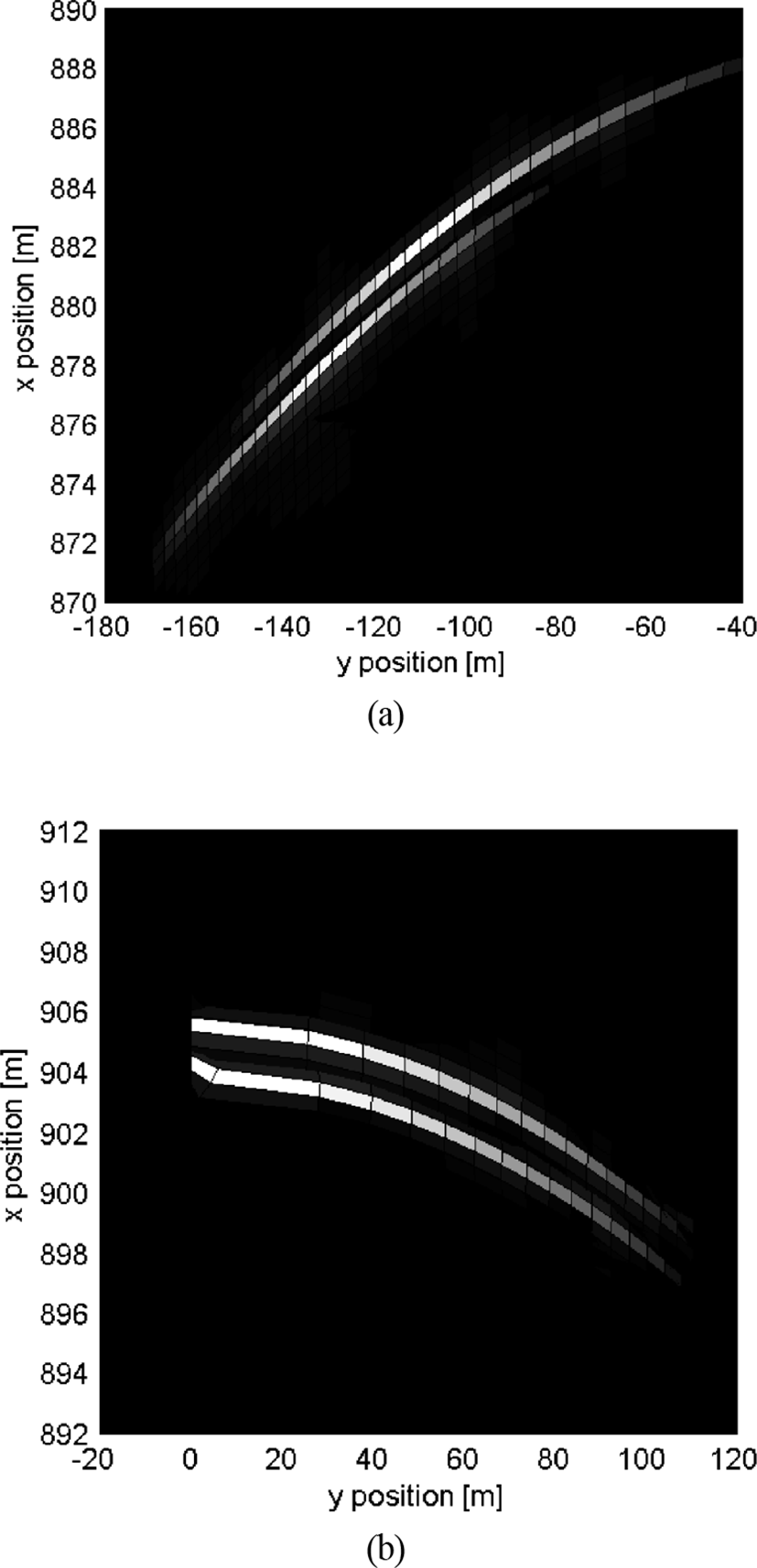
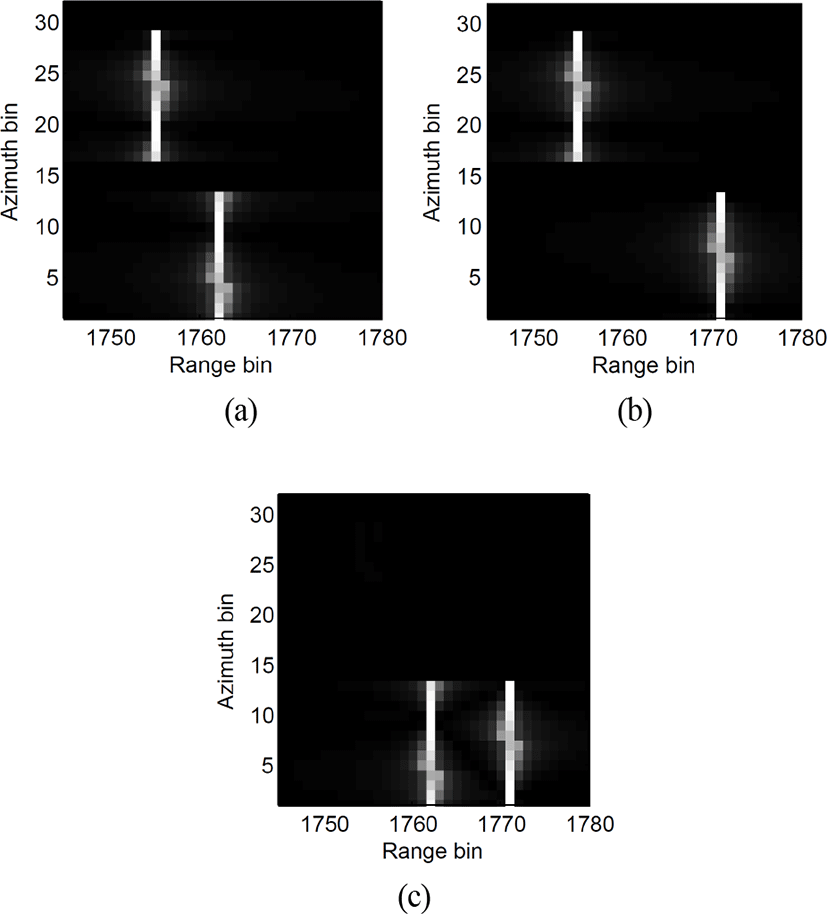
단일의 표적이 아닌 경우에는 측정치에 다수의 정보가 섞여져 있게 된다. 단일의 표적이 아닌 경우에도 위치 추정이 이루어지는지 그림 11에서 확인하였다. 먼저 (898, −130) 및 (882, −107)에 존재할 때 이미지 상 피크는 (878.06, −130.04), (882.26, −107.05)에 나타났으며, 거리 방향에 비해서 방위각 방향으로는 분해능이 낮은 것을 확인할 수 있다. 중심에 표적이 존재할 때는 이론적으로 합성개구레 이다의 방위각 방향 분해가 불가능해지므로 피크의 위치는 (903.60, 4.46), (904.87, 25.73)로 실제 위치 (903.5, 4), (905, 25.5)와 비슷한 위치로 나타났지만, 이미지 상에서는 방위각 방향으로 구분이 거의 되지 않는 모습을 보였다. 다만 신호가 몇 번째에 수신되었는가를 통해 표적의 좌우 위치는 알 수 있으므로 우측에만 이미지가 나타난 것을 확인할 수 있다.

그림 11. | Fig. 11. 왼쪽 부근에 두 개의 표적이 있는 경우(a) 및 중심 부근에 두 개의 표적이 있는 경우(b) 합성개구레이다 이미지를 x, y 좌표로 나타낸 그림 | Image of two targets on left side(a) and on center (b) on x, y axis.

Download Original Figure

FMCW의 상승 구간으로부터 얻은 거리압축 결과와 하 강 구간으로부터 얻은 거리압축 결과로부터 움직이는 표적을 탐지할 수 있다. (878, 7−130), (882, −107)에 위치하는 두 개의 표적 중 (878, −130)에 존재하는 표적만 상대속도 V_tr = −50 km/h로 레이다로 다가오고 있을 때 상승구간 데이터 및 하강구간 데이터를 거리압축 한 결과와 두 결과의 차의 절대 값을 그림 12에 나타냈다. 그림 상 위쪽에 있는 표적은 움직이지 않고, 아래쪽에 있는 표적은 움직인다. 따라서 아래 쪽 표적만 f_Dt에 의해 좌우로 4빈씩 밀려있는 것을 확인할 수 있으며 차를 구하면 움직이지 않는 표적에 대한 거리 측면도는 삭제된 것을 확인할 수 있다. 문턱 값 2빈을 적용하면 아래 표적은 피크 간 거리가 8빈이므로 이동표적이라고 탐지 가능하며, 상승구간 데이터 중 움직이는 표적의 피크지점들을 측정값으로 하여 최대우도 추정을 수행한다.

최대우도측정 결과는 그림 13과 같다. 실제 상대 속도 −50 km/h와는 약간의 오차를 가지고, $V^t r = − 49.75 km/h$ 로 추정되었다. f_D를 보정할 때 f_DC를 이용하므로 오류 로 남는 f_D−f_DC에 의한 위상변화가 추정결과에 오류를 야기한다. 추정된 V_tr로 보정된 위상기록을 얻을 수 있으며, 이를 통해 보상된 진행방향으로의 압축을 할 수 있다. 멈춰있는 표적에 대해서는 기존과 같은 위상기록을 사용하여 이미지를 얻으면 그림 11의 상단과 동일한 결과를 얻게 된다.

그림 12. | Fig. 12. 상승 구간 데이터의 거리 압축(a), 하강 구간 데이터의 거리 압축(b) 및 차의 결과(c) | Range compression for up sweep(a) and down sweep (b) and result of subtraction(c).

Download Original Figure

그림 13. | Fig. 13. 최대우도추정 결과 | Result of maximum likelihood estimation.

Download Original Figure

Ⅶ. 결 론

본 논문에서는 레이다가 전방의 지면을 탐색하는 상황에서 지상의 이동표적을 탐지하고, 위치와 속도를 추정하는 과정을 모의실험을 통해 보였다. 이동 표적과 정지 표적을 구별하기 위해 FMCW의 상승 및 하강 구간으로부터 얻은 데이터의 차를 이용했으며, 위치를 추정하기 위해 최대우도함수 기법을 적용하였다. 또한 비행체의 속도에 의한 빈 천이 현상 및 거리 위상 오류를 보정하였다. 이동표적을 탐지하기 위한 문턱 값 및 합성개구레이다를 수행할 때 적분시간(integration time)을 정하는 알고리즘이 앞으로 연구되어야 한다.

References

[1].

Brooker, Graham, Alan T. Brooker, Introduction to Sensors for Ranging and Imaging, SciTech Pub. Incorporated, 2009.

[2].

Meta, Adriano, Signal Processing of FMCW Synthetic Aperture Radar Data, TU Delft, Delft University of Technology, 2006.

[3].

R. Wang, O. Loffeld, H. Nies, S. Knedlik, M. Hagelen, and H. Essen, “Focus FMCW SAR data using the wavenumber domain algorithm”, IEEE Transactions on Geoscience and Remote Sensing, vol. 48, no. 4, pp. 2109-2118, 2010.

[4].

A. Ribalta, “Time-domain reconstruction algorithms for FMCW-SAR”, IEEE Geoscience and Remote Sensing Letters, vol. 8, no. 3, pp. 396-400, 2011.

[5].

Z. H. Jiang, H. F. Kan, and J. W. Wan, “A chirp transform algorithm for processing squint mode FMCW SAR data”, IEEE Geoscience and Remote Sensing Letters, vol. 4, no. 3, pp. 377-381, 2007.

[6].

Yue Liu, Yun Kai Deng, R. Wang, and O. Loffeld, “Bistatic FMCW SAR signal model and imaging approach”, IEEE Transactions on Aerospace and Electronic Systems, vol. 49, no. 3, pp. 2017-2028, 2013.

[7].

P. Cheng, Q. Xin, J. Wan, and Z. Wang, “Efficient detection of ground moving targets in FMCW SAR by focusing”, IEEE Transactions on Geoscience and Remote Sensing (IGARSS), vol. 53, no. 2, pp. 920-932, 2015.

[8].

A. Meta, P. Hoogeboom, “Signal processing algorithms for FMCW moving target indicator synthetic aperture radar”, in Proc. IGARSS ’05, vol. 1, pp. 316-319, 2005.

[9].

Eric Jacobsen, Peter Kootsookos, “Fast, accurate frequency estimators”, IEEE Signal Processing Magazine, vol. 24, no. 3, pp. 123-125, 2007.

[10].

Ozdemir Caner, Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms, vol. 210, John Wiley & Sons, 2012.

[11].

Soumekh, Mehrdad. Synthetic Aperture Radar Signal Processing, New York: Wiley, 1999.

[12].

Beard, Gavin Spencer, Performance Factors for Airborne Short-Dwell Squinted Radar Sensors, Diss. UCL (University College London), 2011.

Author Information

이 혁 중

jkiees-28-6-459-i1

2013년 2월: 서강대학교 전자공학과 (공학사)
2015년 2월: 한국과학기술원 전기 및 전자공학부 (공학석사)
2015년 2월～현재: 한국과학기술원 전기 및 전자공학부 박사과정
[주 관심분야] Signal Processing for Radar Systems, Detection and Estimation 등

전 주 환

jkiees-28-6-459-i2

1980년 2월: 서강대학교 전자공학과 (공학사)
1984년 2월: Cornell University 전자공학과 (공학석사)
1989년 2월: Stanford University 전자공학과 (공학박사)
1992년 2월～현재: 한국과학기술원 전기 및 전자공학부 교수
[주 관심분야] Signal Processing for Wireless Communication, Signal Processing for Radar Systems, Detection and Estimation 등

송 성 찬

jkiees-28-6-459-i3

2001년 2월: 한국항공대학교 항공전자공학과 (공학사)
2003년 2월: 한국항공대학교 항공전자공학과 (공학석사)
2002년 11월～2015년 6월: 삼성탈레스(주) 전문연구원
2015년 7월～2016년 9월: 한화탈레스(주) 전문연구원
2016년 10월～현재: 한화시스템(주) 수석연구원
[주 관심분야] 레이다 신호처리, 레이다 시스템 등