Ⅰ. 서 론
초기에 레이다에서 수행되던 탐색, 추적, 화기 통제 등의 기능을 단일 레이다로 수행할 수 있는 다기능 레이다(MFR: Multi Function Radar)의 출현으로, 항공기용 레이다는 임무를 신속하고 유동적으로 처리할 수 있게 되었다. 지상이나 함상에 고정된 레이다에 비해 항공기, 특히 전투기 등의 기수에 탑재되는 레이다는 무게나 크기 발열 및 계산 처리에 제약이 비교적 크다. 또한, 공대지, 공대공 등의 다양한 운용모드와 전장의 상황에 따라 유동적이고 효과적으로 대처할 수 있는 자원관리 기법이 필요하게 되었다.
탐색이나 추적 등 특정 기능의 성능을 최적화 하고자 하는 자원관리 알고리듬[1]>~[7]들이 다양하게 제시되어 왔으나, 레이다 모델, 추적 필터, 우선순위 선정 및 레이다 운용 환경을 포함하는 시뮬레이션을 통해 레이다 성능을 분석하려는 시도는 많이 이루어지지 않았다. 참고문헌 [1]에서는 레이다/환경 통합 시뮬레이터 구조를 제시하였으나, 항공기와 표적의 운동모델을 3자유도로 단순화하여 실제 레이다가 운용되는 공대공 교전상황을 정밀하게 모사하지는 않았다. 특히 3자유도 운동 모델의 경우, 항공기의 자세를 고려할 수 없어 레이다 좌표계의 회전이 고려되지 않았다.
항공기의 자세 변화는 추적 성능과 빔 계획 등에 큰 영향을 미치므로 항공기의 자세를 정밀하게 모사하는 것은 레이다/환경 시뮬레이터에서 중요한 요소이다. 단순화된 항공기 경로 및 자세를 생성하는 방법에 대해서는 그래프 탐색(graph search)을 이용해 이산화(discretized)된 항공기의 좌표와 자세를 생성하는 방법[16], 경로점(waypoint)을 직선 형태로 지나는 궤적을 생성해 평활화(smoothing)하여 현실적인 궤적을 생성하는 방법[17] 등 다양한 선행연구가 존재한다. 하지만 이러한 단순화 모델의 경우, 여전히 항공기의 자세를 정밀하게 모사 할 수 없다는 단점이 있다. 본 연구에서는 항공기의 자세를 정밀하게 모사하기 위해 강체 동역학과 공력 모델을 고려한 비행체 6자유도 시뮬레이션 환경을 구성하였다.
아군 항공기의 자세를 정밀하게 모사할 경우, 항공기 기수에 탑재된 레이다의 시야각과 추적 성능이 항공기의 기동에 따라 변하는 것을 보다 정확하게 반영할 수 있다. 적군 항공기의 6자유도 모사는 표적의 급변하는 반사면적(RCS: Radar Cross Section)을 고려한 시뮬레이터로의 확장을 가능하게 한다.
본 연구에서는 항공기 탑재 다기능 레이다의 실제 레이다 시뮬레이션을 위해 레이다 모델링과 추적 필터, 6자유도 동역학 모델에 따른 항공기 자세 및 궤적 생성 방법이 제안되었다. 이를 기반으로 항공기의 자세 변화가 반 영된 레이다/환경 통합 시뮬레이션을 구축하였으며, 시나리오를 생성해 검증하였다.
Ⅱ. 본 론
레이다에서 표적의 탐지 및 측정은 레이다에서 방사된 신호가 표적을 맞고 되돌아온 반송신호강도(SNR: Signal to Noise Ratio)에 따라 결정된다.
SNR S는 표적의 RCS(Radar Cross Section) σ, 표적과 레이다간의 거리 R, 레이다 시스템 손실 Ls등에 따라 결정되는데, 본 연구에서는 표적이 레이다에서 방사된 빔의 중심에서 벗어난 정도 Δϕuv와 레이다 배열 평면의 수직 방향으로부터 표적이 벗어난 정도 ψ에 따른 신호강도의 감소를 고려하여 아래의 식을 사용하였다[1],[8].
여기서 tp는 펄스폭, np는 펄스 개수, 는 peak power, Gt, Gr는 송수신이득, λ는 주파수, k는 Boltzmann 상수, Ts는 시스템 유효 온도, ψ는 스캔 각도, θbw는 빔폭이다.
SNR에 따른 표적의 탐지확률은 표적 RCS의 통계적 모델링에 따라 근사식을 활용하여 계산할 수 있다[9]>~[12]. Swerling 모델의 경우 다음과 같은 식을 사용한다.
where
여기서, Pfa는 false alarm probability, nCPI는 송신빔 내의 총 coherent processing interval의 개수이다.
항공기용 레이다에서 측정하는 표적의 정보는 표적과의 거리, 표적과의 거리방향 속력 그리고 레이다 좌표계에서 정의된 방위각 ϕm 및 고도각 θm이다.
레이다를 기준으로 한 레이다 좌표계(xR, yR, zR)에서 표적과의 거리, 거리방향 속력, 각도는 다음과 같이 계산한다.
표적의 측정치는 실제 값에 백색 Gaussian 잡음을 더하여 생성되는 것으로 가정하였다. 잡음의 분산은 다음과 같이 SNR에 따라 결정된다[13],[14].
– 각도(ϕm,θm) 측정 잡음 분산
– 거리(R) 측정 잡음 분산
– 거리방향 속력(V) 측정 잡음 분산
여기서 kM은 monopulse pattern difference slope, c는 광속, τR는 레이다 시간 분해능, ΔV는 속력 분해능이다.
다기능 레이다에서 표적을 탐지하고 추적하는 일반적인 과정은 그림 1을 통해 확인할 수 있으며, 이에 대해 상세히 설명하면 다음과 같다.
먼저 레이다는 지정 탐색영역에 미리 설정된 빔 격자 상에서 빔의 위치를 바뀌어가며 표적 탐색 임무를 수행한다. 이때 탐색 빔을 주사하는 순서는 사용자가 설정할 수 있으며, 본 연구에서는 무작위 순서로 정해진 순서로 탐색임무를 수행하는 것을 가정하였다. 탐색 중 표적으로 의심되는 플롯이 발견되면, 해당 위치에 빔을 재주사하여 실제 표적인지를 확인한다.
두 차례의 확인 빔을 통해 동일한 플롯이 측정되면, 추적 초기화1와 추적을 순차적으로 수행한다. 여기서 추적 초기화란 표적을 안정적으로 지속 추적하기 위하여 추적 필터를 충분히 수렴시키는 과정을 말하며, 추적과 기능은 동일하지만 빠른 주기로 임무를 수행한다는 점에서 차이가 있다[6]. 추적 초기화 1 과정에서 표적 탐지에 실패하였을 시, 추적 초기화 2를 통해 표적의 예상 위치 주변에 복수의 빔을 주사하여 추적 초기화를 재개한다.
추적 필터는 추적 초기화 단계부터 사용하며, 표적의 추정 정보를 활용하여 각도상의 표적 예상 이동 위치에 다음번 추적 빔을 주사하게 된다. 본 연구에서 표적의 상태 추적을 위한 추적 필터로는 등속운동 모델을 이용하는 EKF(Extended Kalman Filter)[13],[14]를 사용하였다.
재탐색/추적관리는 추적 임무 수행 중 표적을 놓치게 되었을 때, 추적 초기화 2와 마찬가지로 표적의 예상 위치와 그 주변에 복수의 빔을 주사하여 표적을 재획득하는 기능이다.
그림 2는 본 연구에서 구성한 다기능 레이다 시뮬레이터의 구조를 나타낸 것이다.
시뮬레이션이 시작되면, 미리 설정된 시뮬레이션 파라미터들이 입력된다. 시뮬레이션 파라미터는 레이다 특성치와 표적 생성 시나리오 및 궤적 정보로 구성되어 있으며, 각 임무에 해당하는 파형별 기준 SNR과 해당 거리, dwell time, 빔 폭, 거리 분해능, PRF 등을 포함한다. 파라미터가 입력되면 레이다의 운용을 위해 탐색 빔들로 이 루어진 임무 집합이 생성된다.
레이다의 기능 전환은 레이다 시뮬레이터 전체 구조 중에 임무 관리자 모듈(Task manager)에서 수행하게 된다. 임무 관리자에서는 레이다에서 수행할 다음 임무뿐만 아니라, 요구되는 수행 시점을 정하게 된다.
이후 스케줄러(Scheduler)에서 시간 순서대로 가장 먼저 준비된 빔에 임무를 할당하여 차례대로 임무를 수행한다. 하나의 임무가 실행되면 레이다/환경 시뮬레이션 모듈에서 빔의 위치와 빔 파라미터 및 표적의 위치에 따라 신호강도와 탐지확률을 계산하고, 난수를 생성하여 탐지 여부를 결정한다.
Pilot 모듈은 조종사가 레이다의 운용모드를 설정하거나, 특정 관심 영역 지정 및 표적의 우선순위를 조정하는 모듈이다.
항공기 궤적 생성은 아군 항공기의 위치와 자세를 생성함으로써 레이다 좌표계를 정의하고, 공대공 교전 상황에서의 표적모델로 사용되는 적군 항공기의 좌표와 자세를 생성하는 과정이다.
6자유도 강체 동역학을 고려하여 시뮬레이션 환경을 구축하면 항공기의 자세를 정밀하게 모사할 수 있으며, 이에 따라, 항공기 자세 변화에 따른 레이다 좌표계의 변화가 정밀하게 고려될 수 있다. 마찬가지로 표적으로 사용되는 적군 항공기의 자세가 정밀하게 고려되기 때문에 레이다 반사면(radar cross section)을 고려한 레이다 모델링으로의 확장이 용이하다.
본 연구에서는 항공기를 질량이 변하지 않는 강체로 가정하여 모델링하였으며, 항공기의 제어를 위한 제어 입력으로는 추력(T), 에일러론 각(δail), 엘리베이터 각(δele), 러더 각(δrud)이 있다고 가정하였다.
지구의 북쪽, 동쪽, 아래쪽을 기준으로 하는 NED 좌표계와 항공기 기체의 동체 기수축, 오른쪽 날개 방향, 그리고 동체 아랫 방향을 기준으로 하는 기체고정 좌표계(body frame coordinate)는 그림 3과 같이 정의된다.
정의된 기체고정 좌표계에서의 각 축 방향 힘과 모멘트를 X,Y,Z,L,M,N, 각 축 방향 속도 및 각속도를 U,V,W,P,Q,R이라고 하면 뉴턴-오일러 방정식과 좌표계 회전변환으로부터 식 (8)~(10)이 도출된다.

항공기의 각방향 힘과 모멘트 값인 X,Y,Z,L,M,N은 중력, 공력, 항력에 의해 생성된다. 항공기에 작용하는 중력은 D 방향으로 작용하며, 일정한 값이다. 공력과 항력은 항공기의 속력(Vt), 받음각(α), 옆 미끄러짐 각(β), 고도(h) 등을 포함하는 운동 상태 값과, 제어 입력에 따라 알려져 있는 표로부터 읽어와 내삽(interpolation)하여 구할 수 있다. 본 연구에서는 항공기의 질량, 관성모멘트, 공력모델, 항력모델 등이 잘 알려져 있는 F-16 항공기의 데이터[18]를 사용하였다. 항공기의 각 축 방향 힘과 모멘트 값을 계산하고 위의 식을 적용하면, 시간에 따른 항공기의 좌표와 자세를 얻을 수 있다.
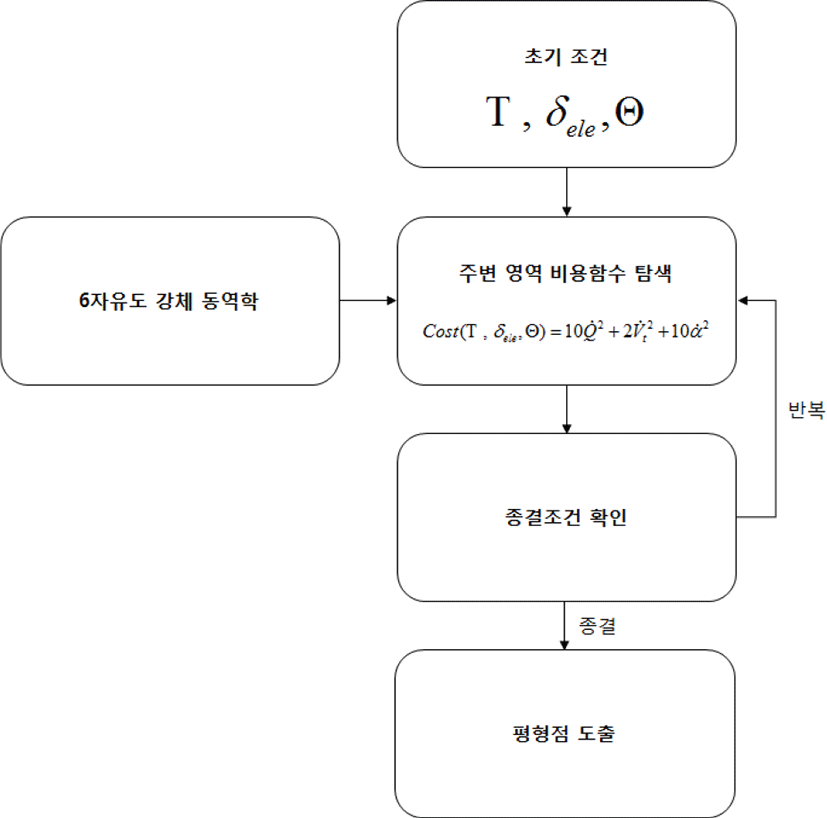
6자유도 강체 동역학 시뮬레이션 모델을 기반으로 항공기의 궤적을 생성하기 위해서는 시뮬레이션 과정에서 항공기의 초기조건을 적절하게 설정해 주어야 한다. 항공기 궤적 생성에서 초기조건은 항공기의 평형 상태(정상 비행 상태, steady state flight)로 설정하였다. 정상 비행 상태는 항공기 기체고정 좌표계에서의 힘과 모멘트가 0 또는 상수가 되도록 하는 특수한 비행 상태이며, 이때 항공기의 상태 및 제어 입력을 평형점(equilibrium point, trim point)이라고 한다. 특히 정상 비행 상태 중, 인 경우에, 항공기는 자세와 고도를 유지하며 일정한 속도로 직선 비행하게 되고, 이러한 비행 상태를 정상 수평 비행(steady level flight) 상태라고 한다. 또한, 항공기기가 자세와 고도를 유지하며, 일정한 각속도로 선회하는 기동을 하는 경우는 로 나타나는 특수한 정상 상태 비행을 의미하며, 이러한 비행 상태를 정상 선회 비행(steady turning flight)이라고 한다. 본 연구에서 항공기의 궤적 생성을 위한 초기 조건으로 항공기의 정상 수평비행 또는 항공기의 정상 선회 비행 상태를 사용하였다.
정상 수평 비행 평형점을 찾는 문제는 항공기가 주어진 고도와 속력 조건으로 직선 비행할 수 있도록 하는 항공기의 자세 상태와, 제어 입력 값들을 찾는 문제로 생각할 수 있다. 이 문제는 항공기의 대칭성에 의해 주어진 고도와 속력 조건에서 을 만족하도록 하는 T,Θ,δele를 찾는 문제로 단순하게 변형된다.
본 연구의 6자유도 강체 동역학 환경에서는 항공기의 각 축 방향 힘과 모멘트가 항공기의 상태에 따른 데이터 표에서 계산되기 때문에 정상 수평 비행 평형점은 수치적으로 풀이 되어야 한다. 정상 수평 비행 평형점을 찾기 위해, 본 연구에서는 비제약조건 다변수함수를 정의하여 비용함수(cost)라고 명명하였다.
비용함수는 T,Θ,δele 값에 의해 결정되며, 정상 수평 비행 상태인 에서는 0의 값을 갖게 된다. 또한, 정상 수평 비행 상태가 아닐 때, 비용함수는 양수 값을 갖게 된다. 이러한 함수의 특성에 따라, 항공기가 주어진 고도, 속력 조건에서 정상 수평 비행이 가능하다면, 정상 비행 상태를 만족하는 T,Θ,δele 조건에서 비용함수가 최솟값을 갖게 된다. 본 연구에서는 비제약조건 다변수 함수의 최솟값을 찾기 위해 사용되는 Nelder-Mead simplex direct search 알고리즘을 적용하여 항공기의 정상 수평 비행 평형점 수치해를 찾도록 하였다.
정상 선회 비행 상태 평형점을 찾는 문제는 정상 수평 비행 상태 문제와 유사하게 풀이 되었다. 항공기가 주어진 각속도로 일정하게 선회하는 방법은 유일하지 않으므로 문제를 풀기 위해 항공기가 coordinate turn으로 회전함이 가정되었다. 이에 따라 항공기의 정상 수평 비행 평형점 탐색 문제는 주어진 고도, 속력, 선회 속도 조건에 대 해서 를 만족하도록 하는 항공기의 상태 및 제어 입력 값 ϕ,θ,Vt,α,P,Q,R,T,δail,δele,δrud를 찾는 문제로 변형되며, 이후 정상 수평 비행 상태 평형점을 찾는 것과 같은 방법을 활용해 정상 선회 비행 평형점을 찾을 수 있다.
항공기의 궤적을 실제 비행 상황과 유사하게 모사하기 위해서는 제어 입력이 실제 항공기에서 입력 가능한 형태로 주어져야 한다. 본 절에서는 항공기 궤적 생성 과정에서 가정한 항공기의 제어 입력 구동기(actuator) 모델에 대한 내용을 다룬다.
실제 항공기의 구동기를 정밀하게 시뮬레이션 환경에 구현할 경우, 계산의 비효율성을 초래할 수 있으므로, 본 연구에서는 단순화된 구동기 모델을 사용하였다. 엔진의 경우 1,000 lbf~19,000 lbf의 범위 내의 추력만 낼 수 있도록 하였으며, 그 변화율을 최대 10,000 lbf/sec로 제한하고, 시상수(time constant)가 1초인 1차 지연 모델 구동기를 설정하였다. 에일러론, 엘리베이터, 러더를 포함하는 제어 면 구동기의 경우, 제어면의 각도와 그 변화율에 제한을 둔 1차 지연 모델로 설정하였다. 각 제어면의 제한값은 표 1과 같다.
| 최대 값 | 최대 변화율 | 시상수 | |
|---|---|---|---|
| δele | ±25.0° | ±60.0°/sec | 0.0495 sec |
| δail | ±21.5° | ±80-0°/sec | 0.0495 sec |
| δrud | ±30-0° | ±l20-0°/sec | 0.0495 sec |
항공기 오토파일럿 설계는 항공기가 원하는 비행상태를 유지하거나, 현재 상태에서 다른 비행상태로 변경하기 위해 사용될 제어 입력 값을 결정하는 문제이다. 즉, 원하는 기동을 하는 항공기의 궤적을 생성하기 위해 6자유도 시뮬레이션 환경에 사용되는 제어 입력을 올바르게 설정하기 위한 제어기를 설계하는 과정이다.
항공기의 동역학 모델은 항공기의 속력, 자세, 제어 입력에 따라 공력 값이 크게 변하기 때문에 비선형성이 크다고 할 수 있다. 따라서 항공기의 제어기 설계에 일반적인 선형 제어 이론을 적용하기 위해 항공기 동역학 모델을 선형화 하는 작업이 선행되었다. 항공기 동역학 모델 선형화는 항공기의 평형점을 기준으로 수행할 수 있으며, 항공기의 고도, 속력, 선회 속도에 따라 얻은 평형점 표로부터 평형점에서의 항공기의 상태 및 자세와 제어 입력
값을 얻어 항공기 동역학 모델 선형화가 진행되었다[19]. 항공기 동역학 모델을 선형화 하면 , y= Cx+Du 형태로 표현되는 상태 공간 표현식(state space form) 선형 모델을 얻을 수 있다. 해당 선형 모델을 사용하여, 선형 제어에서 일반적으로 사용되는 Linear Quadratic Regulator(LQR)[20] 제어기를 설계하였다.
항공기는 자세와 제어 입력 값이 동일하다고 하더라도 고도에 따른 공기 밀도에 변화에 의해 항공기의 동역학적 특성이 크게 변하는 특징이 있다. 따라서 항공기를 올바르게 제어하기 위해 항공기의 비행 특성에 따라 서로 다른 제어기를 설계해야 하며, 본 연구에서는 항공기 제어기 설계에 일반적으로 사용되는 게인 스케줄링(gain scheduling) 기법이 적용되었다. 본 연구에서는 항공기의 속력, 고도에 따라 제어기에 사용되는 되먹임 이득(feedback gain) 값을 다르게 설정하여 항공기가 모든 비행 가능 영역에서 올바르게 제어될 수 있도록 구현하였다.
항공기 유도 명령 생성은 주어진 시나리오에 따라 항공기가 적절한 방향, 속도, 고도로 비행하도록 하는 것이다. 본 연구에서는 크게 두 가지 시나리오를 구현할 수 있도록 항공기의 유도 명령이 설계되었다. 첫 번째는 시 간에 따라 항공기의 기동 상태(고도, 비행 방향, 자세)를 사용자가 설정할 수 있도록 한 시나리오이며, 두 번째 는 항공기의 경로점 추종(waypoint tracking) 시나리오 이다.
항공기의 제어기가 이미 설계되어 있기 때문에, 항공기의 기동 상태를 설정하는 유도 명령은 직관적으로 구현된다. 항공기의 경로점 추종 시나리오의 경우, 경로점의 좌표로부터 고도 명령을 얻고, 경로점과 항공기 간의 기하학적 관계로부터 항공기의 비행 방향을 설정하는 형태로 구현되었다.
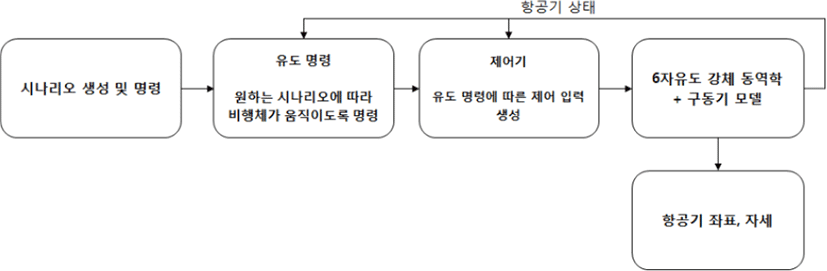
항공기의 동역학 모델, 구동기 모델, 제어기(오토파일럿), 유도명령 설계가 완료되어 그림 6과 같이 항공기의 비행 시나리오를 설정하고, 시뮬레이션을 진행하여 시간에 따른 항공기의 좌표와 자세를 쉽게 얻을 수 있도록 구현하였다.
표 2에 제시되어 있는 시나리오에 따라 북쪽 방향으로 초기 기동하고 있는 항공기가 경로점을 추종하도록 한 궤적 생성 결과는 그림 7과 같다.
| 북(ft) | 동(ft) | 고도(ft) | 속력(ft/s) | |
|---|---|---|---|---|
| 초기 조건 | 0 | 0 | 11,000 | 610 |
| 경로점 1 | 40,000 | 45,000 | 13,000 | 650 ft/s 유지 |
| 경로점 2 | 120,000 | 70,000 | 15,000 | |
| 경로점 3 | 250,000 | 60,000 | 20,000 | |
| 경로점 4 | 500,000 | 0 | 10.000 |
이 때 최초 항공기가 북쪽 방향으로 정상 수평 비행하는 순간, 동쪽 방향으로 선회하는 순간, 그리고 고도를 상승 및 하강하며 기동하는 순간의 자세를 가시화한 결과는 그림 8과 같다.
항공기가 선회하는 과정에서 횡전(rolling) 하며 고도를 변경하는 과정에서 기수를 들고, 내리는 등 실제 항공기의 동역학적 특성을 반영한 자세를 유지하며 기동하는 것을 확인할 수 있다.
Ⅲ. 시뮬레이션
본 연구에서 개발한 레이다/환경 통합 시뮬레이터의 정상 작동을 검증하기 위해 공대공 항공기 운용상황에서의 특정 시나리오를 구성하였다.
레이다의 탐색영역은 좌우 −30°~30°, 빔폭 4°×4° 기준 4개의 bar로 설정하였다. 탐색 패턴의 경우, 탐색영역 내에서 원형 빔을 삼각형 격자 형태로 생성하였다[5]. 레이다의 성능은 표적의 레이다 배열 평면 수직방향에 정확히 위치하였을 때 약 70 km의 상대거리에서 안정적인 추적이 가능하도록 설정하였으며, 최대 20개의 표적 추적이 가능하다. 표적의 RCS는 SwerlingⅢ type을 가정하였으며, 0.8~1.2 m2에서 임의의 값을 생성하여 사용하였다.
2-2절에 기술된 항공기 6자유도 강체 동역학 모델을 기반으로 항공기의 기동을 생성하였다. 항공기의 다양한 자세 기동이 포함된 전장 상황을 모사하기 위해 아군 항공기는 고도를 증가시키며 북쪽에서 동쪽으로 기수를 트는 기동을 하는 시나리오를 구성하였으며, 레이다 표적으로 사용되는 적군 항공기는 고도를 변화시키며 직선 및 선회 비행하며 다양한 방향으로 기동하는 형태로 구성하 였다.
시뮬레이션에 사용된 항공기의 초기 상태와 항공기의 기동 시나리오는 저고도에서 빠른 속력으로 비행하는 항공기의 비행 상태를 모사하였으며, 표 3, 4에 나타나 있다.
아군 항공기와 5대의 적군 항공기의 궤적을 생성한 결과는 그림 9와 같다. 얻은 적군 항공기의 궤적은 아군 항공기의 기체 고정 좌표계를 기준으로 변환되어, 레이다 시뮬레이션에서 표적 좌표로 사용된다.
본 절에서 시뮬레이션을 위해 사용한 레이다 임무 스케줄러는 WMDD(Weighted Modified Due Date)[15]이다. WMDD는 임무 처리 지연시간의 가중합을 최소화하는 문제에 적용하기 위해 개발된 휴리스틱 기법이며, 본 시뮬레이션에서는 추적 관리/재탐색, 표적 확인, 추적 초기화, 추적, 탐색 순서로 기능 간 우선순위를 설정하였다.
그림 10은 레이다 UV 평면상에서 레이다 표적간 실제 궤적 및 추적 필터로부터의 추정 결과를 나타낸 것이다. 항공기와 표적이 기동함에 따라 매우 복잡한 형태의 상대 운동이 이루어짐을 확인할 수 있으며, 미리 지정된 영역에서의 탐색임무에서 표적 탐지에 성공하고, 이후 지속적으로 추적에 성공하는 것을 확인할 수 있다.
그림 11은 레이다 기준(항공기 기체 고정 좌표)의 xyz 좌표계 상에서의 상대 위치 및 추정 결과를 나타낸다.
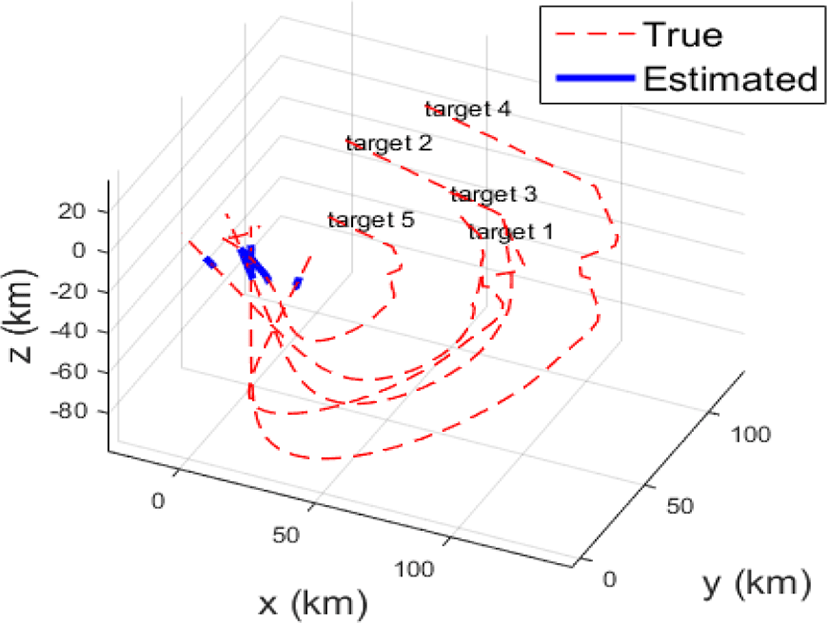
그림 12는 표적별 반송신호강도 변화와 탐지확률 변화를 나타낸다. 레이다는 표 4에서 설명한 선회 기동을 하는 표적 5를 가장 빨리 탐지에 성공하며, 이후 표적 5가 레이다 시야에서 벗어남에 따라 약 150초 부분에서 표적을 놓치는 것을 확인할 수 있다. 나머지 표적들은 약 220초부터 순차적으로 탐지되며, 추적이 지속되다가 레이다 탐지 반경에서 벗어난 것으로 나타난다.
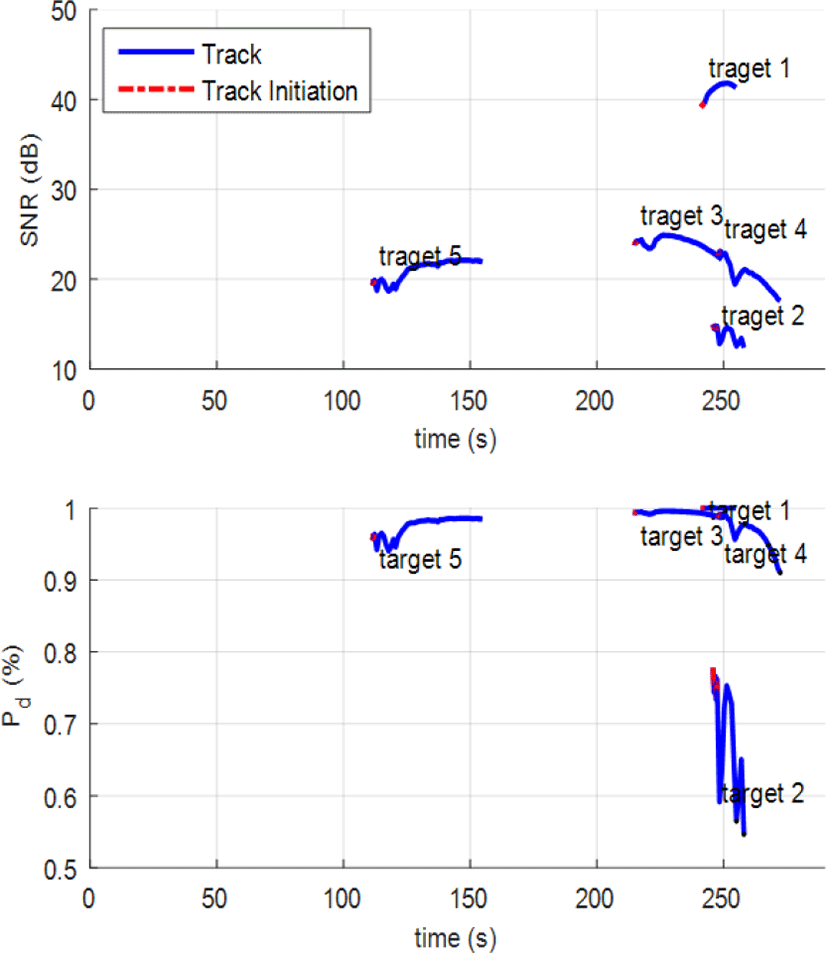
그림 13은 표적의 추정 오차를 나타낸 것이다. 레이다가 표적에 대해 추적 임무를 수행하는 시점에서는 표적들이 항공기로부터 상대적으로 근거리에서 기동하기 때문에 안정적인 추적이 이루어짐을 확인할 수 있다.
이와 같이 주어진 시나리오에서 6자유도 강체 동역학 모델을 기반으로 아군 및 적군 항공기 자세 및 궤적 생성을 한 뒤 아군 항공기 기체 고정 좌표계로 변환하여 표적의 레이다 좌표를 생성하고, 표적을 탐지, 추적하는 등의 일련의 과정이 정상적으로 이루어는 것을 확인할 수 있으며, 구현된 통합 시뮬레이터 상에서 레이다 추적 성능 분석이 가능하다는 것을 확인하였다.
Ⅳ. 결 론
본 논문에서는 6자유도 강체 동역학 모델을 고려하여 항공기의 궤적과 자세를 생성함으로써, 공대공 교전상황에서의 레이다 운용 환경을 정밀하게 모사하였다. 또한, 레이다 운영환경을 표적과 항공기의 상대운동에 의한 표적 반송 신호 강도에 따른 탐지확률 및 측정치 생성 모델링이 수행되었으며, 추적 필터와 통합해 레이다/환경 통합 시뮬레이터를 구성하였다.
구현된 시뮬레이터를 검증하기 위해 공대공 시나리오를 구성하였으며, 시뮬레이션을 통해 실제 레이다 운용상황이 올바르게 구현되었음을 확인하였다.
본 논문에서 구성한 레이다/환경 통합 시뮬레이터는 추후 자원관리 모듈 통합 및 표적의 RCS 변화 고려, 그리고 항공기 항법 통합이 가능할 것으로 판단된다. 또한, 향후 개발될 자원관리 기법의 성능 평가를 위한 도구로서 활용될 수 있을 것으로 기대한다.















